Chapter 1 Introduction to Research and Data
1.2 Data Analysis or Statistics?
This textbook provides an introduction to data analysis, and should not be confused with a statistics textbook. Technically, it is not possible to separate data analysis from statistics, as statistics is a field of study that emerged specifically for the purpose of providing techniques for analyzing data. In fact, with the exception of this chapter, most of the material in this book addresses the use of statistical methods to analyze political and social outcomes; but that is different from a focus on statistics for the sake of learning statistics. Most straight-up texts on statistics highlight the sometimes abstract, mathematical foundations of statistical techniques, with less emphasis on concrete applications. This textbook, along with most undergraduate books on data analysis, focuses much more on concrete applications of statistical methods that facilitate the analysis of political and social outcomes. Some students may be breathing a sigh of relief, thinking, “Oh good, there’s no math or formulas!” Not quite. The truth of the matter is that while a lot of the math underlying the statistical techniques can be intimidating and off-putting to people with a certain level of math anxiety (including the author of this book!), some of the key formulas for calculating statistics are very intuitive, and taking time to focus on them (even at a surface level) helps students gain a solid understanding of how to interpret statistical findings. So, while there is not much math in the pages that follow, there are statistical formulas, sometimes with funny-looking Greek letters. The main purpose of presenting formulas, though, is to facilitate understanding and to make statistics more meaningful to the reader. If you can add, subtract, divide, multiply, and follow instructions, the “math” in this book should not present a problem.
1.3 Research Process
Though the emphasis in this book is on data analysis, that is just one important part of the broader research enterprise. In fact, data analysis on its own is not very meaningful. Instead, for data analysis to produce meaningful and relevant results, it must take place in the context of a set of expectations and be based on a host of decisions related to those expectations. When framed appropriately, data analysis can be used to address important social and political issues.
Social science research can be thought of as a process. As a process, there is a beginning and an end, although it is also possible to imagine the process as cyclical and ongoing. What is presented below is an idealized version of the research process. There are a couple of important things to understand about this description. First, this process is laid out in four very broadly defined categories for ease of understanding. The text elaborates on a lot of important details that should not be skipped. Second, in the real world of the research there can be a bit of jumping around from one part of the process to another, not always in the order shown below. Finally, this is just one of many different ways of describing the research process. In fact, if you consult ten different books on research methods in the social sciences, you will probably find ten somewhat different depictions of the research process. Having said this, though, at least in points of emphasis, all ten depictions should have a lot in common. The major parts of this process are presented in Figure 1.1.
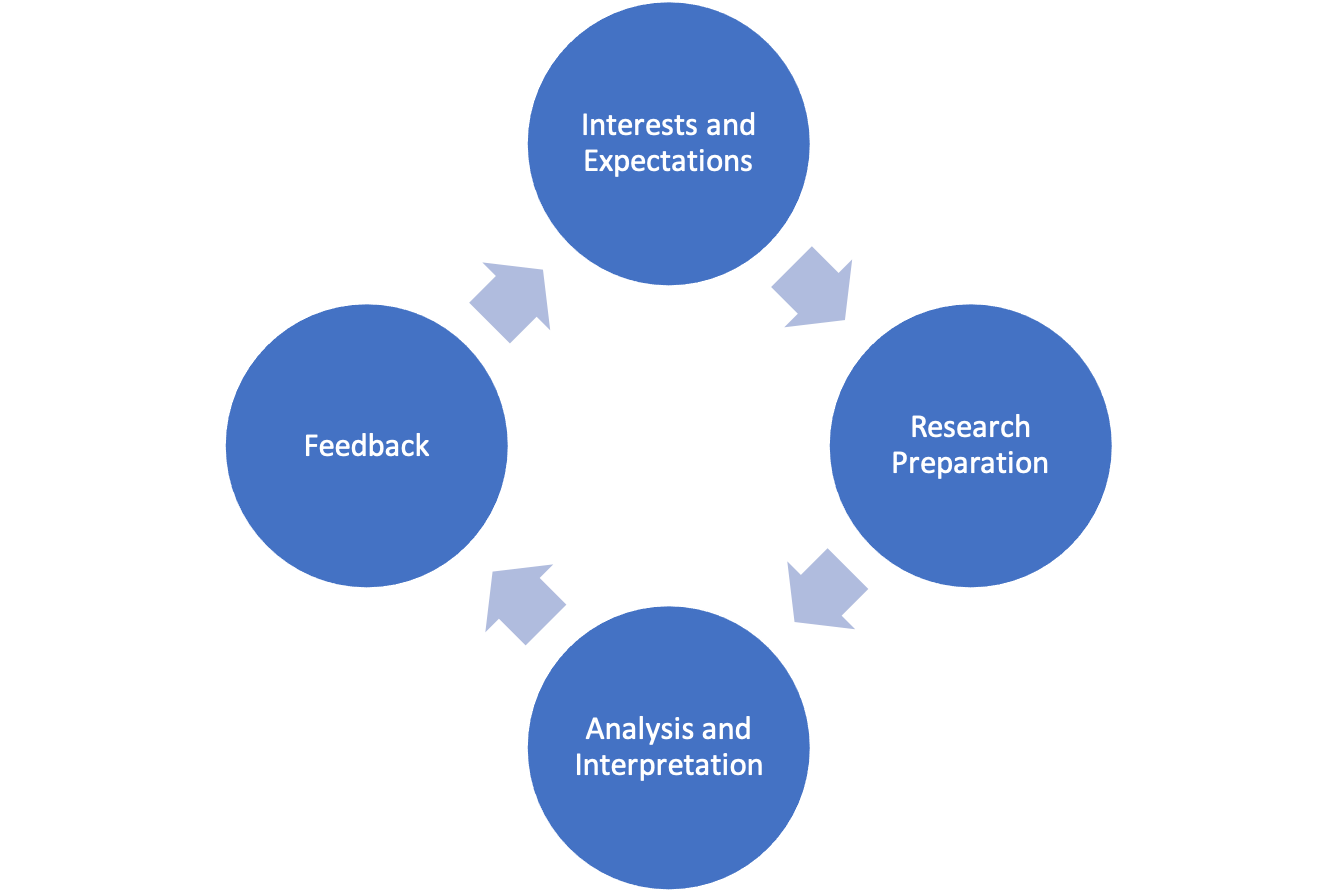
Figure 1.1: An Idealized Description of the Research Process
1.3.1 Interests and Expectations
The foundation of the research process is research interests or research ideas. College students are frequently asked to write research papers and one of the first parts of the writing assignment is to identify their research interests or, if they are a bit farther along, their research topic. This can be a very difficult step in the process, especially if the students are told to find a research topic as part of an assignment, rather than independently deciding to do a research paper because of something that interests them. Frequently, students start with something very broad, perhaps, “I want to study elections,” or something along the lines of “LGBTQ rights.” This is good to know, but it is still too overly general to be very helpful. What is it about elections or LGBTQ rights that you want to know? There are countless interesting topics that could be pursued in either of these general categories. The key to really kicking things off is to narrow the focus to a more useful research question. Maybe a student interested in elections has observed that some presidents are re-elected more easily than others and settles on a more manageable goal, explaining the determinants of incumbent success in presidential elections. Maybe the student interested in LGBTQ rights has observed that some states offer several legal protections for LGBTQ residents, while other states do not. In this case, the student might limit their research interest to explaining variation in LGBTQ rights across the fifty states. The key here is to move from a broad subject area to a narrower research question that gives some direction to the rest of the process.
Still, even if a researcher has narrowed their research interest to a more manageable topic, they need to do a bit more thinking before they can really get started; they need a set of expectations to guide their research. In the case of studying sources of incumbent success, for instance, it is still not clear where to begin. Students need to think about their expectations. What are some ideas about the things that might be related to incumbent success? Do these ideas make sense? Are they reasonable expectations? What theory is guiding your research?
“Theory” is one of those terms whose meaning we all understand at some level and perhaps even use in everyday conversations (e.g., “My theory is that…”), but it has a fairly specific meaning in the research process. In this context, theory refers to a set of logically connected propositions (or ideas/statements/assumptions) that we take to be true and that, together, can be used to explain a given phenomenon (outcome) or set of phenomena (outcomes). Think of a theory as a rationale for testing ideas about the things that you think explain the outcome that interests you. Another way to think of a theory in this context is as a model that identifies how things are connected to produce certain outcomes.
A good theory has a number of characteristics, the most important of which are that it must be testable, plausible, and accessible. To be testable, it must be possible to subject the theory to empirical evidence. Most importantly, it must be possible to show that the theory does not provide a good account of reality, if that is the case; in other words, the theory must be falsifiable. Plausibility comes down to the simple question of, on its face, given what we know about the subject at hand, does the theory make sense? If you know something about the subject matter and find yourself thinking “Really? This sounds a bit far-fetched,” this could be a sign of a not-very-useful theory. Finally, a good theory needs to be understandable, easy to communicate. This is best accomplished by being parsimonious (concise, to the point, as few moving parts as possible), and by using as little specialized, technical jargon as possible.
As an example, a theory of retrospective voting can be used to explain support and opposition to incumbent presidents. The retrospective model was developed in part in reaction to findings from political science research that showed that U.S. voters did not know or care very much about ideological issues and, hence, could not be considered “issue voters.” Political scientist Morris Fiorina’s work on retrospective voting countered that voters don’t have to know a lot about issues or candidate positions on issues to be issue voters.4 Instead, he argued that the standard view of issue voting is too narrow and a theory based retrospective issues does a better job of describing the American voter. Some of the key tenets of the retrospective model are:
Elections are referendums on the performance of the incumbent president and their party;
Voters don’t need to understand or care about the nuances of foreign and domestic policies of the incumbent president to hold their administration accountable;
Voters only need to be aware of the results of the those policies, i.e, have a sense of whether things have gone well on the international (war, trade, crises, etc.) and domestic (economy, crimes, scandals, etc.) fronts;
When times are good, voters are inclined to support the incumbent party; when times are bad, they are less likely to support the incumbent party.
This is an explicitly reward-punishment model. It is referred to as retrospective voting because the emphasis is on looking back on how things have turned out under the incumbent administration rather than comparing details of policy platforms to decide if the incumbent or challenging party has the best plans for the future.
The next step in this part of the research process is developing hypotheses that logically flow from the theory. A hypothesis is speculation about the state of the world. Research hypotheses are based on theories and usually assert that variations in one variable are associated with, result in, or cause variation in another variable. Typically, hypotheses specify an independent variable and a dependent variable. Independent (explanatory) variables, often represented as X, are best thought of as the variables that influence, or shape outcomes in other variables. They are referred to as independent because we are not assuming that their outcomes depend on the values of other variables. Dependent (response) variables, often represented as Y, measure the thing we want to explain. These are the variables that we think are affected by the independent variables. One short-cut to recalling this is to remember that the outcome of the dependent variable depends upon the outcome of the independent variable.
Based on the theory of retrospective voting, for instance, it is reasonable to hypothesize that economic prosperity is positively related to the level of popular support for the incumbent president and their party. Support for the president should be higher when the economy is doing well than when it is not doing well. In social science research, hypotheses sometimes are set off and highlighted separately from the text, just so it is clear what they are:
H1: Economic prosperity is positively related to the level of popular support for the incumbent president and their party. Support for the president should be higher when the economy is doing well than when it is not doing well.
In this hypothesis, the independent and dependent variables are represented by two important concepts, economic prosperity and support for the incumbent president, respectively. Concepts are abstract ideas that help to summarize and organize reality; they define theoretically relevant phenomena and help us understand the meaning of the theory a bit more clearly. But while concepts such as these help us understand the expectations embedded in the hypothesis, they are sufficiently broad and abstract that we are not quite ready to analyze the data.
1.3.2 Research Preparation
In this stage of the research process, a number of important decisions need to be made regarding the measurement of key concepts, the types of data that will be used, and how the data will be obtained. The hypothesis developed above asserts that two concepts–economic prosperity and support for the incumbent president–are related to each other. When you hear or read the names of these concepts, you probably generate a mental image that helps you understand what they mean. However, they are still a bit too abstract to be useful from a measurement perspective. What we need to do is move from abstract concepts to operational variables–concrete, tangible, measurable representations of the concepts. How are these concepts going to be represented when doing the research? There are a number of ways to think about measuring these concepts (see Table 1.2). If we take “economic prosperity” to mean something like how well the economy is doing, we might decide to use some broad-based measure, such as percentage change in the gross domestic product (GDP) or percentage change in personal income, or perhaps the unemployment rate at the national level. We could also opt for a measure of perceptions of the state of the economy, relying on survey questions that ask individuals to evaluate the state of the economy, and there are probably many other ways you can think of to measure economic prosperity. Even after deciding which measure or measures to use, there are still decisions to be made. For instance, let’s assume we decide to use change in GPD as a measure of prosperity. We still need to decide over what time period we need to measure change. GDP growth since the beginning of the presidential term? Over the past year? The most recent quarter? It’s possible to make good arguments for any of these choices.
| Concept | Operational Variables |
|---|---|
| Economic Prosperity | GDP change, income change, economic perceptions, unemployment, etc. |
| Incumbent Support | Approval rating, election results, congressional elections, etc. |
The same decisions have to be made regarding a measure of incumbent support. In this case, we might use polling data on presidential approval, presidential election results, or perhaps support for the president’s party in congressional elections. The point is that before you can begin gathering relevant data, you need to know how the key variables are being measured. In the example used here, it doesn’t require much effort to figure out how to operationalize the concepts that come from the hypotheses. This is not always the case. Some concepts are much more difficult to operationalize–that is, to measure–than others. Think about these concepts, for instance: power, justice, equality, fairness. Concepts such as these are likely to present more problems for researchers than concepts like economic prosperity and/or support for the incumbent president.
There are two very important concerns at the operationalization stage: Validity and Reliability. The primary concern with validity is to make sure you are measuring what you think you are measuring. You need to make sure that the operational variables are good representations of the concepts. It’s tough to be certain of this, but one important, albeit imprecise, way to assess the validity of a measure is through its face validity. By this we mean, on its face, does this operational variable make sense as a measure of the underlying concept? If you have to work hard to convince yourself and others that you have a valid measure, then you probably don’t.
Let’s consider the a couple of proposed indicators of support for the incumbent president: presidential approval and election results. Presidential approval is based on responses to survey questions that ask if respondents approve or disapprove of the way the president is handling their job, and election results are, of course, an official forum for registering support for the president (relative to their challenger) at the ballot box. No face validity problem here. On the other hand, suppose a researcher proposes using the size of crowds at campaign rallies or the ratio of positive-to-negative letters to the editor in major newspapers as evidence of presidential support. These are things that might bear some connection to popular support for the president, but are easily manipulated by campaigns, parties, and special interests. In short, these measures have a problem with face validity.
For reliability, the concern is that the measure you are using is consistent. Here the question is whether you would get the same (or nearly the same) results if you measured the concept at different points in time, or across different (but similarly drawn) samples. So, for instance, in the case of measuring presidential approval, you would expect that outcomes of polls used do not vary widely from day to day and that most polls taken at a given point in time would produce similar results.
Data Gathering. Once a researcher has determined how they intend to measure the key concepts, they must find the data. Sometimes, a researcher might find that someone else has already gathered the relevant data they can use for their project. For instance, researchers frequently rely upon regularly occurring, large-scale surveys of public opinion that have been gathered for extended periods of time, such as the American National Election Study (ANES), the General Social Survey (GSS), or the Cooperative Election Study (CES). These surveys are based on large, scientifically drawn samples and include hundreds of questions on topics of interest to social scientists. Using data sources such as these is referred to as secondary data analysis. Similarly, even when researchers are putting together their own data set, they frequently use secondary data. For instance, to test the hypotheses discussed above, a researcher may want to track election results and some measure of economic activity, economic growth. These data do not magically appear. Instead, the researcher has to put on their thinking cap and figure out where they can find sources for these data. As it happens, election results can be found at David Leip’s Election Atlas (https://uselectionatlas.org), and the economic data can be found at the Federal Reserve Economic Data website (https://fred.stlouisfed.org) and other government sites, though it takes a bit of poking around to actually find the right information.
Even after figuring out where to get their data, researchers still have several important decisions to make. Sticking with the retrospective voting hypothesis, if the focus is on national outcomes of U.S. presidential elections, there are a number of questions that need to be answered. In what time period are we interested? All elections? Post-WWII elections? How shall incumbent support be measured? Incumbent party percent of the total vote or percent of the two-party vote? If using the growth rate in GDP, over what period of time? Researchers need to think about these types of questions before gathering data.
In this book, we will rely on several data sources: a 50-state data set, a county-level political and demographic data set, a cross-national political and socioeconomic data set, and the American National Election Study (ANES), a large-scale public opinion survey conducted before and after the 2020 U.S. presidential election.
1.3.3 Data Analysis and Interpretation
Assuming a researcher has gathered appropriate data for testing their hypotheses and that the data have been coded in such a way that they are suitable to the task (more on this in the next chapter), the researcher can now subject the hypothesis to empirical scrutiny. By this, I mean that they can compare the state of the world as suggested by the hypothesis to the actual state of the world, as represented by the data gathered by the researcher. Generally, to the extent that the relationship between variables stated in the hypothesis looks like the relationship between the operational variables in the real world, then there is support for the hypothesis. If there is a significant disconnect between expectations from the hypothesis and the findings in the data, then there is less support for the hypothesis. Hypothesis testing is a lot more complicated than this, as you will see in later chapters, but for now let’s just think about it as comparing the hypothetical expectations to patterns in data.
Data analysis can take many different forms, and the specific statistics and techniques a researcher uses are constrained by the nature of the data and the expectations from the hypotheses. For example, if the retrospective voting hypothesis is tested using the GDP growth rate to predict the incumbent share of the national popular vote in the post-WWII era, then we would probably use a combination of several techniques: scatter plots, correlations, and Ordinary Least Squares Regression (all to be presented in great detail in subsequent chapters). On the other hand, if the hypothesis is being tested using a national public opinion survey from the 2020 election, then the data would dictate that different methods be used. Assuming the survey asks how the respondents voted, as well as their perceptions of the state of the economy (Getting better, getting worse, or no change over the last year), the analysis would probably rely upon contingency tables, mosaic plots, and measures of association (also covered in subsequent chapters).
Regardless of the type of data or method used, researchers are typically interested in two things, the strength of the relationship and the level of confidence in the findings. By “strength of the relationship” we mean how closely outcomes on the dependent and independent variables track with each other. For instance, if there is a clear and consistent tendency for incumbent presidents to do better in elections when the economy is doing well than when it is in a slump, then the relationship is probably pretty strong. If there is slight tendency for incumbent presidents to do better in elections when the economy is doing well than when it is in a slump, then the relationship is probably weak.
Figure 1.2 provides a hypothetical example of what weak and strong relationships might look like, using generic independent and dependent variables. The scatter plot (you’ll learn much more about these in Chapter 14) on the left side illustrates a weak relationship. The first thing to note is that the pattern is not very clear; there is a lot of randomness to it. The line of prediction, which summarizes the trend in the data, does tilt upward slightly, indicating there is a slight tendency for outcomes that are relatively high on the independent variable also tend to be relatively high on the dependent variable, but that trend is not apparent in the data points. The best way to appreciate how weak the pattern is on the left side is to compare it with the pattern on the right side, where you don’t have to look very hard to notice a stronger trend in the data. In this case, there is a clear tendency for high values on the independent variable to be associated with high values on the dependent variable, indicating a strong, positive relationship
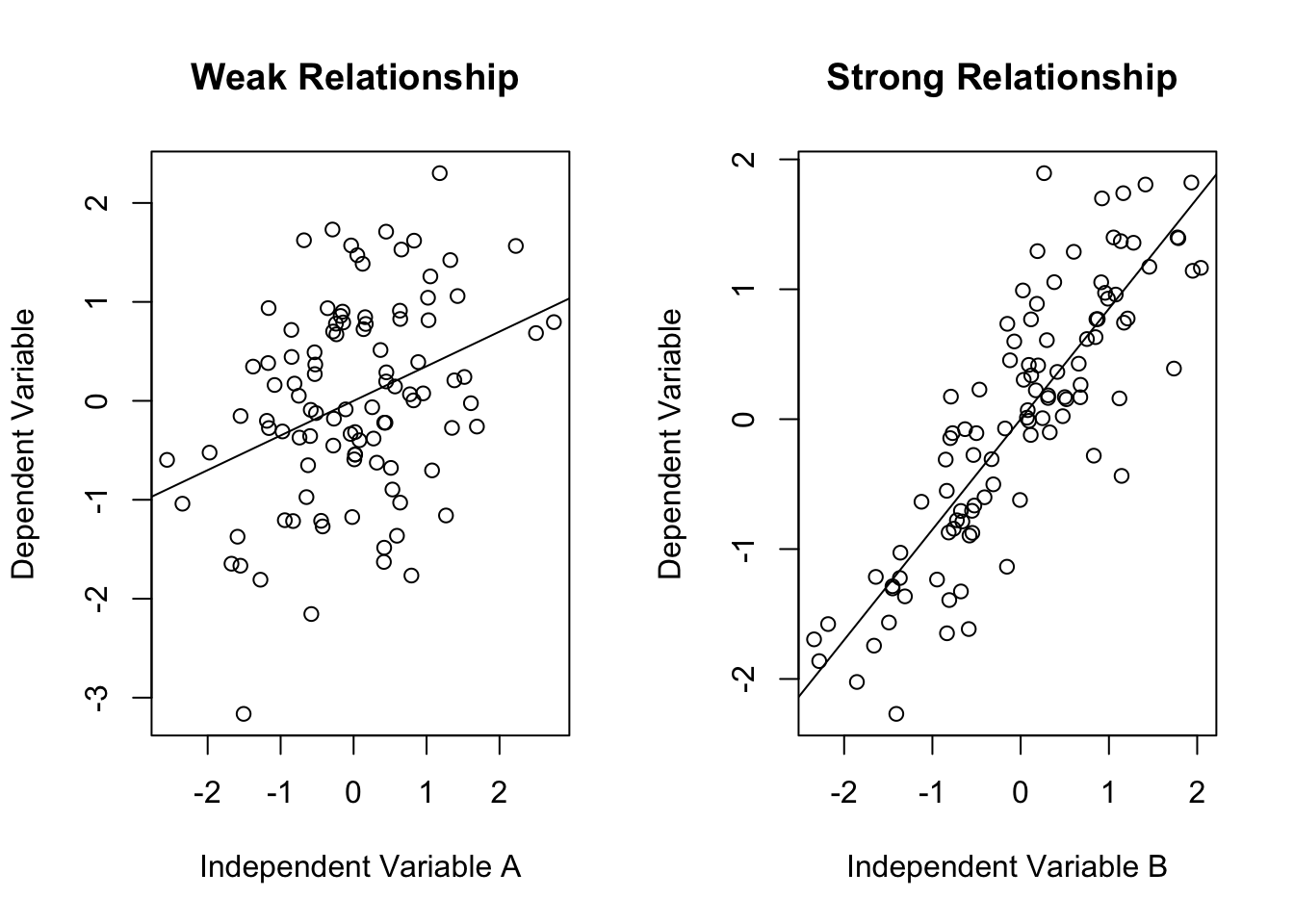
Figure 1.2: Simulated examples of Strong and Weak Relationships
Figure 1.2 provides a good example of data visualization, a form of presentation that can be a very important part of communicating research results. The idea behind data visualization is to display research findings graphically, primarily to help consumers of research contextualize and understand the findings.
To appreciate the importance of visualization, suppose you do not have the scatterplots shown above but are instead presented with the correlations reported in Table 1.3. These correlations are statistics that summarize how strong the relationships are, with values close to 0 meaning there is not much of a relationship, and values closer to 1 indicating strong relationships (more on this in Chapter 14). If you had these statistics but no scatter plots, you would understand that Independent Variable B is more strongly related to the dependent variable than Independent Variable A is, but you might not fully appreciate what this means in terms of the predictive capacity of the two independent variables. The scatter plots help with this a lot.
| Independent Variable A | Independent Variable B | |
|---|---|---|
| Correlation | .35 | .85 |
At the same time, while the information in Figure 1.2 gives you a clear intuitive impression of the differences in the two relationships, you can’t be very specific about how much stronger the relationship is for independent variable B without more precise information such as the correlation coefficients in Table 1.3. Most often, the winning combination for communicating research results is some mix of statistical findings and data visualization.
In addition to measuring the strength of relationships, researchers also focus on their level of confidence in the findings. This is a key part of hypothesis testing and will be covered in much greater detail later in the book. The basic idea is that we want to know if the evidence of a relationship is strong enough that we can rule out the possibility that it occurred due to chance, or perhaps to measurement issues. Consider the relationship between Independent Variable A and the dependent variable in Figure 1.2. On its face, this looks like a weak relationship. In fact, without the line of prediction or the correlation coefficient, it is possible to look at this scatterplot and come away with the impression the pattern is random and there is no relationship between the two variables. The correlation (.35) and line of prediction tell us there is a positive relationship, but it doesn’t look very different that a completely random pattern. From this perspective, the question becomes, “How confident can we be that this pattern is really different from what you would expect if there was no relationship between the two variables?” Usually, especially with large samples, researchers can have a high level of confidence in strong relationships. However, weak relationships, especially those based on a small number of cases, do not inspire confidence. This might be a bit confusing at this point, but good research will distinguish between confidence and strength when communicating results. This point is emphasized later, beginning in Chapter 10.
One of the most important parts of this stage of the research process is the interpretation of the results. The key point to get here is that the statistics and visualizations do not speak for themselves. It is important to understand that knowing how to type in computer commands and get statistical results is not very helpful if you can’t also provide a coherent, substantive explanation of the results. Bottom line: Use words!
Typically, interpretations of statistical results focus on how well the findings comport with the expectations laid out in the hypotheses, paying special attention to both the strength of the relationships and the level of confidence in the findings. A good discussion of research findings will also acknowledge potential limitations to the research, whatever those may be.
By way of example, let’s look at a quick analysis of the relationship between economic growth (measured as the percentage change in real GDP per capita during the first three quarters of the election year) and votes for the incumbent party presidential candidate (measured as the incumbent party candidate’s percent of the two-party national popular vote), presented in Figure 1.3. Note that in the scatter plot, the circles represent each outcome and the year labels have been added to make it easier for the reader to relate to and understand the pattern in the data (you will learn how to create graphs like this later in the book).
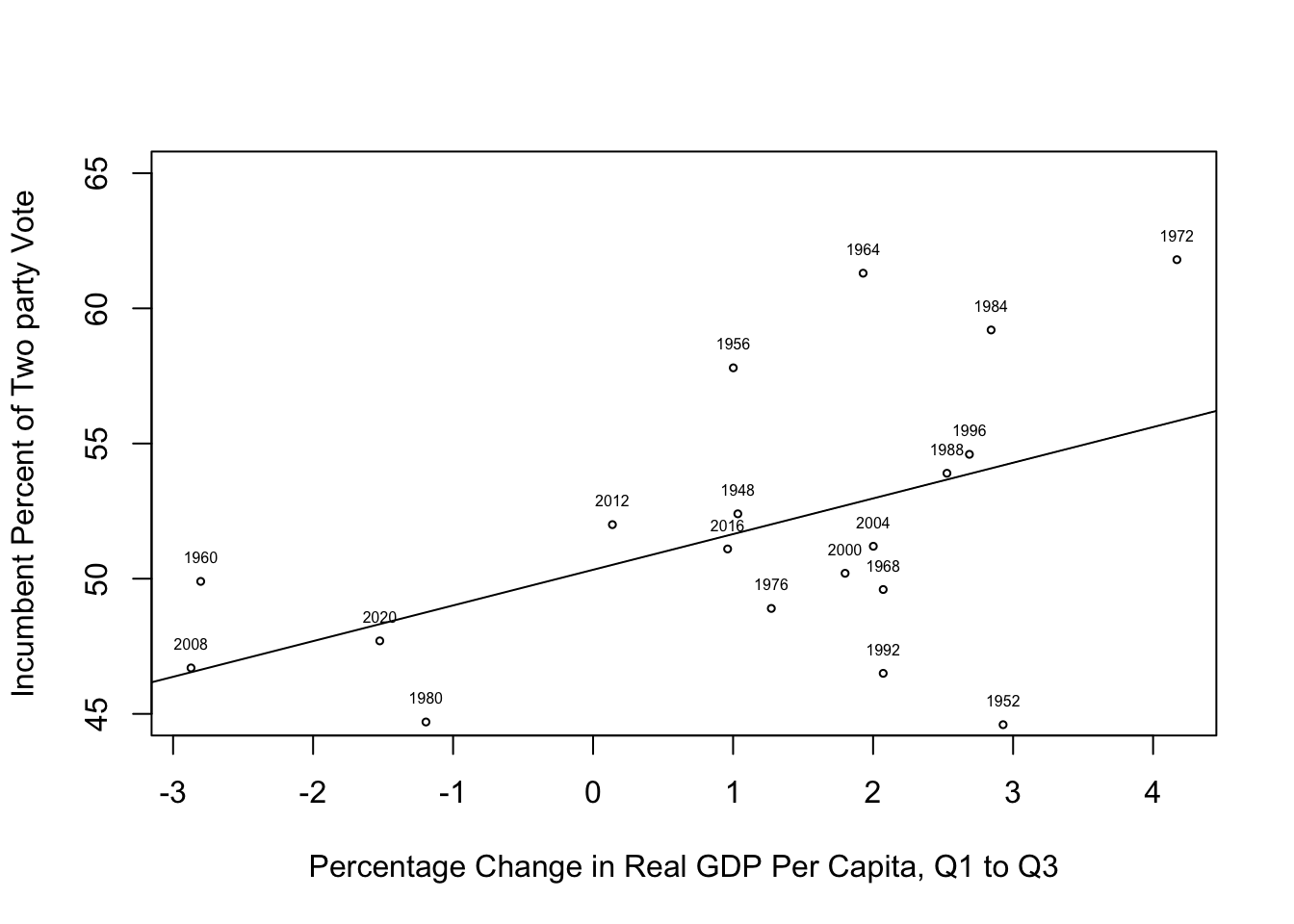
Figure 1.3: A Simple Test of the Retrospective Voting Hypothesis
Here is an example of the type of interpretation, based on these results, that makes it easier for the research consumer to understand the results of the analysis:
The results of the analysis provide some support for the retrospective voting hypothesis. The scatter plot shows that there is a general tendency for the incumbent party to struggle at the polls when the economy is relatively weak and to have success at the polls when the economy is strong. However, while there is a positive relationship between GDP growth and incumbent vote share, it is not a strong relationship. This can be seen in the variation in outcomes around the line of prediction, where we see a number of outcomes (1952, 1956, 1972, 1984, and 1992) that deviate quite a bit from the anticipated pattern. The correlation between these two variables (.49), confirms that there is a moderate, positive relationship between GDP growth and vote share for the incumbent presidential party. Clearly, there are other factors that help explain incumbent party electoral success, but this evidence shows that the state of the economy does play a role.
1.3.4 Feedback
Although it is generally accepted that theories should not be driven by what the data say (after all, the data are supposed to test the theory!), it would be foolish to ignore the results of the analysis and not allow for some feedback into the research process and reformulation of expectations. In other words, it is possible that you will discover something in the analysis that leads you to modify your theory, or at least change the way you think about things. In the real world of social science data analysis, there is a lot of back-and-forth between theory, hypothesis formation, and research findings. Typically, researchers have an idea of what they want to test, perhaps grounded in some form of theory, or maybe something closer to a solid rationale; they then gather data and conduct some analyses, sometimes finding interesting patterns that influence how they think about their research topic, even if they had not considered those things at the outset.
Let’s consider the somewhat modest relationship between change in GDP and votes for the incumbent party, as reported in Figure 1.3. Based on these findings, you could conclude that there is a tendency for the electorate to punish the incumbent party for economic downturns and reward it for economic upturns, but the trend is not strong. Alternatively, you could think about these results and ask ourselves if you are missing something. For instance, you might consider the sort of conditions in which you should expect retrospective voting to be easier for voters. In particular, if the point of retrospective voting is to reward or punish the incumbent president for outcomes that occur during their presidency, then it should be easier to assign responsibility in years in which the president is running for another term. Several elections in the post-WWII era were open-seat contests, meaning that the incumbent president was not running, mostly due to term limits (1952, 1960, 1968, 1988, 2000, 2008, and 2016). It makes sense that the relationship between economic conditions and election outcomes should be weaker during these years, since the incumbent president can only be held responsible indirectly. So, maybe you need to examine the two sets of elections (incumbent running vs. open seat) separately before you conclude that the retrospective model is only somewhat supported by the data.
Figure 1.4 illustrates how important it can be to allow the results of the initial data analysis to provide feedback into the research process. On the left side, there is a fairly strong, positive relationship between changes in GDP in the first three quarters of the year and the incumbent party’s share of the two-party vote when the incumbent is running. There are a couple of years that deviate from the trend, but the overall pattern is much stronger here than it was in Figure 1.3, which included data from all elections. In addition, the scatterplot for open-seat contests (right side) shows that when the incumbent president is not running, there is virtually no relationship between the state of the economy and the incumbent party share of the two-party vote. These interpretations of the scatter plot patterns are further supported by the correlation coefficients, .68 for incumbent races and a meager .16 for open-seat contests.
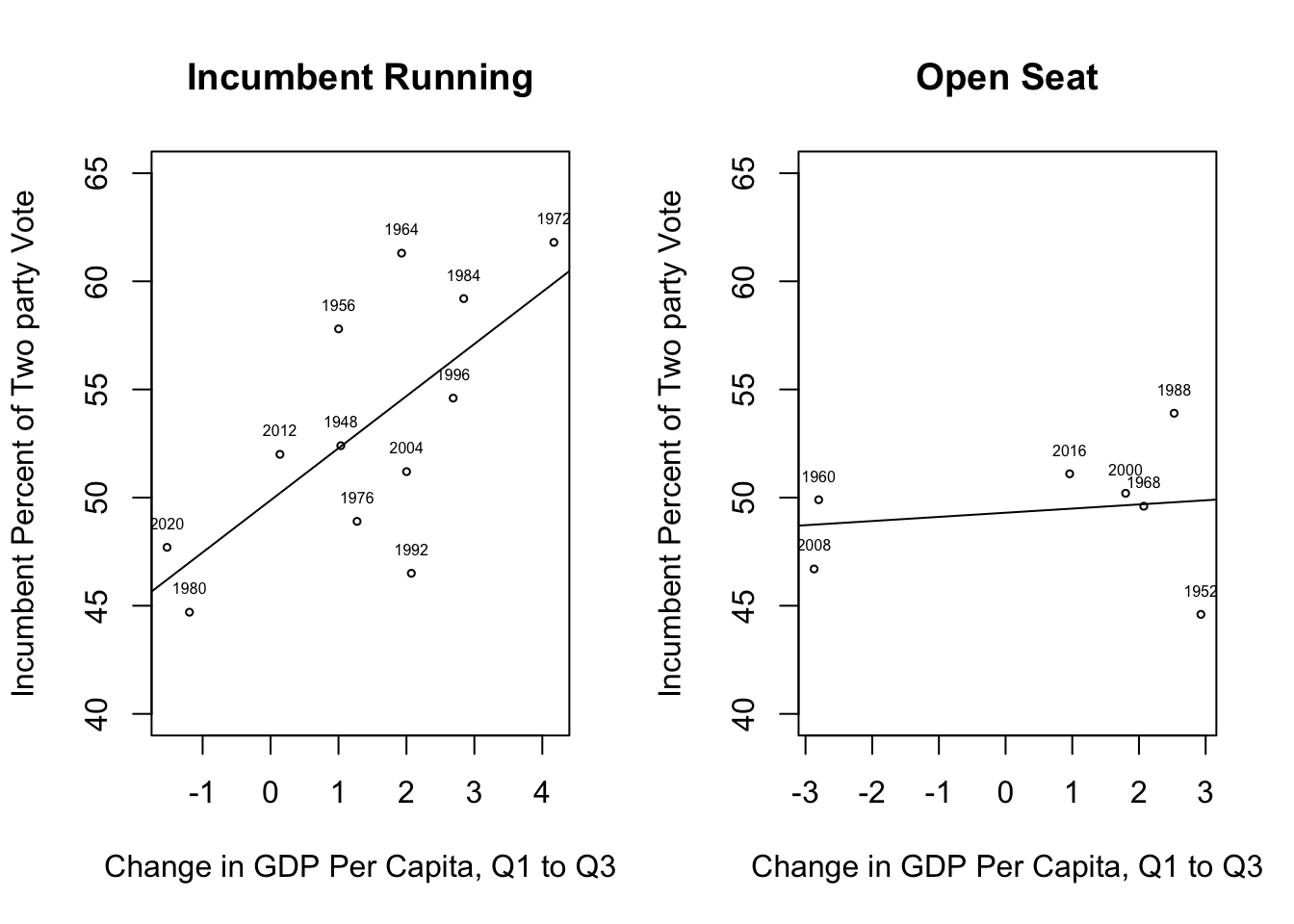
Figure 1.4: Testing the Reptrospective Voting Hypothesis in Two Different Contexts
The lesson here is that it can be very useful to allow for some fluidity between the different components of the research process. When theoretically interesting possibilities present themselves during the data analysis stage, they should be given due consideration. Still, with this new found insight, it is necessary to exercise caution and not be over-confident in the results, in large part because they are based on only 19 elections. With such a small number of cases, the next two or three elections could alter the relationship in important ways if they do not fit the pattern of outcomes in Figure 1.4. This would not be as concerning if the findings were based on a larger sample of elections.
1.4 Observational vs. Experimental Data
Ultimately, when testing hypotheses about how two variables are related to each other, we are saying that we think outcomes on the independent variable help shape outcomes on the dependent variable. In other words, we are interested in making causal statements. Causation, however, is very difficult to establish, especially when working with observational data, which is the type of data used in this book. You can think of observational data as measures of outcomes that have already occurred. As the researcher, you are interested in how X influences Y, so you gather data on already existing values of X and Y to see if there is a relationship between the two variables. A major problem is that there are multiple other factors that might produce outcomes on X and Y and, try as we might, it is very difficult to take all of those things into account when assessing how X might influence Y.
Experimental data, on the other hand, are data produced by the researcher, and the researcher is able to manipulate the values of the independent variable completely independent of other potential influences. Suppose, for instance, that we wanted to do an experimental study of retrospective voting in mayoral elections. We could structure the experiment in such a way that all participants are given the same information (background characteristics, policy positions, etc.) about both candidates (the incumbent seeking reelection and their challenger), but one-third of the participants (Group A) would be randomly assigned to receive information about positive outcomes during the mayor’s term (reduced crime rate, increased property values, etc.), while another third (Group B) would receive information about negative outcomes (increased crime rate, decreased property values, etc.) during the mayor’s term, and the remaining third of the respondents (Group C) would not receive any information about local conditions during the mayor’s term. If, after receiving all of the information treatments, participants in Group A (positive information) give the mayor higher marks and are generally more supportive than participants in Groups B (negative information) & C (no information), and members of Group C are more supportive of the mayor than members of Group B, we could conclude that information about city conditions during the mayor’s term caused these differences because the only difference between the three groups is whether they got the positive, negative, or no information on local conditions. In this example, the researcher is able to manipulate the information about conditions in the city independent of all other possible influences on the dependent variable.
This is not to say that experimental data do not have serious drawbacks, especially when it comes to connecting the experimental evidence to real-world politics. Consider, for instance, that the experimental scenario described above bears very little resemblance to the way voters encounter candidates and campaigns in real world election. However, within the confines of the experiment itself, any differences in outcomes between Group A and Group B can be attributed to the difference in how city-level conditions were presented to the two groups.
The most important thing to remember when discussing linkages between variables is to be careful about the language you use to describe those relationships. What this means is to understand the limits of what you can say regarding the causal mechanisms, while at the same time speaking confidently about what you think is going on in the data.
1.4.1 Necessary Conditions for Causality
One way you can gain confidence in the causal nexus between variables is by thinking about the necessary conditions for causality. By “necessary” conditions I mean those conditions that must be met if there is a causal relationship. These should not be taken as sufficient conditions, however. The best way to think of these conditions is that if one of them is not met, then there is no causal relationship. If they are all met, then you are on surer footing but still don’t know that one variable “causes” the other. Meeting these conditions means that a causal relationship is possible.
Let’s look at these conditions using an example related to the retrospective voting hypothesis. Suppose we have a public opinion survey in which respondents were asked for their evaluation of the state of the national economy (Better, Worse, or the Same as a year ago) in the first wave of the survey, before the 2020 election, and were then asked how they voted (Trump, Biden, Other) in the second wave of the survey, immediately following the election. Presumably, Trump did better among those who had positive views of the economy, and Biden did better among those with negative views. Pretty basic, I know. By the way, is this an example of using observational data or experimental data?5
Time order. Given our current understanding of how the universe operates, if X causes Y, then X must occur in time before Y. This seems pretty straightforward in the example used here. In the case of economic perceptions and vote choice in 2020, the independent variable (economic attitudes) is measured in the pre-election wave of the survey and presumable developed before votes were cast.
Covariation. There must be an empirically discernible relationship between X and Y. If evaluations of the state of the economy influence vote choice, then candidate support should vary across categories of economic evaluations, as spelled out in the hypothesis. In fact, using responses from the 2020 ANES survey, there is covariation between these two variables: only 26% of respondents who thought the economy was doing worse reported voting for President Trump, compared to 60% among those who thought the economy was the same and 84% among those who thought the economy was doing better.
Non-spurious. A spurious relationship between two variables is one that is produced by a third variable that is related to both the independent and dependent variables. In other words, while there may be a statistical relationship between perceptions of the economy and vote choice, the relationship could reflect a third (confounding) variable that “causes” both accessing material and course grade. Remember, this is a problem with observational data but not experimental data.
Based on the discussion above, the primary interest is in the direct relationship between X (economic evaluations) and Y (vote choice). This is illustrated with the arrow from economic evaluations and vote choice in Figure 1.5. There is, in fact, a strong relationship between these two variables, and this finding has held for most elections in the past fifty years. What we have to consider, however, is whether this relationship might be the spurious product of a confounding variable (Z) that is related to both X and Y. In this case, the most obvious candidate for a confounding variable is party identification. It stands to reason that most Democrats in 2020 reported negative evaluations of the economy (as is usually the case for challenging party partisans) and most Republicans reported positive evaluations of the economy (as is usually the case for in-party partisans), and at the same time, Democrats voted overwhelmingly for Biden, as Republicans did for Trump, on the basis of their partisan ties.
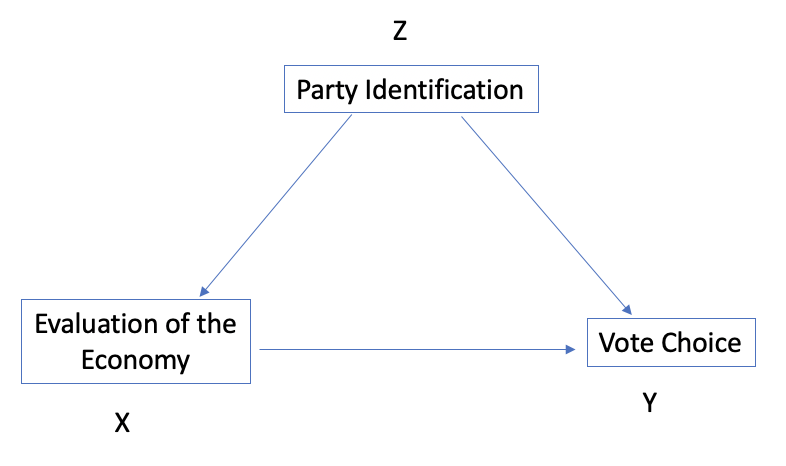
Figure 1.5: Controlling for a Third Variable
So, the issue is that the observed relationship between economic evaluations and vote choice might be reflecting the influence of party identification on both variables rather than the direct effect of the economic evaluations. This problem is endemic to much of social science research and needs to be addressed head-on, usually by incorporating potentially confounding variables into the analysis. Methods for addressing this issue are addressed at greater length in later chapters.
Theoretical grounding. Are there strong theoretical reasons for believing that X causes Y? This takes us back to the earlier discussion of the importance of having clear expectations and a sound rationale for pursuing your line of research. This is important because variables are sometimes related to each other coincidentally and may satisfy the time-order criterion and the relationship may persist when controlling for other variables. But if the relationship is nonsensical, or at least seems like a real theoretical stretch, then it should not be assigned any causal significance. In the case of economic evaluations influencing vote choice, the hypothesis is on a strong theoretical footing.
Even if all of these conditions are met, it is important to remember that these are only necessary conditions. Satisfying these conditions is not a sufficient basis for making causal claims. Causal inferences must be made very cautiously, especially in a non-experimental setting. It is best to demonstrate an awareness of this by being cautious in the language you use.
1.5 Levels of Measurement
A lot of what researchers are able to do at the data analysis stage of the research process is constrained by the type of data they use. One way in which the data may differ from variable to variable is in terms of level of measurement. Essentially, the level of measurement of a variable describes how quantitative the variable is. This is a very important concept because making appropriate choices of statistics to use for a particular problem depends upon the level of measurement for the variables under examination. Generally, variables are classified along three different categories of level of measurement:
1. Nominal level variables have categories or characteristics that differ in kind or quality only. There are qualitative differences between categories but not quantitative differences. Let’s suppose we are interested in studying different aspects of religion. For instance, we might ask survey respondents for their religious affiliation and end up collapsing their responses into the following categories:
Protestant
Catholic
Other Christian
Jewish
Other Religion
No Religion
Of course, we are interested in more than these six categories, but we’ll leave it like this for now. The key thing is that as you move from one category to the next, you find different types of religion but not any sort of quantifiable difference in the labels used. For instance, “Protestant” is the first category and “Catholic” is the second, but we wouldn’t say “Catholic” is twice as much as “Protestant”, or one more unit of religion than “Protestant.” Nor would we say that “Other Religion” (the fifth category listed) is one unit more of religion than “Jewish”, or one unit less than “No Religion.” These sorts of statements just don’t make sense, given the nature of this variable. One way to appreciate the non-quantitative essence of these types of variables is to note that the information conveyed in this variable would not change, and would be just as easy to understand if listed the categories in a different order. Suppose “Catholic” switched places with “Protestant”, and “Jewish” with “Other Christian,” as shown below. Doing so does not really affect how we react to the information we get from this variable.
Catholic
Protestant
Jewish
Other Christian
Other Religion
No Religion
A few other politically relevant examples of nominal-level variables are: region, marital status, race and ethnicity, and place of residence (urban/suburban/rural). Can you think of other examples?
2. Ordinal-level variables have categories or values that can be arranged in a meaningful order (the categories can be ranked) and for which it is possible to make greater/less than or magnitude-type statements, but without a lot of specificity. For instance, sticking with the example of measuring different aspects of religion, you might be interested in ascertaining the level of religiosity (how religious someone is) of survey respondents. You could ask a question something along the lines of, “In your day-to-day life, how important is religion to you?”, offering the following response categories:
Not at all important
Only slightly important
Somewhat Important
Very important
A few things to note about this variable. First, the categories have some, though still limited, quantitative meaning. In terms of the thing being measured—the importance of religion—the level of importance increases as you move from the first to the last category. The categories are ordered from lowest to highest levels of importance. This is why variables like these are referred to as ordinal or ordered variables. You can appreciate the ordered nature of this variable by seeing what happens when the categories are mixed up:
Very important
Not at all important
Somewhat Important
Only slightly important
In this configuration, the response categories don’t seem to make as much sense as they did when they were ordered by magnitude. Moving from one category to the next, there is no consistently increasing or decreasing level of importance of religion.
But ordered variables such as these still have limited quantitative content, primarily because equal differences between ordinal categories do not have equal quantitative meaning. We still can’t really say the response in the second category or the original variable (“only slightly important”) is twice as important as the response in the first category (“not at all important”). We can’t even say that the substantive difference between the first and second categories is the same as the substantive difference between the second and third categories. This is because the categories only represent differences in ranking of a trait from lowest to highest, not numeric distances.
Sometimes, ordinal variables may be hard to identify because the categories do not appear to range from “low” to “high” values. Take party identification, for instance, or political ideology, as presented below. In the case of party identification, you can think of the categories as growing more Republican (and less Democratic) as you move from “Democrat” to “Independent” to “Republican.” Likewise, for ideology, categories grow more conservative (and less liberal) as you move from “Liberal” to “Moderate” to “Conservative”.
| Party ID | Ideology |
|---|---|
| Democrat | Liberal |
| Independent | Moderate |
| Republican | Conservative |
Both nominal and ordinal variables are also referred to as categorical variables, emphasizing the role of labeled categories rather than numeric outcomes.
3. Interval and ratio level variables are the most quantitative in nature and have numeric values rather than category labels. This means that the outcomes can be treated as representing objective quantitative values, and equal numeric differences between categories have equal quantitative meaning. A true interval scale has an arbitrary zero point; in other words, zero does not mean “none” of whatever is being measured. The Fahrenheit thermometer is an example of this (zero degrees does not mean there is no temperature).6 Due to the arbitrary zero point, interval variables cannot be used to make ratio statements. For instance, it doesn’t make sense to say that a temperature of 40 degrees is twice as warm as that of 20 degrees! But it is 20 degrees warmer, and that 20 degree difference has the same quantitative meaning as the difference between 40 and 60 degrees. Ratio level variables differ from interval-level in that they have a genuine zero point. Because zero means none, ratio statements can be made about ratio-level variables. for instance, 20% of the vote is half the size of 40% of the vote. For all practical purposes, other than making ratio statements we can lump ratio and interval data together. Interval and ratio variables are also referred to as numeric variables.
To continue with the example of measuring religiosity, you might opt to ask survey respondents how many days a week they usually say at least one prayer. In this case, the response would range from 0 to 7 days, giving us a ratio-level measure of religiosity. Notice the type of language you can use when talking about this variable that you couldn’t use when talking about nominal and ordinal variables. People who pray three days a week pray two more days a week than those who pray one day a week and half as many days a week as someone who prays six days a week.
Divisibility of Data. It is also possible to distinguish between variables based on their level of divisibility. A variable whose values are finite and cannot be subdivided is a discrete variable. Nominal and ordinal variables are always discrete, and some interval/ratio variables are discrete (number of siblings, number of political science courses, etc). A variable whose values can be infinitely subdivided is a continuous variable (time, weight, height, temperature, % voter turnout, % Republican vote, etc). Only interval/ratio variables can be continuous, though they are not always. The table below helps organize information on levels of measurement and divisibility.
| Divisibility | ||
|---|---|---|
| Level of Measurement | Discrete | Continuous |
| Nominal | Yes | No |
| Ordinal | Yes | No |
| Interval | Yes | Yes |
| Ratio | Yes | Yes |
1.6 Level of Analysis
One other important characteristic of data is the level of analysis. Researchers in the social sciences typically study outcomes at the individual or aggregate levels. Usually, we consider Individual-level data as those that represent characteristics of individual people (or some other basic level, such as firms or businesses). These type of data sometimes are also referred to as micro data. For instance, you might be interested in studying the political attitudes of individuals with different racial and ethnic backgrounds. For this, you could use a public opinion survey based on a random sample of individuals, and the survey would include questions about political attitudes and the racial and ethnic background characteristics of the respondents.
Aggregate data are usually based on aggregations of lower-level (individual/micro) data to some higher level. These types of data sometimes are also referred to as macro data. In political science, the aggregate levels are usually something like cities, counties, states, or countries. For instance, instead of focusing on individual differences in political attitudes on the basis of race and ethnicity, you might be interested in looking at the impact of the racial composition of states on state-level outcomes in presidential elections.
It is important to be aware of the level of analysis because this affects the types of valid inferences and conclusions you can make. If your analysis is based on individual-level data, then the inferences you make should be limited to individuals; and if your analysis is based on aggregate data, then the inferences you make should be limited to the level of aggregation you are studying. Inferring behavior at one level of analysis based on data from another level can be fraught with error. For instance, when using individual-level data, African-American voters stand are the strongest Biden supporters in the 2020 elections (national exit polls show that 87% of black voters supported Biden, compared to 65% of Latino voters, 61% of Asian-American voters, and 41% of white voters). Based on this strong pattern among individuals, one might expect to finding a similar pattern between the size of the black population and support for Biden among the states. However, this inference is completely at odds with the state-level evidence: there is no relationship between the percent African-American and the Biden percent of the two-party vote among the states (the correlation is .009), largely because the greatest concentration of black voters is in conservative southern states. It is also possible that you could start with the state-level finding and erroneously conclude that African-Americans were no more or less likely than others to have voted for Biden in 2020, even though the individual-level data show high levels of support for Biden among African-American voters.
This type of error is usually referred to as an error resulting from the ecological fallacy, which can occur when making inferences about behavior at one level of analysis based on findings from another level. Although the ecological fallacy is most often thought of in the context of making individual-level inferences from aggregate patterns, it is generally unwise to make cross-level inferences in either direction. The key point here is to be careful of the language you use when interpreting the findings of your research.
1.7 Next Steps
This chapter reviewed a few of the topics and ideas that are important for understanding the research process. Some of these things may still be hard for you to relate to, especially if you have not been involved in a quantitative research project. Much of what is covered in this chapter will come up again in subsequent parts of the book, hopefully solidifying your grasp of the material. The next couple of chapters also cover foundational material. Chapter 2 focuses on how to access R and use it for some simple tasks, such as examining imported data sets, and Chapter 3 introduces you to some basic statistical tables and graphs. As you read these chapters, it is very important that you follow the R demonstrations closely. In fact, I encourage you to make sure you can access R (download it or use RStudio Cloud) and follow along, running the same R code you see in the book, so you don’t have to wait for an assignment to get your first hands on experience. A quick word of warning, there will be errors. In fact, I made several errors trying to get things to run correctly so I could present the results you see the next couple of chapters. The great thing about this is that I learned a little bit from every error I made. Forge ahead, make mistakes, and learn!
1.8 Exercises
1.8.1 Concepts and Calculations
Identify the level of measurement (nominal, ordinal, interval/ratio) and divisibility (discrete or continuous) for each of the following variables.
- Course letter grade
- Voter turnout rate (%)
- Marital status (Married, divorced, single, etc)
- Occupation (Professor, cook, mechanic, etc.)
- Body weight
- Total number of votes cast
- #Years of education
- Subjective social class (Poor, working class, middle class, etc.)
- % below poverty level income
- Racial or ethnic group identification
For each of the pairs of variables listed below, designate which one you think should be the dependent variable and which is the independent variable. Give a brief explanation.
- Poverty rate/Voter turnout
- Annual Income/Years of education
- Racial group/Vote choice
- Study habits/Course grade
- Average Life expectancy/Gross Domestic Product
- Social class/happiness
Assume that the topics listed below represent different research topics and classify each of them each of them as either a “political” or “social” topic. Justify your classification. If you think a topic could be classified either way, explain why.
- Marital Satisfaction
- Racial inequality
- Campaign spending
- Welfare policy
- Democratization
- Attitudes toward abortion
- Teen pregnancy
For each of the pairs of terms listed below, identify which one represents a concept, and which one is an operational variable.
- Political partcipation/Voter turnout
- Annual income/Wealth
- Restrictive COVID-19 Rules/Mandatory masking policy
- Economic development/Per capita GDP
What is a broad social or political subject area that interests you? Within that area, what is a narrower topic of interest? Given that topic of interest, what is a research question you think would be interesting to pursuing? Finally, share a hypothesis related to the research question that you think would be interesting to test.
A researcher asked people taking a survey if they were generally happy or unhappy with the way life was going for them. They repeated this question in a followup survey two weeks later and found that 85% of respondents provided the same response. Is this a demonstration of validity or reliability? Why?
In an introductory political science class, there is a very strong relationship between accessing online course materials and course grade at the end of the semester: Generally, students who access course material frequently tend to do well, while those who don’t access course material regularly tend to do poorly. This leads to the conclusion that accessing course material has a causal impact on course performance. What do you think? Does this relationship satisfy the necessary conditions for establishing causality? Address this question using all four conditions.
A scholar is interested in examining the impact of electoral systems on levels of voter turnout using data from a sample of 75 countries. The primary hypothesis is that voter turnout (% of eligible voters who vote) is higher in electoral systems that use proportional representation than in majoritarian/plurality systems.
- Is this an experimental study or an an observational study?
- What is the dependent variable, and what is its level of measurement?
- What is the independent variable, and what is its level of measurement?
- What is the level of analysis for this study?
This might be the only bibliographic references in this book: Fiorina, Morris,Retrospective Voting in American National Elections. 1981. Yale University Press.↩︎
The way I’ve described it above, this is an example of observational data. The give away is that we are not manipulating the independent variable. Instead, we are measuring evaluations of the economy as they exist.↩︎
Other examples include SAT scores, credit scores, and IQ scores.↩︎