10.1 Visualización

El primer paso para estudiar posibles relaciones entre variables es visualizarlos. Si tenemos dos variables medidas por cada miembro de la población o muestra que estamos investigando podemos generar un diagrama de disperción también conocido como scatterplot. En este tipo de visualización cada miembro de la muestra/población está representado por un punto, y las coordinadas del punto corresponde a las dos variables que hemos medido, en el eje horizontal y vertical respectivamente.

El las figura 10.1, vemos que la concentración de puntos suben de la izquierda a la derecha. Es decir cuando avanzamos en el eje horizontal avanzamos en el eje vertical también. Es un ejemplo de una correlación positiva, como podría ser edad y estatura.

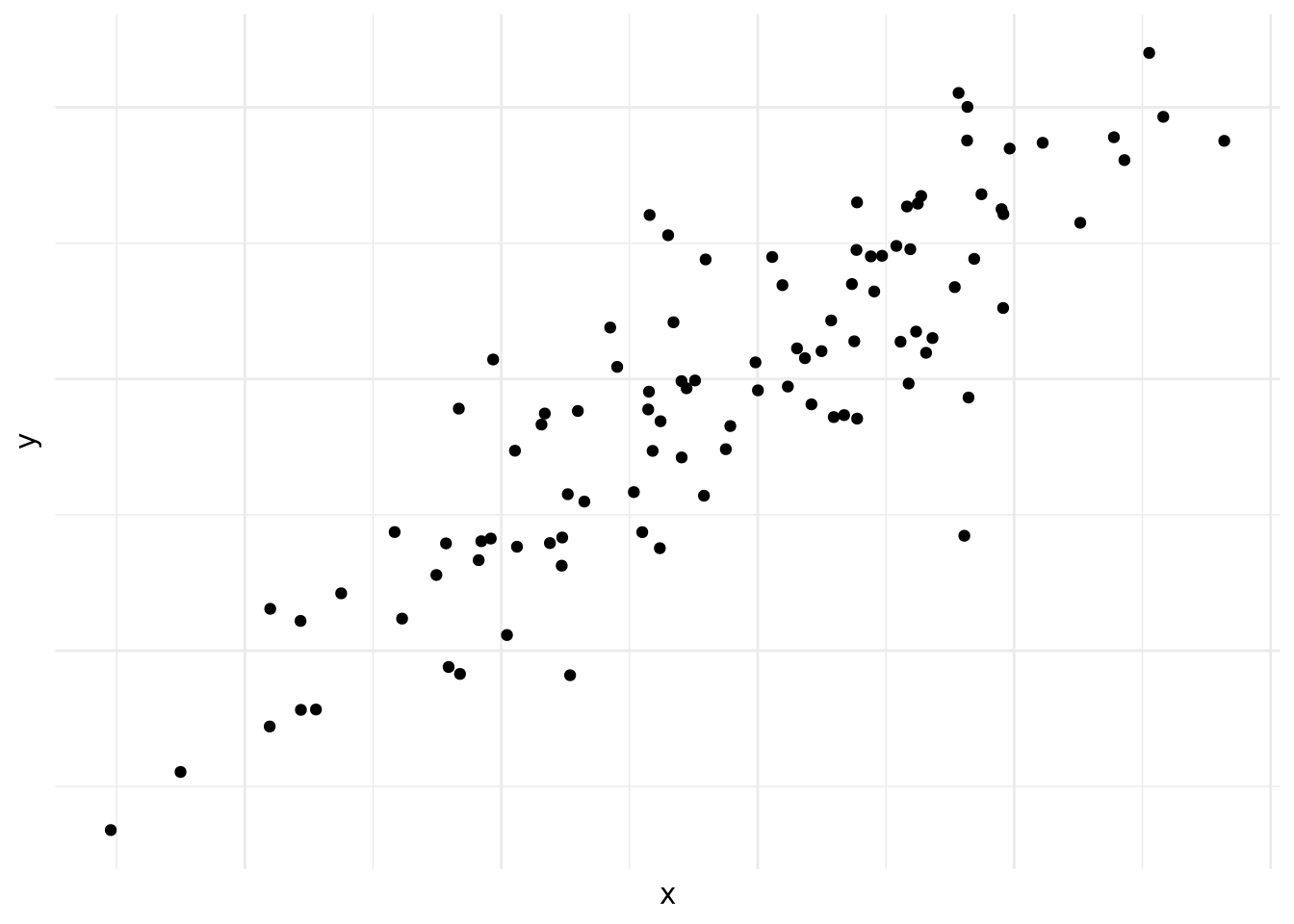
Figura 10.1: Correlación positiva

En la figura 10.2 vemos lo contrario, mientras avanzamos en el eje vertical retrocedemos (o bajamos) en el eje horizontal. Esto se conoce como correlacion negativa.

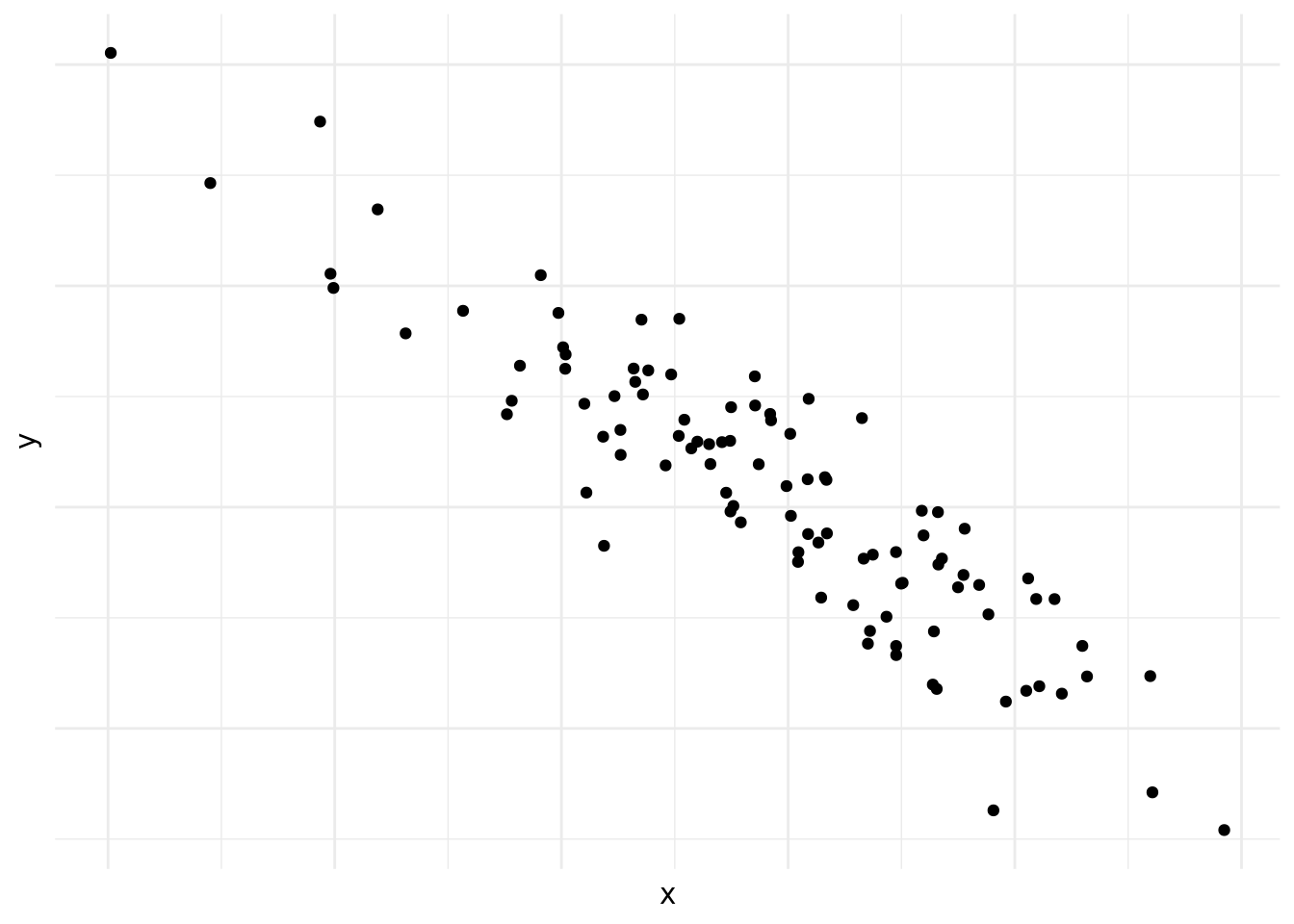
Figura 10.2: Correlación negativa

En la figura 10.3, también vemos correlación negativa, pero es menos fuerte que en la figura 10.2.

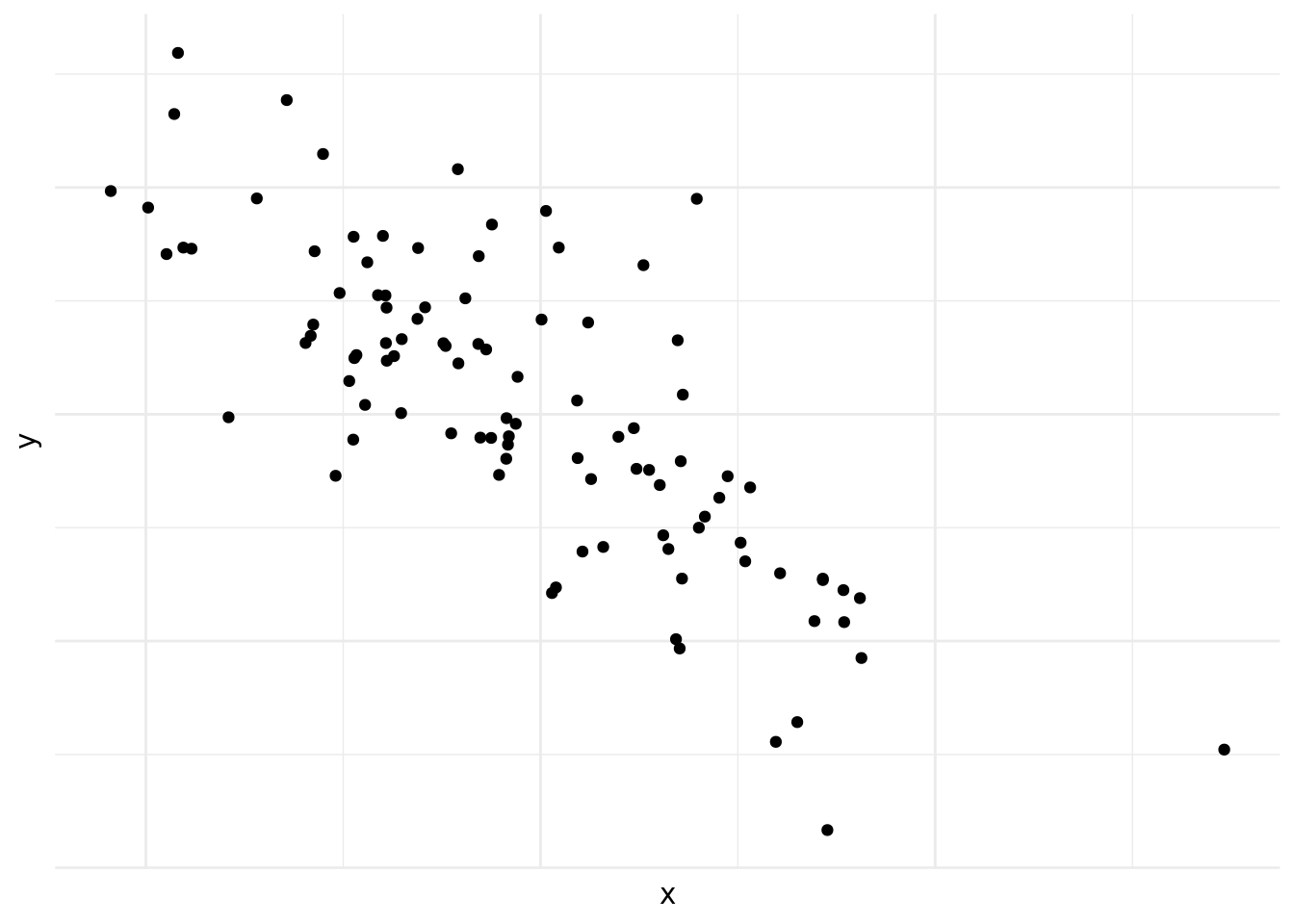
Figura 10.3: Correlación negative leve

En la figura 10.4 vemos una correlación negativa casi perfecta entre las dos variables.

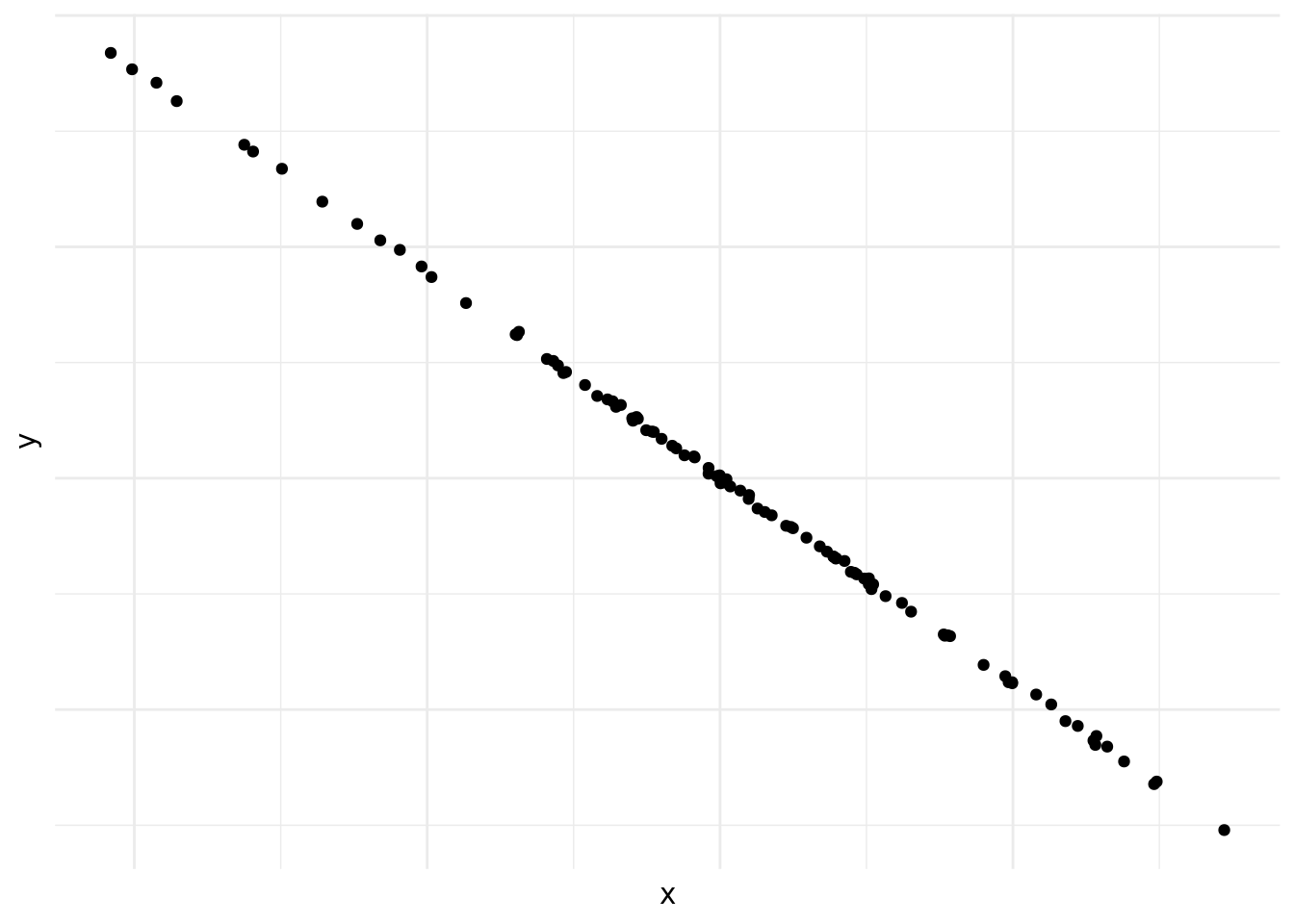
Figura 10.4: Correlación casi perfecta

En la figura 10.5 vemos un caso de correlación inexistente entre las variables en cuestión.

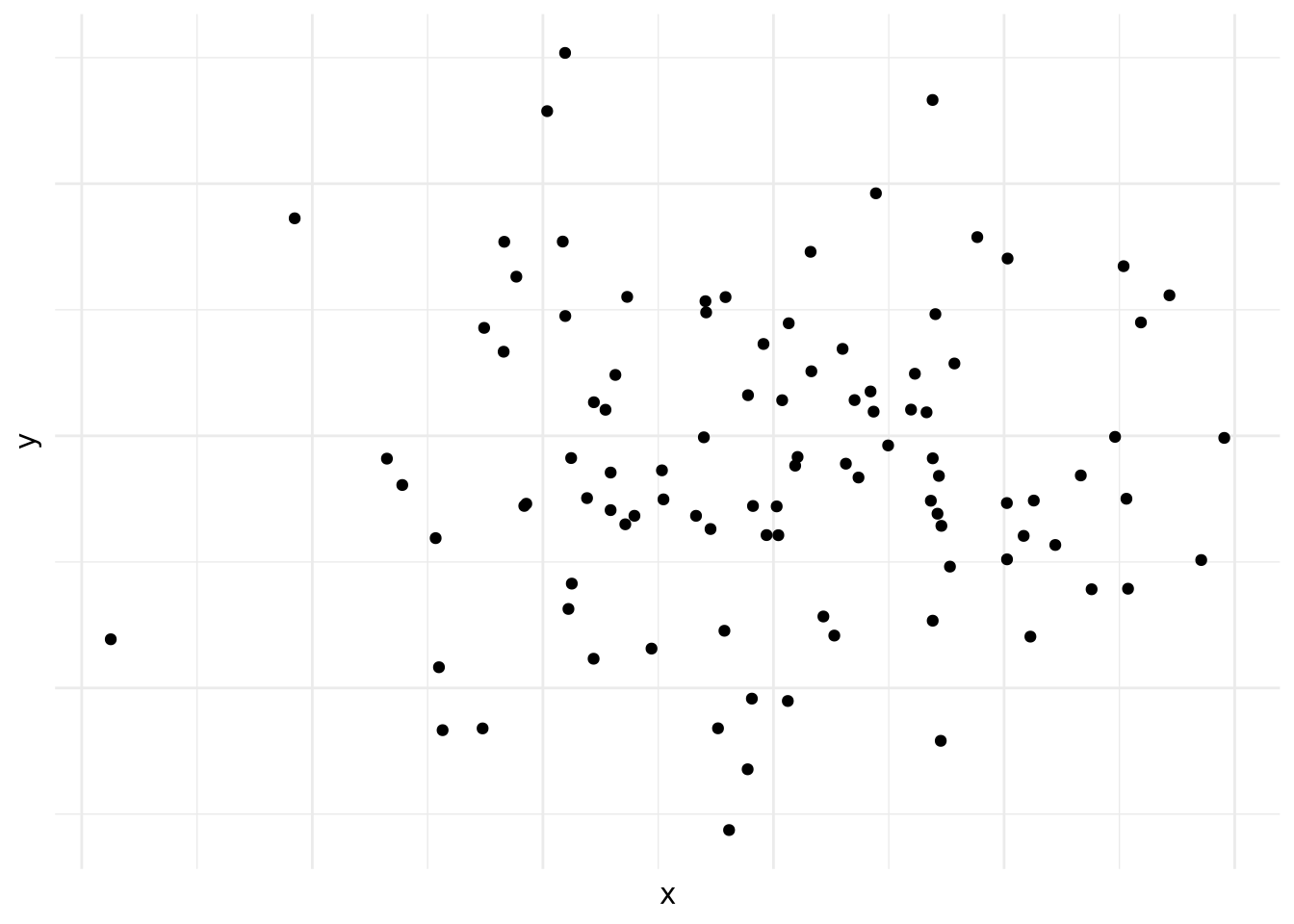
Figura 10.5: Correlación nula

En la figura 10.6 vemos que existe una relación entre las dos variables, pero que esta no es lineal.²¹

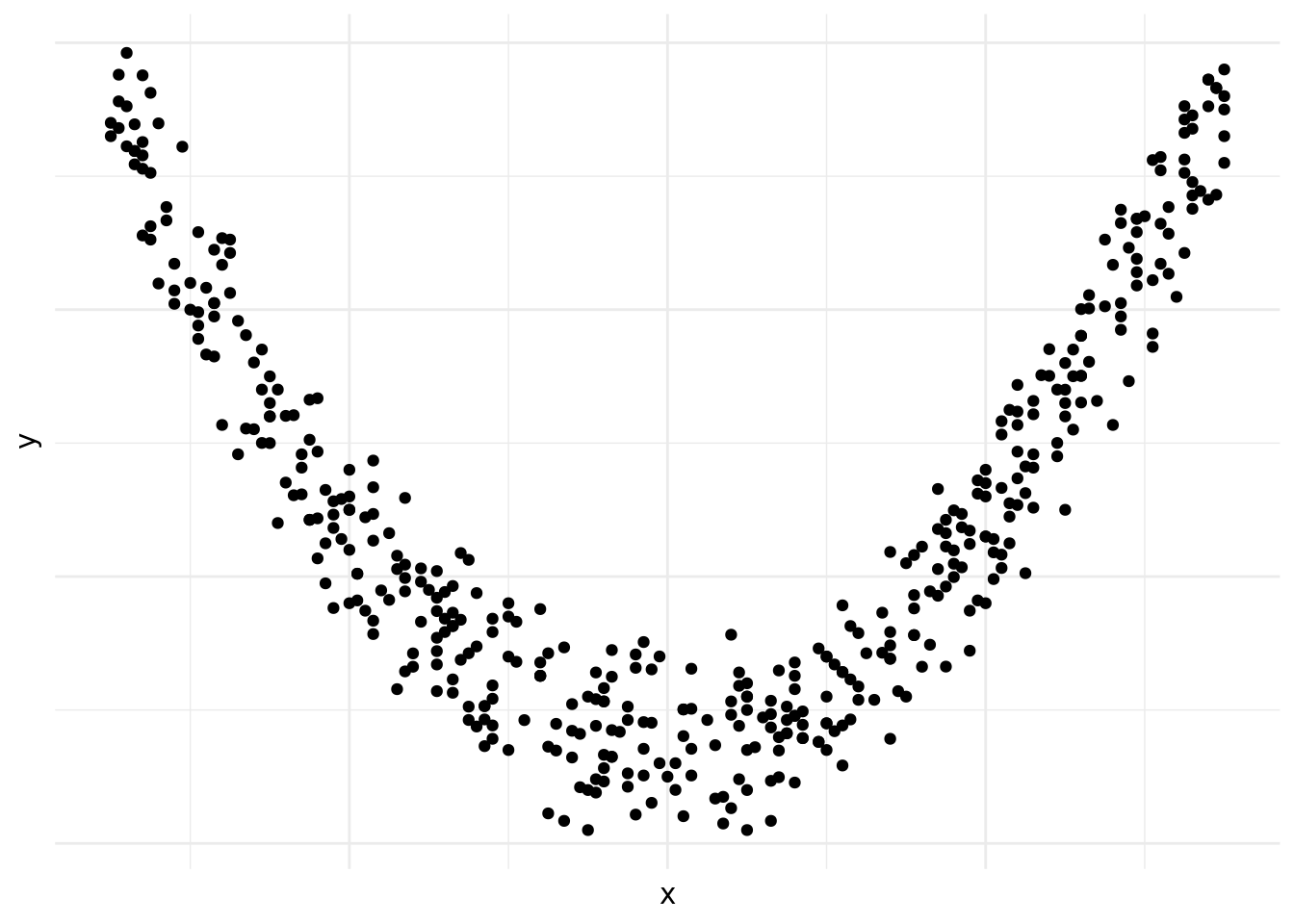
Figura 10.6: Relación no lineal

Las figuras 10.1, 10.2, 10.3, 10.4, 10.5 y 10.6 demuestran por qué es preciso graficar los datos al inicio del análisis. Nos da una indicación de si existe una correlación o no, si es positiva o negativa y que tan fuerte es. También nos podemos darnos cuenta de patrones en los datos que no son lineales, como es el caso de los datos en la figura 10.6. Asimismo, a veces nos encontramos con una correlación como la que vemos en la figura 10.4. Las correlaciones que son demasiado perfectas suelen ser un signo de advertencia y podemos preguntarnos si en realidad son dos variables distintas o si las dos están midiendo lo mismo.

Ejemplo 10.1 (Generar diagrama de dispersión en R)

# Generamos datos
datos = data.frame(
  x=rnorm(100),
  y=rnorm(100)
)

# Graficamos
plot(datos)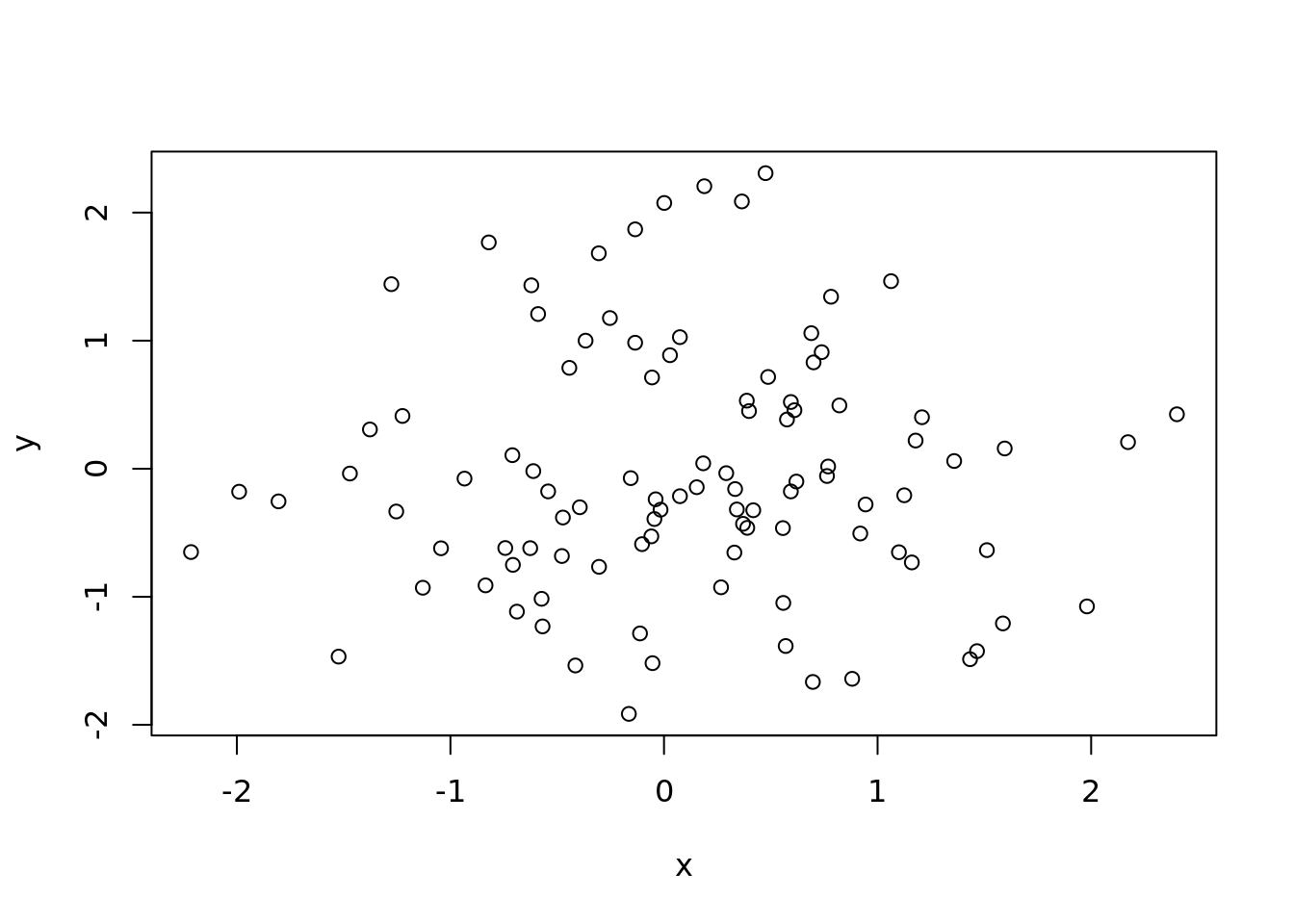

En el ejemplo 10.1 utilizamos la función rnorm para generar cien observaciones aleatorias con distribución normal y los ponemos dentro de un data.frame. Luego usamos la función plot para graficarlos. Como nuestro data.frame tiene solo dos columnas R entiende que estos son los datos que queremos graficar. Si el data.frame tiene más columnas, podemos especificar los que queremos graficar así:

plot(datos$x,datos$y)

Ejemplo 10.2 (Generar diagrama de dispersión en R)

Por defecto R viene con algunos data.frames ya cargados, uno de ellos es «trees», podemos usar la función head para ver las primeras seis filas.

head(trees)

##   Girth Height Volume
## 1   8.3     70   10.3
## 2   8.6     65   10.3
## 3   8.8     63   10.2
## 4  10.5     72   16.4
## 5  10.7     81   18.8
## 6  10.8     83   19.7

Vemos que tiene tres columnas «Girth», «Height» y «Volume» (circumferencia, alto y volumen), los que, por lógica, deben tener alta correlación. Graficamos dos de ellos.

plot(trees$Girth, trees$Volume)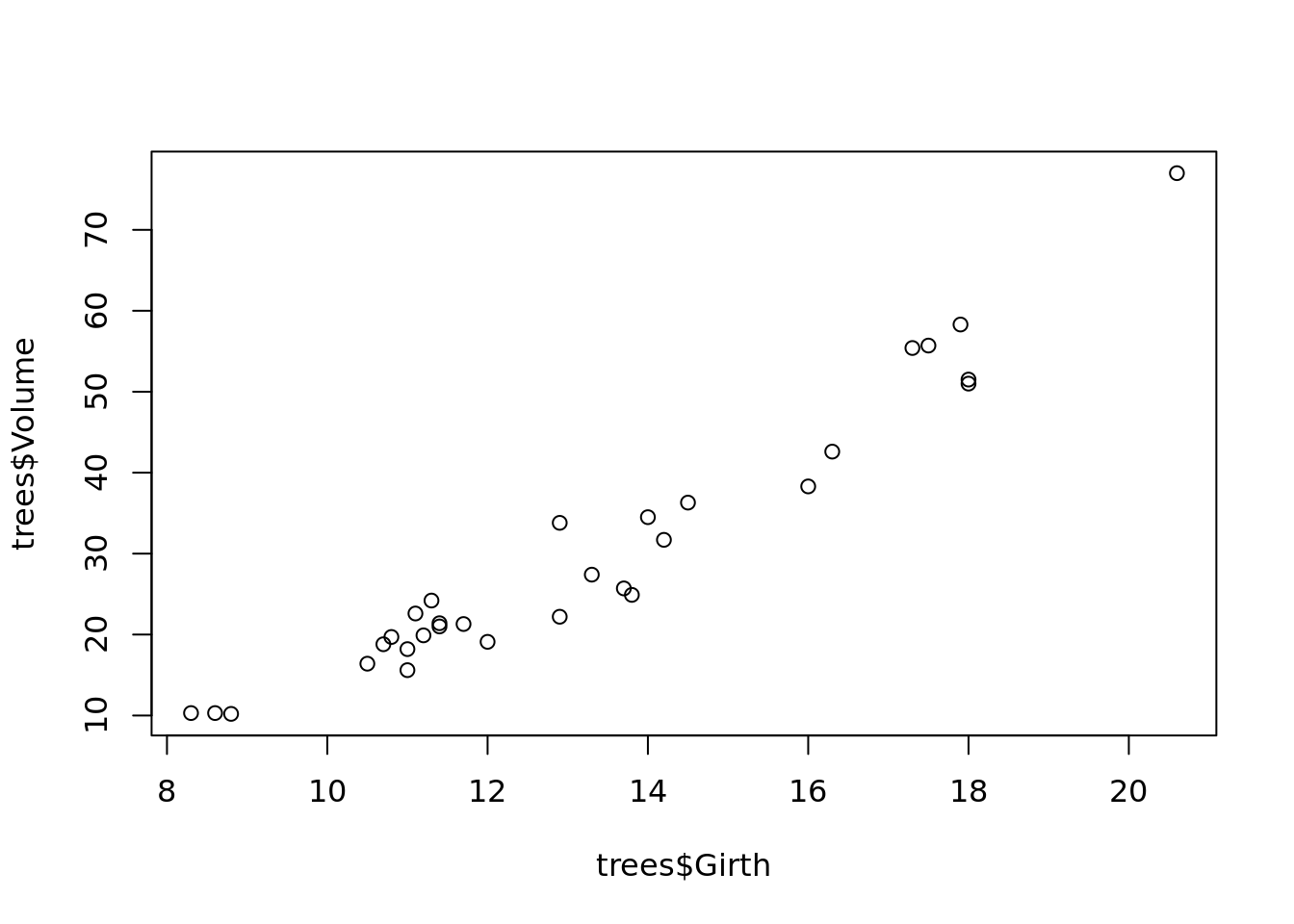

Si usamos la función plot sin especificar columnas R entiende que queremos ver todas las combinaciones.

plot(trees)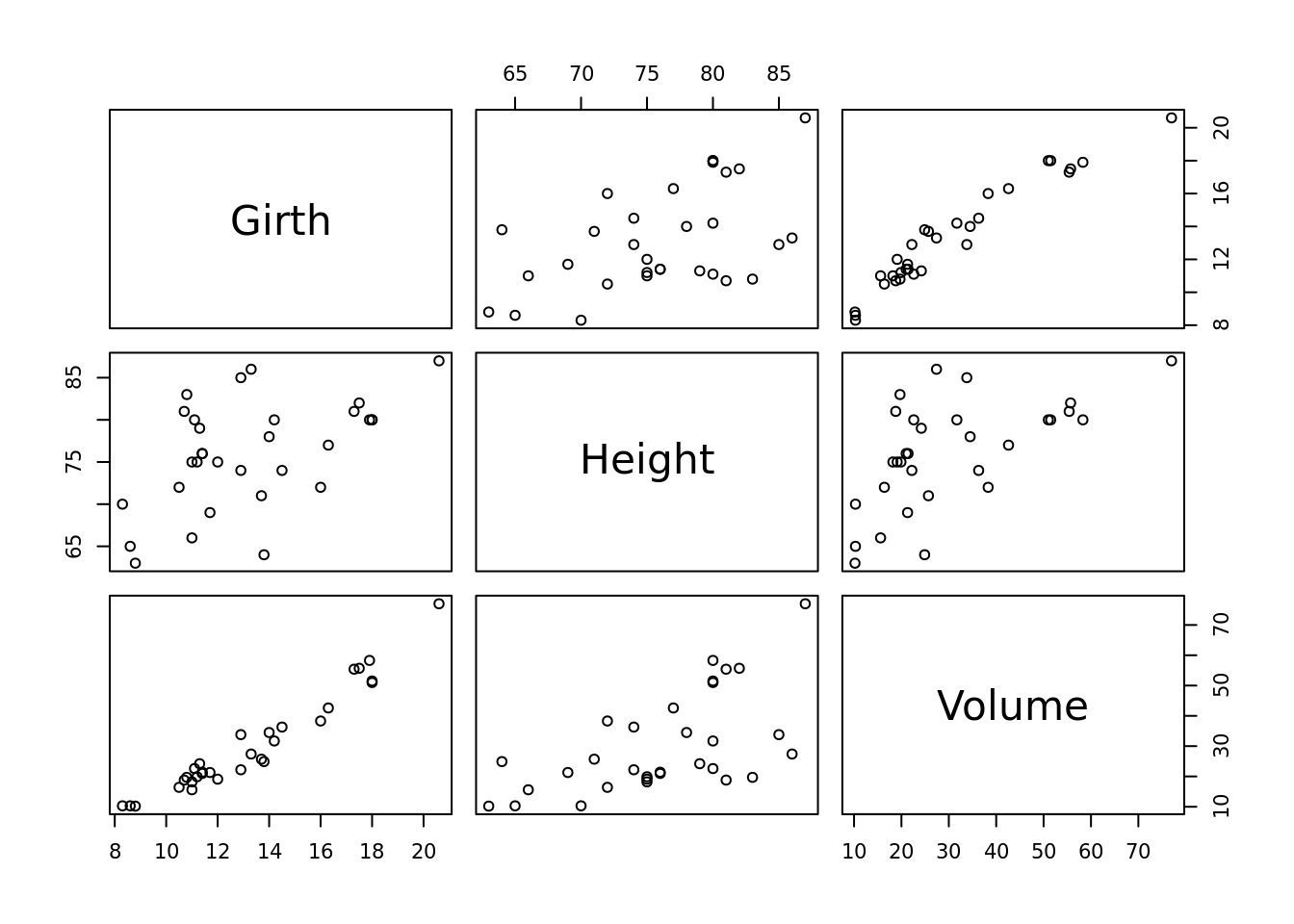

Este tipo de visualización puede ser útil cuando tenemos algunas variables y queremos darnos cuenta qué correlaciones hay. La visualización funciona bien hasta cierto número de columnas –ocho más o menos–, luego se vuelve difícil de leer y por ende de interpretar.

De hecho es cuadrática: \(y~\sim~x^2\).↩︎