5.1 Distribución muestral
Si suponemos que la estatura promedio de las argentinas entre 19 y 49 años es de 161 centímetros con una desviación estándar de 6,99, estos serían los parámetros de la población. Si sacamos cinco muestras aleatorias de veinte observaciones de esta población van a arrojar resultados distintos a estos valores. Algunas muestras van a tener una media por arriba de la media real y otras van a tener una media por debajo.
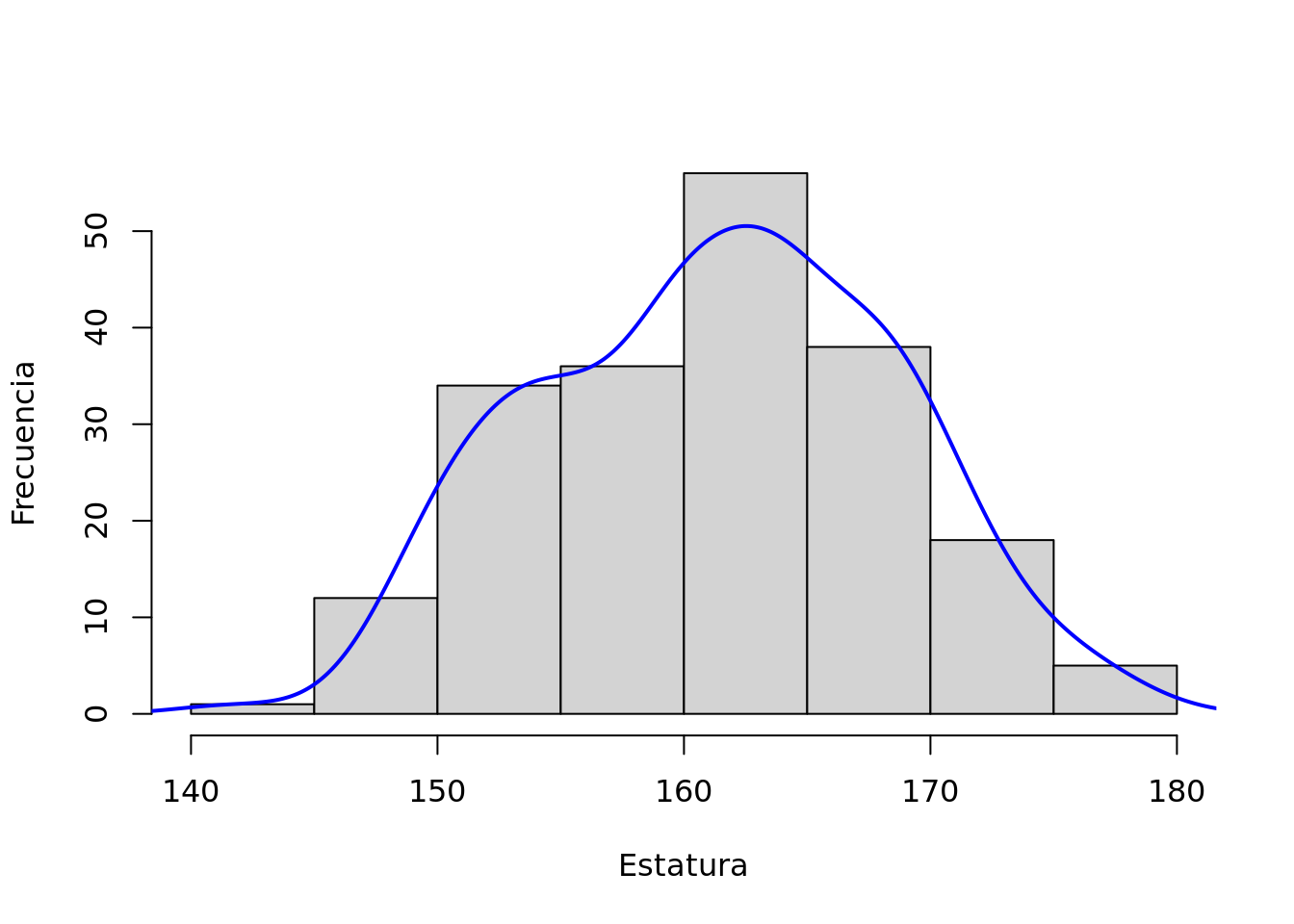
Figura 5.1: Cinco Muestras de 20 obseraciones
Como lo podemos observar en la figura 5.1 la distribución de las muestras es simétrica y normal. La media de nuestras muestras es 161,42; ligeramente por arriba de la media real, y la desviación estándar es de 6,17; más de medio centímetro por debajo de la desviación estándar de la población. La distribución muestral tiene algunas propiedades que son útiles para nuestro trabajo estadístico:
- Se aproxima a una distribución normal. Esto se conoce como el teorema del límite central.
- La media de la distribución es igual (o casi igual) a la media de la población.
- La dispersión es menor a la de la población general.
El número (3) de la lista tiene su lógica ya que en una muestra aleatoria un valor frecuente tiene más probabilidad de ser seleccionada que un valor extremo. La diferencia entre curva normal de la población y la curva de la distribución muestral está ilustrada en la figura 5.2.
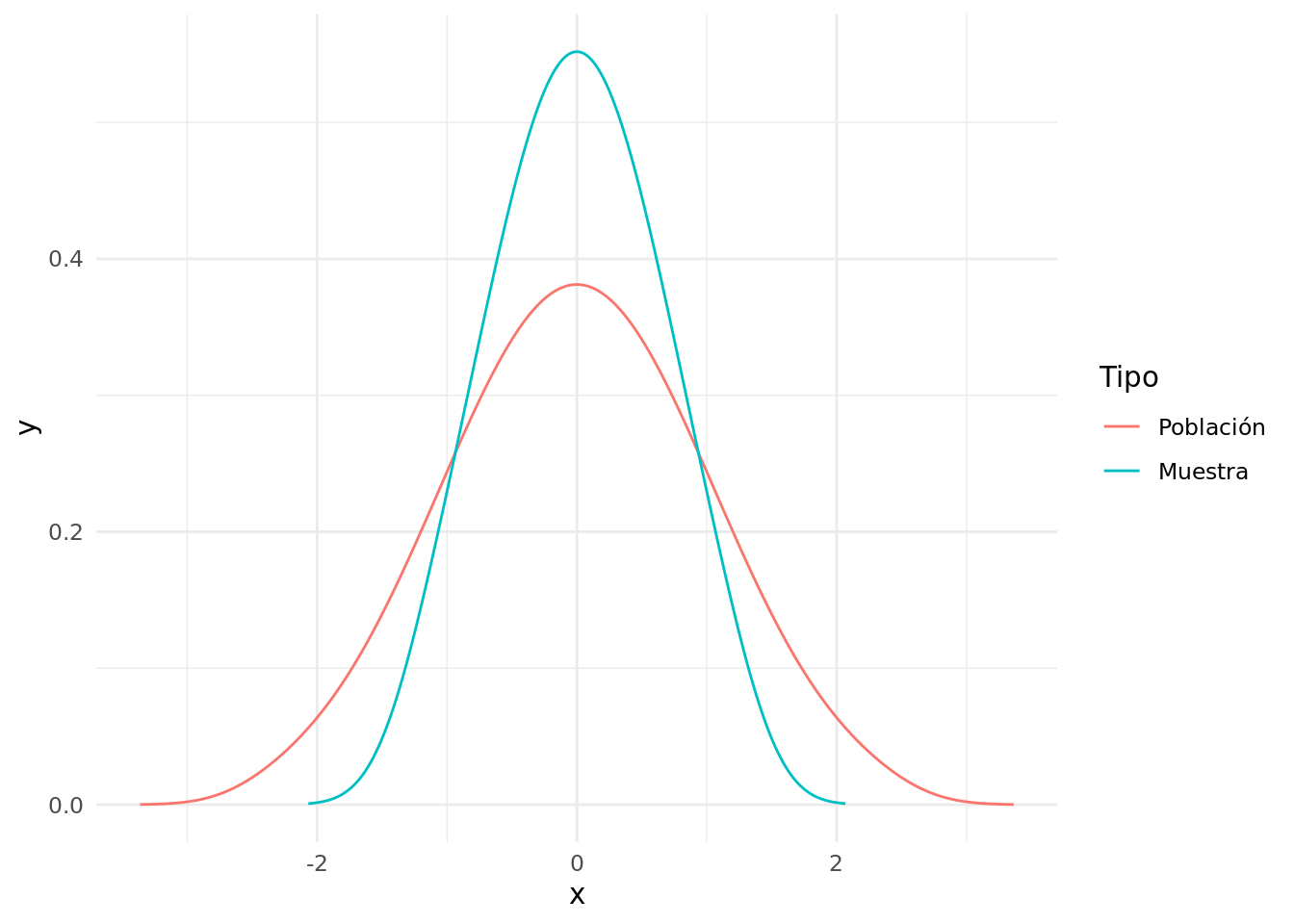
Figura 5.2: Distribución de la población y la muestra