Chapter 13 Triple Integrals
13.1 Definition of Triple Integral
Consider the function of three variables \(f(x,y,z)\), and a three-dimensional region \(V \subseteq \mathbb{R}^{3}\). The integral of \(f\) over \(V\), denoted \(\int \int \int_{V} f(x,y,z) \,dx \,dy \,dz\), is known as a triple integral. The definition of the triple integral is similar to that of a double integral.
Let \(\Delta x\), \(\Delta y\) and \(\Delta z\) be three sufficiently small real values. Consider a cuboid in the \((x,y,z)\)-space of length \(\Delta x\), width \(\Delta y\) and height \(\Delta z\). Fill \(V\) as efficiently as possible with these small cuboids. A typical cuboid has volume \(\Delta x \Delta y \Delta z\) and vertices:
\[\begin{align*}
(x_0,y_0,z_0), \qquad & \qquad (x_0+ \Delta x,y_0,z_0), \\
(x_0,y_0+ \Delta y,z_0), \qquad & \qquad (x_0,y_0,z_0+ \Delta z), \\
(x_0 + \Delta x,y_0 + \Delta y,z_0), \quad & \quad (x_0 + \Delta x,y_0,z_0 + \Delta z), \\
(x_0,y_0 + \Delta y,z_0 + \Delta z), \quad & \quad (x_0 + \Delta x,y_0 + \Delta y,z_0+ \Delta z).
\end{align*}\]
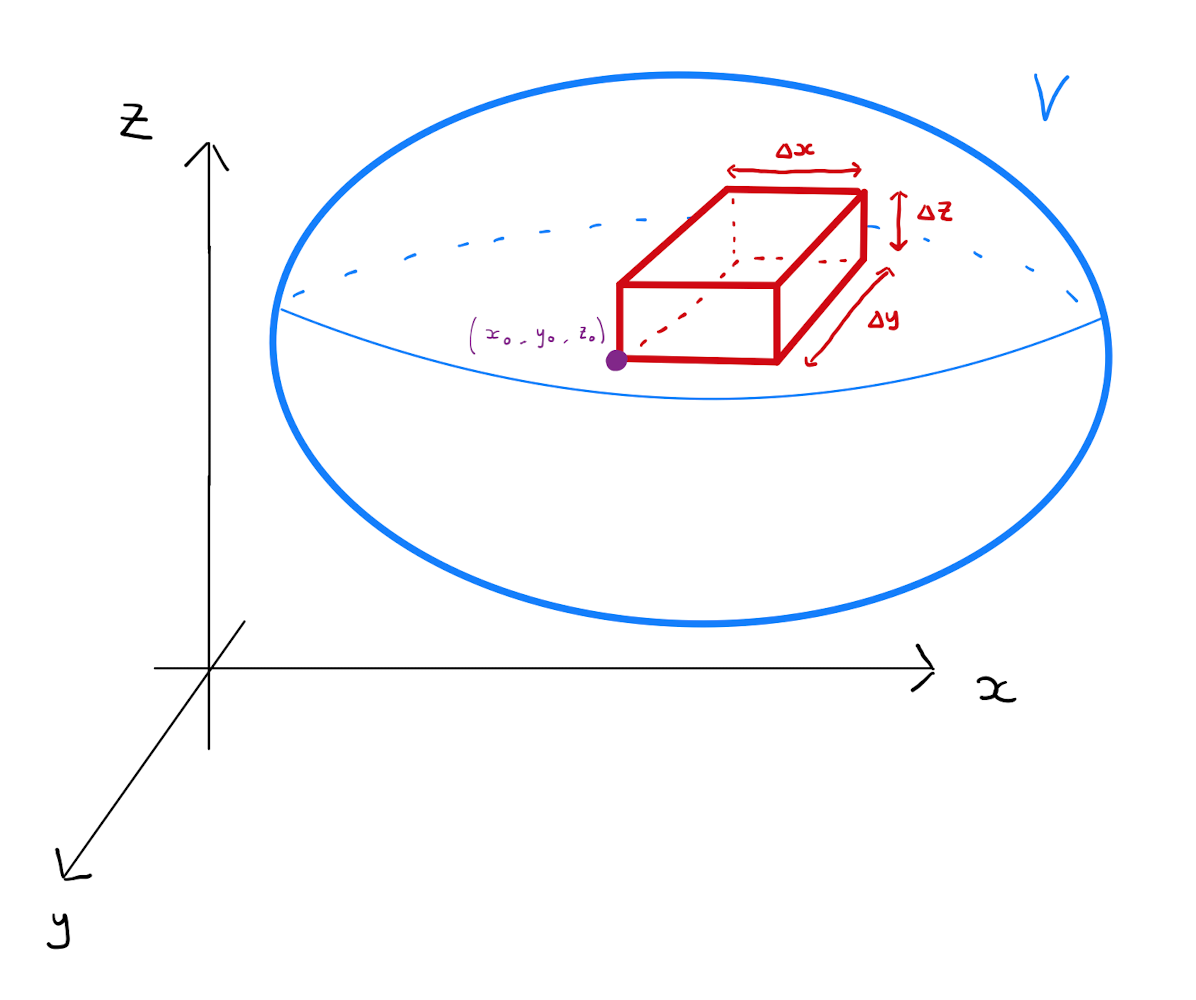
One can form the sum: \[\sum\limits_{\text{cuboids}} f(x_0,y_0,z_0) \Delta x \Delta y \Delta z.\] Consider the limiting process as \(\Delta x, \Delta y, \Delta z \rightarrow 0\). As this limits, the volume of each cuboid gets smaller, and \(V\) becomes more tightly packed with a greater number of cuboids. If the above summation tends to a limit, then this limit is defined as the tiple integral. Specifically
\[\sum\limits_{\text{cuboids}} f(x_0,y_0,z_0) \Delta x \Delta y \Delta z \quad \xrightarrow{\Delta x, \Delta y, \Delta z \rightarrow 0} \quad \int \int \int_V f(x,y,z) \,dx \,dy \,dz.\]
Computation of triple integrals can be difficult directly from the definition.
A triple integral can be evaluated as three nested single integrals. Specifically \[\int \int \int_V f(x,y,z) \,dx \,dy \,dz = \int_{z_1}^{z_2} \int_{y_1(z)}^{y_2(z)} \int_{x_1(y,z)}^{x_2(y,z)} f(x,y,z) \,dx \,dy \,dz,\] where
\(z_1\) is the smallest value that the \(z\)-coordinate takes over \(V\);
\(z_2\) is the largest value that the \(z\)-coordinate takes over \(V\);
\(y_1(\tilde{z})\) is the smallest value of the \(y\)-coordinate among points in \(V\) with \(z\)-coordinate equal to \(\tilde{z}\);
\(y_2(\tilde{z})\) is the largest value of the \(y\)-coordinate among points in \(V\) with \(z\)-coordinate equal to \(\tilde{z}\);
\(x_1(\tilde{y},\tilde{z})\) is the smallest value that the \(x\)-coordinate takes among all the points in \(V\) with \(y\)-coordinate equal to \(\tilde{y}\) and \(z\)-coordinate equal to \(\tilde{z}\);
\(x_2(\tilde{y},\tilde{z})\) is the largest value that the \(x\)-coordinate takes among all the points in \(V\) with \(y\)-coordinate equal to \(\tilde{y}\) and \(z\)-coordinate equal to \(\tilde{z}\).
Calculate the integral of \(f(x,y,z) = x+y z^2\) over the cube:
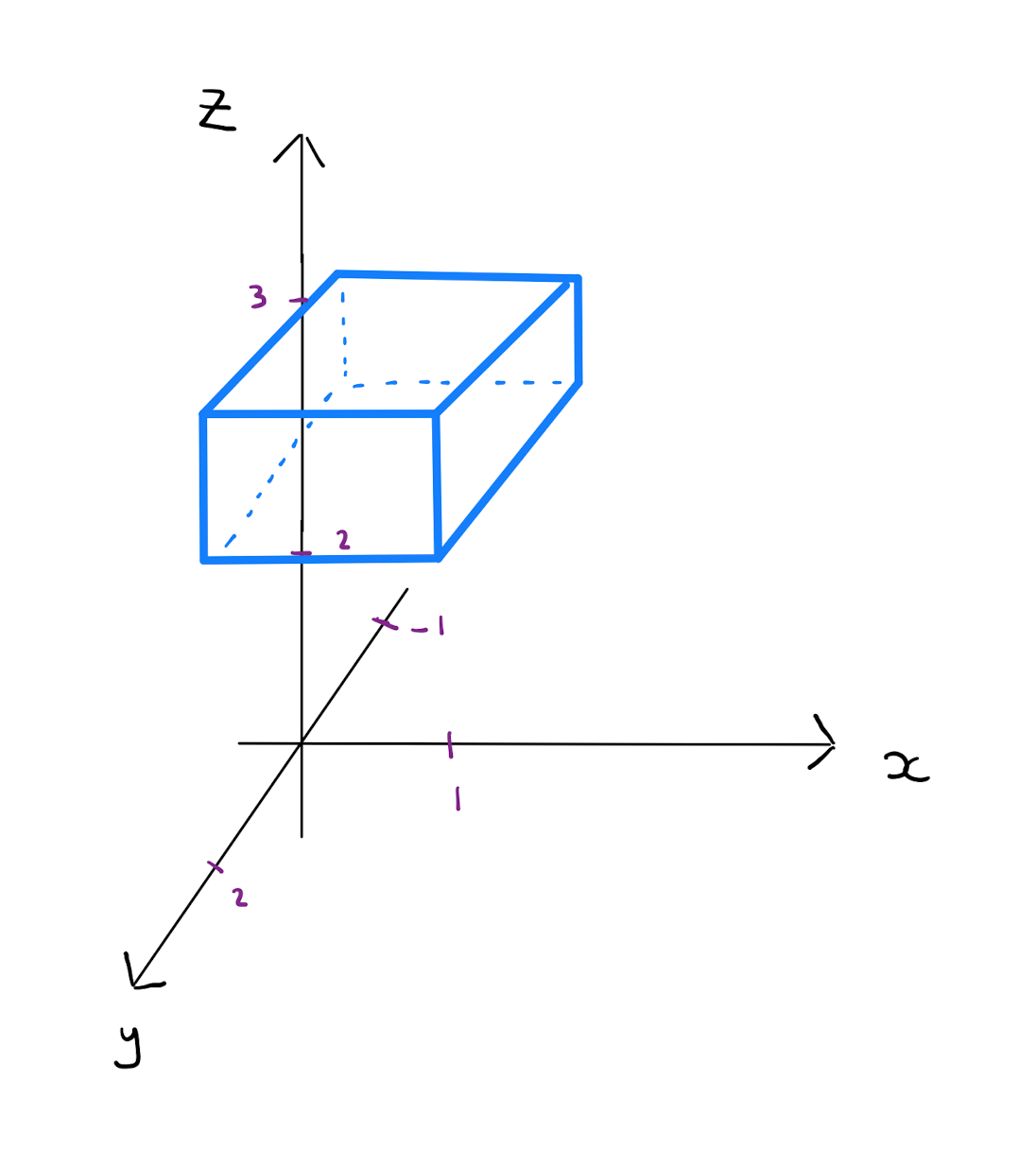
By applying Lemma 13.1.1, the integral can be evaluated as:
There are a number of applications of triple integrals such as center of masses, moments of inertia for 3d bodies and modelling fluid flows. The modules MATH2005: Vector Calculus and MATH2012: Modelling with Differential Equations are excellent opportunities to study more of these concepts.
Consider a three dimensional object \(V\) whose density is described by \(\rho(x,y,z)\). Then \[\text{Mass}(V) = \int \int \int_{V} \rho(x,y,z) \,dx \,dy \,dz.\]
Consider a three dimensional object \(V\). Define \[\bar{x} = \frac{\int \int \int_V x \,dx \,dy\,dz}{\int \int \int_V 1 \,dx \,dy\,dz}, \] and similarly define \(\bar{y}\) and \(\bar{z}\). Then the center of mass of \(V\) is given by \((\bar{x},\bar{y},\bar{z})\).
13.2 Change of Variables for Triple Integral
Consider a one-to-one transformation \(x=x(u,v,w)\), \(y=y(u,v,w)\) and \(z=z(u,v,w)\). Suppose one wanted to rewrite a triple integral \(\int \int \int_{V} f(x,y,z) \,dx \,dy \,dz\) in terms of the new variables \(u,v,w\). There is a result analogous to Theorem 12.2.3 that allows one to do this.
\[\int \int \int_V f(x,y,z) \,dx \,dy \,dz = \int \int \int_{V'} g(u,v,w) \lvert J \rvert \,du \,dv \,dw,\] where
\(g(u,v,w) = f \big( x(u,v,w), y(u,v,w), z(u,v,w) \big)\);
\(V' = \left\{ (u_0,v_0,w_0) : \big( x_0(u_0,v_0,w_0), y_0(u_0,v_0,w_0), z_0(u_0,v_0,w_0) \big) \in V \right\}\);
\(J\) is the Jacobian of the transformation \[J = \frac{\partial(x,y,z)}{\partial (u,v,w)} = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w} \end{vmatrix}. \]
The Jacobian \(J\) for a one-to-one transformation of three variables maintains many of the properties seen for the Jacobian of a two-variable transformation. In particular, \(J\) describes the volume in \((x,y,z)\)-space associated with small coordinate changes \(\Delta u,\Delta v, \Delta w\) in \((u,v,w)\)-space. Also provided a Jacobian is non-zero, then the Jacobian of the inverse is the reciprical: \(\frac{\partial (u,v,w)}{\partial (x,y,z)} = \frac{1}{\left( \frac{\partial (x,y,z)}{\partial (u,v,w)} \right)}\).
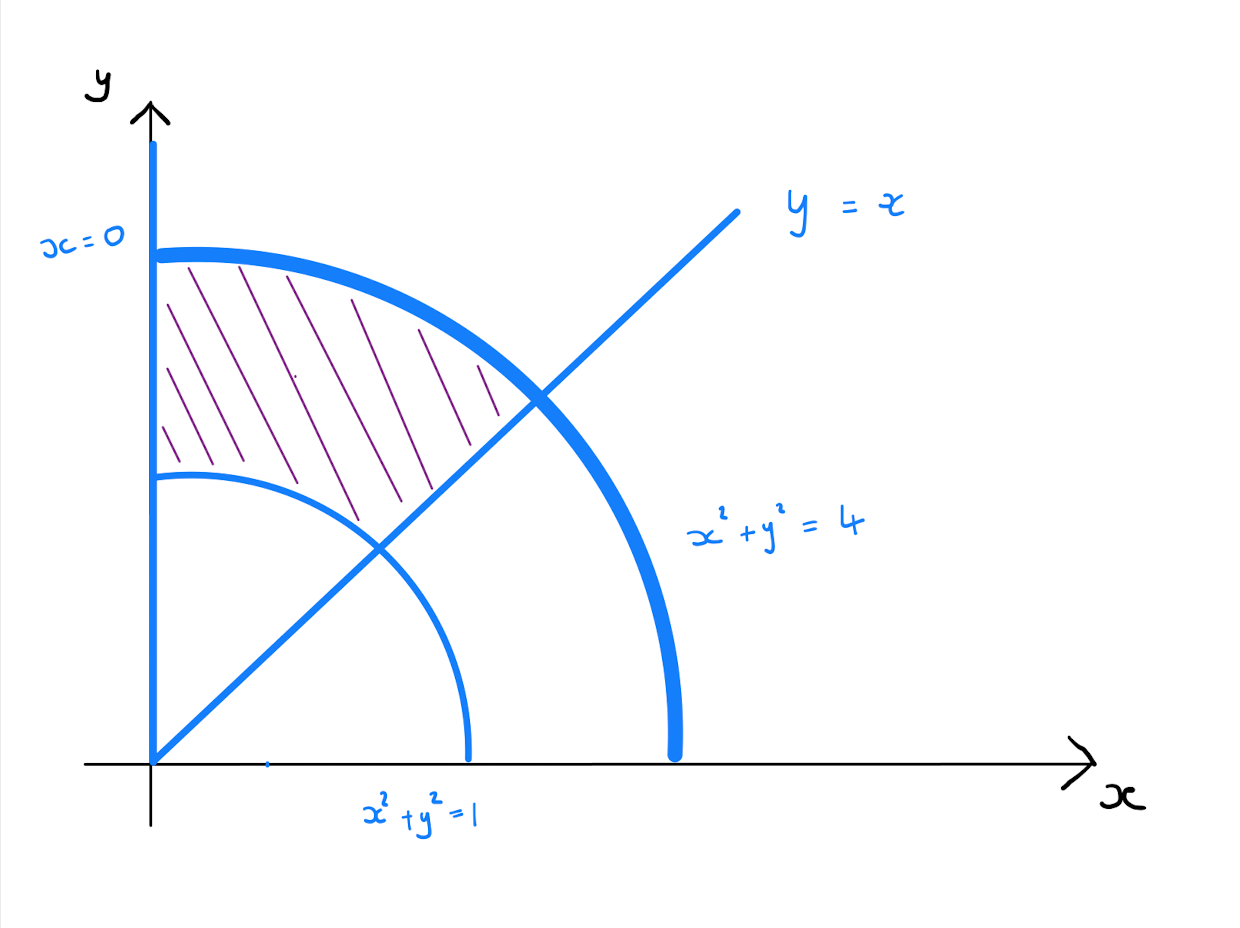
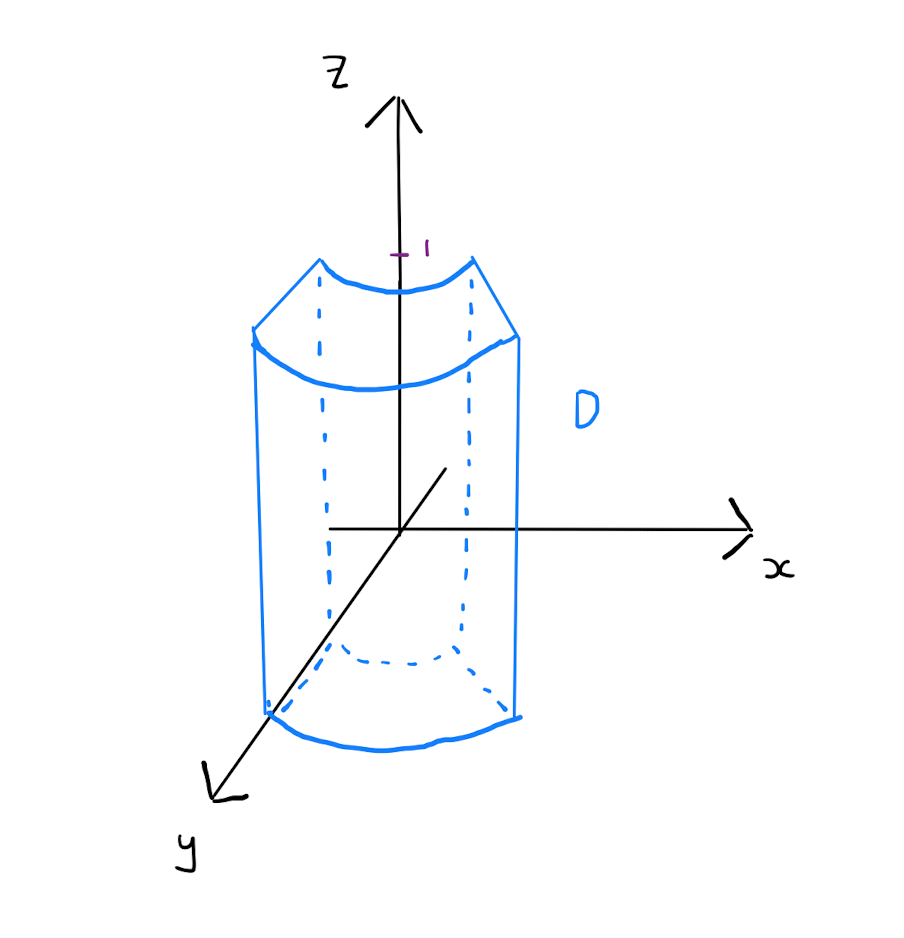
Evaluate \(I = \int \int \int_D x^2 + y^2 \,dx \,dy \,dz\) where \(D\) is the region in the first octant (\(x,y,z \geq 0\)) bounded by the cylinders \(x^2 + y^2 =1\) and \(x^2 + y^2 =4\), and the planes \(z=0\), \(z=1\), \(x=0\) and \(x=y\).
Due to the cylindrical nature of the problem, it may be beneficial to switch to cylindrical coordinates. In particular \[\begin{align*} x &= \rho \cos (\varphi), \\ y &= \rho \sin (\varphi), \\ z &= z. \end{align*}\]
Note \(f(x,y,z) = x^2 + y^2\), so
Now looking at the bounding lines of \(D\), and rewriting them in terms of \(\rho, \varphi\) and \(z\) by substitution, one obtains \[\begin{align*} x^2 + y^2 =1 \qquad &\text{becomes} \qquad \rho=1, \\[3pt] x^2 + y^2 =4 \qquad &\text{becomes} \qquad \rho=2, \\[3pt] x=0 \qquad &\text{becomes} \qquad \varphi=\frac{\pi}{2}, \\[3pt] y=x \qquad &\text{becomes} \qquad \varphi=\frac{\pi}{4}, \\[3pt] z=0 \qquad &\text{becomes} \qquad z=0 \\[3pt] z=1 \qquad &\text{becomes} \qquad z=1. \end{align*}\] Therefore \(D\) can be written as \[D = \left\{ (\rho, \varphi,z): 1\leq \rho \leq 2, \frac{\pi}{4} \leq \varphi \leq \frac{\pi}{2}, 0 \leq z \leq 1 \right\}.\]
Calculating the Jacobian, one obtains
Applying Theorem 13.2.1 one has