Chapter 8 Taylor’s Theorem
8.1 Recap of Taylor’s Theorem for \(f(x)\)
Taylor’s Theorem: Let \(f(x)\) be a univariate real-valued function that is infinitely differentiable and let \(a \in \mathbb{R}\). For sufficiently small values of \(h\), one has \[f(a+h) = \sum\limits_{r=0}^{n} \frac{1}{r!} h^{r} f^{(r)}(a) + R_n\] where the remainder \(R_n\) is given by \[R_n = \frac{1}{(n+1)!} h^{n+1} f^{(n+1)}(a+th), \qquad \text{for some } t \in [0,1].\]
Note that \(R_n\) is the next term that would appear in the summation only with \((n+1)^{th}\) derivative of \(f\) evaluated at some unknown value between \(a\) and \(a+h\).
The expression \(\sum\limits_{r=0}^{n} \frac{1}{r!} h^{r} f^{(r)}(a)\) appearing in Taylor’s theorem is known as the \(n^{th}\) Taylor polynomial of \(f\) about \(a\).
Treating \(h\) as a variable, the \(n^{th}\) Taylor polynomial is indeed a polynomial of degree \(n\). Since \(h = x-a\) where \(a\) is fixed, the \(n^{th}\) Taylor polynomial can be thought of as a polynomial in \(x\) of degree \(n\). The idea is that the Taylor polynomials give a polynomial approximation of \(f(x)\) in a neighborhood of \(a\) which in general improves with increasing \(n\).

Let \(n \rightarrow \infty\) in Taylor’s Theorem. If \(R_{n} \rightarrow 0\) and \(h\) is substituted for \(x-a\), then one obtains the Taylor series of \(f\) about \(a\): \[\begin{align*} f(x) &= f(a) + (x-a) f'(a) + \frac{1}{2}(x-a)^2 f''(a) + \ldots + \frac{1}{n!} (x-a)^{n} f^{(n)}(a) + \ldots \\ &= \sum\limits_{r=0}^{\infty} \frac{1}{k!} (x-a)^{r} f^{(r)}(a). \end{align*}\]
Taking \(a=0\) in Definition 8.1.3 recovers the MacClaurin series of \(f(x)\).
8.2 Taylor’s Theorem for \(f(x,y)\)
Taylor’s Theorem extends to multivariate functions. In particular we will study Taylor’s Theorem for a function of two variables.
Taylor’s Theorem: Let \(f(x,y)\) be a real-valued function of two variables that is infinitely differentiable and let \((a,b) \in \mathbb{R}^{2}\). For sufficiently small values of \(h,k\), one has \[f(a+h,b+k) = \sum\limits_{r=0}^{n} \frac{1}{r!} \left. \left( (x-a) \frac{\partial}{\partial x} + (y-b) \frac{\partial}{\partial y} \right)^{r} f(x,y) \right\rvert_{(a,b)} + R_n\] where the remainder \(R_n\) is given by \[R_n = \frac{1}{(n+1)!} \left. \left( h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y} \right)^{n+1} f(x,y) \right\rvert_{(a+th,b+tk)}, \qquad \text{for some } t \in [0,1].\]
Note that the expression \(h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y}\) appearing in Theorem 8.2.1 is an operator that will be applied to \(f(x,y)\). For example
\[\left( h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y} \right) f(x,y) = h \frac{\partial f}{\partial x} + k \frac{\partial f}{\partial y}.\]
The exponent \(r\) of this operator dictates that the operator should be applied \(r\) times. For example
\[\begin{align*}
\left( h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y} \right)^2 f(x,y) &=\left( h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y} \right) \left( h \frac{\partial f}{\partial x} + k \frac{\partial f}{\partial y} \right) \\
&= h^2 \frac{\partial^2 f}{\partial x^2} + 2hk \frac{\partial^2 f}{\partial x \partial y} + k^2 \frac{\partial^2 f}{\partial y^2}.
\end{align*}\]
The result of this operator being applied to \(f(x,y)\) is subsequently evaluated at the point \((a,b)\). This is indicated by the notation \(\rvert_{(a,b)}\).
The term \(R_n\) featuring in Theorem 8.2.1, is the next term that would appear in the summation except for that the \((n+1)^{th}\) partial derivatives of \(f(x,y)\) are evaluated at some unknown point on the straight line between \((a,b)\) and \((a+h,b+k)\).
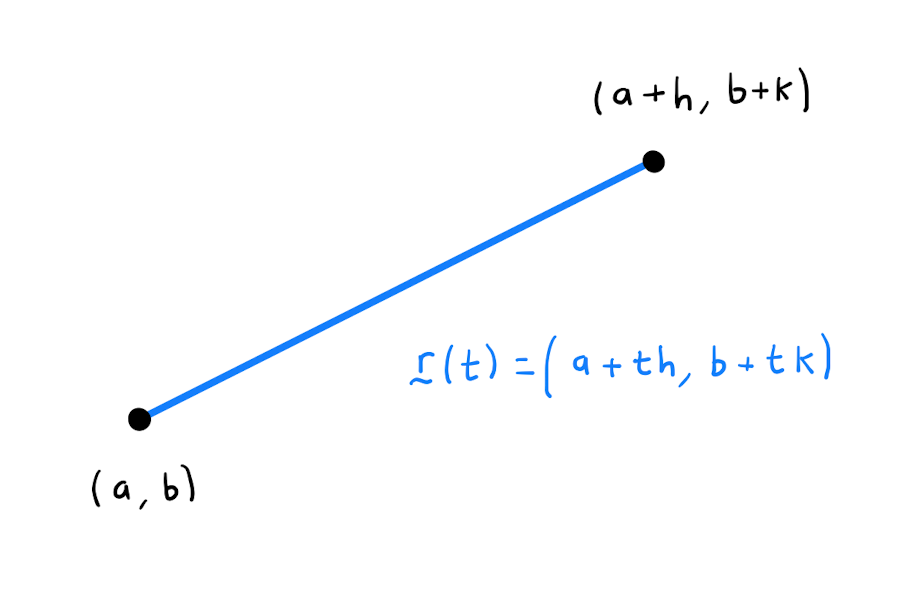
The exact value of \(t\) is not usually known exactly, meaning the value of \(R_n\) is unknown. However an upper bound on \(R_n\) is often possible, meaning that the summation in Theorem 8.2.1 provides an approximation to \(f(x,y)\) with a calculable accuracy.
The expression \(\sum\limits_{r=0}^{n} \frac{1}{r!} \left. \left( h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y} \right)^{r} f(x,y) \right\rvert_{(a,b)}\) appearing in Taylor’s theorem is known as the \(n^{th}\) Taylor polynomial of \(f(x,y)\) about \((a,b)\).
Treating \(h\) and \(k\) as variables, the \(n^{th}\) Taylor polynomial is indeed a polynomial of degree \(n\). Since \(h = x-a, k=y-b\) where \((a,b)\) is fixed, the \(n^{th}\) Taylor polynomial can be thought of as a polynomial in variables \(x,y\) of degree \(n\). The idea is that the Taylor polynomials give a polynomial approximation of \(f(x,y)\) in a neighborhood of \((a,b)\) which in general improves with increasing \(n\).
The first few terms of the sum in Taylor’s theorm grouped by degree are given explicitly by \[\begin{align*} f(a+h,b+k) = f(a,b) + \bigg( &h f_x(a,b) + k f_y(a,b) \bigg) \\ &+ \frac{1}{2} \bigg(h^2 f_{xx}(a,b) + 2hk f_{xy}(a,b) + k^2 f_{yy}(a,b) \bigg) + \ldots \end{align*}\]
Let \(n \rightarrow \infty\) in Taylor’s Theorem. If \(R_{n} \rightarrow 0\) and \(x-a\), \(y-b\) are substituted in for \(h, k\) respectively, then one obtains the Taylor series of \(f\) about \((a,b)\): \[\begin{align*} f(x,y) &= f(a,b) + (x-a) f_{x}(a,b) + (y-b) f_y(a,b) + \frac{1}{2}(x-a)^2 f_{xx}(a,b) + \ldots \\ &= \sum\limits_{r=0}^{\infty} \frac{1}{r!} \left. \left( h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y} \right)^{r} f(x,y) \right\rvert_{(a,b)}. \end{align*}\]
8.3 Linear Approximation using Taylor’s Theorem
Having established that the \(n^{th}\) Taylor polynomial from Definition 8.2.2 gives a degree \(n\) polynomial approximation of \(f\) in a neighbourhood of \((a,b)\), by setting \(n=1\) one obtains a linear approximation of \(f(x,y)\) near \((a,b)\). Specifically \[f(x,y) \approx f(a,b) + (x-a) f_{x}(a,b) + (y-b) f_y (a,b) = L(x,y).\]
Note \(z=L(x,y)\) is linear in \(x\) and \(y\) so is a plane. Specifically this is the tangent plane to the surface \(z=f(x,y)\) at \((a,b)\).
Indeed this linear approximation is one we have already seen in the course. This approximation is essentially the same as the small changes formula \(\Delta f = \frac{\partial f}{\partial x} \Delta x + \frac{\partial f}{\partial y} \Delta y\) that we saw in Section 5.1.
Find the linear approximation to the function \(f(x,y)= \frac{1}{2}xy + 2\) near \((x,y)=(2,1)\).
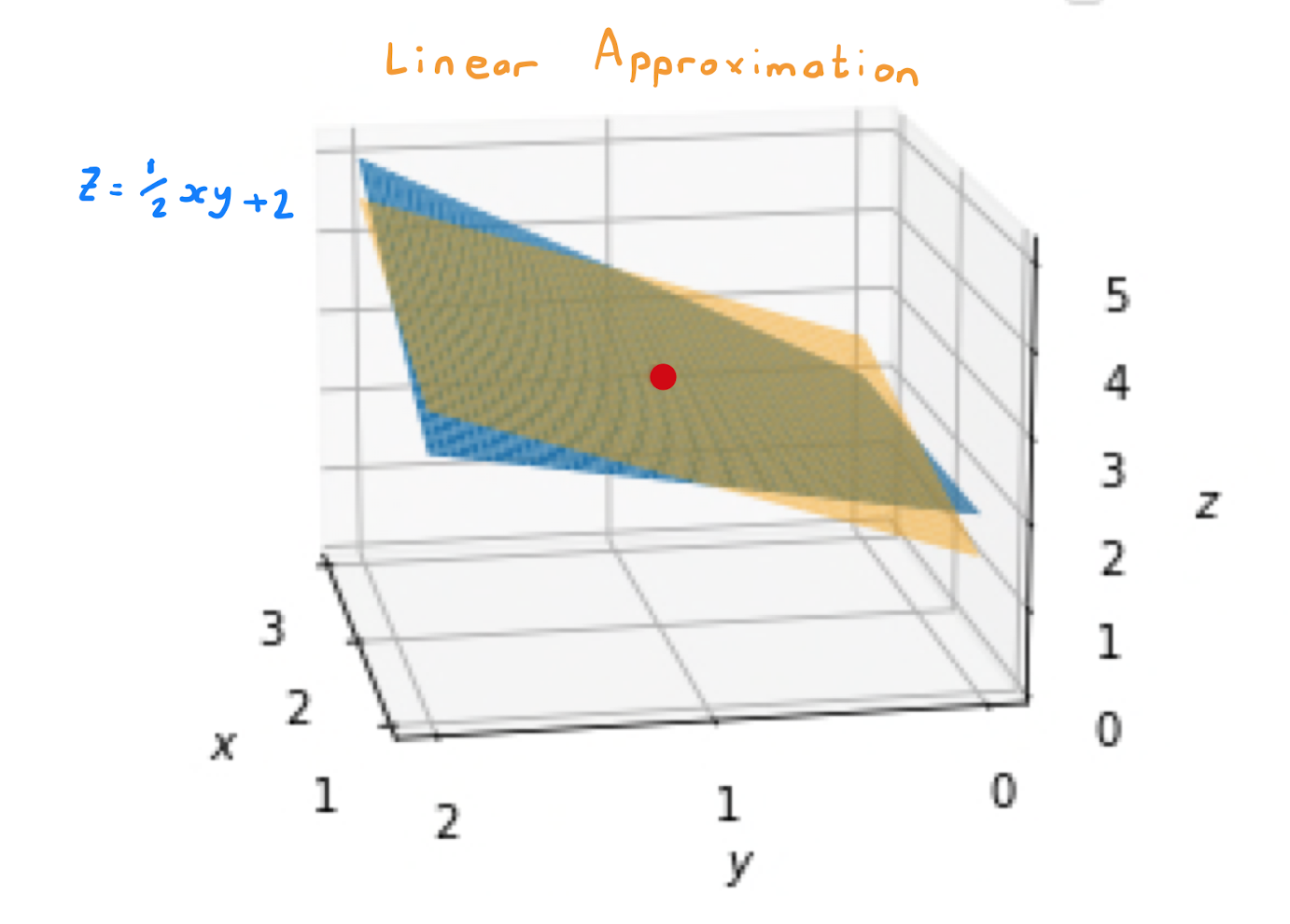
The linear approximation of \(f\) obtained through Taylor’s theorem, setting \(a=2, b=1\), is \[f(x,y) \approx L(x,y) = f(2,1) + (x-2) f_x (2,1) + (y-1) f_y (2,1).\] Calculate that \[\begin{align*} &f(x,y) = \frac{1}{2}xy +2, \qquad \qquad &f(2,1) = 3, \\ &f_x(x,y) = \frac{1}{2}y, \qquad \qquad &f_x(2,1) = \frac{1}{2}, \\ &f_y(x,y) = \frac{1}{2}x, \qquad \qquad &f_y(2,1) = 1. \end{align*}\] Therefore the required linear approximation is \[L(x,y) = 3 +\frac{1}{2} \cdot (x-2) + 1 \cdot (y-1) = \frac{1}{2}x + y+1.\]
\(L(x,y)\) has the following properties:
\(L(a,b) = f(a,b)\);
\(L_x(a,b) = f_x(a,b)\);
\(L_y(a,b) = f_y(a,b)\).
Prove each of the statements in Lemma 8.3.2.
8.4 Quadratic Approximation using Taylor’s Theorem
Similarly to Section 8.3, setting \(n=2\) in the Taylor polynomial of Definition 8.2.2 gives a quadratic approximation of \(f\) in a neighbourhood of \((a,b)\). Specifically \[\begin{align*} f(x,y) \approx f(a,b) + &(x-a) f_x(a,b) + (y-b) f_y(a,b) \\ &+ \frac{1}{2} \Big[ (x-a)^2 f_{xx}(a,b) + 2(x-a)(y-b) f_{xy}(a,b) + (y-b)^2 f_{yy}(a,b) \Big] \\ =Q(x,y).& \end{align*}\]
Find the quadratic approximation to the function \(f(x,y)= e^{x^2 +y}\) in a neighbourhood of \((0,0)\).
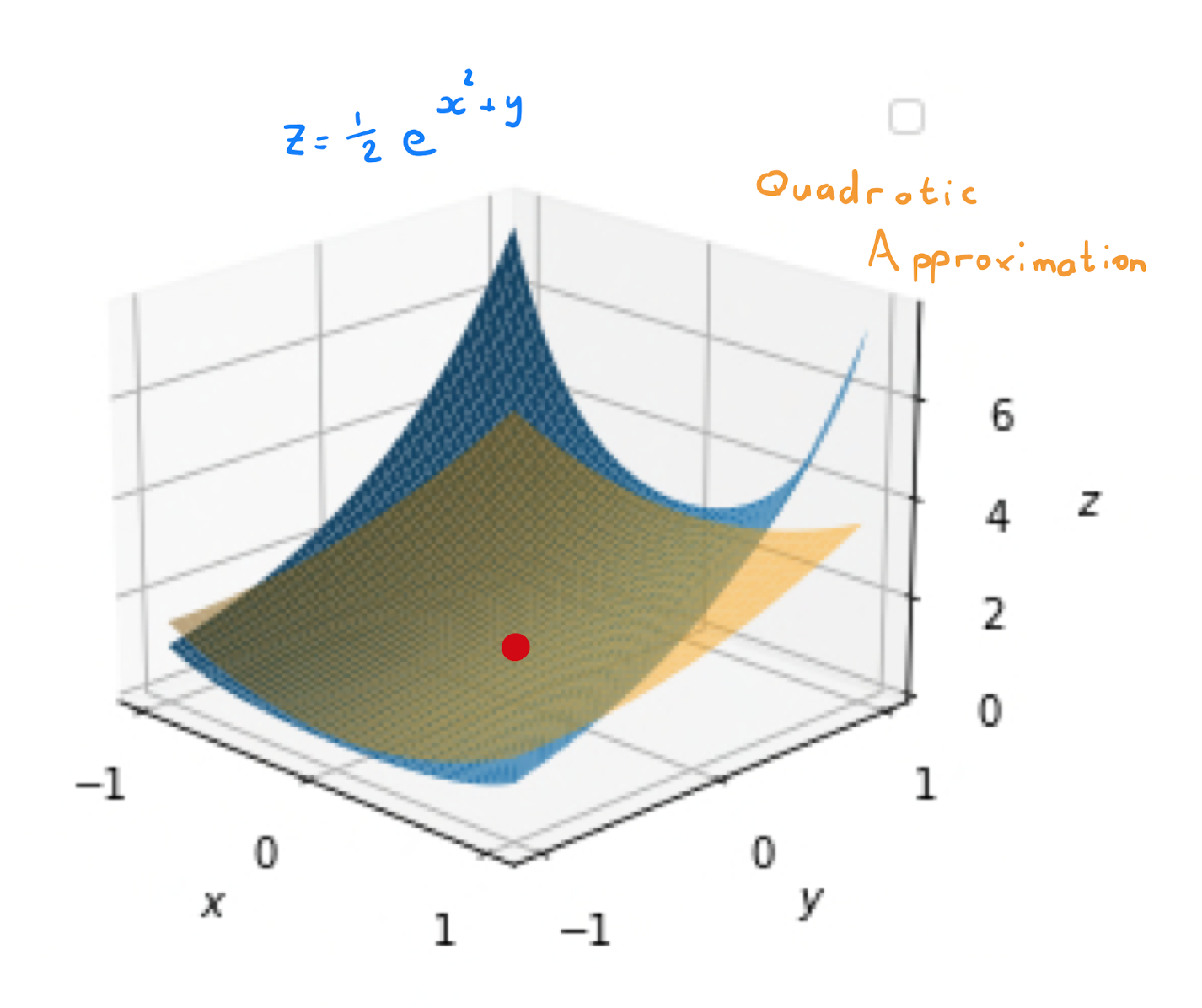
The quadratic approximation of \(f\) obtained through Taylor’s theorem, setting \(a=0, b=0\), is \[\begin{align*} f(x,y) &\approx Q(x,y) \\ &= f(0,0) + xf_x (0,0) + y f_y (0,0) + \frac{1}{2} \Big[ x^2 f_{xx}(0,0) + 2xy f_{xy}(0,0) + f_{yy}(0,0) \Big] \end{align*}\]
Calculate that
Therefore the required quadratic approximation is given by
Find the quadratic approximation \(Q(x,y)\) to the function \(f(x,y)= \frac{1}{2}xy + 2\) near \((x,y)=(2,1)\). What do you notice about the answer?
\(Q(x,y)\) has the following properties:
\(Q(a,b) = f(a,b)\);
\(Q_x(a,b) = f_x(a,b)\);
\(Q_y(a,b) = f_y(a,b)\);
\(Q_{xx}(a,b) = f_{xx}(a,b)\);
\(Q_{xy}(a,b) = f_{xy}(a,b)\);
\(Q_{yy}(a,b) = f_{yy}(a,b)\).
Prove each of the statements in Lemma 8.4.2.