Chapter 6 Chain Rule

6.1 Definition

Consider univariate functions \(y=y(x)\) and \(x=x(t)\). Note a change in \(t\) will result in a change in \(x\), which subsequently results in a change in \(y\). How does \(y\) change with \(t\)? One has the well known formula: \[\frac{dy}{dt} = \frac{dy}{dx} \frac{dx}{dt}.\] How does this translate to the multivariate case? Consider a function \(z=z(x,y)\), where \(x=x(u,v)\) and \(y=y(u,v)\). As either \(u\) or \(v\) change both \(x\) and \(y\) will change, and subsequently \(z\) will change. How does \(z\) change with \(u\), and how does \(z\) change with \(v\)? It would be theoretically possible to calculate this by a substitution of \(x=x(u,v)\) and \(y=y(u,v)\) into \(z=z(x,y)\), but for most functions this will a tedious computation.

More generally consider the function \(z = z(x_1,x_2 \ldots , x_n)\), which is dependent on \(n\) variables. Each of the \(x_j\) is a function of \(k\) variables, that is, \(x_j = x_j (t_1, t_2, \ldots, t_k )\). A variation in any of the \(t_i\), results in a change in each of the \(x_i\), which subsequently changes the value of \(z\). How does \(z\) change with respect to change in each of the \(t_i\).

Chain Rule. Given \(z = z(x_1,x_2 \ldots , x_n)\) where \(x_i = x_i (t_1, t_2, \ldots, t_k )\), it follows that \[\frac{\partial z}{\partial t_i} = \sum\limits_{j=1}^{n} \frac{\partial z}{\partial x_j} \frac{\partial x_j}{\partial t_i}.\]

Note that the derivatives that appear on the right hand side of the Chain Rule will be routine to compute from the expressions \(z = z(x_1,x_2 \ldots , x_n)\) and \(x_i = x_i (t_1, t_2, \ldots, t_k )\).

Consider \(z=z(x,y)\) where \(x=x(u,v)\) and \(y=y(u,v)\) as above. By the chain rule \[\begin{align*} \frac{\partial z}{\partial u} &= \frac{\partial z}{\partial x} \frac{\partial x}{\partial u} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial u}, \\ \frac{\partial z}{\partial v} &= \frac{\partial z}{\partial x} \frac{\partial x}{\partial v} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial v}. \end{align*}\]

Consider \(u=u(x,y,z)\) where \(x=x(\alpha,\beta), y=y(\alpha,\beta)\) and \(z=z(\alpha,\beta)\). By the chain rule \[ \frac{\partial u}{\partial \alpha} = \frac{\partial u}{\partial x} \frac{\partial x}{\partial \alpha} + \frac{\partial u}{\partial y} \frac{\partial y}{\partial \alpha} + \frac{\partial u}{\partial z} \frac{\partial z}{\partial \alpha}.\]

Consider \(u=u(x,y)\) where \(x=x(\alpha,\beta, \gamma)\) and \(y=y(\alpha,\beta, \gamma)\). By the chain rule \[ \frac{\partial u}{\partial \beta} = \frac{\partial u}{\partial x} \frac{\partial x}{\partial \beta} + \frac{\partial u}{\partial y} \frac{\partial y}{\partial \beta}.\]

Calculate \(\frac{\partial u}{\partial \beta}\) in Example 6.1.3, and \(\frac{\partial u}{\partial \gamma}\) in Example 6.1.4.

Find the derivative of \(w = \frac{1}{2} xy+ 2\) with respect to \(t\) along the path \(x= \cos t\), \(y = \sin t\). What is the value of the derivative at \(t = \frac{\pi}{2}\)?

The question has a nice geometrical interpretation:

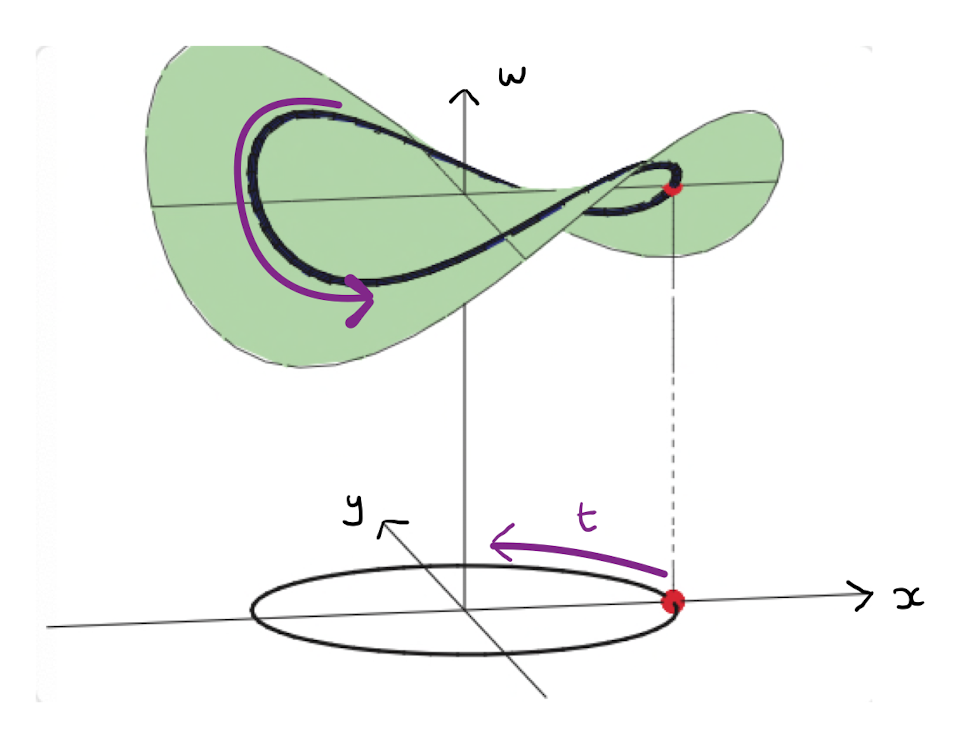
Note that \(w\) is a function of \(x\) and \(y\), while \(x\) and \(y\) are both functions of \(t\). Therefore by the Chain rule: \[\begin{align*} \frac{\partial w}{\partial t} &= \frac{\partial w}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial w}{\partial y} \frac{\partial y}{\partial t} \\ &= \frac{1}{2} y \cdot \left( - \sin t \right) + \frac{1}{2} x \cdot \cos t \\ &= - \frac{1}{2} \sin^{2} t + \frac{1}{2} \cos^{2} t \\ &= \frac{1}{2} \cos (2t). \end{align*}\] At \(t = \frac{\pi}{2}\), evaluate: \[\frac{\partial w}{\partial t} \left( \frac{\pi}{2} \right) = - \frac{1}{2}.\]

6.2 Implicit Differentiation

Suppose a function \(y(x)\) is given implicitly, that is, \(y(x)\) satisfies some equation \(F(x,y) =0\). One can deduce a simple formula for \(\frac{d y}{d x}\) via the Chain Rule.

Given \(y(x)\) satisfying \(F(x,y) =0\), then \[\frac{d y}{d x} = - \frac{F_x}{F_y},\] if \(F_y \neq 0\).

Let \(w = F(x,y)\), so \(w\) is a function of \(x\) and \(y\). Now \(y\) is a function of \(x\), and trivially so is \(x\) itself. Therefore by the Chain Rule: \[\begin{align*} \frac{dw}{dx} &= \frac{\partial w}{\partial x} \frac{\partial x}{\partial x} + \frac{\partial w}{\partial y} \frac{d y}{d x} \\ &= \frac{\partial F}{\partial x} \cdot 1 + \frac{\partial F}{\partial y} \frac{d y}{d x} \\ &= \frac{\partial F}{\partial x} + \frac{\partial F}{\partial y} \frac{d y}{d x}. \end{align*}\]

Since \(w = F(x,y)=0\) by definition, it follows that \(w\) is constant and so \(\frac{dw}{dx}=0\). By substitution \[\begin{align*} 0 &= \frac{\partial F}{\partial x} + \frac{\partial F}{\partial y} \frac{d y}{d x} \\[6pt] \implies \qquad \frac{d y}{d x} &= - \frac{\frac{\partial F}{\partial x}}{ \frac{\partial F}{\partial y}} \\[3pt] &= - \frac{F_x}{F_y} \end{align*}\]

provided \(F_y \neq 0\).

Find \(\frac{dy}{dx}\) where \(y^2 -x^2 - \sin (xy) =0\).

Define \(F(x,y) = y^2 -x^2 - \sin (xy)\). Calculate that:

\[\begin{align*} F_x &= -2x - y \cos (xy), \\ F_y &= 2y - x \cos (xy). \end{align*}\]

Therefore by Lemma 6.2.1, provided \(F_y \neq 0\):

\[\frac{dy}{dx} = \frac{2x+y \cos (xy)}{2y - x \cos (xy)}.\]

6.3 Transforming Partial Differential Equations

In the Autumn term, we saw how to solve certain collections of ordinary differential equations (ODEs), that is equations that impose conditions on the derivatives of a univariate function. A partial differential equation (PDE), is an equation that imposes a condition on the partial derivatives of a multivariate function. The study of PDEs and their solutions is a deep and active area of research which can be further learnt about in the module MATH2012: Modelling with Differential Equations.

The one-dimensional wave equation for \(u(x,t)\) is the PDE

\[\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2},\]

where \(c>0\) is some constant.

The wave equation occurs frequently in natural phenonmenon:

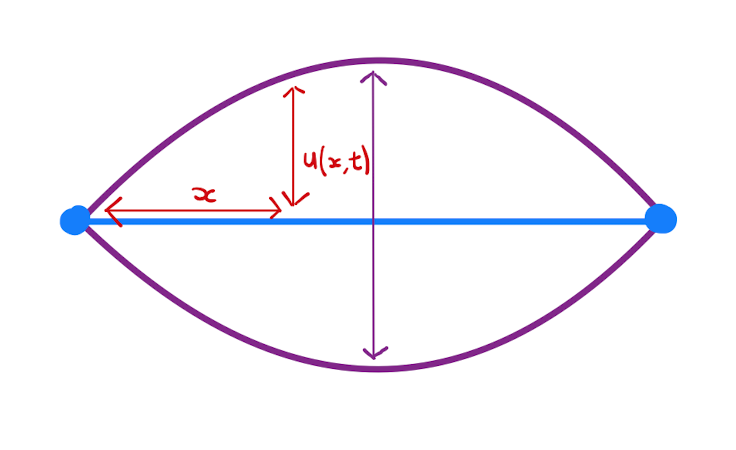
• Consider a horizontal vibrating string that is fixed at both ends. Let \(t\) represent time, \(x\) represent a distance along the string, and \(u(x,t)\) be the vertical displacement of the point \(x\) at time \(t\). Then \(u(x,t)\) satisfies the wave equation.

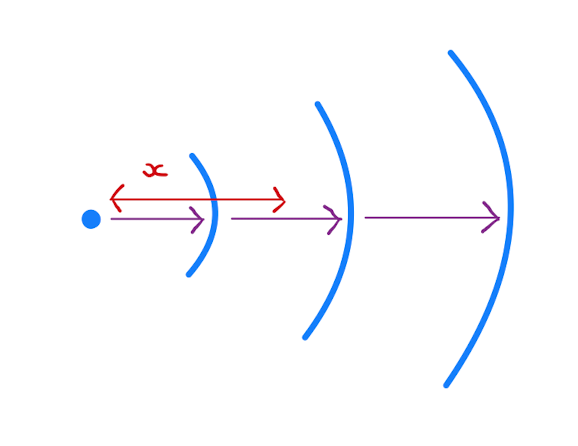
• Consider a sound wave emanating from a point source along a line. Let \(t\) represent time, \(x\) represent a point at displacement \(x\) from the source, and \(u(x,t)\) be the perturbation in air density at the point \(x\) at time \(t\). Then \(u(x,t)\) satisfies the wave equation.

• Consider a wave of water travelling along a cross section of a body of water. Let \(t\) represent time, \(x\) represent a point along the cross section, and \(u(x,t)\) be the sea level at the point \(x\) at time \(t\). Then \(u(x,t)\) satisfies the wave equation.

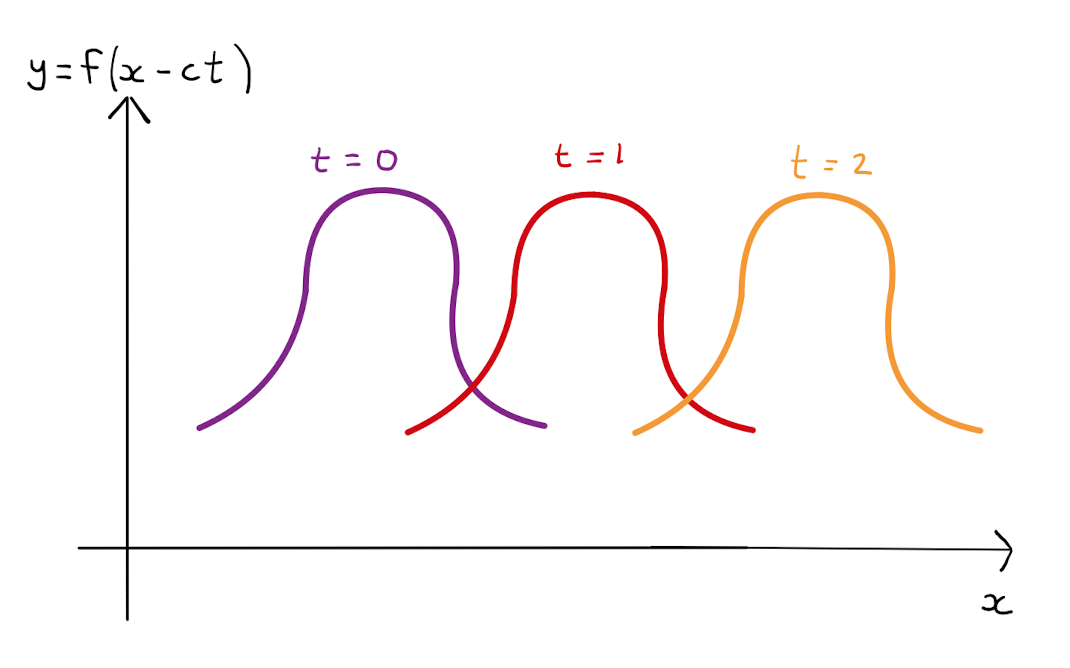
The solution \(u(x,t)\) to the wave equation \(u_{tt} = c^2 u_{xx}\) is of the form \[u(x,t)=f(x-ct) + g(x+ct)\] where \(f\) and \(g\) are some general functions.

Set \[\alpha = \alpha(x,t) = x-ct, \qquad \text{and} \qquad \beta = \beta(x,t) = x+ct.\] The plan is to interpret the wave equation in terms of \(\alpha, \beta\) rather than \(x,t\). The differential equation will then be solved in terms of \(\alpha,\beta\) before the solution is converted back to in terms of \(x,t\).

Calculate that \[x = \frac{\alpha+\beta}{2}, \qquad \text{and} \qquad t = \frac{\beta - \alpha}{2c}.\] By substitution, one could think of \(u\) as a function of \(\alpha\) and \(\beta\). Therefore by the Chain Rule \[\begin{align*} u_x &= \frac{\partial u}{\partial x} \\ &= \frac{\partial u}{\partial \alpha} \frac{\partial \alpha}{\partial x} + \frac{\partial u}{\partial \beta} \frac{\partial \beta}{\partial x} \\ &= \frac{\partial u}{\partial \alpha} \cdot 1 + \frac{\partial u}{\partial \beta} \cdot 1 \\ &= \frac{\partial u}{\partial \alpha} + \frac{\partial u}{\partial \beta} \\ &= u_\alpha + u_\beta. \end{align*}\]

Note that this equation holds for any function \(u\). Therefore it this setting it is correct to state there is an equivalence of operators: \[\frac{\partial}{\partial x} = \frac{\partial}{\partial \alpha} + \frac{\partial}{\partial \beta},\] that is, differentiating a function with respect to \(x\) is the same as the sum of the derivative with respect to \(\alpha\) and the derivative with respect to \(\beta\).

Similarly the Chain Rule gives \[u_t = \frac{\partial u}{\partial t} = -c \frac{\partial u}{\partial \alpha} + c \frac{\partial u}{\partial \beta} = -c u_\alpha + c u_\beta,\] and in terms of operators \[\frac{\partial}{\partial t} = -c \frac{\partial}{\partial \alpha} + c \frac{\partial}{\partial \beta}\] Now calculating the second order derivatives of \(u\) that appear in the PDE, one has

\[\begin{align*} u_{xx} &= \frac{\partial}{\partial x} u_x \\ &= \left( \frac{\partial}{\partial \alpha} + \frac{\partial}{\partial \beta} \right) \left( u_\alpha + u_\beta \right) \\ &= u_{\alpha \alpha} + u_{\beta \alpha} + u_{\alpha \beta} + u_{\beta \beta} \\ &= u_{\alpha \alpha} + 2 u_{\beta \alpha} + u_{\beta \beta} \\[5pt] u_{tt} &= \frac{\partial}{\partial t} u_t \\ &= \left( -c \frac{\partial}{\partial \alpha} + c \frac{\partial}{\partial \beta} \right) \left( -c u_\alpha + c u_\beta \right) \\ &= c^2 u_{\alpha \alpha} -c^2 u_{\beta \alpha} -c^2 u_{\alpha \beta} + c^2 u_{\beta \beta} \\ &= c^2 u_{\alpha \alpha} - 2 c^2 u_{\alpha \beta} + c^2 u_{\beta \beta} \end{align*}\]

By substitution into the wave equation

\[\begin{align*} 0 &= u_{tt} - c^2 u_{xx} \\ &= \Big( c^2 u_{\alpha \alpha} - 2 c^2 u_{\alpha \beta} + c^2 u_{\beta \beta} \Big) - c^2 \Big( u_{\alpha \alpha} + 2 u_{\beta \alpha} + u_{\beta \beta} \Big) \\ &= -4 c^2 u_{\alpha \beta} \\ \iff \qquad u_{\alpha \beta} &= 0 \end{align*}\]

Solving this new differential equation:

\[\begin{align*} u_{\alpha \beta} &= 0 \\ \int u_{\alpha \beta} \,d\beta &= \int 0 \,d\beta \\ u_{\alpha} &= c(\alpha) \\ \int u_{\alpha} \,d\alpha &= \int c(\alpha) \,d\alpha \\ u &= f(\alpha) + g(\beta), \qquad \text{where } \frac{df}{d \alpha} = c. \end{align*}\]

Therefore

\[u(x,t) = f(x-ct) + g(x+ct)\]

is the general solution to the wave equation.

Physically the variable \(t\) represents time, and the variable \(x\) represents some sort of spatial displacement in a one-dimensional space. It follows that the solution to the wave equation is a combination of two general waves moving in opposite directions along the \(x\)-axis with speed \(c\).