Chapter 7 Applications to Surfaces
On a curve in two-dimensional space \(\mathbb{R}^{2}\), there is:
a tangent line;
a normal line.
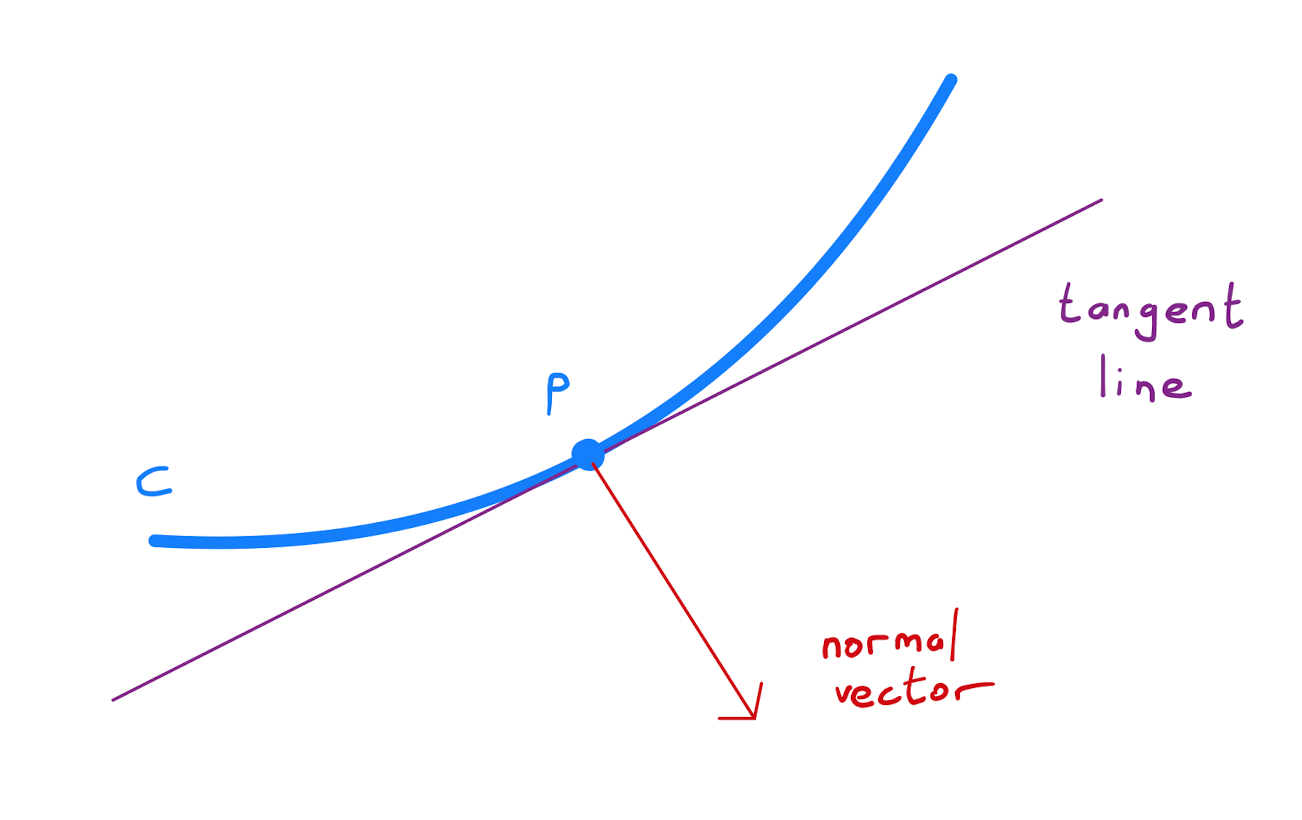
What are the corresponding features of a surface in three-dimensional space \(\mathbb{R}^{3}\)?
7.1 Surfaces in Cartesian Coordinates
All surfaces considered in this section are assumed to be described as the set of points in \(\mathbb{R}^{3}\) that satisfy some equation of the form \[F(x,y,z)=0.\]
The grad of \(F\) is the vector \(\nabla F = \left( \frac{\partial F}{\partial x}, \frac{\partial F}{\partial y}, \frac{\partial F}{\partial z} \right)\).
The symbol \(\nabla\) is called a nabla or a del.
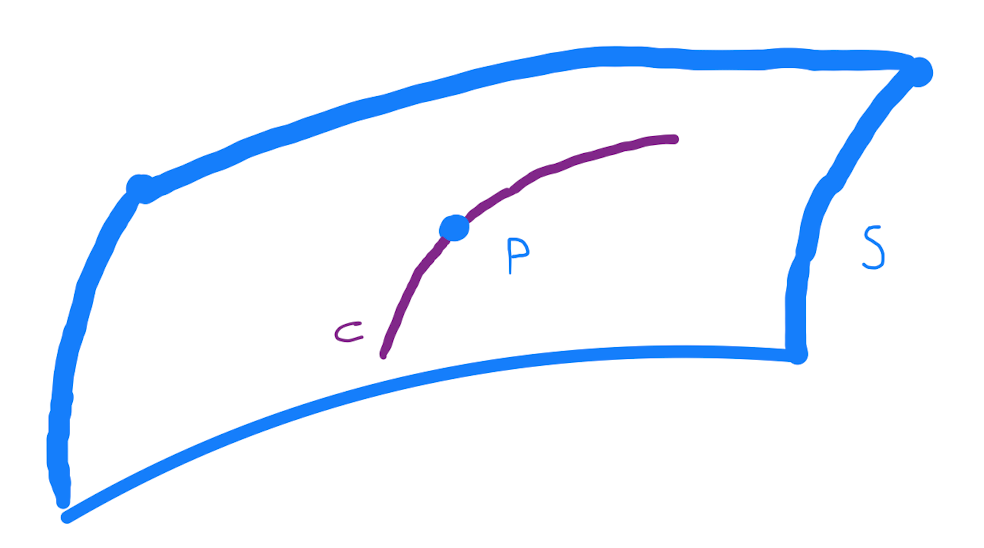
Let \(S\) be a surface described by \(F(x,y,z)=0\), and let \(P\) be a point on \(S\). Then \(\nabla F (P)\) is a normal vector to \(S\) at \(P\).
let \(C\) be a curve that passes through \(P\), and lies entirely on \(S\).
Consider a parametrisation \(\mathbf{r}(t) = \big( x(t), y(t), z(t) \big)\) of \(C\). The tangent line to \(P\) at \(C\) is given by \(\frac{d \mathbf{r}}{dt} = \big( \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \big)\). Since \(C\) lies on \(S\), it follows that \(F \big( x(t), y(t), z(t) \big) =0\), for all \(t\). Hence \[\frac{dF}{dt}\big( x(t), y(t), z(t) \big) =0, \qquad \text{for all } t.\] By the Chain Rule \[\begin{align*} \frac{dF}{dt} &= \frac{dF}{dx} \frac{dx}{dt} + \frac{dF}{dy} \frac{dy}{dt} + \frac{dF}{dz} \frac{dz}{dt} \\[5pt] &= \left( \frac{dF}{dx}, \frac{dF}{dy}, \frac{dF}{dz} \right) \cdot \left( \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \right) \\[5pt] &= \nabla F \cdot \frac{d \mathbf{r}}{dt} \end{align*}\]
Provided \(\nabla F \neq \mathbf{0}\) and \(\frac{d \mathbf{r}}{dt}\neq \mathbf{0}\), then \(\nabla F\) is perpendicular to the tangent to the curve \(C\) at \(P\).
This discussion applies to all such curves on \(S\) through \(P\). Therefore \(\nabla F\) is perpendicular to all tangent vectors to \(S\) at \(P\), and is a normal vector to \(S\).

The unique plane through \(P\) that is perpendicular to \(\nabla F\) is the tangent plane to \(S\) at \(P\).

Find a normal vector and the tangent plane to the surface \(z = x + 2y - \frac{1}{2} \left( x^2 + y^2 \right)\) at the point \(P\) where \((x,y)= \left( \frac{5}{4}, \frac{5}{2} \right)\).
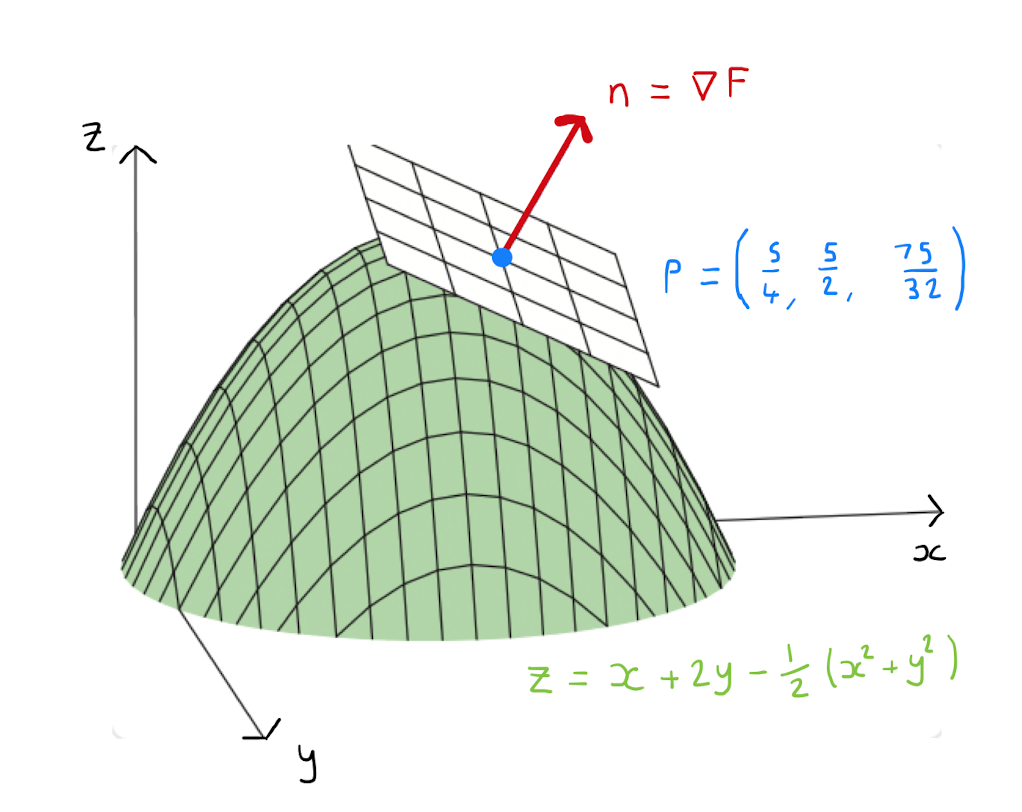
When \((x,y)= \left( \frac{5}{4}, \frac{5}{2} \right)\), calculate the value of \(z\):
Define \(F(x,y,z) = z - x - 2y + \frac{1}{2} \left( x^2 + y^2 \right)\). The surface \(S\) is \(F(x,y,z)=0\). Calculate
Therefore \(\nabla F = \left( -1+x, -2+y, 1 \right)\). Evaluating \(\nabla F\) at \(x= \frac{5}{4}, y = \frac{5}{2}, z= \frac{75}{32}\) shows that the normal to \(S\) at \(P\) is \(\left( \frac{1}{4}, \frac{1}{2}, 1 \right)\). The tangent plane is all the points satisfying
7.2 Surfaces in Parametric Coordinates
Alternatively one can consider a surface \(S\) given in parametric form as discussed in Section 2.4.
Let \(S\) be a surface defined by \(\mathbf{r}(u,v)\) for a set of values of the parameters \(u\), \(v\), and further that \(P = \mathbf{r}(u_0,v_0)\) is a point on \(S\). Then the normal vector to \(S\) at \(P\) is given by \(\mathbf{r}_{u} \times \mathbf{r}_v\).
By fixing the parameter \(u=u_0\) while allowing \(v\) to vary describes a curve \(C_1\) that both lies on the surface \(S\), and passes through \(P\). Similarly fixing the parameter \(v=v_0\) while allowing \(u\) to vary describes another curve \(C_2\) that lies on the surface \(S\) and passes through \(P\).

The tangent vectors to \(C_1\) and \(C_2\) at \(P\) are given respectively by \(\frac{\partial \mathbf{r}}{\partial u}(P) = \mathbf{r}_{u}(P)\) and \(\frac{\partial \mathbf{r}}{\partial v}(P) = \mathbf{r}_{v}(P)\). Hence provided that these tangent vectors exist and are not parallel, the tangent plane to \(S\) at \(P\) is uniquely determined by the point \(P\) and the direction vectors \(\mathbf{r}_u\) and \(\mathbf{r}_u\). It follows from the geometric interpretation of the cross product that \(\mathbf{r}_u \times \mathbf{r}_v\) is a normal vector to \(S\) at \(P\).
Having a simple formula for the normal of a parametric surface at a point, also provides a simple method by which to calculate the tangent plane of a parametric surface at a point.
Find the normal vector at a general point on the parametric surface \(S\) described by
\[\mathbf{r}(u,v) = \big( \text{sech} (u) \cos (v), \text{sech}(u) \sin (v), u - \text{tanh} (u) \big), \qquad \text{where } u \in (- \infty, \infty), v \in [0, 2 \pi).\]
Further find the tangent plane to \(S\) at the point \(P = \mathbf{r} \left(\frac{3}{2},\frac{\pi}{2} \right).\)

Calculate that \[\begin{align*} \mathbf{r}_u &= \big( - \text{sech} (u) \text{tanh} (u) \cos (v), - \text{sech} (u) \text{tanh}(u) \sin (v), 1 - \text{sech}^{2} (u) \big) \\ &= - \text{sech} (u) \text{tanh}(u) \Big( \cos (v), \sin (v), - \text{sinh}(u) \Big), \end{align*}\] and \[\begin{align*} \mathbf{r}_v &= \Big( -\text{sech} (u) \sin (v), \text{sech}(u) \cos (v), 0 \big) \\ &= \text{sech}(u) \Big( - \sin (v), \cos (v), 0 \Big) \end{align*}\] The scalars can be ignored since we are only interested in the direction of a normal vector. Therefore a normal vector \(\mathbf{N}\) at a general point of \(S\) is given by \[\begin{align*} \mathbf{N}(u,v) &= \mathbf{r}_u \times \mathbf{r}_v \\[9pt] &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \cos (v) & \sin (v) & - \text{sinh} (u) \\ -\sin (v) & \cos (v) & 0 \end{vmatrix} \\[9pt] &= \Big( \text{sinh} (u) \cos (v), \text{sinh} (u) \sin (v), 1 \Big). \end{align*}\]
The point \(P\) has position vector
and normal vector
Therefore the tangent plane at \(P\) has equation
The surface appearing in Example 7.2.2 is known as the psuedosphere.