Chapter 5 Small changes and Differentials

5.1 Small Changes

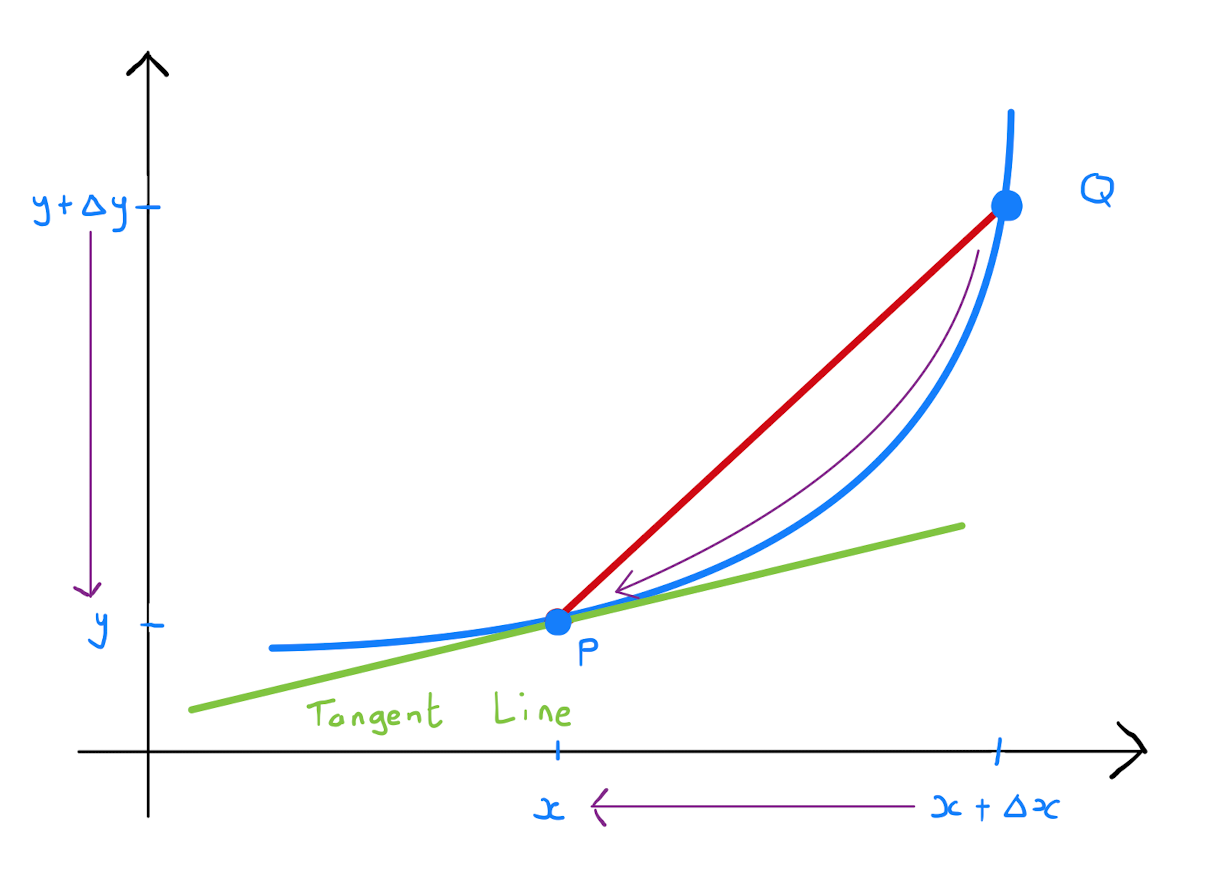
Consider a univariate function $y=y(x)$. Suppose that the variable $x$ from a fixed value undergoes some small increase $\Delta x$. Subsequently, as the dependent variable, there will be some small change in $y$, denoted $\Delta y$. One asks how the change $\Delta y$ can be expressed in terms of $\Delta x$.

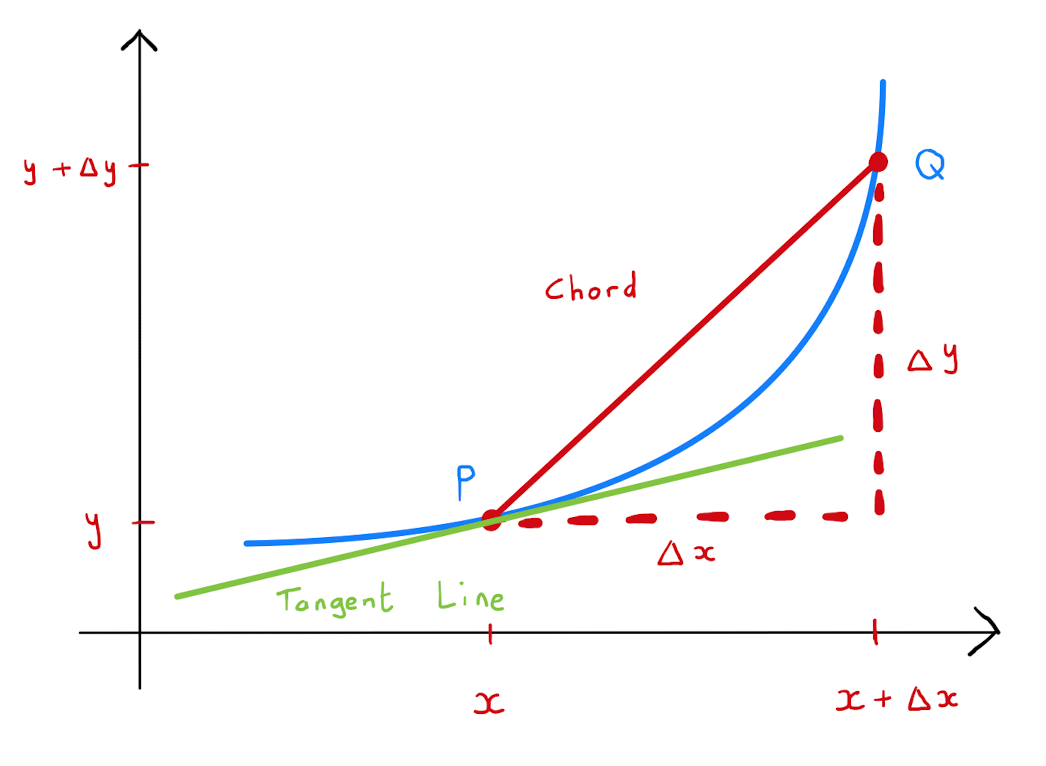
The ratio of $\Delta y$ to $\Delta x$ is equal to the gradient of the chord between the points $P=(x,y)$ and $Q=(x+\Delta x, y+ \Delta y)$. Provided that $\Delta x$ is sufficiently small, this chord is ‘close’ to lying on the tangent line at $P$. Specifically the gradient of the chord $PQ$ can be approximated by the gradient of the tangent line, which is $\frac{d y}{dx}$. Written mathematically: $$\begin{align*} \frac{\Delta y}{\Delta x} &= \text{gradient of chord } PQ \\ &\approx \text{gradient of tangent line at } P \\ &= \frac{dy}{dx} \end{align*}$$ Rearranging one concludes that the small changes $\Delta x$ and $\Delta y$ are related by $$\Delta y \approx \frac{dy}{dx} \Delta x.$$

How is this analysis replicated in the case of an implicit function of two variables $z=z(x,y)$? Well $\Delta z$ will be given by the difference between $z(x,y)$ and $z(x+\Delta x, y+ \Delta y)$. To investigate this quantity consider the parallogram on the surface $z = z(x,y)$ whose vertices are given by the points above $(x,y),(x+\Delta x, y),(x, y+ \Delta y)$ and $(x+\Delta x, y+ \Delta y)$.

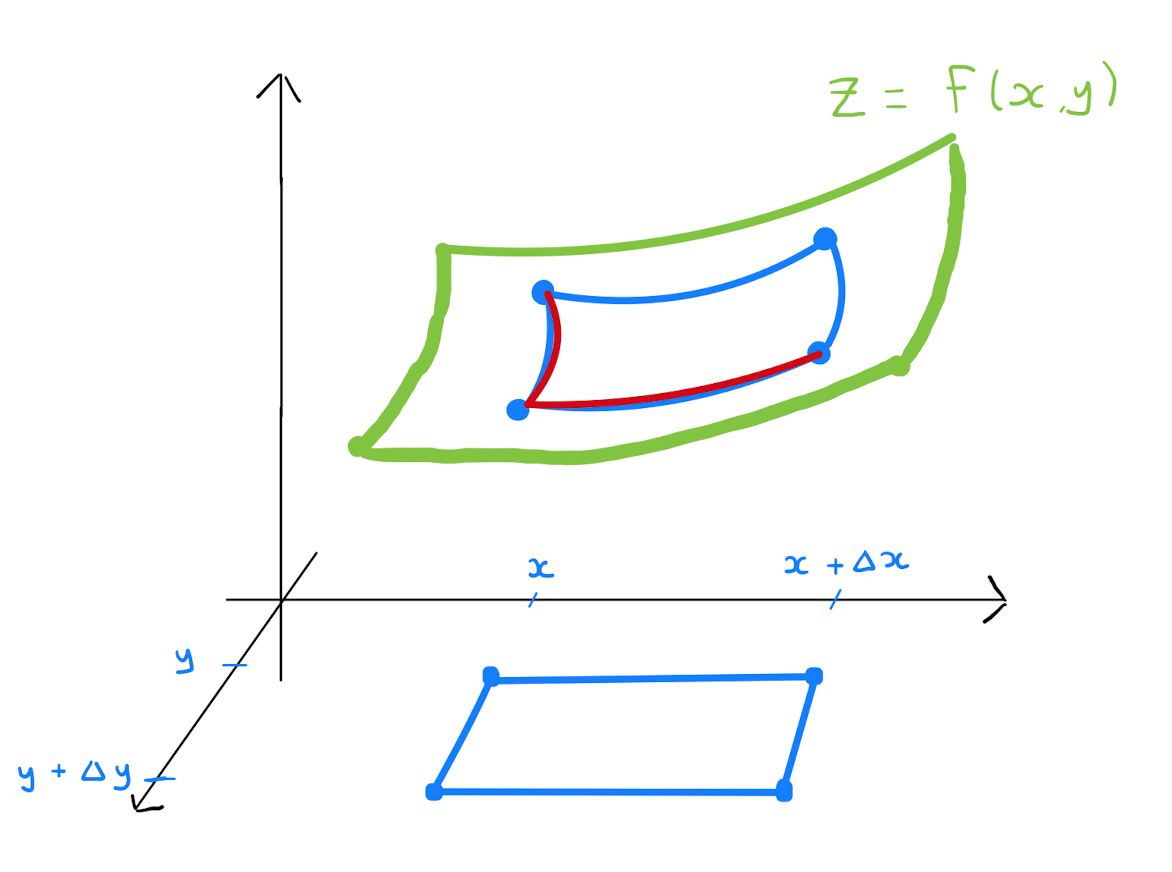
Decomposing the expression for $\Delta z$: $$\begin{align*} \Delta z &= z(x+\Delta x, y+ \Delta y) - z(x,y) \\ &= \Big( z(x+\Delta x, y+ \Delta y) - z(x+\Delta x, y) \Big) + \Big( z(x+\Delta x, y) - z(x, y) \Big). \end{align*}$$ Each bracket represents a change in the dependent variable $z$ as only one of the independent variables is allowed to vary. When studying the term $z(x+\Delta x, y) - z(x, y)$, one can treat the $y$ variable as a fixed constant, and treat $z$ as a function in the single variable $x$.

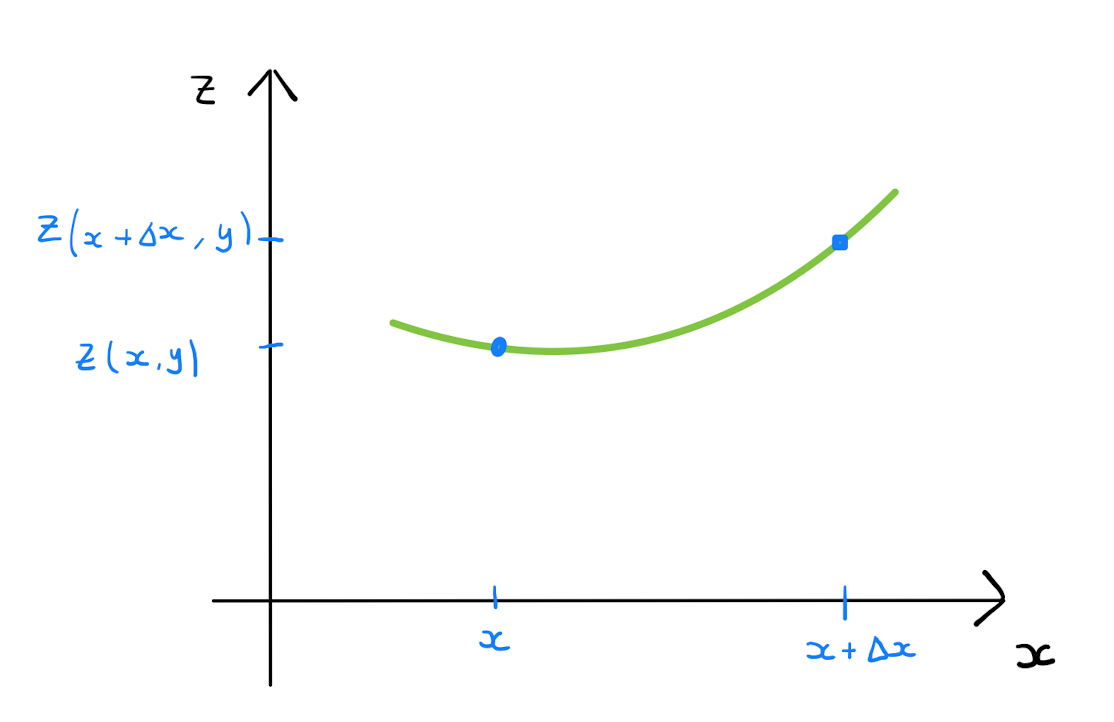
Applying the theory of small changes for univariate functions here gives $$z(x+\Delta x, y) - z(x, y) \approx \Delta x \frac{\partial z}{\partial x}.$$

Similarly the expression $z(x+\Delta x, y+ \Delta y) - z(x+\Delta x, y)$ lends itself to thinking of $z$ as a univariate function. However before doing so, note that since $\Delta x$ is sufficiently small, one can approximate the difference $z(x+\Delta x, y+ \Delta y) - z(x+\Delta x, y)$ by $z(x, y+ \Delta y) - z(x, y)$.

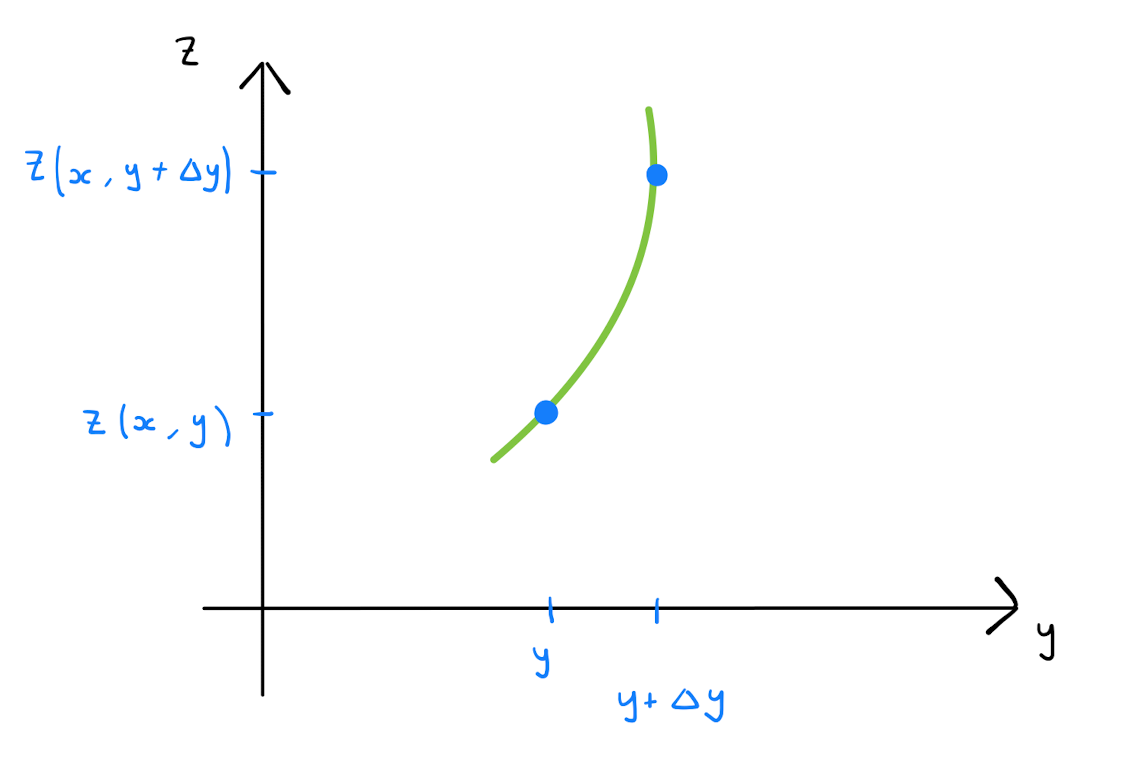
By treating $x$ as a fixed value and $y$ as the sole variable, one concludes by the theory of small changes for univariate functions that $$z(x+\Delta x, y+ \Delta y) - z(x+\Delta x, y) \approx \Delta y \frac{\partial z}{\partial y}$$

Therefore one can approximate $\Delta z$ by $$\Delta z \approx \frac{\partial z}{\partial x} \Delta x + \frac{\partial z}{\partial y} \Delta y.$$

The volume $V$ of a cylinder is given in terms of the radius $r$ and height $h$ by the formula $V= \pi r^2 h$. Find $\Delta V$ in terms of small changes $\Delta r$ and $\Delta h$, both by direct compution and by using the theory of small changes.

‘Direct Computation’ $$\begin{align*} V + \Delta V &= \pi (r + \Delta r)^2 (h + \Delta h) \\ &= \pi (r^2 + 2 r \Delta r + \Delta r^2)(h + \Delta h) \\ &= \pi r^2 h + 2 \pi rh \Delta r + \pi h \Delta r^2 + \pi r^2 \Delta h + 2 \pi r \Delta r \Delta h + \pi \Delta r^2 \Delta h \\ &= \left( \pi r^2 h \right) + \left( 2 \pi rh \Delta r + \pi r^2 \Delta h \right) + \text{'higher order terms in $\Delta r$ and $\Delta h$'} \\ &\approx V + 2 \pi rh \Delta r + \pi r^2 \Delta h, \\ \Delta V &\approx 2 \pi rh \Delta r + \pi r^2 \Delta h. \end{align*}$$

‘Theory of Small Changes’
Since $V = \pi r^2 h$, calculate:

$$\begin{align*} \frac{\partial V}{\partial r} &= 2 \pi r h, \\[5pt] \frac{\partial V}{\partial h} &= \pi r^2. \end{align*}$$

It follows

$$\begin{align*} \Delta V &\approx \frac{\partial V}{\partial r} \Delta r + \frac{\partial V}{\partial h} \Delta h \\ &= 2 \pi r h \Delta r + \pi r^2 \Delta h. \end{align*}$$

Note the comparative ease of using the theory of small changes compared to the direct computation, even with a relatively straightforward function.

Considering again the cylinder of Example 5.1.1, if the radius $r$ and height $h$ increase by $3 \%$ and $1 \%$ respectively what is the approximate percentage increase in the volume $V$?

The percentage increase of $r$ and $h$ tell us that

$$\frac{\Delta r}{r} = 0.03, \qquad \text{and} \qquad \frac{\Delta h}{h} = 0.01.$$ Using the Example 5.1.1, the proportion by which $V$ increases is given by $$\begin{align*} \frac{\Delta V}{V} &= \frac{2 \pi r h \Delta r + \pi r^2 \Delta h}{\pi r^2 h} \\ &= 2 \frac{\Delta r}{r} + \frac{\Delta h}{h} \\ &= 2 \cdot 0.03 + 0.01 \\ &= 0.07 \end{align*}$$

Therefore $V$ will increase by $7 \%$.

5.2 Differentials

Looking again at the univariate function $y=y(x)$ consider the limit in the theory of Section 5.1 as $\Delta x \rightarrow 0$, that is as the change made in $x$ becomes infintesimally small. The approximation $\Delta y \approx \frac{d y}{d x} \Delta x$ becomes an equality and is written in the form $$dy = \frac{dy}{dx} dx.$$

The infinitesimal changes $dx$ and $dy$ are called differentials.

Similarly looking at a function of two variables $z=z(x,y)$, and considering small changes $\Delta x, \Delta y$ in the variables $x$ and $y$ respectively. The corresponding change in $z$ is given approximately by $\Delta z \approx \frac{\partial z}{\partial x} \Delta x + \frac{\partial z}{\partial y} \Delta y$. Letting both $\Delta x, \Delta y \rightarrow 0$, that is letting both changes become infinitesimally small, the approximation becomes an equality of differentials: $$dz = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy.$$ The differentials $dx$ and $dy$ are treated as independent variables.

Let $x=x(r,\theta) = r \cos \theta$ and $y= y(r,\theta) = r \sin \theta$. Use differentials to find $\frac{\partial r}{\partial x}$ and $\frac{\partial r}{\partial y}$.

Note that one cannot assume $\frac{\partial r}{\partial x} \neq \frac{1}{\left( \frac{\partial x}{\partial r} \right)}$ as is the case for multivariate functions in general. This is a key difference between the ordinary derivative of a univariate function and partial derivatives.

Instead apply the theory of differentials to obtain $$\begin{equation*}\tag{$\star$} dx = \frac{\partial x}{\partial r} dr + \frac{\partial x}{\partial \theta} d \theta = \cos \theta dr + (-r \sin \theta) d\theta, \end{equation*}$$ and $$\begin{equation}\tag{$\star \star$} dy = \frac{\partial y}{\partial r} dr + \frac{\partial y}{\partial \theta} d \theta = \sin \theta dr + r \cos \theta d\theta. \end{equation}$$ Calculating $\cos \theta \cdot (\star) + \sin \theta \cdot (\star \star)$, obtain $$\begin{align*} \cos \theta \cdot dx + \sin \theta \cdot dy &= \cos^{2} \theta \cdot dr - r \sin \theta \cos \theta \cdot d \theta + \sin^{2} \theta \cdot dr + r \sin \theta \cos \theta \cdot d\theta \\ &= \left( \cos^{2} \theta + \sin^{2} \theta \right) dr \\ &= dr. \end{align*}$$ Alternatively the variable $r$ could be thought of in terms of $x$ and $y$. Therefore by the theory of differentials $dr = \frac{\partial r}{\partial x} dx + \frac{\partial r}{\partial y} dy$. By comparing coefficients of $dx$ and $dy$ between the two obtained expressions for $dr$, one obtains $$\frac{\partial r}{\partial x} = \cos \theta, \qquad \text{and} \qquad \frac{\partial r}{\partial y} = \sin \theta.$$

Calculate $\frac{\partial \theta}{\partial x}$ and $\frac{\partial \theta}{\partial y}$ from Example 5.2.2 using the theory of differentials.