Chapter 4 Partial Derivatives
4.1 Recap of Ordinary Derivatives
Consider \(y=y(x) = f(x)\), a univariate function. Specifically, \(y\) is the dependent variable and \(x\) is the only independent variable. We are all familiar with studying the rate of change of \(y\) as \(x\) changes. The formal mathematical definition was introduced in the Autumn semester.
The derivative of \(y\) with respect to \(x\) is given by
The motivation of the definition can be seen graphically. The numerator of the fraction represents a change in \(y\)-coordinate between the points \(\big(x,f(x) \big)\) and \(\big(x+h,f(x+h) \big)\), while the denominator represents a change in \(x\)-coordinate. This presents the gradient of the line between the two points. As \(h \rightarrow 0\), this line approaches the tangent line.
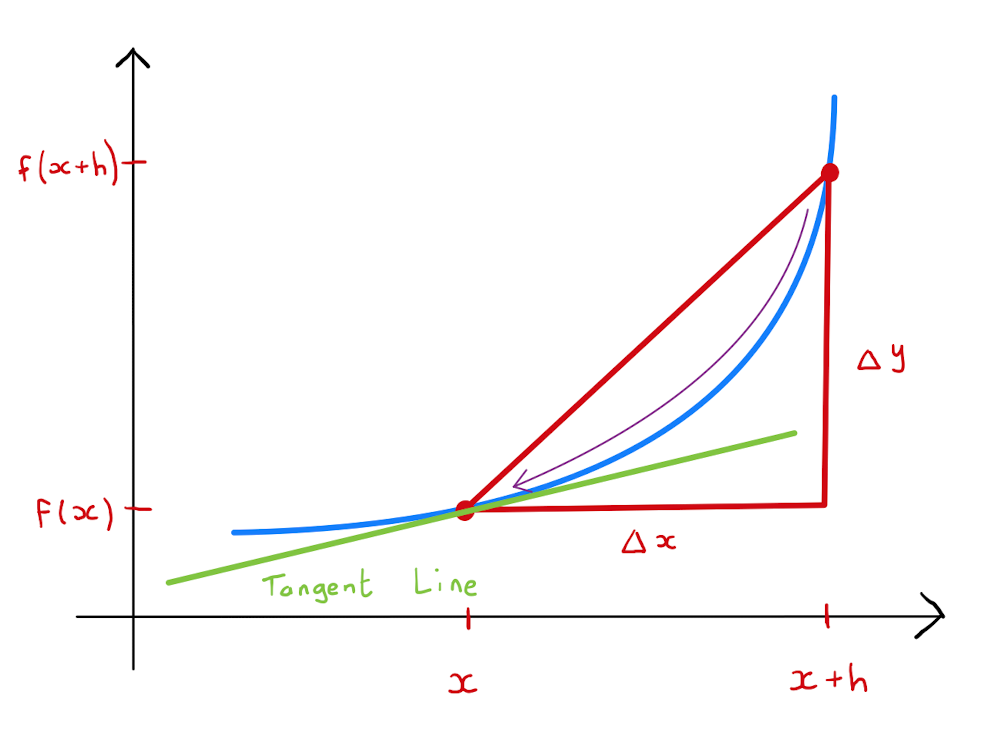
The derivative of \(y=y(x) = f(x)\) is also often denoted by \(y'(x), \frac{d}{dx} (y)\) or \(\frac{d y}{d x}\). Note the use of the roman numerical ‘d’ in these notations.
The derivatives of a number of standard functions are well known.
| \(\mathbf{f(x)}\) | \(\mathbf{f'(x)}\) |
|---|---|
| \(ax^n\) | \(an x^{n-1}\) |
| \(\sin(x)\) | \(\cos(x)\) |
| \(\cos(x)\) | \(-\sin(x)\) |
| \(e^x\) | \(e^x\) |
| \(\ln (x)\) | \(\frac{1}{x}\) |
Prove formally using Definition 4.1.1 that each of these standard functions has the derivative as stated.
4.2 Introduction to Partial Derivatives
Let \(z = z(x,y) = f(x,y)\) be a function of two variables.
The partial derivative of \(z\) with respect to \(x\), denoted by \(\frac{\partial z}{\partial x}\) or \(\frac{\partial}{\partial x}(z)\), is found by differentiating the expression \(f(x,y)\) treating \(y\) as an unknown constant and \(x\) as the only variable.
Similarly the partial derivative of \(z\) with respect to \(y\) denoted by \(\frac{\partial z}{\partial y}\) or \(\frac{\partial}{\partial y}(z)\), is found by differentiating the expression \(f(x,y)\) treating \(x\) as an unknown constant and \(y\) as the only variable.
Note the use of ‘\(\partial\)’ called a partial or a del, rather than ‘d’ in the partial derivative notation. It is important to use these notations correctly.
Consider \(z = a x y^n\). Calculate \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\).
By differentiating \(z = a x y^n\) treating \(x\) as a variable and \(y\) as a constant, obtain
\[\frac{\partial z}{\partial x} = ay^n.\]
Similarly differentiating \(z = a x y^n\) treating \(y\) as a variable and \(x\) as a constant, obtain
\[\frac{\partial z}{\partial y} = a n x y^{n-1}.\]
Consider \(z = x^4 + 3y^2 + y \sin (x)\). Calculate \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\).
One finds that
The definition of a partial derivative easily generalises to a function of \(n\) variables where \(n>2\).
4.3 Higher Order Partial Derivatives
Note in Example 4.2.2 and Example 4.2.3 that both \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\) are functions of \(x\) and \(y\). This is true in general for any function \(z(x,y)\). Since \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\) are functions of \(x\) and \(y\), they themselves can be differentiated to with respect to \(x\) and \(y\).
The second order partial derivatives of \(z=z(x,y)\) are given by
A common alternative notation is to use a subscript on \(z\) to indicate a partial derivative. Specifically \[\begin{align*} z_x = \frac{\partial z}{\partial x}, &\qquad z_y = \frac{\partial z}{\partial y}, \\[5pt] z_{xx} = \frac{\partial^{2} z}{\partial x^2}, &\qquad z_{xy} = \frac{\partial^{2} z}{\partial y \partial x}. \end{align*}\]
Consider \(z = x^4 + 3y^2 + y \sin (x)\) from Example 4.2.3. We calculated that \[\begin{align*} \frac{\partial z}{\partial x} &= 4 x^3 + y \cos(x), \\ \frac{\partial z}{\partial y} &= 6y + \sin(x). \end{align*}\] It follows that
In Example 4.3.2, the two second derivatives \(\frac{\partial^{2} z}{\partial y \partial x}\) and \(\frac{\partial^2 z}{\partial x \partial y}\) are equal. This is a property that holds for all sufficiently nice functions. The exact statement is given by Clairaut’s Theorem.
Clairaut’s Theorem. Consider \(z=f(x,y)\) a two variable real-valued function. If \(\frac{\partial^2 z}{\partial x \partial y}\) and \(\frac{\partial^2 z}{\partial y \partial x}\) are both continuous on the domain, then \[\frac{\partial^2 z}{\partial x \partial y} = \frac{\partial^2 z}{\partial y \partial x}.\]
Typically in this module we will consider nice functions that satisfy the conditions of Clairaut’s theorem. Hence normally \(z(x,y)\) has three independent second order partial derivatives.
Consider the function
\[z = \begin{cases} \frac{xy(x^2 - y^2)}{x^2 + y^2}, & \text{if } (x,y) \neq (0,0), \\ 0, & \text{if } (x,y) = (0,0). \end{cases}\] Calculate \(\frac{\partial^2 z}{\partial x \partial y}\) and \(\frac{\partial^2 z}{\partial y \partial x}\). Why does this not contradict Clairaut’s Theorem?
4.4 Geometrical Interpretation of Partial Derivatives
In the univariate case, the geometrical interpretation of the derivative is well understand. Specifically if the function \(y=f(x)\) defines a curve, then the derivative \(\frac{dy}{dx}\) describes the gradient of the tangent line to curve. Partial derivatives have a similar geometric interpretation in the multivariate case.
Let \(z = f(x,y)\). We saw in Section 1.3 that the function will describe a surface \(S\). Let \(\big(a,b, f(a,b) \big)\) be a point on this surface.
Calculating \(\frac{\partial z}{\partial x}\) involves treating \(y\) as a constant. Suppose that this constant value for \(y\) is \(b\). Well in that case, \(f(x,b)\) is a function of one variable and so one can calculate the derivative of this one variable function. It is routine to verify using the formal definition of a derivative that \[\frac{\partial z}{\partial x}(x,b) = \frac{d}{dx} \big( f(x,b) \big)\].
Geometrically the univariate function \(f(x,b)\) will describe a curve \(C\). This curve will be a cross-section of the surface \(S\), since we are allowing the variable \(x\) to vary while keeping the \(y\) fixed. From the theory of derivatives of univariate functions, we know that \(\frac{\partial z}{\partial x}(x,b) = \frac{d}{dx} \big( f(x,b) \big)\) is the tangent vector to the curve \(C\). This vector will also lie tangent to the surface \(S\) and will point in the direction of varying \(x\).
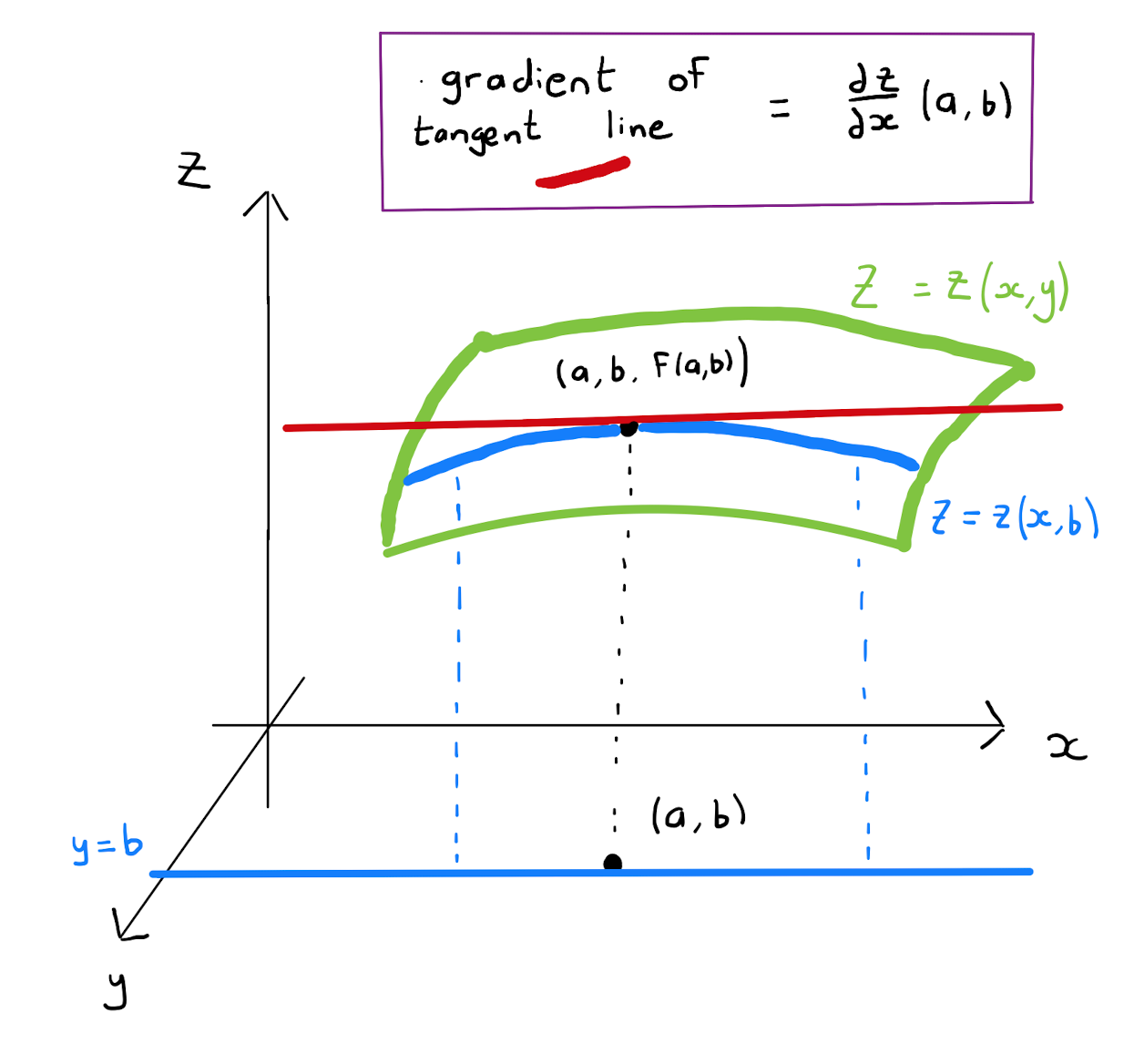
This proves the following result.
Consider a surface described by a multivariate function \(z=z(x,y)\). The partial derivative \(\frac{\partial z}{\partial x}\) is a tangent vector describing the slope of the surface in the \(x\)-direction.
A similar result holds for the partial derivative with respect to \(y\).
Consider a surface described by a multivariate function \(z=z(x,y)\). The partial derivative \(\frac{\partial z}{\partial y}\) is a tangent vector describing the slope of the surface in the \(y\)-direction.
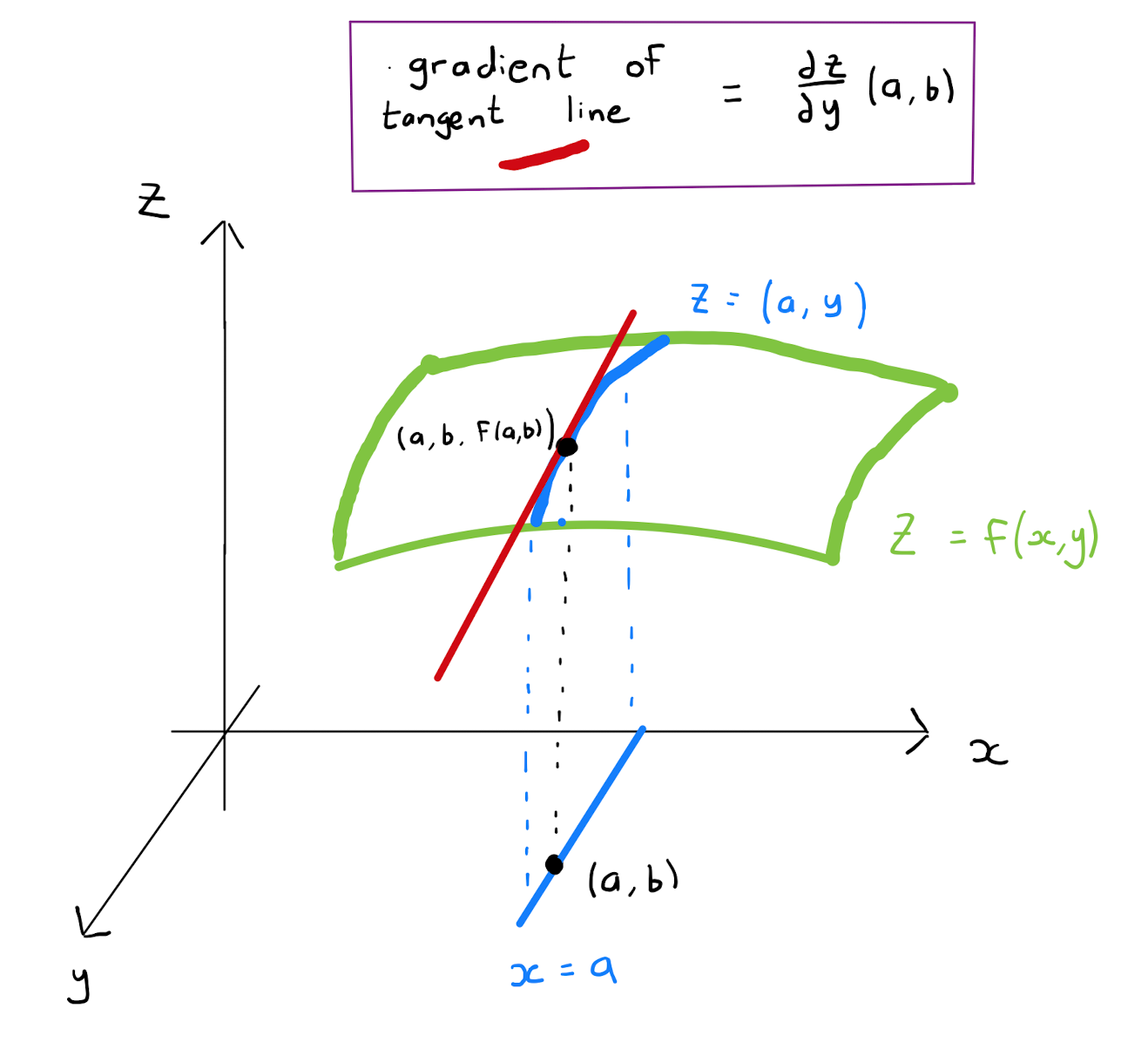
4.5 Implicit Differentiation
All of the multivariate functions we have seen so far have been explicit:
A function of two variables \(z(x,y)\) is explict if it can be written algebraically in the form \[z = f(x,y),\] that is, the dependent variable is equal to some expression in terms of the independent variables only.
A function of two variables \(z(x,y)\) that is not explicit is called implicit. Implicit functions \(z(x,y)\) will be described as satisfying some condition \(f(x,y,z)=0\), where an expression of the dependent and independent variables is equal to \(0\).
An implicit function \(f(x,y,z)=0\) still represents a surface: the set of points in \(\mathbb{R}^{3}\) that satisfy the equation.
A function that is described implicitly is \(x^2 + y^2 + z^2 - 1 =0\), the equation of a sphere. The \(z^2\) is stopping us from writing the equation in the form \(z=f(x,y)\) for some function \(f\).
One might be tempted to argue that the sphere in Example 4.5.3 could be written in the form \(z = \pm \sqrt{1-x^2-y^2}\). However ‘\(\pm\)’ is not a mathematical expression. It is simply a notation to indicate that there are two distinct (explicit) cases to be considered: \(z= \sqrt{1-x^2-y^2}\) and \(z = -\sqrt{1-x^2-y^2}\). Imagine trying to concoct a similar notation to express the explicit cases that arise from \(x^9 + y^9 + z^9 - 1 =0\) in this fashion.
A key geometric feature of a surface described by an implicit function is that for a fixed point \((x,y)\) there may be multiple values of \(z\) for which \((x,y,z)\) belongs to the surface: consider the sphere in Example 4.5.3. It is clear that this not possible in the explicit case.
Nonetheless for an implicit function \(z(x,y)\), just as for an explicit function, as the independent variables \(x\) and \(y\) change, the value of the dependent variable \(z\) will change. It is natural to query the rate of this change, that is, one still wants to calculate the partial derivatives \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\).
The technique of implicit differentiation allows us to differentiate the equation of an implicit function. Simply differentiate both sides of the equality as expressions in \(x\) and \(y\). Whenever a \(z\) appears, apply the chain rule remembering that \(z\) is a function of \(x\) and \(y\).
Remember that when partial differentiating with respect to \(x\) one treats \(x\) as a variable, \(y\) as a constant and vice versa when partial differentiating with respect to \(y\).
Consider the function \(z(x,y)\) given implicitly by \(xy + z^2 + xz =0\). Calculate
\(\frac{\partial z}{\partial x}\)
\(\frac{\partial z}{\partial y}\)
“(a.)” Partial differentiating both sides of \(xy + z^2 + xz =0\) with respect to \(x\) obtain
\[\begin{align*}
\frac{\partial}{\partial x} \big( xy + z^2 + xz \big) &= \frac{\partial}{\partial x} \big( 0 \big), \\
\frac{\partial}{\partial x} \big( xy \big) + \frac{\partial}{\partial x} \big(z^2\big) + \frac{\partial}{\partial x} \big(xz \big) &= 0.
\end{align*}\]
Note that
\(\frac{\partial}{\partial x} \big( xy \big) = y\);
By the chain rule \(\frac{\partial}{\partial x} \big(z^2\big) = 2 \frac{\partial z}{\partial x} z\);
By the product rule \(\frac{\partial}{\partial x} \big(xz \big) = z + x\frac{\partial z}{\partial x}\).
Therefore by substitution
“(b.)” Partial differentiating both sides of \(xy + z^2 + xz =0\) with respect to \(y\) obtain \[\begin{align*} \frac{\partial}{\partial y} \big( xy + z^2 + xz \big) &= \frac{\partial}{\partial y} \big( 0 \big), \\ \frac{\partial}{\partial y} \big( xy \big) + \frac{\partial}{\partial y} \big(z^2\big) + \frac{\partial}{\partial y} \big(xz \big) &= 0, \\ x + 2 \frac{\partial z}{\partial y} z + x \frac{\partial z}{\partial y} &= 0, \\ \frac{\partial z}{\partial y} (2z+x) &= -x, \\ \frac{\partial z}{\partial y} &= - \frac{x}{2z+x}. \end{align*}\]
It may appear unusual in Example 4.5.5 that the expression for \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\) both involve \(z\). However remembering that \(z\) is a function of \(x\) and \(y\) makes this more natural.