Chapter 8 Analysis of binary and ordinal outcomes
Binary outcomes are ubiquitous in medical research and the comparison of binary outcomes in RCTs is very common. This chapter discusses various statistical quantities that can be calculated for comparing binary outcomes. We discuss statistical tests, suitable effect measures and methods to adjust for possible baseline variables. Ordinal outcomes are also discussed at the end of this chapter.
8.1 Comparison of two proportions
Throughout this section, we will work with the following example.
Example 8.1 The APSAC study is an RCT comparing a new thrombolytikum (APSAC) with the standard treatment (Heparin) in patients with acute cardiac infarction (Meinertz et al, 1988). The outcome is mortality within 28 days of hospital stay. Table 8.1 summarizes the results of this study, including 95% Wilson CIs for the proportion of patients who died in the respective treatment groups.
| Therapy | Dead | Alive | Total | Percent Dead | Standard Error | 95% Wilson-CI |
|---|---|---|---|---|---|---|
| APSAC | 9 | 153 | 162 | 5.6% | 1.8% | 3.0 to 10.2 |
| Heparin | 19 | 132 | 151 | 12.6% | 2.7% | 8.2 to 18.8 |
| Total | 28 | 285 | 313 |
A visual comparison for the two separate CIs in Figure 8.1 shows that they overlap. However, overlapping CIs are not necessarily an indication for a non-significant treatment effect. Instead, we should rather look at CIs for combined effect measures such as the ones presented in Definition 8.1.
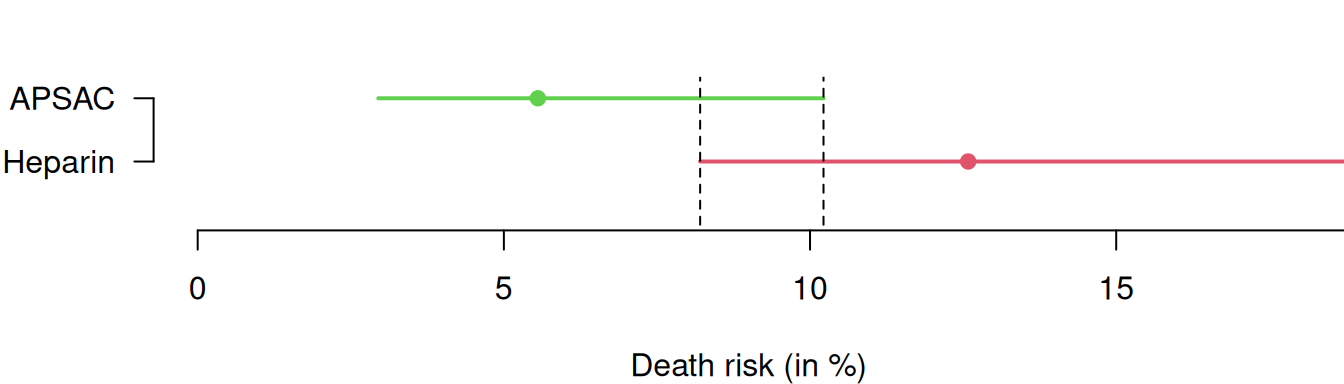
Figure 8.1: 95% Wilson confidence intervals for the death risks in the APSAC study.
8.1.1 Statistical tests
Commonly used tests to compare two proportions are the \(\chi^2\)-test
and Fisher’s “exact” test for small samples.
The null hypothesis in these tests is that there is no difference
between groups.
Both methods give a \(P\)-value, but no effect measure. There is a second
version of the \(\chi^2\)-test which uses a continuity correction. Furthermore,
there are at least three different versions to calculate the two-sided \(P\)-value
for Fisher’s “exact” test (see the R package exact2x2
for details).
Example 8.1 (continued) The \(\chi^2\)-test and Fisher’s exact test are applied to the APSAC study in the
following R code:
## dead alive
## APSAC 9 153
## Heparin 19 132## dead alive
## APSAC 14.49201 147.508
## Heparin 13.50799 137.492##
## Pearson's Chi-squared test
##
## data: APSAC.table
## X-squared = 4.7381, df = 1, p-value = 0.0295##
## Fisher's Exact Test for Count Data
##
## data: APSAC.table
## p-value = 0.04588
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
## 0.1576402 0.9892510
## sample estimates:
## odds ratio
## 0.409812Note that the function fisher.test() also provides an estimate
(conditional MLE) of the odds ratio (with 95% CI).
The output from the \(\chi^2\)-test can also be used to compute
an estimate of the relative risk based on the observed to expected death ratios:
mytest <- chisq.test(APSAC.table)
o <- mytest$observed[,"dead"]
e <- mytest$expected[,"dead"]
print(ratio <- (o/e))## APSAC Heparin
## 0.6210317 1.4065752## APSAC
## 0.44152058.1.2 Effect measures and confidence intervals
Let \(\pi_0\) and \(\pi_1\) denote the true risks of death in the control and intervention group, respectively, with \(\pi_0 \geq \pi_1\).
Definition 8.1 The following quantities are used to compare \(\pi_0\) and \(\pi_1\):
The absolute risk reduction \[\mbox{ARR}= \pi_0-\pi_1.\]
The number needed to treat \[\mbox{NNT}= 1 / \mbox{ARR}.\]
The relative risk \[\mbox{RR}= {\pi_1}/{\pi_0}.\]
The relative risk reduction \[\mbox{RRR}= \frac{\mbox{ARR}}{\pi_0} = 1 - \mbox{RR}.\]
The odds ratio \[\mbox{OR}= \frac{\pi_1/(1-\pi_1)}{\pi_0/(1-\pi_0)}.\]
No difference between groups (i.e. \(\pi_0 = \pi_1\)) corresponds to \(\mbox{ARR}=\mbox{RRR}=0\) and \(\mbox{RR}=\mbox{OR}=1\). We now discuss each of these effect measures together with their CIs using Example 8.1.
Absolute Risk Reduction
The ARR is also called risk difference (\(\mbox{RD}\)) or probability difference. The estimated ARR
\[\widehat{\mbox{ARR}} \ = \ 12.6\%-5.6\%=7\%\]
with standard error
\[ \mbox{se}(\widehat{\mbox{ARR}}) = \sqrt{\frac{\hat \pi_0 (1-\hat \pi_0)}{n_0}+\frac{\hat \pi_1 (1-\hat \pi_1)}{n_1}}= 3.2\%. \]
\(\widehat{\mbox{ARR}}\) and \(\mbox{se}(\widehat{\mbox{ARR}})\) can be used to
calculate a Wald CI for the ARR.
An improved Wilson CI for the ARR can be calculated using the
“square-and-add” approach (Newcombe, 2013; Newcombe, 1998a),
see Appendix A.2.3 and the function
biostatUZH::confIntSquareAdd() for details.
The following R code provides both Wald and Wilson CIs for the ARR in the APSAC study. They are visually compared in Figure 8.2. There are no large differences between the two types of confidence intervals, only the upper limit of the Wilson is slightly larger than the corresponding Wald upper limit.
## $rd
## [,1]
## [1,] 0.07027226
##
## $CIs
## type lower upper
## 1 Wald 0.006691788 0.1338527
## 2 Wilson 0.006303897 0.1378381Using articifial data, the lower plot in Figure 8.2 highlights the distinct advantage of the Wilson confidence interval: its ability to prevent overshoot. Indeed, the upper limit of the Wald confidence interval for the risk difference is larger than 1 whereas this is not the case for the Wilson interval.
## $rd
## [,1]
## [1,] 0.8333333
##
## $CIs
## type lower upper
## 1 Wald 0.6121830 1.054484
## 2 Wilson 0.4507227 0.930162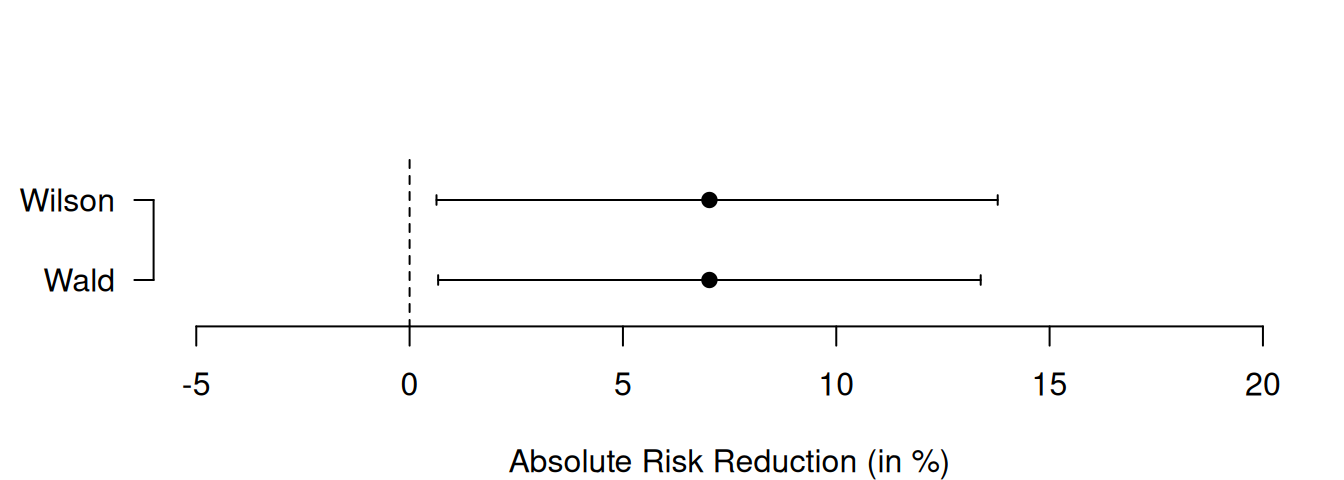
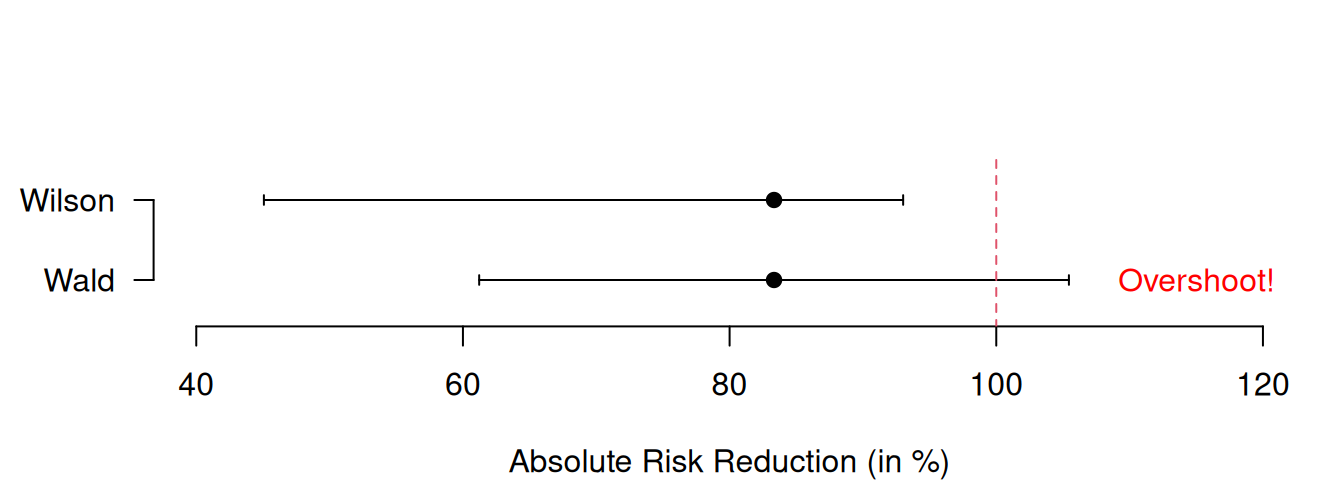
Figure 8.2: Wald and Wilson CIs for the ARR in the APSAC study (upper plot) and in an example with artifical data illustrating overshoot (lower plot).
Number Needed to Treat
Suppose we have \(n\) patients in each treatment group. The expected number of deaths in the control and intervention group are: \[\begin{eqnarray*} N_0 & = & n \, \pi_0, \\ N_1 & = & n \, \pi_1. \end{eqnarray*}\] The expected difference is therefore \(N_0-N_1 = n \, (\pi_0-\pi_1)\). Suppose we want the difference \(N_0 - N_1\) to be one patient. The required sample size \(n\) to achieve this is \[ n = 1/(\pi_0-\pi_1) = 1/\mbox{ARR}. \] This is the number needed to treat, the required number of patients to be treated with the intervention rather than control to avoid one death. Depending on the direction of the effect, the NNT is also called number needed to benefit or number needed to harm.
The interpretation of the estimated \(\mbox{NNT}\)
\[\quad \widehat{\mbox{NNT}} \ = \ 1/\widehat{\mbox{ARR}} \ = \ 1 / 0.07 \ = \ 14.2\]
in the APSAC study is the following: To avoid one death, we need to treat \(\widehat{\mbox{NNT}} = 14.2\) patients with APSAC rather than with Heparin. A confidence interval for \(\mbox{NNT}\) can be obtained by inverting the limits \(\mbox{L}_{\mbox{ARR}}\) and \(\mbox{U}_{\mbox{ARR}}\) of the CI for \(\mbox{ARR}\):
## type lower upper
## 2 Wilson 0.006303897 0.1378381## lower upper
## 2 7.3 158.6The CI for \(\mbox{NNT}\) in the APSAC study is: \(1 / 0.138\) to \(1 / 0.006\) = \(7.3\) to \(158.6\).
Note that the CI for \(\mbox{NNT}\) is not well-defined if the CI for \(\mbox{ARR}\) contains 0. In that case, the confidence interval is actually a confidence region, comprising two different intervals depending on the direction of the treatment effect (Altman, 1998). This problem can be circumvented by plotting the number needed to treat on the absolute risk reduction scale, as illustrated in the following example.
Example 8.2 Figure 8.3 shows a forest plot reproduced from Altman (1998) where an overall number needed to benefit is calculated from a meta-analysis of data from randomized trials comparing bypass surgery with coronary angioplasty in relation to angina in one year (Pocock et al, 1995). For three studies (CABRI, RITA, EAST), the 95% confidence interval for NNT is a regular interval and includes only values that indicate a benefit of therapy. However, for two other entries (GABI and Other) the confidence region for NNT splits into two intervals. For example, for GABI the two intervals are 7.5 to infinity for benefit and 14.5 to infinity for harm. This indicates that this trial is inconclusive regarding the direction of the treatment effect with large uncertainty regarding the actual value of NNT.
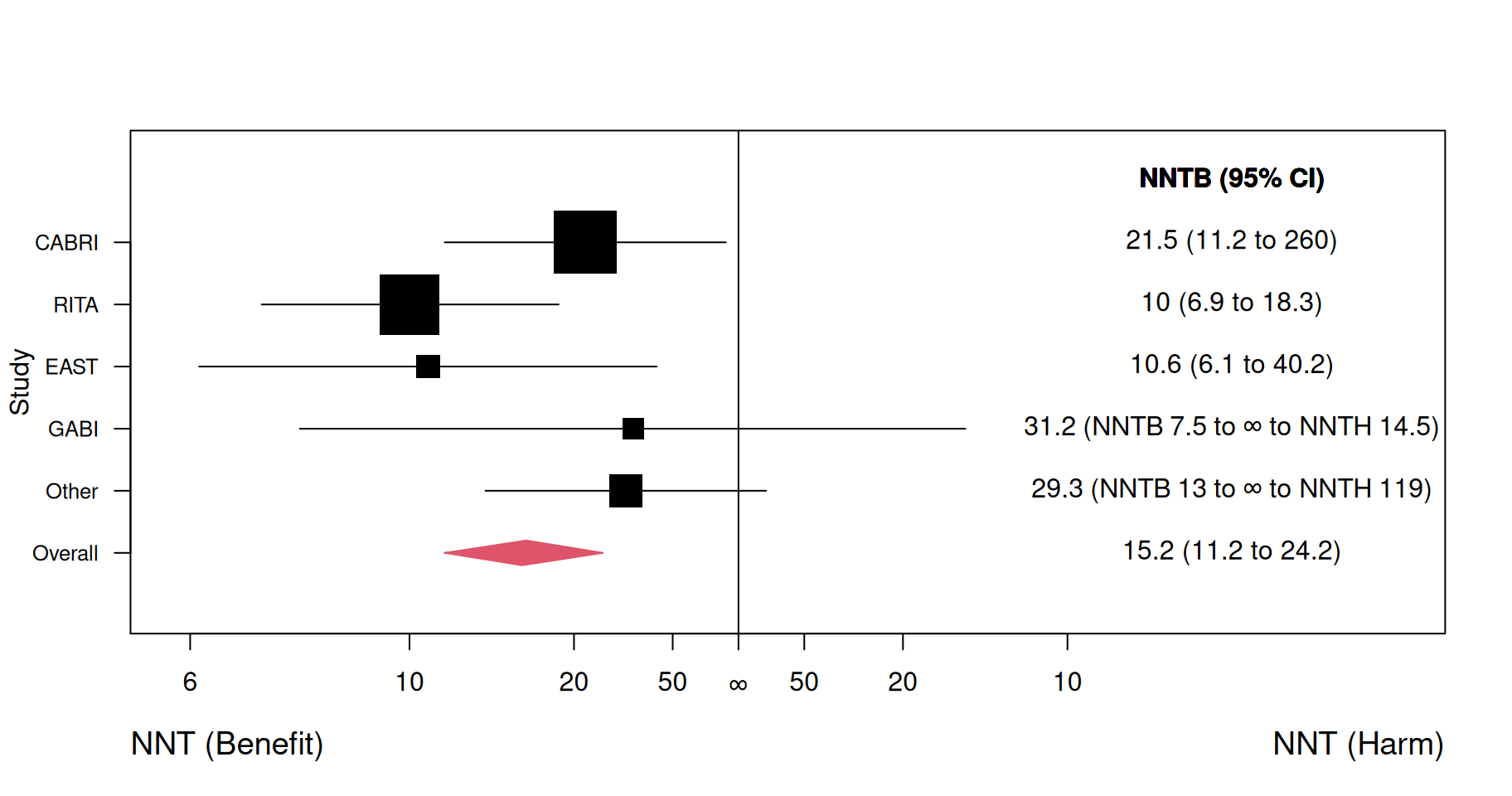
Figure 8.3: Forest plot for NNT (benefit = NNTB, harm = NNTH) in a meta-analysis. Figure reproduced from Figure 3 in Altman (1998).
Relative Risk
The relative risk (RR) is also called risk ratio. The estimated death risks in both treatment groups from Example 8.1 are
- \(x_1/n_1=9/162=5.6\%\) for APSAC and
- \(x_0/n_0=19/151=12.6\%\) for Heparin.
The estimated RR is therefore
\[\widehat{\mbox{RR}} = \frac{5.6\%}{12.6\%} = 0.44.\]
The calculation of a CI for the RR is based on the logRR as explained in Table 8.2. With the standard error of the log RR
\[ \mbox{se}(\color{red}{\log}(\widehat{\mbox{RR}})) = \sqrt{\frac{1}{x_1}-\frac{1}{n_1}+\frac{1}{x_0}-\frac{1}{n_0}} \]
and the corresponding \[ \mbox{EF}_{.95} = \exp\left\{1.96 \cdot \mbox{se}(\color{red}{\log}(\widehat{\mbox{RR}}))\right\}, \] we can directly calculate the limits of the CI for the RR as
\[\begin{equation} \tag{8.1} \widehat{\mbox{RR}}/\mbox{EF}_{.95} \text{ and } \widehat{\mbox{RR}} \cdot \mbox{EF}_{.95}. \end{equation}\]
This calculation is implemented in the R function
biostatUZH::confIntRiskRatio().
## lower Risk Ratio upper
## 0.2061781 0.4415205 0.9454948| Quantity | Estimate | Standard Error | 95%-confidence interval |
|---|---|---|---|
| RR | 0.44 |
|
0.21 to 0.95 |
| ↓ log ↓ | ↑ exp ↑ | ||
| log RR | -0.82 | 0.39 | -1.58 to -0.06 |
The square-and-add method can also be applied to ratio measures such as the risk ratio (Newcombe, 2013, sec. 7.3.4), but this is rarely used in practice. One reason might be that the simple approach (8.1) based on error factors is – by construction – not prone to overshoot below zero.
Relative Risk Reduction
Either \(\mbox{ARR}\) or \(\mbox{RR}\) can be used to estimate \(\mbox{RRR}\): \[\begin{eqnarray*} \widehat{\mbox{RRR}} & = & \frac{\widehat{\mbox{ARR}}}{\widehat{\pi}_0} \ = \ \frac{0.07}{0.126} \ = \ 56\% \mbox{ or} \\ \widehat{\mbox{RRR}} & = & 1-\widehat{\mbox{RR}} \ = \ 1 - 0.44 \ = \ 56\%. \end{eqnarray*}\] A CI for \(\mbox{RRR}\) can be obtained based on the limits \(\mbox{L}_{\mbox{RR}}\) and \(\mbox{U}_{\mbox{RR}}\) of the CI for \(\mbox{RR}\):
\[\begin{eqnarray*} (1 - \mbox{U}_{\mbox{RR}}) \mbox{ to } (1 - \mbox{L}_{\mbox{RR}}) & = & (1 - 0.95) \mbox{ to } (1 - 0.21) \\ & = & 0.05 \mbox{ to } 0.79 \end{eqnarray*}\]
So, the risk of death with APSAC has been reduced by 56% (95% CI: 5% to 79%) compared to Heparin.
Odds Ratio
| Yes | No | Total | |
|---|---|---|---|
| APSAC | \(a=9\) | \(b=153\) | \(162\) |
| Heparin | \(c=19\) | \(d=132\) | \(151\) |
| \(n = 313\) |
From Table 8.3, we can read that the estimated odds of death for APSAC are \(a/b = 9/153\) (\(c/d=19/132\) for Heparin). The estimated OR is therefore \[ \widehat{\mbox{OR}} = \frac{a / b}{c / d} = \frac{9 / 153}{19 / 132} = \frac{9 \cdot 132}{153 \cdot 19} \ = 0.41. \] This means that the odds of death are 59% lower under APSAC than under Heparin treatment. The rearrangement \[\begin{equation} \tag{8.2} \widehat{\mbox{OR}}=(a\cdot d) / (b \cdot c) \end{equation}\] motivates the alternative name cross-product ratio.
| Dead | Alive | Total | Percent Alive | Standard Error | 95% CI | |
|---|---|---|---|---|---|---|
| APSAC | 9 | 153 | 162 | 94.4% | 1.8% | 98.0 to 90.9% |
| Heparin | 19 | 132 | 151 | 87.4% | 2.7% | 92.7 to 82.1% |
An advantage of the ORs is that they can be inverted for complementary events. If we consider the survival probability rather than the death risk as in Table 8.4, we can see that:
- The odds ratio for death risk is \(\mbox{OR}=0.41\).
- The odds ratio for survival then is
\[ \frac{(1-\pi_1)/\pi_1}{(1-\pi_0)/\pi_0} = \frac{\pi_0/(1-\pi_0)}{\pi_1/(1-\pi_1)} = 1/\mbox{OR}= 1/0.41 = 2.45. \]
Such a relationship does not hold for relative risks: \[ 1/\mbox{RR}= 1/0.44 = 2.25, \mbox{ but } 94.4\%/87.4\% = 1.08. \]
A disadvantage of the ORs is their noncollapsibility (Senn, 2021). Consider a hypothetical example with two therapies and two strata. Table 8.5 presents a contingency table stratified by strata, while Table 8.6 present the collapsed contingency table.
| Yes | No | Total | Yes | No | Total | |
|---|---|---|---|---|---|---|
| Therapy A | 80 | 20 | 100 | 60 | 40 | 100 |
| Therapy B | 60 | 40 | 100 | 36 | 64 | 100 |
| Yes | No | Total | |
|---|---|---|---|
| Therapy A | 140 | 60 | 200 |
| Therapy B | 96 | 104 | 200 |
The OR for Stratum 1 is \(\mbox{OR} = \frac{80 \cdot 40}{20 \cdot 60} = 2.67\)
The OR for Stratum 2 is \(\mbox{OR} = \frac{60 \cdot 64}{40 \cdot 36} = 2.67\)
The OR from the collapsed analysis is \(\mbox{OR} = \frac{140 \cdot 104}{60 \cdot 96} = 2.53\)
\(\rightarrow\) The ORs are the same in both strata, but the OR collapsed over strata is different.
As for \(\mbox{RR}\) (see Table 8.2), we calculate the standard error of the OR on the log scale: \[\begin{equation} \tag{8.3} \mbox{se}(\color{red}{\log}(\widehat{\mbox{OR}})) = \sqrt{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}}. \end{equation}\]
A multiplicative Wald CI can be directly calculated using the 95% error factor
\[ \mbox{EF}_{.95} = \exp\left\{1.96 \cdot \mbox{se}(\color{red}{\log}(\widehat{\mbox{OR}}))\right\}. \] Note that CIs for odds ratios may differ even if group sample sizes remain the same:
## lower Odds Ratio upper
## 0.4565826 1.0000000 2.1901841## lower Odds Ratio upper
## 0.06081319 1.00000000 16.44380070What matters is the number of events.
A problem of the estimate (8.2) is that it can become infinite
if either \(b=0\) or \(c=0\). Likewise, the standard error (8.3)
of the log odds ratio will be infinte if at least one of the entries
\(a\), \(b\), \(c\) or \(d\) is zero. A modification suggested in the
literature is to add \(1/2\) to all entries \(a\), \(b\), \(c\) and \(d\). This
prevents problems with small number of events and also reduces the
potential bias of the original estimate, see for example
Spiegelhalter et al (2004), Section 2.4.1. Another estimate of the odds ratio
is the conditional maximum likelihood estimate. This is related to
Fisher’s exact test as it is based on numerically maximizing the
hypergeometric likelihood, which depends only on the odds ratio and is
obtained by conditioning on the margins sums. The conditional MLE
estimate is often reported together with the \(P\)-value from Fisher’s
exact test, as in the R function fisher.test(). However, it has the
same problem as the standard (unconditional) MLE (8.2) that it
becomes infinite if either \(b\) or \(c\) is zero.
Odds Ratios and Relative Risks
There are the following relations between the OR and the RR:
- If \(\pi_0=\pi_1\) then \(\mbox{OR}= \mbox{RR}= 1\).
- OR and RR always go in the same direction (\(<1\) or \(>1\)).
- If \(<1\), then \(\mbox{OR}< \mbox{RR}\).
- If \(>1\), then \(\mbox{OR}> \mbox{RR}\).
- Rare disease assumption: If disease risks \(\pi_0\) and \(\pi_1\) are small, then \(\mbox{OR}\approx \mbox{RR}\).
The function Epi::twoby2() computes the RR, OR (in two versions)
and ARR (probability difference).
The second version of the odds ratio is the conditional Maximum Likelihood
estimate under a hypergeometric likelihood function.
There is no closed-form expression for this estimate, which
may explain why it is rarely used, but it is compatible to the
\(P\)-value from Fisher’s exact test (denoted here as Exact P-value).
## 2 by 2 table analysis:
## ------------------------------------------------------
## Outcome : dead
## Comparing : APSAC vs. Heparin
##
## dead alive P(dead) 95% conf. interval
## APSAC 9 153 0.0556 0.0292 0.1033
## Heparin 19 132 0.1258 0.0817 0.1889
##
## 95% conf. interval
## Relative Risk: 0.4415 0.2062 0.9455
## Sample Odds Ratio: 0.4087 0.1788 0.9340
## Conditional MLE Odds Ratio: 0.4098 0.1576 0.9893
## Probability difference: -0.0703 -0.1378 -0.0063
##
## Exact P-value: 0.0459
## Asymptotic P-value: 0.0338
## ------------------------------------------------------Compatible \(P\)-values can be obtained for each of these effect estimates and the corresponding standard error. They will be similar, but not identical:
## transform normal test statistic z to two-sided p-value
z2p <- function(z) return(2*(1-pnorm(abs(z))))
z <- c(arr/se.arr, log(rr)/se.log.rr, log(or)/se.log.or)
names(z) <- c("risk difference", "log relative risk", "log odds ratio")
pvalues <- z2p(z)
biostatUZH::formatPval(pvalues)## risk difference log relative risk log odds ratio
## "0.03" "0.035" "0.028"The one for OR is called Asymptotic P-value in twoby2().
Absolute and relative effect measures
Let us consider an example of an RCT with \[\begin{eqnarray*} \mbox{death risk} &= & \left\{ \begin{array}{rl} 0.3\% & \mbox{in the placebo group} \\ 0.1\% & \mbox{in the treatment group} \end{array} \right. \end{eqnarray*}\] Then we have \(\mbox{ARR}=0.2\%= 0.002\) and \(\mbox{NNT}=500\), so there is a very small absolute effect of treatment. However, we have \(\mbox{RR}=1/3\) and \(\mbox{RRR}= 2/3 = 67\%\), so there is a large relative effect of treatment. We cannot transform absolute to relative effect measures (and vice versa) without knowledge of the underlying risks.
8.2 Adjusting for baseline observations
For binary outcomes, adjusting for baseline variables is usually done using logistic regression and will produce adjusted odds ratios. Alternatively, the Mantel-Haenszel method (MH) can be used, which gives a weighted average of strata-specific odds ratios. The MH method can also be applied to strata-specific risk ratios. However, adjustment for continuous variables using MH is only possible after suitable categorization.
8.2.1 Logistic regression
Example 8.3 The PUVA trial (Gordon et al, 1999) compares PUVA
(oral methoxsalen followed by UVA exposure) versus TL-01 lamp therapy for treatment of
psoriasis. The primary outcome is clearance of psoriasis (yes/no)
at or before the end of the treatment.
The treatment allocation used RPBs stratified according to whether predominant
plaque size was large or small. This ensures a balanced distribution
in treatment arms (29:22 vs. 28:21).
## plaqueSize treatment cleared total
## 1 Small TL-01 23 29
## 3 Small PUVA 25 28
## 2 Large TL-01 9 22
## 4 Large PUVA 16 21The unadjusted analyis can be performed as follows:
m1 <- glm(cbind(cleared, total-cleared) ~ treatment,
data=puva, family=binomial)
knitr::kable(tableRegression(m1, latex = FALSE, xtable = FALSE))| Odds Ratio | 95%-confidence interval | \(p\)-value | |
|---|---|---|---|
| treatmentTL-01 | 0.33 | from 0.12 to 0.82 | 0.021 |
The strata-specific estimates are obtained using:
m2Small <- glm(cbind(cleared, total-cleared) ~ treatment,
subset=(plaqueSize=="Small"), data=puva, family=binomial)| Odds Ratio | 95%-confidence interval | \(p\)-value | |
|---|---|---|---|
| treatmentTL-01 | 0.46 | from 0.09 to 1.96 | 0.31 |
m2Large <- glm(cbind(cleared, total-cleared) ~ treatment,
subset=(plaqueSize=="Large"), data=puva, family=binomial)
knitr::kable(tableRegression(m2Large, latex = FALSE, xtable = FALSE))| Odds Ratio | 95%-confidence interval | \(p\)-value | |
|---|---|---|---|
| treatmentTL-01 | 0.22 | from 0.05 to 0.77 | 0.023 |
Finally, the adjusted analysis with logistic regression is:
| Odds Ratio | 95%-confidence interval | \(p\)-value | |
|---|---|---|---|
| treatmentTL-01 | 0.30 | from 0.10 to 0.78 | 0.017 |
| plaqueSizeLarge | 0.24 | from 0.09 to 0.61 | 0.004 |
The adjusted treatment effect is \(\widehat{\mbox{OR}} = 0.30\) with 95% CI from \(0.10\) to \(0.78\). Logistic regression also quantifies the effect of the variable used for adjustment, here plaque size, and gives a better model fit:
## Analysis of Deviance Table
##
## Model 1: cbind(cleared, total - cleared) ~ treatment
## Model 2: cbind(cleared, total - cleared) ~ treatment + plaqueSize
## Resid. Df Resid. Dev Df Deviance
## 1 2 9.5077
## 2 1 0.5426 1 8.96518.3 Ordinal outcomes
Many clinical trials yield outcomes on an ordered categorical scale such as “very good”, “good”, “moderate”, “poor”. Such data can be analysed using proportional odds regression techniques.
Suppose that we have \(k = 1, \ldots K\) categories and define the odds ratio
OR\(_k\) at each cut-off point \(k = 1, \ldots K - 1\) via
\[
\text{OR}_k = \frac{\operatorname{\mathsf{Pr}}(Y_\text{A} \le k)/\operatorname{\mathsf{Pr}}(Y_\text{A} > k)}
{\operatorname{\mathsf{Pr}}(Y_\text{B} \le k)/\operatorname{\mathsf{Pr}}(Y_\text{B} > k)},
\]
where \(Y_\text{A}\) and \(Y_\text{B}\) denote the outcomes from treatment group A and B, respectively.
The proportional odds logistic regression model assumes
\(\text{OR}_k = \text{OR}\) for all \(k = 1,\dots, K-1\).
Sample size methods are available in the R function
Hmisc::posamsize().
Example 8.4 A clinical trial has been conducted to compare the drug auranofin with placebo for the treatment of rheumatoid arthritis (Bombardier et al, 1986; Lipsitz et al, 1994). Patients were randomized to one of the two treatments for the entire study. The ordered response is the self-assessment of arthritis classified as (1) poor, (2) fair, or (3) good. Of the 303 randomized patients, 299 were observed at both baseline and follow-up.
Here is what the data at baseline and at follow-up looks like:
##
## Placebo Auranofin Sum
## Poor 46 49 95
## Fair 69 68 137
## Good 33 34 67
## Sum 148 151 299## by
## Placebo Auranofin Sum
## Poor 44 18 62
## Fair 50 77 127
## Good 54 56 110
## Sum 148 151 299The cumulative odds ratios are
t <- table(arthritis$followup, by=arthritis$treatment)
x1 <- t[1,]
n <- apply(t, 2, sum)
confIntOddsRatio(x=x1, n=n)## lower.Placebo Odds Ratio.Placebo upper.Placebo
## 1.706339 3.126068 5.727058## lower.Placebo Odds Ratio.Placebo upper.Placebo
## 0.6412333 1.0261209 1.6420295and so, the proportional odds assumption is questionable.
A proportional odds logistic regression yields:
library(MASS)
## polr: proportional odds logistic regression
polr1 <- polr(followup ~ treatment, data=arthritis)
print(s1 <- summary(polr1))##
## Re-fitting to get Hessian## Call:
## polr(formula = followup ~ treatment, data = arthritis)
##
## Coefficients:
## Value Std. Error t value
## treatmentAuranofin 0.4114 0.2173 1.893
##
## Intercepts:
## Value Std. Error t value
## Poor|Fair -1.1310 0.1791 -6.3148
## Fair|Good 0.7692 0.1710 4.4980
##
## Residual Deviance: 628.9683
## AIC: 634.9683## odds ratio is exp of coefficient
CoefTable <- s1$coefficients
printWaldCI(theta=CoefTable[1,"Value"], se=CoefTable[1,"Std. Error"], FUN=exp)## Effect 95% Confidence Interval P-value
## [1,] 1.509 from 0.986 to 2.310 0.058Adjusting for baseline gives:
library(MASS)
## polr: proportional odds logistic regression
polr2 <- polr(followup ~ treatment + baseline, data=arthritis)
print(s2 <- summary(polr2))##
## Re-fitting to get Hessian## Call:
## polr(formula = followup ~ treatment + baseline, data = arthritis)
##
## Coefficients:
## Value Std. Error t value
## treatmentAuranofin 0.5066 0.2289 2.213
## baselineFair 0.5192 0.2546 2.039
## baselineGood 2.5427 0.3631 7.003
##
## Intercepts:
## Value Std. Error t value
## Poor|Fair -0.5137 0.2397 -2.1431
## Fair|Good 1.6665 0.2622 6.3559
##
## Residual Deviance: 567.8201
## AIC: 577.8201## odds ratio is exp of coefficient
CoefTable <- s2$coefficients
printWaldCI(theta=CoefTable[1,"Value"],
se=CoefTable[1,"Std. Error"], FUN=exp)## Effect 95% Confidence Interval P-value
## [1,] 1.66 from 1.060 to 2.600 0.027The second model (polr2) has a better model fit than the first (polr1):
## Likelihood ratio tests of ordinal regression models
##
## Response: followup
## Model Resid. df Resid. Dev Test Df
## 1 treatment 296 628.9683
## 2 treatment + baseline 294 567.8201 1 vs 2 2
## LR stat. Pr(Chi)
## 1
## 2 61.14821 5.273559e-14We can now compare observed and fitted counts for each covariate combination and use a \(\chi^2\)-goodness-of-fit tests:
| Observed | Fitted | Observed | Fitted | Observed | Fitted | |
|---|---|---|---|---|---|---|
| Auranofin, Poor baseline | 8 | 13.0 | 27 | 24.3 | 14 | 11.7 |
| Auranofin, Fair baseline | 9 | 12.0 | 42 | 32.5 | 17 | 23.5 |
| Auranofin, Good baseline | 1 | 0.9 | 8 | 5.9 | 25 | 27.2 |
| Placebo, Poor baseline | 25 | 17.2 | 12 | 21.5 | 9 | 7.3 |
| Placebo, Fair baseline | 16 | 18.1 | 34 | 34.3 | 19 | 16.6 |
| Placebo, Good baseline | 3 | 1.5 | 4 | 8.2 | 26 | 23.3 |
## [1] 0.04222167There is some evidence for poor model fit (\(p=0.042\)).
8.4 Additional references
Relevant references for this chapter are in particular Chapters 13 “The Analysis of Cross-Tabulations” and 15.10 “Logistic Regression” in Bland (2015) as well as Chapter 7.1–7.4 “Further Analysis: Binary Data” in Matthews (2006). The use of odds ratios is discussed in Sackett et al (1996) and Altman et al (1998). Studies where the methods from this chapter are used in practice are for example Heal et al (2009), Fagerström et al (2010) and Vadillo-Ortega et al (2011).