Kapitel 12 bedingte Wahrscheinlichkeiten

In Kapitel 11 wurde die Definition der stochastischen Unabhängigkeit eingeführt. Sind die Ereignisse \(A\) und \(B\) unabhängig, so liefern Informationen bezüglich des Ereignises \(A\) keine verwertbaren Informationen bezüglich des Ausgangs von Ereignis \(B\). Den Ausgangspunkt bildet der Wahrscheinlichkeitsraum \((\Omega, S, W)\), wobei die Ereignisse \(A\) und \(B\) in der \(\sigma\)-Algebra \(S\) enthalten sind.
Beispiel:
Betrachtet werde ein Würfelwurf, \(\Omega=\{1,2,3,4,5,6\}\), mit den Ereignissen \(A=\{2,5\}\) und \(B=\{2,4,6\}\). Nach der klassischen Wahrscheinlichkeitsrechnung gilt somit \(W(A)=\frac{2}{6}=\frac{1}{3}\) und \(W(B)=\frac{3}{6}=\frac{1}{2}\). Wegen \(A\cap B=\{2\}\) gilt: \(W(A\cap B)=\frac{1}{6}\).
Die Ereignisse \(A\) und \(B\) sind unabhängig, da \(W(A\cap B)=W(A)\cdot W(B)\).
Selbst wenn feststeht, dass das Ereignis \(B\) eintreten wird, so verändert dies für die unabhängigen Ereignisse \(A\) und \(B\) nicht die Eintrittswahrscheinlichkeit von \(A\). Mit der Festlegung auf das Eintreten von \(B\) reduzieren sich die möglichen Resultate \(\Omega\) auf \(B\).
Es können somit nur noch jene Resultate von \(A\) eintreten, welche einen Schnitt mit \(B\) aufweisen. Im Beispiel ist dies \(A\cap B=\{2\}\).
Die Wahrscheinlichkeit für \(A\) unter der Bedingung \(B\) lautet dann: \[W(A|B)=\frac{n[G_{A\cap B}]}{n[G_B]}=\frac{1}{3}\] Die Bedingung wird im Ausdruck immer hinter dem Betragsstrich notiert.
Betrachtet werde neben den Ereignissen \(A\) und \(B\) das Ereignis \(C=\{4,5,6\}\).
Die Wahrscheinlichkeit für \(C\) unter der Bedingung \(B\) lautet dann: \[W(C|B)=\frac{n[G_{C\cap B}]}{n[G_B]}=\frac{2}{3}\] Das Eintreten von \(C\) ist somit abhängig vom Eintreten von \(B\), da sich die Eintrittswahrscheinlichkeit für \(C\) von \(W(C)=\frac{1}{2}\) durch die Bedingung auf \(W(C|B)=\frac{2}{3}\) ändert.

12.1 Definition bedingte Wahrscheinlichkeit

Stammen die Ereignisse \(A\) und \(B\) aus der \(\sigma\)-Algebra \(S\) eines Wahrscheinlichkeitsraums \((\Omega, S, W)\), so wird die Wahrscheinlichkeit für \(A\) unter der Bedingung \(B\) notiert als: \[W(A|B)=\frac{W(A\cap B)}{W(B)}\]

Durch die Bedingung \(B\) wird mit \(W(\cdot|B)\) eine neue Wahrscheinlichkeitsfunktion festgelegt, welche für \(W(B)>0\) ebenfalls den Axiomen von Kolmogorov folgt:

• \(W(A|B)\geq 0\), für jedes \(A \in S\)
  
• \(W(\cup_i A_i|B)=\sum_i W(A_i|B)\), für \(A_i \in S, \ \mbox{welche paarweise disjunkt sind}\)
• \(W(\Omega|B)=1\)

Schließlich erhält man den Wahrscheinlichkeitsraum \((\Omega, S, W(\cdot|B))\) für welchen in der auf \(B\) bedingten Betrachtung auch die in Kapitel 11.2.3 genannten Folgerungen aus den Axiomen gelten.

bedingte Wahrscheinlichkeiten unabhängiger Ereignisse
Für unabhängige Ereignisse \(A\) und \(B\) gilt wegen \(W(A\cap B)=W(A)\cdot W(B)\) grundsätzlich: \[W(A| B)=\frac{W(A\cap B)}{W(B)}=\frac{W(A)\cdot W(B)}{W(B)}=W(A)\] Außerdem gilt wegen \(W(A\cap B)=W(B\cap A)\) für die unabhängigen Ereignisse \(A\) und \(B\): \[W(B| A)=\frac{W(B\cap A)}{W(A)}=\frac{W(A)\cdot W(B)}{W(A)}=W(B)\] Die bedingte Wahrscheinlichkeit entspricht für unabhängige Ereignisse also der unbedingten Wahrscheinlichkeit. Dies ist insofern plausibel, als dass das Eintreten von \(A\) nicht vom Eintreten von \(B\) beeinflusst wird und umgekehrt, falls \(A\) und \(B\) unabhängig sind.

Fortsetzung Beispiel Tetraeder aus Kapitel 11

Gehen wir nun erneut von dem bekannten Tetraeder (4 Seiten) aus, welcher gewürfelt werden soll.
Zur Erinnerung:
Eine Seite ist blau, eine Seite ist gelb, eine Seite ist rot und die vierte Seite ist mit allen drei Farben (blau, gelb und rot) gefärbt worden.

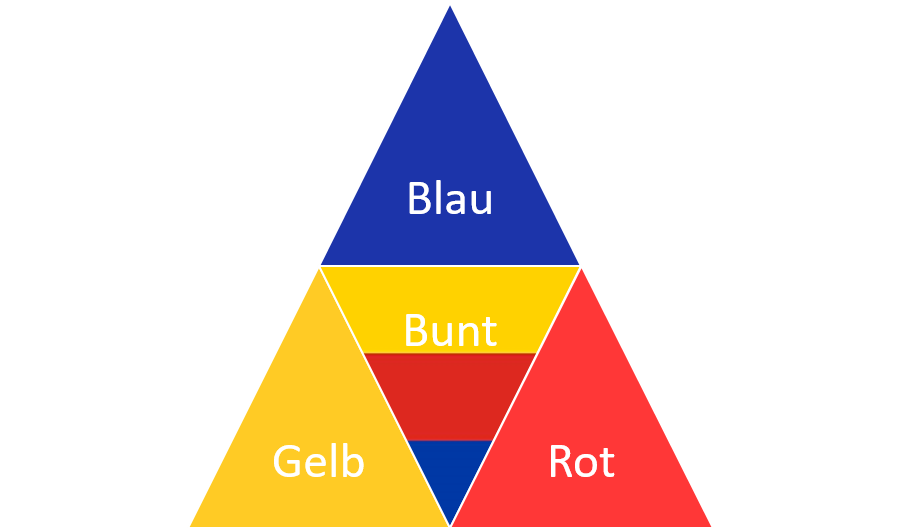
12.1: gefärbter Tetraeder

Betrachtet werden die Ereignisse A, B und C:
A: Es wird eine Seite gewürfelt, welche blaue Farbe aufweist.
B: Es wird eine Seite gewürfelt, welche gelbe Farbe aufweist.
C: Es wird eine Seite gewürfelt, welche rote Farbe aufweist.

Hinweis: Die folgende Abbildung veranschaulicht das Ereignis \(B\), welches die Bedingung darstellt.

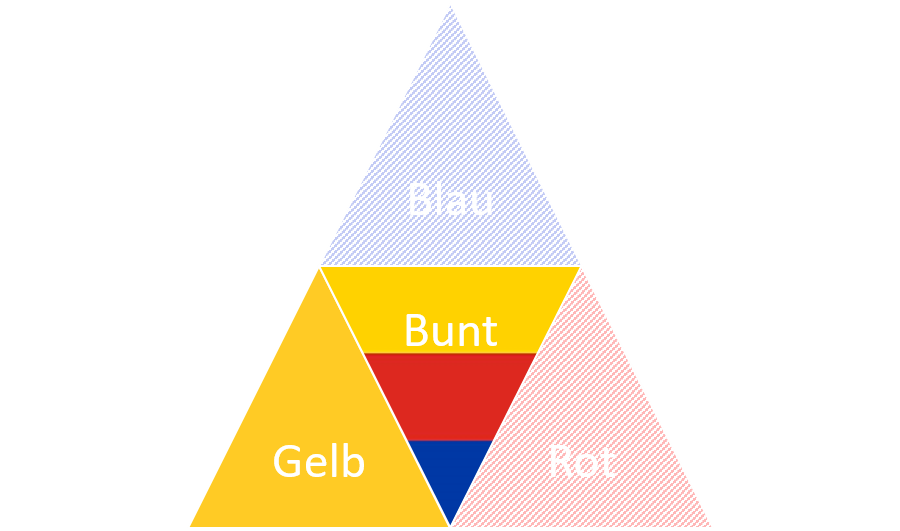
12.2: Ereignis B

Hinweis: Die folgende Abbildung veranschaulicht das Ereignis \(B\cap C\), welches die Bedingung darstellt.

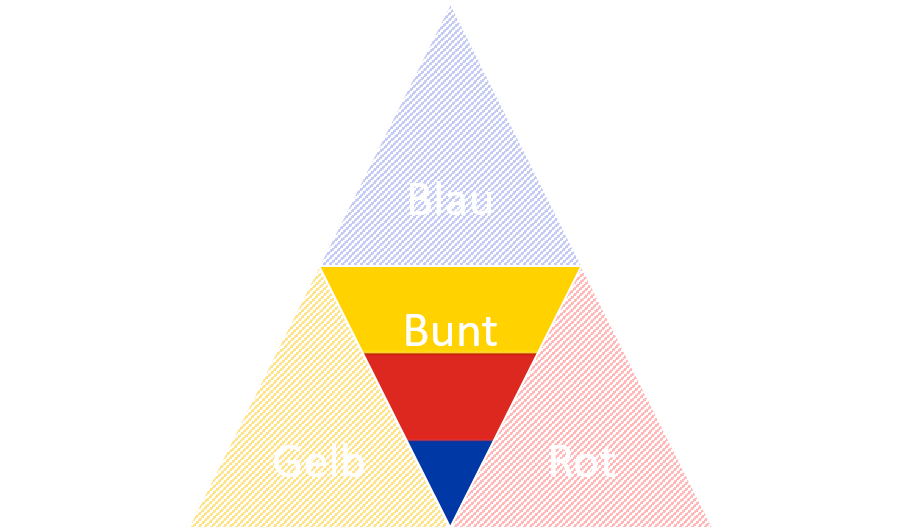
12.3: Ereignis B

12.2 Fallbeispiel HIV-Test

Ein HIV-Test entdeckt eine Infektion mit einer Wahrscheinlichkeit von 99,8%. Der Test ist negativ mit einer Wahrscheinlichkeit von 99%, falls jemand nicht infiziert ist. Ferner kann davon ausgegangen werden, dass in Deutschland 0,1% der sexuell aktiven Bevölkerung tatsächlich infiziert ist.
(Angaben aus dem Buch von Walter Krämer und Götz Trenkler: Lexikon der populären Irrtümer (Taschenbuchausgabe München 2002 S. 17f.)).

Mit welcher Wahrscheinlichkeit ist eine Person nicht infiziert, falls das Testergebnis positiv ausfällt?

Es ist zunächst zu klären, welche Merkmale betrachtet werden.
In der Aufgabenstellung sind dies die Merkmale Infektion und Testergebnis. Im folgenden werden für die zugehörigen Merkmalsausprägungen folgende Ereignisse festgelegt:

• \(I\) bedeutet, dass eine Infektion vorliegt.
• \(\overline{I}\) bedeutet, dass keine Infektion vorliegt.
• \(P\) bedeutet, dass das Testergebnis positiv ist.
• \(\overline{P}\) bedeutet, dass das Testergebnis negativ ist.

Aus dem Aufgabentext können dann folgende Wahrscheinlichkeiten gelesen werden:

• \(W(P|I)=0,998\): Sofern der Test bei Vorliegen einer Infektion, diese auch erkennt, zeigt er ein positives Testergebnis an. Mit einer Wahrscheinlichkeit von 99,8% tritt also \(P\) ein, falls \(I\) gilt, die getestete Person also infiziert ist.
• \(W(\overline{P}|\overline{I})=0,99\): Mit einer Wahrscheinlichkeit von 99% tritt ein negatives Testergebnis \(\overline{P}\) ein, falls die getestete Person nicht infiziert ist, also \(\overline{I}\) gilt.
• \(W(I)=0,001\): Sofern 0,1% der Grundgesamtheit, welche hier die sexuell aktive Bevölkerung darstellt, infiziert sind, ergibt sich bei zufälliger Auswahl aus der Grundgesamtheit eine Wahrscheinlichkeit von 0,1% für eine infizierte Person, also \(I\).

Im Hinblick auf die Fragestellung gilt:

• \(W(\overline{I}|P)\) Durch die Festlegung auf positiv getestete Personen ist \(P\) die Bedingung und \(\overline{I}\) das Ereignis, für welches die Wahrscheinlichkeit unter der Bedingung \(P\) zu ermitteln ist.

Die Bestimmung der Ereignisse und Zuordnung der Wahrscheinlichkeiten wird nochmal im folgenden Video ausführlich beschrieben:

Im Folgenden werden zur Beantwortung der Fragestellung drei Lösungswege vorgestellt:

12.2.1 Lösung mittels klassischer Wahrscheinlichkeitsrechnung

Die Ausgangsbasis bildet eine willkürlich groß gewählte Grundgesamtheit der sexuell aktiven Bevölkerung, welche nach den in der Aufgabenstellung genannten Merkmalen abgegrenzt werden kann. Die Zahl sollte so groß gewählt werden, dass sich nach vorgenommener Abgrenzung ausschließlich ganzzahlige Werte ergeben. Für die Darstellung empfiehlt sich ein Baumdiagramm, wie in Abbildung 12.4 dargestellt.
Im Folgenden wird von einem Wert von 1.000.000 ausgegangen. Die Bevölkerung kann dann in infizierte \(I\) und nicht infizierte \(\overline{I}\) Personen aufgeteilt werden. Innerhalb der beiden Gruppen erfolgt mit Hilfe der beiden bedingten Wahrscheinlichkeiten \(W(P|I)\) und \(W(\overline{P}|\overline{I})\) eine weitere Untergliederung in Personen mit positivem Test (\(P\)) und negativen Test (\(\overline{P}\)).
Die gesuchte Wahrscheinlichkeit \(W(\overline{I}|P)\) kann dann mit der klassischen Wahrscheinlichkeitsrechnung ermittelt werden. Dazu wird mit Blick auf Abbildung 12.4 die Zahl der Personen mit positivem Test benötigt, also \(n[G_P]=998+9990\) und die Anzahl der Personen, welche ein positives Testergebnis haben und nicht infiziert sind, also \(n[G_{\overline{I}\cap P}]=9990\). Es gilt: \[W(\overline{I}|P)=\frac{Anzahl\ nicht \ infizierter \ Personen \ mit\ positivem\ Test}{Anzahl\ der\ Personen\ mit\ positivem\ Test}=\frac{9990}{998+9990}\approx 0,91\]

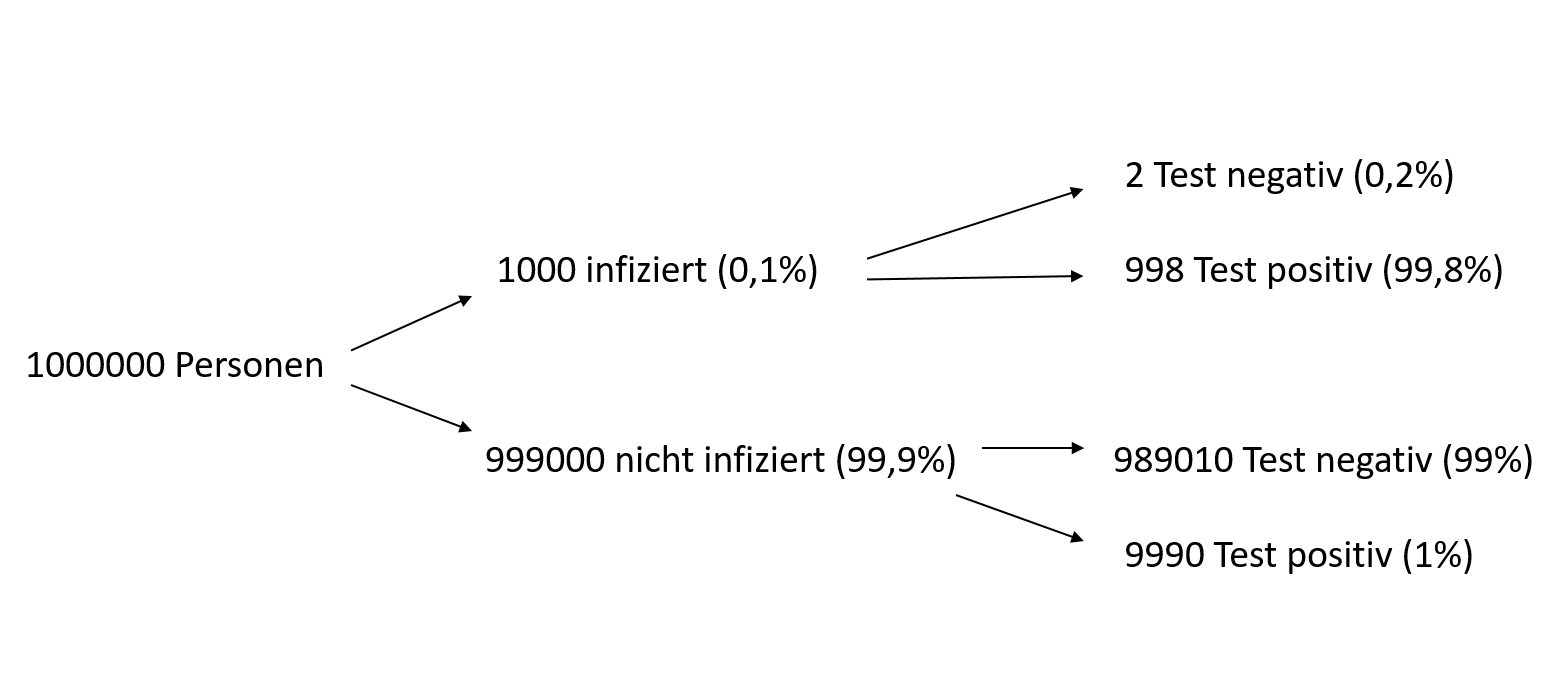
12.4: Baumdiagramm

12.2.2 Lösung mittels Kontingenztabellen

Die Wahrscheinlichkeiten zu den beiden Merkmalen “Infektion” und “Testergebnis” lassen sich mit Ihren Ausprägungen \(I\), \(\overline{I}\), \(P\) und \(\overline{P}\), wie in Abbildung 12.5 durch eine Kontingenztabelle veranschaulichen. In der letzten Zeile und der letzten Spalte finden sich die Randwahrscheinlichkeiten. Im Inneren der Tabelle werden die Wahrscheinlichkeiten für den Schnitt der betrachteten Ereignisse notiert. Ereignis und Gegenereignis sind jeweils disjunkt und bilden somit eine Zerlegung von \(\Omega\). Gemäß der 6. Folgerung aus den Axiomen entspricht die zeilenweise- und spaltenweise Summe der Schnittwahrscheinlichkeiten somit der jeweiligen Randwahrscheinlichkeit. Es gilt somit: \[\begin{align*} W(I)&=W(P\cap I)+W(\overline{P}\cap I), \ \ \mbox{wegen} \ \ P\cap \overline{P}=\emptyset, \ \ P\cup\overline{P}=\Omega\\ W(\overline{I})&=W(P\cap \overline{I})+W(\overline{P} \cap \overline{I}), \ \ \mbox{wegen} \ \ P\cap \overline{P}=\emptyset, \ \ P\cup\overline{P}=\Omega\\ W(P)&=W(P\cap I)+W(P \cap \overline{I}), \ \ \mbox{wegen} \ \ I\cap \overline{I}=\emptyset, \ \ I\cup\overline{I}=\Omega\\ W(\overline{P})&=W(\overline{P}\cap I)+W(\overline{P}\cap \overline{I}), \ \ \mbox{wegen} \ \ I\cap \overline{I}=\emptyset, \ \ I\cup\overline{I}=\Omega \end{align*}\]

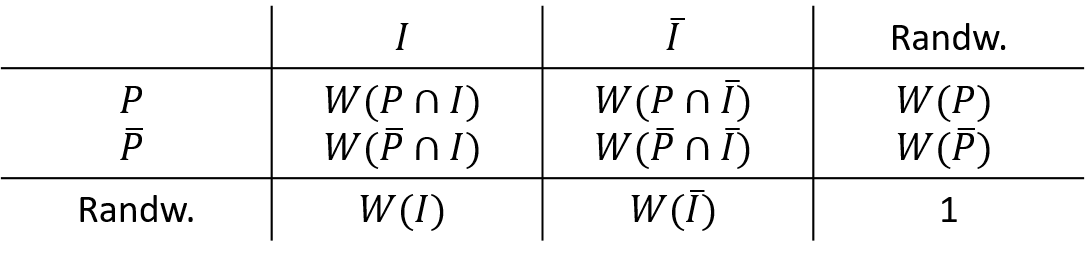
12.5: Kontingenztabelle Wahrscheinlichkeiten 1

Nun kann aus den Informationen der Aufgabenstellung nur \(W(I)=0,001\) direkt in die Kontingenztabelle übernommen werden, denn \(W(P|I)=0,998\) und \(W(\overline{P}|\overline{I})=0,99\) sind bedingte Wahrscheinlichkeiten.
Schauen wir zunächst auf \(W(P|I)\). Aus der Definition der bedingten Wahrscheinlichkeit folgt \(W(P|I)=\frac{W(P\cap I)}{W(I)}\). Somit kann \(W(P\cap I)\) durch Umstellung der Gleichung einfach berechnet werden und in die Kontingenztabelle übernommen werden: \[W(P\cap I)=W(P|I)\cdot W(I)=0,998\cdot 0,001=0,000998\] Aus \(W(I)=0,001\) folgt \(W(\overline{I})=1-W(I)=0,999\).
Somit kann auch \(W(\overline{P}|\overline{I})\) wie folgt ermittelt und in die Kontingenztabelle übernommen werden: \[W(\overline{P}\cap \overline{I})=W(\overline{P}|\overline{I})\cdot W(\overline{I})=0,99\cdot 0,999=0,989010\] Abbildung 12.6 zeigt die Kontingenztabelle mit den so eben berechneten Wahrscheinlichkeiten.

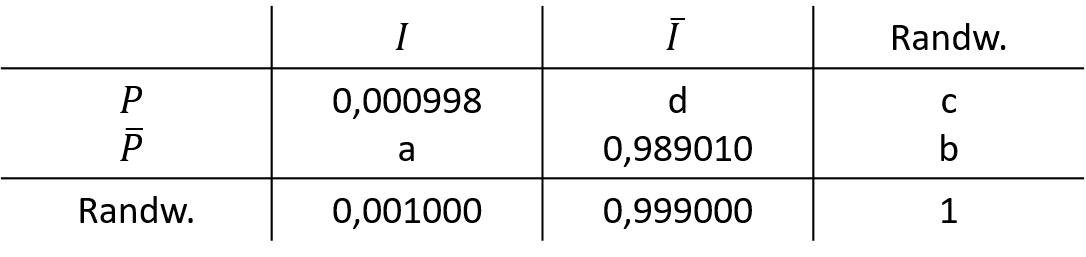
12.6: Kontingenztabelle Wahrscheinlichkeiten 2

Die übrigen Wahrscheinlichkeiten lassen sich aus der Kenntnis, dass die Summe der gemeinsamen zeilen- spaltenweisen Wahrscheinlichkeiten den zugehörigen Randwahrscheinlichkeiten entspricht, in der Reihenfolge \(a\), \(b\), \(c\), \(d\) bestimmen. So erhält man schließlich die in Abbildung 12.7 dargestellte Kontingenztabelle.

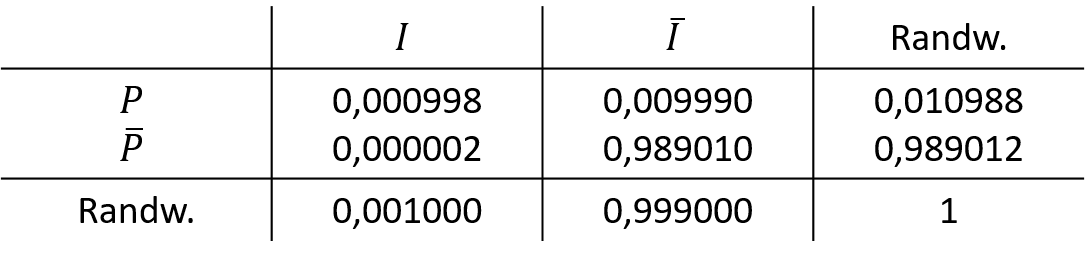
12.7: Kontingenztabelle Wahrscheinlichkeiten 3

Die gesuchte Wahrscheinlichkeit \(W(\overline{I}|P)\) kann somit ganz einfach unter Rückgriff auf die Wahrscheinlichkeiten aus Abbildung 12.7 berechnet werden:

\[W(\overline{I}|P)=\frac{W(P\cap \overline{I})}{W(P)}=\frac{0,009990}{0,010988}\approx 0,91\]

12.2.3 Lösung mit dem Satz von Bayes

Eine weitere Möglichkeit zur Bestimmung von bedingten Wahrscheinlichkeiten stellt der Satz von Bayes dar.
Im Weiteren stellen die Ereignisse der Menge \(\{B_1,B_2,...\}\) aus der \(\sigma\)-Algebra \(S\) des Wahrscheinlichkeitsraums \((\Omega, S, W)\) eine Zerlegung von \(\Omega\) dar. Die Ereignisse sind somit paarweise disjunkt und ihre Vereinigung führt zu \(\Omega\).
Mit dem Satz von Bayes lässt sich aus einer festgelegten a-priori-Wahrscheinlichkeit (ohne Zusatzinformationen) \(W(B_k)\) eine a-posteriori-Wahrscheinlichkeit (mit Zusatzinformationen) \(W(B_k|A)\) berechnen.
Man geht daher der Frage nach, wie sich eine unbedingte Wahrscheinlichkeit durch Berücksichtigung einer Information \(A\) verändert.
Die a-posteriori-Wahrscheinlichkeit \(W(B_k|A), \mbox{ mit }B_k\in \{B_1,B_2,...\}\) kann nach dem Satz von Bayes unter Rückgriff auf die a-priori-Wahrscheinlichkeit \(W(B_k)\) wie folgt ermittelt werden:

\[W(B_k|A)=\frac{W(A|B_k)\cdot W(B_k)}{\sum_i W(A|B_i)\cdot W(B_i)}\]

In der Aufgabenstellung wird die a-posteriori-Wahrscheinlichkeit \(W(\overline{I}|P)\) gesucht.
Die folgenden Wahrscheinlichkeiten sind aus der Aufgabenstellung direkt bekannt:

• \(W(P|I)=0,998\)
• \(W(\overline{P}|\overline{I})=0,99\)
• \(W(I)=0,001\)

Die Ereignisse \(P\) und \(\overline{P}\) bilden analog zur allgemeinen Formulierung mit den Ereignissen \(B_1,B_2,...\) eine Zerlegung von \(\Omega\). Nach dem Satz von Bayes kann \(W(\overline{I}|P)\) somit wie folgt bestimmt werden:

\[W(\overline{I}|P)=\frac{W(P|\overline{I})\cdot W(\overline{I})}{W(P|\overline{I})\cdot W(\overline{I})+ W(P|I)\cdot W(I)}\]

Die a-priori- Wahrscheinlichkeit \(W(\overline{I})\) erschließt sich unmittelbar aus: \[W(\overline{I})=1-W(I)=1-0,001=0,999\]
Für die Berechnung wird allerdings im Zähler und im Nenner mit \(W(P|\overline{I})\) noch die Wahrscheinlichkeit für ein positives Testergebnis bei nicht Vorliegen einer Infektion benötigt. Diese kann einfach ermittelt werden aus: \[W(P|\overline{I})=1-W(\overline{P}|\overline{I})=1-0,99=0,01\] Somit folgt schließlich: \[W(\overline{I}|P)=\frac{W(P|\overline{I})\cdot W(\overline{I})}{W(P|\overline{I})\cdot W(\overline{I})+ W(P|I)\cdot W(I)}=\frac{0,01\cdot 0,999}{0,01\cdot 0,999+0,998\cdot 0,001}\approx 0,91\]

12.3 Antigen-Schnelltests auf SARS-CoV-2 und bedingte Wahrscheinlichkeiten

Das folgende Tool ermöglicht am Beispiel der Mindestvorgaben für Antigen-Schnelltests auf SARS-CoV-2 die automatisierte Erstellung einer Kontingenztabelle sowie die Bestimmung einer bedingten Wahrscheinlichkeit, analog zum Fallbeispiel des HIV-Tests aus Kapitel 12.2.2: