Kapitel 8 Maßzahlen des statistischen Vergleichs

Absolute Zahlenangaben sind oft unanschaulich und isoliert betrachtet wenig aussagefähig. So ist etwa die Zahl der binnen einer Woche in einem Landkreis nachweislich an Covid-19 erkrankten Personen von geringem Aussagegehalt, ohne die Einwohnerzahl des Landkreises zu kennen. Erst wenn man beide Zahlen ins Verhältnis zueinander setzt, erhält man ein interpretierbares relatives Maß. Multipliziert man dieses noch mit 100.000, so erhält man den für politische Entscheidungen richtweisenden Inzidenzwert:

\[Inzidenzwert=\frac{Zahl \ der \ nachweislich \ erkrankten \ Personen \ der \ letzten \ 7 \ Tage}{Einwohnerzahl}\cdot 100.000\]

Maßzahlen können für sachliche, räumliche oder zeitliche Vergleiche gebildet werden. Grundsätzlich wird zwischen Verhältniszahlen und Veränderungszahlen unterschieden.
Bei Querschnittsdaten beziehen sich alle Beobachtungswerte auf ein- und denselben Zeitpunkt oder ein- und dieselbe Zeitperiode. Maßzahlen, die aus Querschnittsdaten gebildet werden, nennt man Verhältniszahlen.
Bei Zeitreihen sind die Beobachtungswerte datiert. Sie liegen also in einer zeitlichen Reihenfolge vor. Die hier gebildeten Maßzahlen sollen die Dynamik der Entwicklung im Zeitablauf veranschaulichen und heißen Veränderungszahlen.

8.1 Verhältniszahlen

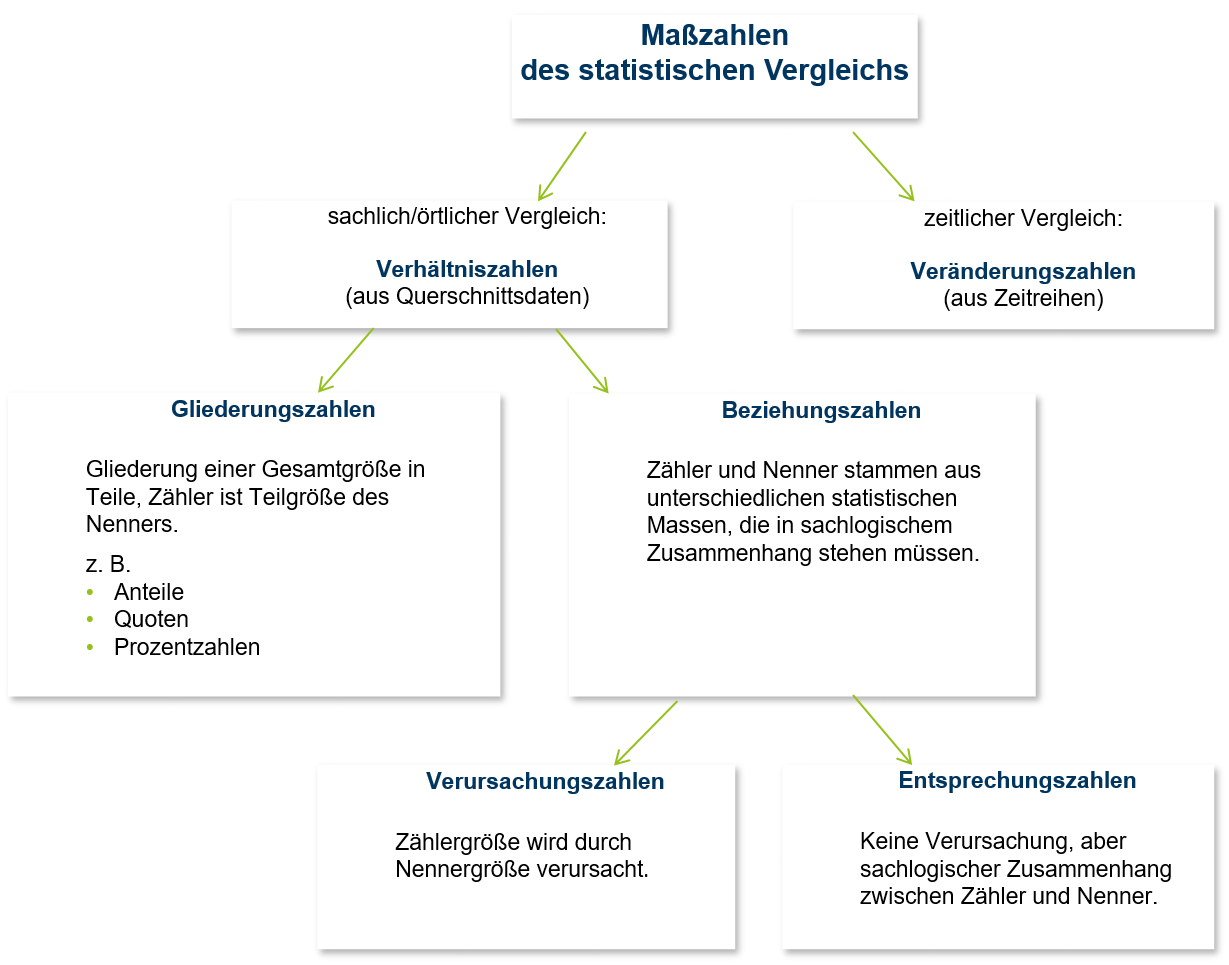
Verhältniszahlen werden nach Gliederungszahlen und Beziehungszahlen unterschieden. Abbildung 8.1 gibt einen Überblick

8.1: Verhältniszahlen

8.1.1 Gliederungszahlen

Gliederungszahlen kennzeichnet, dass diese eine Teilgröße und eine Gesamtgröße ins Verhältnis zueinander setzten. Die Teilgröße ist vollständig in der Gesamtgröße enthalten. Somit liegen Gliederungszahlen immer zwischen 0% und 100%. Beispiele sind die relativen Häufigkeiten \(f_i\).
Gliederungszahlen weisen folgende Eigenschaften auf:

• Teilgröße (Zähler) und Gesamtgröße (Nenner) weisen dieselbe Maßeinheit auf. Die Gliederungszahl ist somit dimensionslos und wird meistens in Prozent angegeben.
• Da die Zählergröße vollständig in der Nennergröße enthalten ist, spricht man auch von einer echten Quote, welche immer zwischen 0% und 100% liegen muss.

Als Beispiel für eine Quote wäre die Durchfallquote bei einer Klausur zu nennen.

8.1.2 Beziehungszahlen

Werden zwei Größen aus unterschiedlichen Grundgesamtheiten zueinander in Beziehung gesetzt, so spricht man von einer Beziehungszahl \(b\).

\[ b=\frac{G_1}{G_2}\]

Zwischen den beiden mit \(G_1\) und \(G_2\) bezeichneten Größen muss ein sachlogischer Zusammenhang existieren. Falls \(G_1\) und \(G_2\) verschiedene Maßeinheiten besitzen, so ist die Beziehungszahl nicht dimensionslos.
Beziehungszahlen werden weiter unterschieden in Verursachungszahlen und Entsprechungszahlen.

Verursachungszahlen

Wird der Zähler einer Beziehungszahl vom Nenner verursacht, so spricht man von einer Verursachungszahl.
Ein Beispiel ist das durchschnittliche Steueraufkommen: \[durchschnittliches \ Steueraufkommen=\frac{Steueraufkommen}{Wohnbevölkerung}\] Andernfalls spricht man von einer Entsprechungszahl

Entsprechungszahl

Ein Beispiel ist die Bevölkerungsdichte \[Bevölkerungsdichte=\frac{Einwohnerzahl}{Fläche}\]

>

8.1.3 Mittelung von Verhältniszahlen

Bei der Mittelung von Verhältniszahlen kommen in Abhängigkeit der Informationslage das arithmetische oder das harmonische Mittel zur Anwendung. Grundsätzlich wird mit der Mittelung das Ziel verfolgt, über eine festgelegte Zahl von Merkmalsträgern mit zugehörigen Verhältniszahlen die Zähler und Nennersumme zu ermitteln. Die Mittelung von Verhältniszahlen wurde bereits in Kapitel 3.2.2.2 ausführlich behandelt.

8.2 Veränderungszahlen

Die meisten Veränderungszahlen kommen ebenfalls durch die Bildung von Verhältnissen zustande, jedoch nicht ausschließlich. In jedem Fall werden zur Bildug von Veränderungszahlen zwei Zeitreihenwerte aus unterschiedlichen Zeitpunkten (für Bestandsgrößen) bzw. Zeitperioden (für Stromgrößen) herangezogen. Abbildung 8.2 gibt einen Überblick über alle Veränderungszahlen, welche im Folgenden behandelt werden.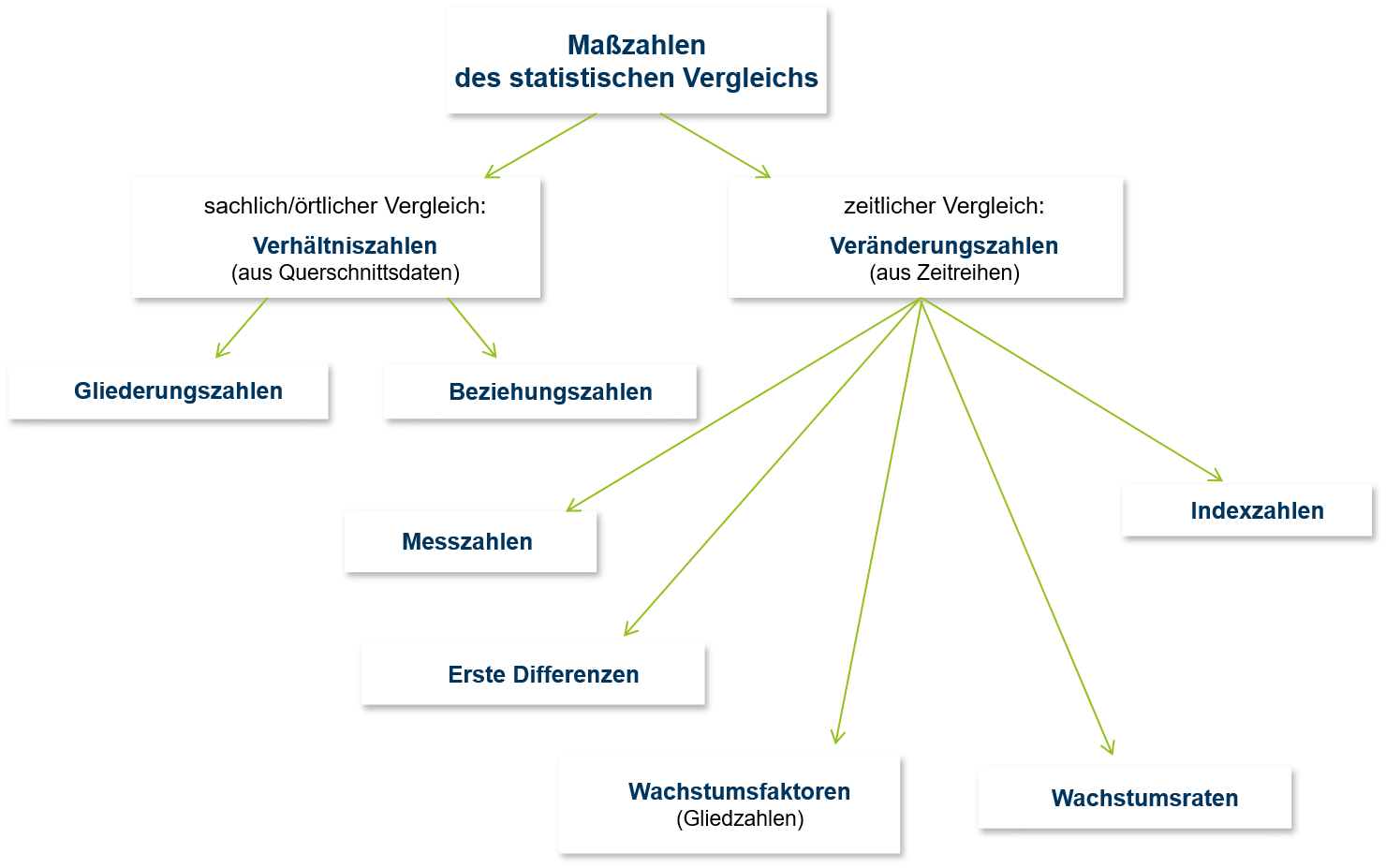

8.2: Veränderungszahlen

>

8.2.1 mögliche Eigenschaften von Veränderungszahlen

Mit \(v_{t_1,t_2}\) wird allgemein die Veränderungszahl bezeichnet, welche aus den Zeitreihenwerten \(x_{t_1}\) und \(x_{t_2}\) gebildet wird, also \[v_{t_1,t_2}(x_{t_1},x_{t_2})\]
Im Folgenden liegen die \(n+1\) Zeitreihenwerte \(x_0\) bis \(x_n\) vor. Je nach Konstruktion von \(v_{t_1,t_2}\) sind folgende drei Eigenschaften möglich, welche in bestimmten Fällen das Arbeiten mit Veränderungszahlen vereinfachen:

• Symmetrie: Falls \(v_{t-1,t}=-v_{t,t-1}\), so bezeichnet man die Veränderungszahl als symmetrisch.

• Additivität: Falls \(\sum_{t=1}^nv_{t-1,t}=v_{0,n}\), so bezeichnet man die Veränderungszahl als additiv.

• Multiplikativität: Falls \(\prod_{t=1}^nv_{t-1,t}=v_{0,n}\), so bezeichnet man die Veränderungszahl als multiplikativ.

Beispiel:
Für die erste Differenz \(\Delta x_t=x_t-x_{t-1}\) gilt:

• Symmetrie, da \(-\Delta x_t=x_{t-1}-x_{t}\)
• Additivität, da \(\sum_{t=1}^n\Delta x_t=\sum_{t=1}^n(x_t-x_{t-1})=x_1-x_0+x_2-x_1+...+x_n-x_{n-1}=x_n-x_0\)
• keine Multiplikativität, da \(\prod_{t=1}^n\Delta x_t=(x_1-x_{0})\cdot (x_2-x_1)\cdot...\cdot(x_n-x_{n-1})\neq x_n-x_0\)

8.2.2 erste Differenzen

Die erste Differenz wird definiert als: \[\Delta x_t=x_t-x_{t-1}, \ \ t \in \{1,..,n\}\] Auf die Eigenschaften von \(\Delta x_t\) (Symmetrie und Additivität) wurde bereits eingegangen.
Der Zeitreihenwert \(x_t\) kann rekursiv als \(x_t=x_{t-1}+\Delta x_t\) berechnet werden.
\(\Delta x_t\) besitzt dieselbe Dimension, wie die Zeitreihenwerte \(x_t\).
Erste Differenzen finden beispielsweise bei der Betrachtung von Aktienkursen Anwendung. So wird neben dem aktuellen Aktienkurs in Währungsangabe meistens auch die Veränderung (erste Differenz) zum Vortag in Währungsangabe übermittelt. Der aktuelle Kurs der thyssenkrupp AG kann über den folgenden Link aufgerufen werden. Neben dem Kursstand übermittelt das Unternehmen auch die Kursänderung zum Vortag (erste Differenz). Zudem wird mit der Wachstumsrate zum Vortag eine weitere Veränderungszahl angegeben. thyssenkrupp website

lineares Wachstum

Sind die ersten Differenzen zeitunabhängig konstant, \(\Delta x_t=b, \ \ t \ \in \ \{1,...,n\}\), so folgen die Zeitreihenwerte \(x_t\) dem linearen Wachstumsmodell: \[x_t=a+b\cdot t, \ \ \mbox{mit dem konstanten Steigungsmaß} \ \ b \ \ \mbox{und} \ \ a=x_0 \ \ \mbox{als Startwert}\]

Im linearen Wachstumsmodell können die Koeffizienten aus zwei Zeitreihenwerten \(x_{t_1}\) und \(x_{t_2}\) wie folgt bestimmt werden:

\[b=\frac{x_{t_2}-x_{t_1}}{t_2-t_1}, \quad a=\frac{t_2\cdot x_{t_1}-t_1\cdot{x_{t_2}}}{t_2-t_1}\]

Erläuterung zur Berechnungsvorschrift für den Koeffizienten \(a\)

\[\begin{align} x_{t_1}&=a+b\cdot t_1\\ \Leftrightarrow a&=x_{t_1}-b\cdot t_1\\ &\mbox{Einsetzen von } b=\frac{x_{t_2}-x_{t_1}}{t_2-t_1}\\ a&=x_{t_1}-\frac{x_{t_2}-x_{t_1}}{t_2-t_1}\cdot t_1\\ &=\frac{x_{t_1}\cdot (t_2-t_1)}{t_2-t_1} -\frac{t_1 \cdot x_{t_2}-t_1\cdot x_{t_1}}{t_2-t_1}\\ &=\frac{t_2\cdot x_{t_1}-t_1\cdot{x_{t_2}}}{t_2-t_1} \end{align}\]

8.2.3 Messzahlen

Die mit \(m_{b,t}\) bezeichneten Messzahlen drücken das Verhältnis zwischen dem Zeitreihenwert \(x_t\), mit variabler Berichtszeit \(t\), zu einem Zeitreihenwert \(x_b\), mit fester Bezugszeit \(b\), aus: \[m_{b,t}=\frac{x_t}{x_b}\] Die Messzahl kann somit auch als Veränderungsfaktor/Wachstumsfaktor mit festem Bezugszeitpunkt interpretiert werden. Der Bezugswert \(x_b\) wird dabei auch als Basiswert bezeichnet.
Messzahlen bilden die Grundlagen für Indexzahlen, welche zum Beispiel in der Preisstatistik zur Anwendung kommen. Preisindizes stellen gewichtete Mittelwerte von Preismesszahlen dar.
Für die folgenden Preisnotationen für eine Jeanshose sollen die Preismesszahlen zur Basiszeit \(b=0\) bestimmt werden:

\(t\)	0	1	2	3
\(x_t\)	80€	85€	90€	100€

Die Preismesszahlen \(m_{0,t}\) lauten:

\(t\)	0	1	2	3
\(m_{0,0}=\frac{80€}{80€}=1\)	\(m_{0,1}=\frac{85€}{80€}=1,0625\)	\(m_{0,2}=\frac{90}{80}=1,125\)	\(m_{0,3}=\frac{100}{80}=1,25\)

Durch die Quotientenbildung sind Messzahlen dimensionslos.
Messzahlen sind nicht symmetrisch, nicht additiv und auch nicht multiplikativ.

Die folgenden Operationen sind für Messzahlen im Zusammenhang mit Indizes von Bedeutung:

Umbasierung

Mit der Umbasierung wird die rechnerische Umstellung auf eine neue Basiszeit \(s\) bezeichnet.

\[m_{s,t}=\frac{m_{b,t}}{m_{b,s}}=\frac{x_t}{x_b}/\frac{x_s}{x_b}=\frac{x_t}{x_s}\]

Verkettung

Mit der Verkettung wird die Verknüpfung von zwei Messzahlen mit unterschiedlichen Basiszeiten bezeichnet. Um eine Verkettung von zwei Messzahlen durchführen zu können, muss die Basiszeit der einen Messzahl mit der Berichtszeit der anderen Messzahl übereinstimmen.

\[m_{b,t}=m_{b,s}\cdot m_{s,t}=\frac{x_s}{x_b}\cdot \frac{x_t}{x_s}=\frac{x_t}{x_b}\]

Sofern die einzelnen Zeitreihenwerte \(x_b\), \(x_s\) und \(x_t\) vorliegen, scheinen die Umbasierung und Verkettung unnötig zu sein, da die gesuchten Messzahlen aus diesen direkt berechnet werden könnten. Häufig sind dem Anwender jedoch nur die Messzahlen bekannt. Mit der Umbasierung und Verkettung von Messzahlen und Indizes werden wir uns in der folgenden Vorlesung noch intensiver auseinandersetzen.

8.2.4 Wachstumsfaktoren und Wachstumsraten

Wachstumsfaktoren

Wachstumsfaktoren \(q_t\) geben, wie Messzahlen, das Verhältnis zweier Zeitreihenwerte an, mit dem Unterschied, dass im Nenner anstelle des Zeitreihenwertes aus einer fixen Basiszeit immer der Zeitreihenwert aus der dem Berichtzeitpunkt vorangegangenen Zeit steht. \[q_t=\frac{x_t}{x_{t-1}}, \ \ t \ \in \ \{1,...,n\}\] Somit kann \(x_t\) rekursiv bestimmt werden mit \(x_t=q_t\cdot x_{t-1}\).
Die dimensionslosen Wachstumsfaktoren sind nicht symmetrisch und nicht additiv, aber multiplikativ, denn der Gesamtwachstumsfaktor \(q_{0,n}=\frac{x_n}{x_0}\) über \(n\) Perioden kann bestimmt werden als: \[q_{0,n}=\prod_{t=1}^n q_t=\frac{x_1}{x_0}\cdot \frac{x_2}{x_1}\cdot...\cdot \frac{x_{n-1}}{x_{n-2}}\cdot \frac{x_n}{x_{n-1}}=\frac{x_n}{x_0}\]

Wachstumsraten in diskreter Zeit

Die Wachstumsrate \(p_t\) kann wie folgt bestimmt werden: \[p_t=\frac{\Delta x_t}{x_{t-1}}=\frac{x_t-x_{t-1}}{x_{t-1}}\] \(p_t\) gibt somit die Änderung des Zeitreihenwertes in Relation zum Vorperiodenwert an.

Die diskrete Wachstumsrate \(p_t\) kann auch mit Hilfe des Wachstumsfaktors \(q_t\) bestimmt werden, da folgender Zusammenhang vorliegt: \[p_t=\frac{x_t-x_{t-1}}{x_{t-1}}=\frac{x_t}{x_{t-1}}-\frac{x_{t-1}}{x_{t-1}}=q_t-1 \] Die dimensionslosen diskreten Wachstumsraten sind nicht symmetrisch, nicht additiv und auch nicht multiplikativ.

durchschnittlicher Wachstumsfaktor

Als durchschnittlicher Wachstumsfaktor \(\overline{q}\) wird jener Wachstumsfaktor bezeichnet, welcher nach \(n\)-maliger Anwendung von \(x_0\) zu \(x_n\) führt: \[x_0\cdot \left(\overline{q}\right)^n=x_n\] Wegen \(x_0\cdot \prod_{t=1}^n q_t=x_n\) gilt: \[\left(\overline{q}\right)^n=\prod_{t=1}^n q_t\] und somit: \[\overline{q}=\left(\prod_{t=1}^n q_t\right)^\frac{1}{n}\] Der durchschnittliche Wachstumsfaktor \(\overline{q}\) ist somit das geometrische Mittel der Wachstumsfaktoren \(q_1\) bis \(q_n\).

durchschnittliche Wachstumsrate

Die durchschnittliche Wachstumsrate \(\overline{p}\) bezeichnet jene konstante Wachstumsrate, welche über \(n\) Perioden von \(x_0\) zu \(x_n\) führt.
Es gilt somit: \[\overline{p}=\overline {q}-1\]

denn

\[x_0\cdot \underbrace{(1+p_1)}_{q_1}\cdot \underbrace{(1+p_2)}_{q_2} \cdot ... \cdot \underbrace{(1+p_n)}_{q_n}=x_0\cdot \underbrace{\left(1+\overline{p}\right)^n}_{\left(\overline{q}\right)^n}=x_n\] Aufgrund der Multiplikativität der Wachstumsfaktoren \(q_t\) können \(\overline{q}\) und \(\overline{p}\) auch einfach nur mit Hilfe des Startwertes \(x_0\) und des Endwertes \(x_n\) bestimmt werden: \[\overline{q}=\left(\frac{x_n}{x_0}\right)^\frac{1}{n}, \quad \overline{p}=\left(\frac{x_n}{x_0}\right)^\frac{1}{n}-1\]

8.3 exponentielles Wachstumsmodell

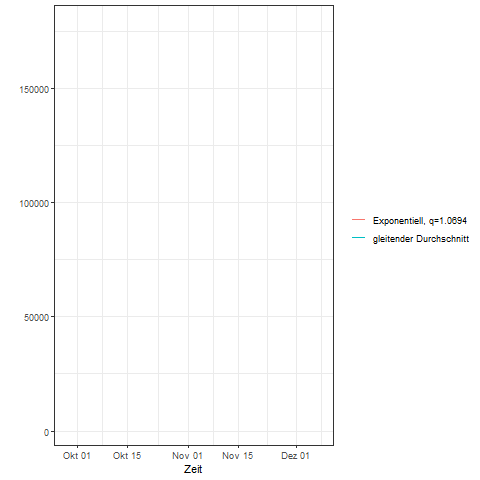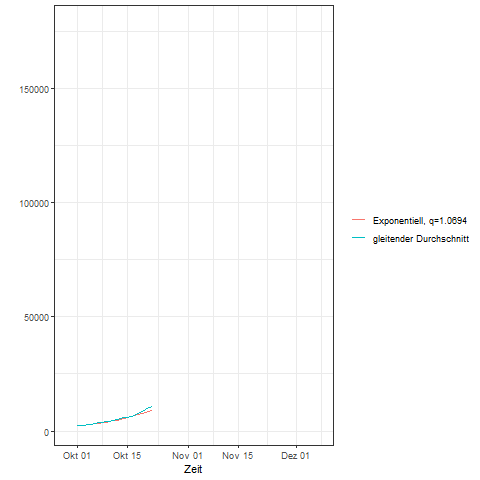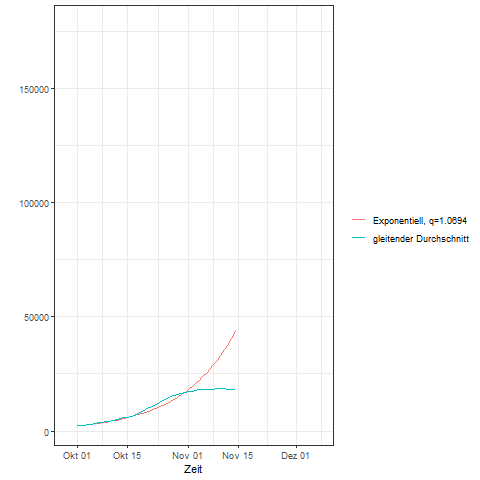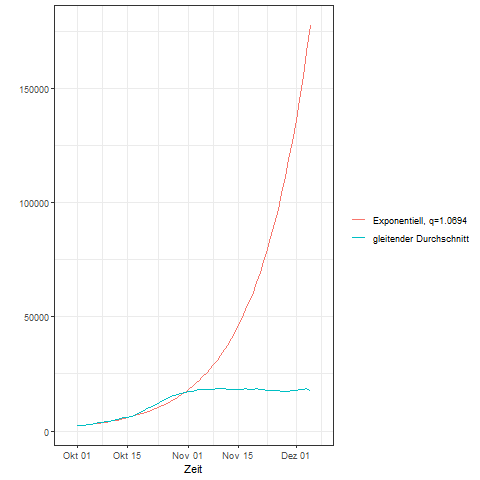
Dem exponentiellen Wachstumsmodell liegt die Annahme einer gleichbleibenden Wachstumsrate zugrunde. Die folgende Animation zeigt für Deutschland die mit einem gleitenden Durchschnitt über 7-Tage geglätteten nachgewiesenen täglichen Covid-19 Neuinfektionen für den Zeitraum vom 28. September bis zum 06. Dezember 2020. Zudem wurde auf Basis der geglätteten Werte für den 01. Oktober und den 29. Oktober ein exponentielles Wachstumsmodell bestimmt. Die Zahl der Neuinfektionen im exponentiellen Wachstumsmodell wurde mit der rot gekennzeichneten Kurve fortgeschrieben und zeigt somit ein unverändertes exponentielles Wachsen der Neuinfektionen über den Zeitpunkt der Lockdown-light Maßnahmen hinaus an.

8.3.1 exponentielles Wachstum in diskreter Zeit

Von einem exponentiellen Wachstum in diskreter Zeit spricht man, wenn die Anzahl der Zuwächse endlich ist.
Die Wachstumsgleichung lautet:

\[x_t=x_0\cdot q^t\] Mit \(q\) wird der gleichbleibende Wachstumsfaktor bezeichnet, so dass für die gleichbleibende Wachstumsrate \(p\) gilt: \[p=q-1\] Der Exponent \(t\) gibt die Anzahl der Zuwächse an. Es wird davon ausgegangen, dass die Zuwächse immer am Ende einer Periode stattfinden.
Mehrjährige Festgeldanlagen mit Zinseszinsen und einem konstanten jährlichen Zinssatz folgen diesem Wachstumsmodell.
Auf Basis einer solchen Geldanlage sollen die folgenden Fragestellungen beantwortet werden.

• In welcher Zeit verdoppelt sich die Geldanlage mit einem Zinssatz in Höhe von \(p\)?

• Wie hoch muss der Zinssatz \(p\) gewählt werden, wenn die Geldanlage in Höhe von \(x_0\) nach \(t\) Jahren \(x_t\) entsprechen soll?

• Welcher Betrag \(x_0\) ist in der Periode \(0\) anzulegen, um nach \(t\) Jahren einen Betrag in Höhe von \(x_t\) ausbezahlt zu bekommen?

Wie ist die Wachstumsgleichung jeweils umzustellen?

Die Antworten finden Sie im folgenden Video:

Bevölkerungswachtum

Viele exponentiell wachsende Größen, wie z.B. die Wohnbevölkerung, wachsen kontinuierlich und nicht nur am Ende einer Zeitperiode. Das Wachstum kann dann am besten durch das exponentielle Wachstumsmodell in stetiger Zeit beschrieben werden. Werden die Wachstumsraten, wie im Folgenden beschrieben, auf Basis der Bevölkerungszahlen aus zwei Zeitpunkten ermittelt und fallen die Wachstumsraten nicht allzu groß aus, so unterscheiden sich die Wachstumsraten des diskreten und des stetigen exponentiellen Wachstumsmodells kaum voneinander.

Im Hinblick auf das exponentielle Wachstumsmodell für die Wohnbevölkerung vereinbaren wir, dass Sie wahlweise das exponentielle Wachstumsmodell in diskreter Zeit oder in stetiger Zeit verwenden dürfen, sofern in der Aufgabenstellung nicht explizit ein bestimmtes der beiden Modelle gefordert wird.

Beispiel

Im Jahr 2008 lebten in Mexiko 111,3 Mio. Menschen. Zur selben Zeit lebten in der Demokratischen Republik Kongo 66,41 Mio. Menschen.
10 Jahre später lebten in Mexiko 124,74 Mio. Menschen und in der DR Kongo 89,25 Mio. Menschen.
Ermitteln Sie auf der Basis des Bevölkerungswachstums in der Dekade 2008-2018 das Jahr, in dem die Bevölkerungszahlen in Mexiko und DR Kongo gleich sein werden.
Die Lösung finden Sie im folgenden Video:

8.3.2 exponentielles Wachstum in stetiger Zeit

Geht man davon aus, dass sich eine Geldanlage unterjährig verzinst und wählt als Ausgangspunkt für die unterjährige Verzinsung die Wachstumsrate \(p\) einer jährlichen Verzinsung, so wird mit \(\frac{p}{n}\) die Wachstumsrate der unterjährigen Verzinsung bezeichnet, wobei mit \(n\) die Frequenz der Verzinsung angegeben wird. Bei monatlicher Verzinsung wäre somit \(n=12\) zu wählen und bei täglicher Verzinsung nach kaufmännischer Rechnung mit 360 Tagen entsprechend \(n=360\).
Der Gesamtwachstumsfaktor bei einer Verzinsung über ein komplettes Jahr ist für beide Varianten in Abbildung 8.3 dargestellt.

8.3: vom diskreten zum stetigen Wachstum

Der Gesamtwachstumsfaktor entspricht im Grenzwert also \(e^p\).
In der Betrachtung über \(t\) Jahre folgt somit für den Gesamtwachstumsfaktor \(\left(e^p\right)^t=e^{p\cdot t}\)

Zur besseren Abgrenzung vom exponentiellen Wachstumsmodell in diskreter Zeit, wird die Wachstumsrate für das Wachstumsmodell in stetiger Zeit nun mit \(b\) bezeichnet.

Grundsätzlich lässt sich im exponentiellen Wachstumsmodell in stetiger Zeit für \(t\) jede beliebige nicht negative reelle Zahl einsetzten.

Das exponentielle Wachstumsmodell in stetiger Zeit lautet dann:

\[x(t)=x(0)\cdot e^{b\cdot t}, \quad t\geq 0\]

Wir beschränken uns in der Anwendung auf eine abzählbare Zahl äquidistanter Zeitreihenwerte für die Modellzeiten \(t=0,...,n\) und notieren daher die Modellgleichung:

\[x_t=x_0\cdot e^{b\cdot t}, \quad t=0,...,n\]

Die Wachstumsrate \(b\) ermitteln wir durch Umstellen bei gegebenen Zeitreihenwerten \(x_0\) und \(x_t\) mit

\[b=\frac{ln(x_t)-ln(x_0)}{t}\]

Beispiel

Betrachtet wird die Zahl der täglich nachgewiesenen Covid-19 Neuinfektionen, welche durch ein exponentielles Wachstumsmodell in stetiger Zeit modelliert werden soll.

• In welcher Zeit verdoppelt sich die Zahl der täglichen Neuinfektionen bei einer Wachstumsrate in Höhe von \(b\)?

• Wie hoch fällt die Wachstumsrate \(b\) aus, wenn sich die Zahl der täglichen Neuinfektionen innerhalb von \(t\) Tagen verdoppelt?

Die beiden Fragen werden im folgenden Video beantwortet:

exponentielle Wachstumsmodelle in diskreter und stetiger Zeit im Vergleich

Wie müsste die Wachstumsrate im Wachstumsmodell in stetiger Zeit gewählt werden, damit in beiden Modellen das Gesamtwachstum über \(t\) Perioden identisch ausfällt?

Zunächst werden die beiden Wachstumsmodelle gleichgesetzt, da diese jeweils nach \(t\) Perioden einen identischen Wert \(x_t\) erzielen sollen:

\[\begin{align} x_0 \cdot q^t&\overset{!}{=}x_0\cdot e^{b\cdot t}\\ \Leftrightarrow \quad q^t&=e^{b\cdot t}\\ \Leftrightarrow \quad \ b&=ln(q)=ln(1+p) \end{align}\]

Nur für kleine Wachstumsraten liegen die diskrete Wachstumsrate \(p\) und die stetige Wachstumsrate \(b\) nahe beieinander.

Beispiel:

\[p=0,03 \Rightarrow b=ln(1,03)=0,02956\thickapprox 0,03\] hingegen \[p=0,5 \Rightarrow b=ln(1,5)=0,405465\neq 0,5\]

Die folgende Grafik zeigt auf, wie die Wachstumsraten \(p\) und \(b\) gewählt werden müssten, um in den Wachstumsmodellen in diskreter und stetiger Zeit ein identisches Wachstum zu erzielen.

Zurückblickend lässt sich an dieser Stelle noch festhalten, dass man durch Anwendung des exponentiellen Wachstumsmodells in stetiger Zeit auf die Fragestellung des Bevölkerungsgleichstands der Länder Mexiko und DR Kongo zum selben Ergebnis gekommen wäre, wie durch Anwendung des exponentiellen Wachstumsmodells in stetiger Zeit.

Wie oben gesehen, unterscheiden sich die Modelle nur in der Schreibweise der Faktoren \(q=\left(\frac{x_t}{x_0}\right)^\frac{1}{t}\) und \(e^b\), welche bei gegebenen Zeitreihenwerten \(x_t\) und \(x_0\) identisch sein müssen.

Dies lässt sich auch erkennen, wenn wir für die stetige Wachstumsrate \(b\) die Berechnungsvorschrift \(b=\frac{ln(x_t)-ln(x_0)}{t}\) einsetzen:

\[e^b=e^{\frac{ln(x_t)-ln(x_0)}{t}}=e^{\frac{1}{t}\cdot{ln\left(\frac{x_t}{x_0}\right)}}=e^{{ln\left(\left(\frac{x_t}{x_0}\right)^\frac{1}{t}\right)}}=\left(\frac{x_t}{x_0}\right)^\frac{1}{t}=q\]