Kapitel 11 axiomatische Wahrscheinlichkeitsrechnung

Auch die axiomatische Wahrscheinlichkeitsrechnung fußt auf Mengen möglicher und günstiger Resultate von Zufallsvorgängen.
Die folgenden Bezeichnungen werden verwendet:

\(\Omega=\{\omega_1,\omega_2,...\}\) steht für die Menge aller möglichen Resultate, welche auch als Elementarereignisse bezeichnet werden.
Ereignisse werden mit \(A_i\) bezeichnet und stellen jeweils Teilmengen von \(\Omega\) dar. Im Folgenden wird mit \(A_i\) der Einfachheit halber dann auch direkt die Menge der zugehörigen Resultate (Elementarereignisse) bezeichnet.

Beispiel: Für einen fairen Würfel mit den Ereignissen \(A_1:=\mbox{gerade Augenzahl}\) und \(A_2:=\mbox{keine Fünf}\) gilt:

\(\Omega=\{1,2,3,4,5,6\}\)
\(A_1=\{2,4,6\}\)
\(A_2=\{1,2,3,4,6\}\)

11.1 Voraussetzungen aus der Mengenlehre

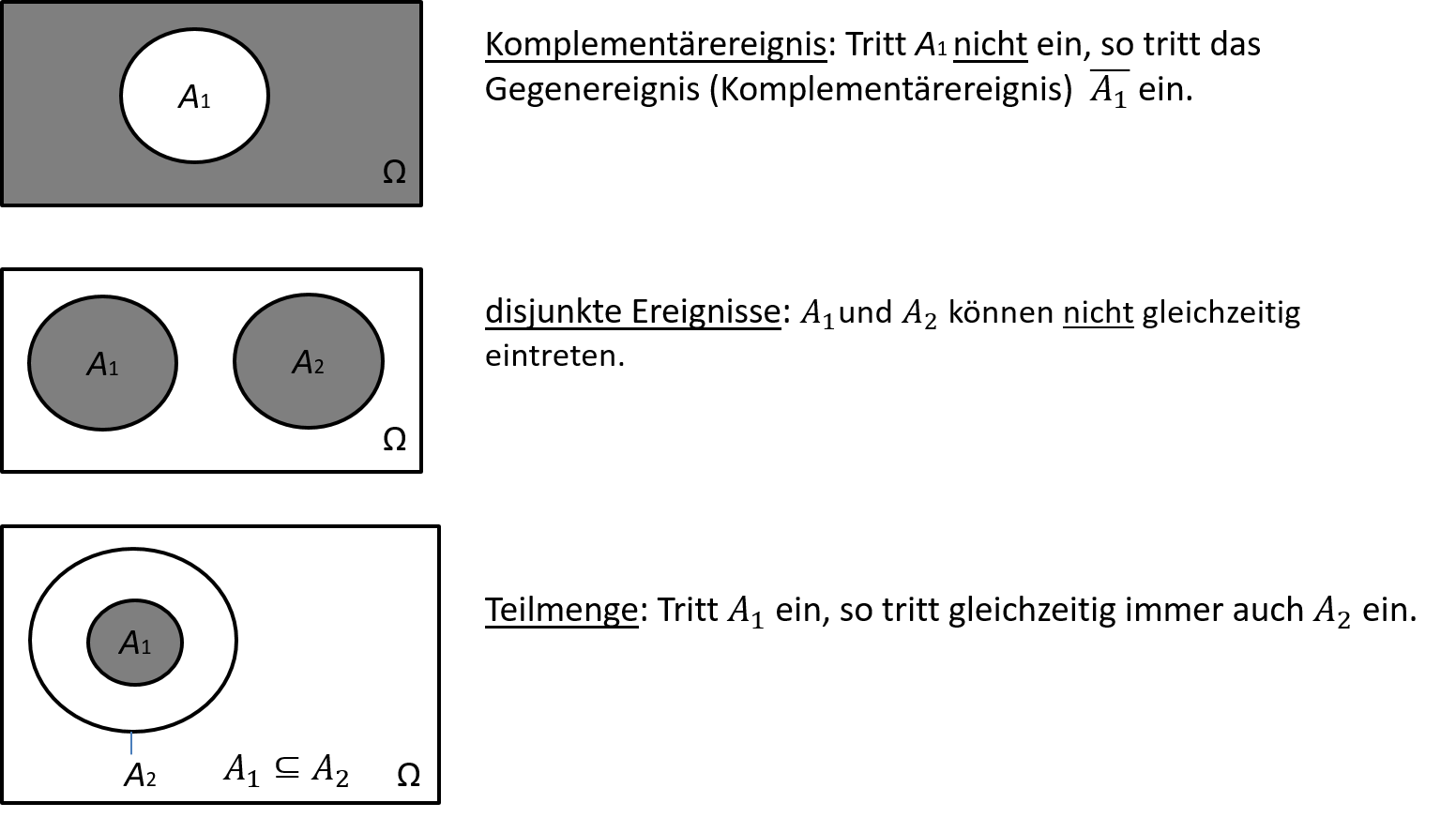
Abbildung 11.1 zeigt drei Mengendiagramme (Venn-Diagramme). Das Rechteck symbolisiert jeweils die Menge aller möglichen Resultate \(\Omega\) des Zufallsvorgangs. Mit \(A_1\) bzw. \(A_2\) werden Ereignisse, also Teilmengen von \(\Omega\), bezeichnet. Grau hinterlegt sind jeweils jene Ereignisse, welche gerade im Fokus stehen.

Die obere Abbildung zeigt mit \(\overline{A}_1\) das Gegenereignis (Komplementärereignis) zu \(A_1\). Das Gegenereignis zu \(A_1=\{2,4,6\}\) lautet beim Würfelwurf: \(\overline{A}_1=\{1,3,5\}\).
Die mittlere Abbildung zeigt zwei disjunkte Ereignisse (Ereignisse ohne Schnittmenge) \(A_1\) und \(A_2\), welche aufgrund der nicht vorhandenen Schnittmenge nicht gleichzeitig eintreten können. Ein Ereignis und das zugehörige Gegenereignis sind immer disjunkt. Beim Würfelwurf ist die Augenzahl also entweder gerade (\(A_1\)) oder ungerade (\(\overline{A}_1\)).
Die untere Abbildung zeigt das Ereignis \(A_1\) als Teilmenge von \(A_2\), geschrieben als \(A_1 \subseteq A_2\). Da also \(A_1\) vollständig in \(A_2\) enthalten ist, tritt \(A_2\) immer ein, wenn \(A_1\) eintritt. Das Ereignis \(A_1\) aus dem Beispiel ist Teilmenge des Ereignis \(A_2=\{1,2,3,4,6\}\).

11.1: Exkurs Mengenlehre 1

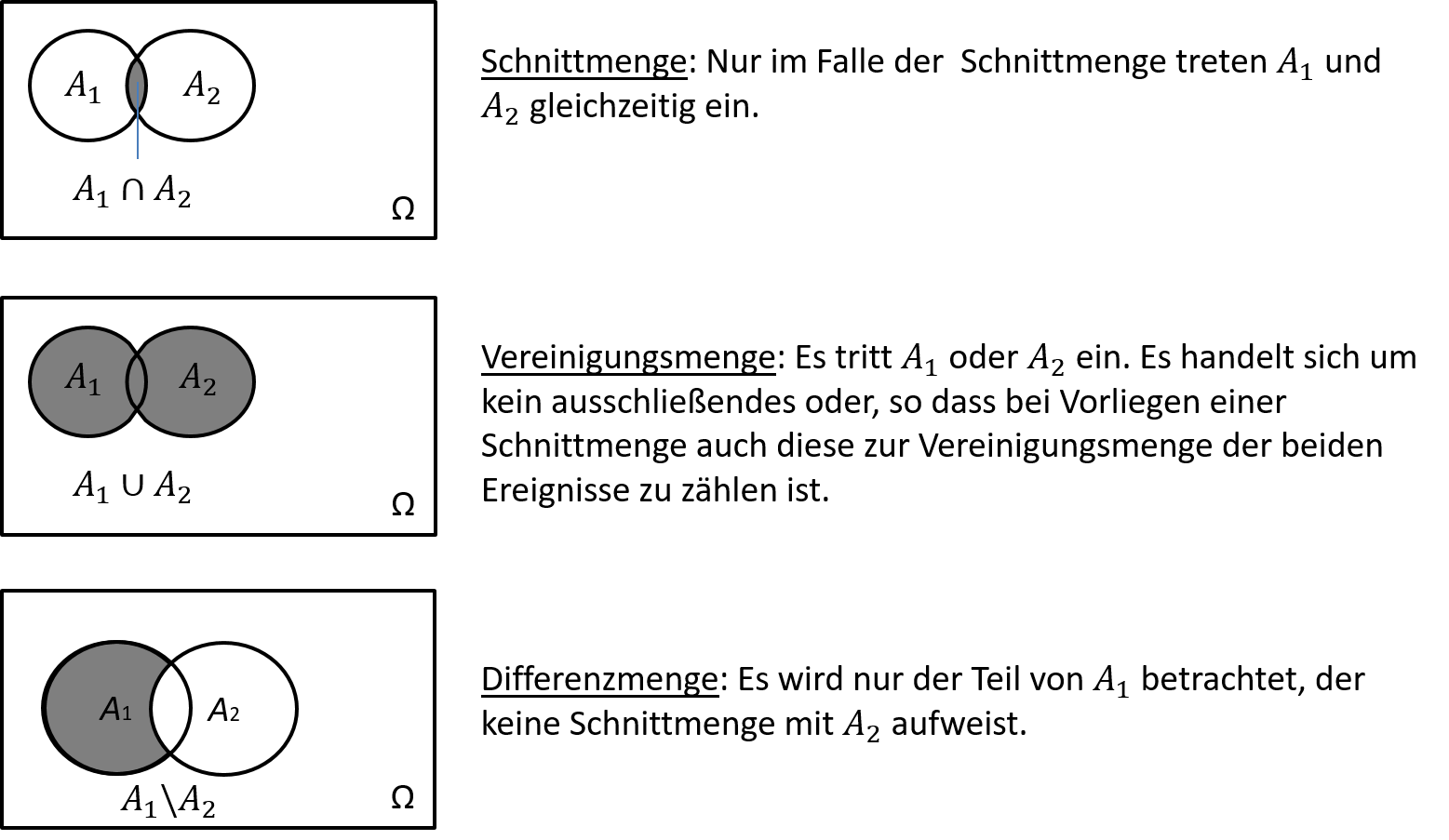
Drei weitere Mengendiagramme sind in Abbildung 11.2 zu sehen.

Die obere Abbildung zeigt mit \(A_1 \cap A_2\) die Schnittmenge der Ereignisse \(A_1\) und \(A_2\). Beim Eintreten von Resultaten aus der Schnittmenge treten also immer sogleich \(A_1\) und \(A_2\) ein. Für die Ereignisse \(\overline{A}_1=\{1,3,5\}\) und \(A_2=\{1,2,3,4,6\}\) ist \(\overline{A}_1\cap A_2=\{1,3\}\).
Die mittlere Abbildung zeigt mit \(A_1 \cup A_2\) die Vereinigungsmenge der Ereignisse \(A_1\) und \(A_2\). Es tritt also \(A_1\) oder \(A_2\) ein, falls Resultate aus der Vereinigungsmenge eintreten. Die Schnittmenge von \(A_1\) und \(A_2\) ist immer auch Bestandteil der Vereinigungsmenge \(A_1 \cup A_2\). Im Beispiel gilt also: \(\overline{A}_1\cup A_2=\{1,2,3,4,5,6\}=\Omega\)
Die untere Abbildung zeigt die Differenzmenge \(A_1 \backslash A_2\). Diese umfasst nur jene Resultate aus \(A_1\), welche nicht zur Schnittmenge mit \(A_2\) zählen. Im Beispiel ist \(\overline{A}_1 \backslash A_2=\{5\}\). Die Differenzmenge zweier Ereignisse \(A_1\) und \(A_2\) kann allgemein auch durch Schnittbildung und die Betrachtung von Gegenereignissen erzeugt werden: \(A_1 \backslash A_2=A_1\cap\overline{A}_2\)

11.2: Exkurs Mengenlehre 1

De Morgansche Gesetze

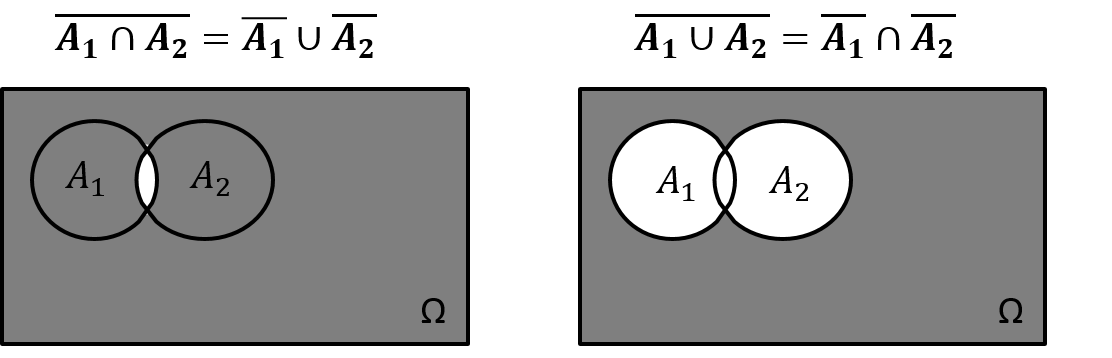
Abbildung 11.3 veranschaulicht die nach dem Mathematiker Augustus De Morgan benannten Gesetze.

Die linke Abbildung zeigt, wie das Gegenereignis aus dem Schnitt von \(A_1\) und \(A_2\) auch durch Vereinigung der beiden Gegenereignisse zu \(A_1\) und \(A_2\) erzeugt werden kann: \[\overline{A_1\cap A_2}=\overline{A_1} \cup \overline{A_2}\] Im Beispiel gilt: \(\overline{A_1\cap A_2}=\overline{A_1} \cup \overline{A_2}=\{1,3,5\}\)

Die rechte Abbildung zeigt, wie das Gegenereignis zu der Vereinigung aus \(A_1\) und \(A_2\) auch durch Schnittbildung der Gegenereignisse zu \(A_1\) und \(A_2\) erreicht werden kann: \[\overline{A_1 \cup A_2}=\overline{A}_1 \cap \overline{A}_2\] Im Beispiel gilt: \(\overline{A_1 \cup A_2}=\overline{A}_1 \cap \overline{A}_2=\{5\}\)

11.3: Gesetze von De Morgan

Mit den Gesetzen von De Morgan lässt sich zeigen, dass die Schnittmenge von zwei Ereignissen, also \(A_1 \cap A_2\) durch die Betrachtung von Gegenereignissen und der Erzeugung von Vereinigungsmengen erreicht werden kann, denn greift man auf das erstgenannte Gesetz zurück und betrachtet das Gegenereignis, so erhält man: \[A_1 \cap A_2=\overline{\overline{A}_1\cup \overline{A}_2}\]

Auch für die Betrachtung von mehr als zwei Ereignissen gilt, dass sich alle möglichen Schnittmengen aus den Ereignissen durch Vereinigung und Betrachtung von Gegenereignissen (Komplementärereignissen) bilden lassen. Diese Erkenntnis spielt im Folgenden noch eine wichtige Rolle für den axiomatischen Ansatz der Wahrscheinlichkeitsrechnung.

11.2 Der axiomatische Ansatz der Wahrscheinlichkeitstheorie

Bei genauerer Betrachtung des klassischen Wahrscheinlichkeitsbegriffs wird deutlich, dass lediglich eine endliche Anzahl von Resultaten unter der Gleichwahrscheinlichkeitsprämisse zugrunde gelegt ist.
Der russische Mathematiker Andrey Nikolaevich Kolmogorov veröffentlichte 1933 einen allgemeineren Wahrscheinlichkeitsbegriff, welcher auch die klassische Definition beinhaltet, aber nicht den genannten Einschränkungen unterliegt. Zu diesem Zweck formulierte er bestimmte mathematische Minimalanforderungen (Axiome) an ein Wahrscheinlichkeitsmaß.

11.2.1 \(\sigma\)-Algebra

Den Ausgangspunkt bildet ein Mengensystem \(S\) welches als \(\sigma\)-Algebra bezeichnet wird. Es gilt:

\(\Omega \in S\). \(\Omega\) ist nicht leer und stellt die Menge aller möglichen Resultate des Zufallsvorgangs dar und ist als sicheres Ereignis in \(S\) enthalten. Darüber hinaus können noch weitere Ereignisse in \(S\) enthalten sein, welche jeweils Teilmengen von \(\Omega\) sind. Diese werden mit Großbuchtaben bezeichnet.
\(\overline{A} \in S\), falls \(A \in S\) Für jedes in \(S\) enthaltene Ereignis ist also auch dessen Gegenereignis in \(S\) enthalten.
\(\cup_i A_i \in S\), für alle \(A_i \in S\). Sämtliche Vereinigungen, welche aus den in \(S\) enthaltenen Ereignissen gebildet werden können, gehören zu \(S\). Es ist festzuhalten, dass das Mengensystem \(S\) somit abgeschlossen in Bezug auf die Bildung von Vereinigungsmengen und die Bildung von Gegenereignissen ist.

Folgerungen:

\(\cap_i A_i \in S\), für alle \(A_i \in S\). Sämtliche Schnittmengen, welche aus den in \(S\) enthaltenen Ereignissen gebildet werden können, sind durch die Bildung von Vereinigungen und Gegenereignissen bereits in \(S\) enthalten.
Neben dem sicheren Ereignis \(\Omega\) gehört als dessen Gegenereignis auch das unmögliche Ereignis \(\emptyset\) zu \(S\).

Im folgenden Video wird die \(\sigma\)-Algebra \(S\) für das vorangegangene Beispiel des Würfelwurfs mit den Ereignisse \(A_1=\{2,4,6\}\) und \(A_2=\{1,2,3,4,6\}\) bestimmt:

11.2.2 Wahrscheinlichkeitsfunktion

Eine Funktion \(W\), welche den Ereignissen aus \(S\) Wahrscheinlichkeiten in Form von reellen Zahlen zuordnet, also \[W: S \rightarrow \mathbb{R}\] heißt Wahrscheinlichkeitsfunktion, sofern die folgenden drei Axiome erfüllt sind:

\(W(A)\geq 0\), für jedes \(A \in S\)
Die Wahrscheinlichkeiten sind somit nicht negativ.
\(W(\cup_i A_i)=\sum_i W(A_i)\), für \(A_i \in S,\) welche paarweise disjunkt sind
Die in diesem Axiom geforderte Eigenschaft wird als Totaladditivität bezeichnet.
\(W(\Omega)=1\)
Die Wahrscheinlichkeit für das sichere Ereignis wird somit auf 1 normiert.

Die Zusammenstellung aus\((\Omega, S, W)\) wird als Wahrscheinlichkeitsraum bezeichnet.

11.2.3 Folgerungen aus den Axiomen

Die nachfolgend genannten Folgerungen aus Axiomen erleichtern in bestimmten Fällen das Rechnen mit Wahrscheinlichkeiten und können für Beweise herangezogen werden:

\(W(\overline{A})=1-W(A)\)
\(W(\emptyset)=0\)
\(W(A_1) \leq W(A_2) \mbox{ für } A_1\subseteq A_2\)
\(W(A)\leq 1\)
\(W(A \cup B)=W(A)+W(B)-W(A \cap B)\)
\(W(A)=\sum_i W(A \cap B_i)\), falls \(\{B_1,B_2,...\}\) eine Zerlegung von \(\Omega\) ist, mit \(B_i \in S\)
\(\{B_1,B_2,...\}\) ist eine Zerlegung von \(\Omega\), falls
1. die Menge \(\{B_1,B_2,...\}\) abzählbar ist,
2. die in der Menge enthaltenen Ereignisse \(B_i\) paarweise disjunkt sind,
3. \(\Omega=B_1\cup B_2\cup ...\)

Die Herleitungen der Folgerungen sollen hier nicht näher betrachtet werden. Als Beispiel für eine Zerlegung kann ein Würfel mit den Ereignissen “\(B_1:=\)gerade Zahlen” und “\(B_2:=\)ungerade Zahlen” betrachtet werden. Die Ereignisse \(B_1\) und \(B_2\) sind dann disjunkt, also \(B_1\cap B_2=\emptyset\) und für deren Vereinigung gilt: \(\underbrace{B_1}_{\{2,4,6\}}\cup \underbrace{B_2}_{\{1,3,5\}}=\underbrace{\Omega}_{\{1,2,3,4,5,6\}}\)

11.3 stochastische Unabhängigkeit

Werden im Rahmen eines Zufallsvorgangs zwei oder mehr Ereignisse zugleich betrachtet, so interessiert man sich dafür, ob zwischen dem Eintreten dieser Ereignisse Zusammenhänge existieren oder nicht. Falls ein Zusammenhang existiert, kann z.B. nach einem kausalen Zusammenhang zwischen beiden Ereignissen gesucht werden (Ökonomische Theorie, z.B. ,,Wenn das Einkommen steigt, steigt - als Folge daraus - auch der Konsum.”). Für stochastische Betrachtungen (also der Betrachtung von Zufallsvorgängen) spielt der Begriff der stochastischen Unabhängigkeit (kurz Unabhängigkeit) eine wichtige Rolle.

11.3.1 Unabhängigkeit von zwei Ereignissen

Betrachtet werde ein Wahrscheinlichkeitsraum \((\Omega, S, W)\).
Zwei Ereignisse \(A\) und \(B\) heißen genau dann unabhängig, falls \[W(A\cap B)=W(A)\cdot W(B)\] Sind zwei Ereignisse \(A\) und \(B\) unabhängig, so sind auch die folgenden Ereignisse voneinander unabhängig:

\(A\) und \(\overline{B}\)
\(\overline{A}\) und \(B\)
\(\overline{A}\) und \(\overline{B}\)

Im folgenden Video wird gezeigt, dass die Ereignisse \(\overline{A}\) und \(B\) unabhängig sind, falls die Ereignisse \(A\) und \(B\) unabhängig sind. Genauso kann gezeigt werden, dass dann auch die Ereignisse \(A\) und \(\overline{B}\) unabhängig sind, als auch die Ereignisse \(\overline{A}\) und \(\overline{B}\) unabhängig sind.

Im Rahmen der folgenden Beispielaufgabe zur Unabhängigkeit von zwei Ereignissen wird für deren Lösung auf Folgerungen aus den Axiomen zurückgegriffen:

11.3.2 gemeinsame Unabhängigkeit

Bei mehr als zwei Ereignissen wird zwischen paarweiser Unabhängigkeit und gemeinsamer (en bloc) Unabhängigkeit unterschieden.
Ausgangspunkt sei ein Wahrscheinlichkeitsraum \((\Omega, S, W)\) mit \(A_1,...,A_n \in S\).
Die \(n\) Ereignisse heißen genau dann paarweise unabhängig, wenn \[W(A_i\cap A_j)=W(A_i)\cdot W(A_j) \ \ \mbox{für alle} \ \ i \neq j\] Die Ereignisse \(A_1,A_2,...,A_n\) heißen genau dann gemeinsam unabhängig, falls für alle \(\sum_{k=2}^n \binom{n}{k}\) unterschiedlichen Teilauswahlen von Ereignissen aus der Gesamtheit aller Ereignisse, also \[\{A_{i_1},A_{i_2},...,A_{i_m} \}\subseteq \{A_1,A_2,...,A_n\}\] gilt: \[ W(A_{i_1}\cap A_{i_2}\cap...\cap A_{i_m})=W(A_{i_1})\cdot W(A_{i_2})\cdot...\cdot W(A_{i_m}) \] Folglich sind gemeinsam unabhängige Ereignisse dann auch paarweise unabhängig, wegen der bereits berücksichtigten Teilauswahlen. \[\{A_{i_1}, A_{i_2}\} \subseteq \{A_1,A_2,...,A_n\}\] Aus der paarweisen Unabhängigkeit kann jedoch nicht die gemeinsame Unabhängigkeit gefolgert werden.
Beispiel:
Die drei Ereignisse \(A_1, A_2, A_3\) sind also dann gemeinsam unabhängig, falls gilt:

\[\begin{align} W(A_1\cap A_2)&=W(A_1)\cdot W(A_2)\\ W(A_1\cap A_3)&=W(A_1)\cdot W(A_3)\\ W(A_2\cap A_3)&=W(A_2)\cdot W(A_3)\\ &\\ W(A_1\cap A_2 \cap A_3)&=W(A_1)\cdot W(A_2) \cdot W(A_3) \end{align}\]

Falls nur die ersten drei Gleichungen erfüllt sind, so sind die Ereignisse paarweise unabhängig. Wenn alle vier Gleichungen erfüllt sind, so sind die Ereignisse gemeinsam unabhängig.
Im folgenden Video wird ein Beispiel für paarweise unabhängige Ereignisse aufgezeigt, welche aber nicht gemeinsam unabhängig sind:

11.3.3 kurze Aufgaben zur paarweisen und gemeinsamen Unabhängigkeit

Würfelaufgabe

Von den sechs Seiten eines Würfels ist eine Seite blau, eine Seite gelb und eine Seite rot gefärbt. Die übrigen drei Seiten sind mit allen drei Farben (blau, gelb und rot) gefärbt.

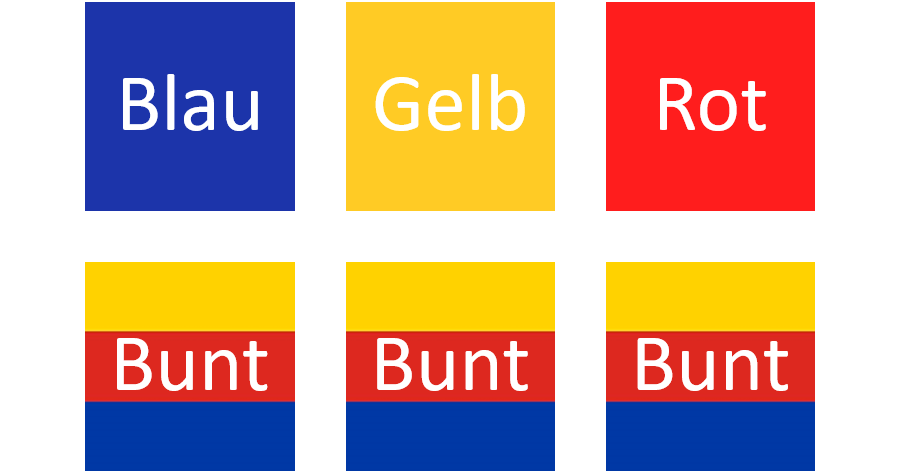
11.4: gefärbter Würfel

Die folgenden Ereignisse werden betrachtet:
A: Es wird eine Seite gewürfelt, welche blaue Farbe aufweist.
B: Es wird eine Seite gewürfelt, welche gelbe Farbe aufweist.
C: Es wird eine Seite gewürfelt, welche rote Farbe aufweist.

Tetraederaufgabe

Gehen wir nun davon aus, dass es sich um einen Tetraeder (4 Seiten) handelt, welcher gewürfelt werden soll. Eine Seite ist blau, eine Seite ist gelb, eine Seite ist rot und die vierte Seite ist mit allen drei Farben (blau, gelb und rot) gefärbt worden. Der aufgefaltete Tetraeder wird in der nachfolgenden Abbildung dargestellt:

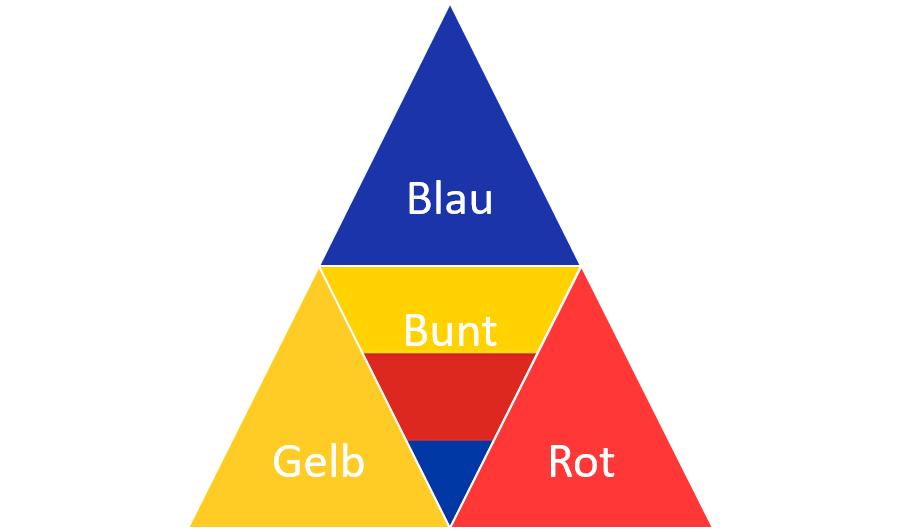
11.5: gefärbter Tetraeder

Betrachtet werden weiterhin die Ereignisse A, B und C.
zur Erinnerung:
A: Es wird eine Seite gewürfelt, welche blaue Farbe aufweist.
B: Es wird eine Seite gewürfelt, welche gelbe Farbe aufweist.
C: Es wird eine Seite gewürfelt, welche rote Farbe aufweist.