Kapitel 2 Datenlagen und graphische Darstellungen

Daten können auf unterschiedliche Weisen präsentiert werden. Unterschieden werden drei sogenannte Datenlagen.
Im folgenden Video wird ein einführender Überblick über die drei Datenlagen gegeben:

2.1 Datenlage A

Die Datenlage A, auch Urliste genannt, entspricht der Auflistung aller Beobachtungen zur Grundgesamtheit. Die \(n\) Merkmalsträger der Grundgesamtheit werden mit den natürlichen Zahlen von \(1\) bis \(n\) durchnummeriert. Die Beobachtungen werden mit der Variablen \(x_i\) bezeichnet, wobei der Index \(i\) die Zuordnung zum jeweiligen Merkmalsträger vornimmt. Die (unsortierte) Urliste lautet also \[x_1,x_2,...,x_n\] Im folgenden Beispiel betrachten wir für 10 Studierende die benötigten Fachsemester bis zum Bachelorabschluss. Studentin 1 benötigte also 7 Fachsemester bis zum Abschluss, Student 2 benötigte 6 Fachsemester usw.

\(i\)	1	2	3	4	5	6	7	8	9	10
\(x_i\)	7	6	5	7	7	6	9	8	7	8

Bei quantitativen Merkmalen können die Werte der Urliste entsprechend der Ordnung der reellen Zahlen, bei ordinal skalierten Merkmalen gemäß der Ordnungsrelation sortiert werden. Man erhält dann die geordnete Urliste \[x_{(1)}\leq x_{(2)}\leq...\leq x_{(n)}\] Der Indexwert in der runden Klammer steht für die Position in der geordneten Urliste. Für das Beispiel folgt:

\((i)\)	1	2	3	4	5	6	7	8	9	10
\(x_{(i)}\)	5	6	6	7	7	7	7	8	8	9

2.2 Datenlage B

2.2.1 Häufigkeitstabelle

Liegen viele Beobachtungen vor, so sind Urlisten zur Präsentation des Datensatzes sehr unübersichtlich. Sofern es viele identische Beobachtungswerte im Datensatz gibt, was häufig bei diskreten Merkmalen der Fall ist, verschaffen Häufigkeitstabellen ohne Informationseinbußen einen guten Überblick über die Daten. Es wird im Folgenden ein Beispiel mit wesentlich mehr Beobachtungen \((n=80)\) als im vorherigen Beispiel betrachtet:

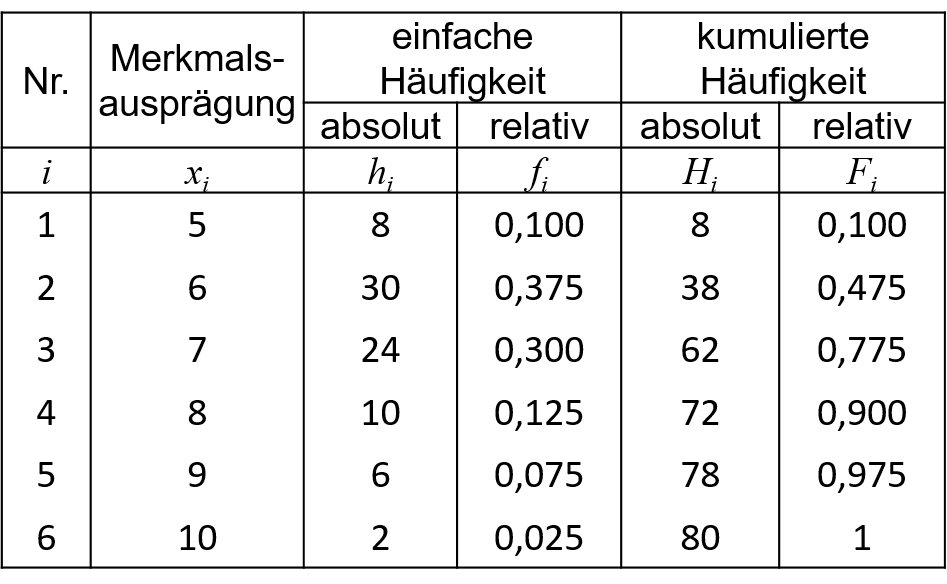
2.1: Datenlage B, Fachsemester

Es wurden die folgenden Variablen verwendet:

\(n\) steht für die Anzahl der Beobachtungen.
\(m\) steht für die Anzahl der voneinander verschiedenen Merkmalsausprägungen, für die Beobachtungen vorliegen. Im Beispiel ist also \(m=6\).
Mit \(x_i\) werden jene Merkmalsausprägungen bezeichnet, für die Beobachtungswerte vorliegen.
Zu jedem \(x_i\) wird die absolute Häufigkeit mit \(h_i\) angegeben.
\(f_i\) sind die relativen Häufigkeiten, für die gilt: \(f_i=\frac{h_i}{n}\)

Ab Ordinalskalenniveau können, wie im Beispiel, kumulierte Häufigkeiten angegeben werden.

\(H_i=\sum_{j=1}^i h_j\) sind die kumulierten absoluten Häufigkeiten.
\(F_i=\sum_{j=1}^i f_j=\frac{H_i}{n}\) sind die kumulierten relativen Häufigkeiten.

Videoclip zur Notation der kumulierten Häufigkeiten mit Hilfe des Summenzeichens

Betrachtet man beispielsweise in Tabelle 2.1 mit \(i=3\) die Zeile zur dritten Ausprägung mit \(x_3=7\), so ist festzuhalten, dass mit \(h_3=24\), also 24 Absolventinnen und Absolventen 7 Fachsemester bis zum Abschluss benötigt haben. Ferner mach das einen Anteil von genau 30% (\(f_3=0.3\)) an der Gesamtzahl der Absolventinnen und Absolventen aus. Aus den kumulierten Häufigkeiten geht hervor, dass 62 Absolventinnen und Absolventen höchsten 7 Fachsemester benötigt haben (\(H_3=62\)), was einem Anteil von 77,5% entspricht (\(F_3=0,775\)).

2.2.2 Stabdiagramm

Zur Veranschaulichung der Häufigkeitsverteilung können Stabdiagramme verwendet werden. Die Stablängen müssen sich dabei proportional zu den einfachen Häufigkeiten verhalten. Es können wahlweise die absoluten oder die relativen Häufigkeiten Anwendung finden.

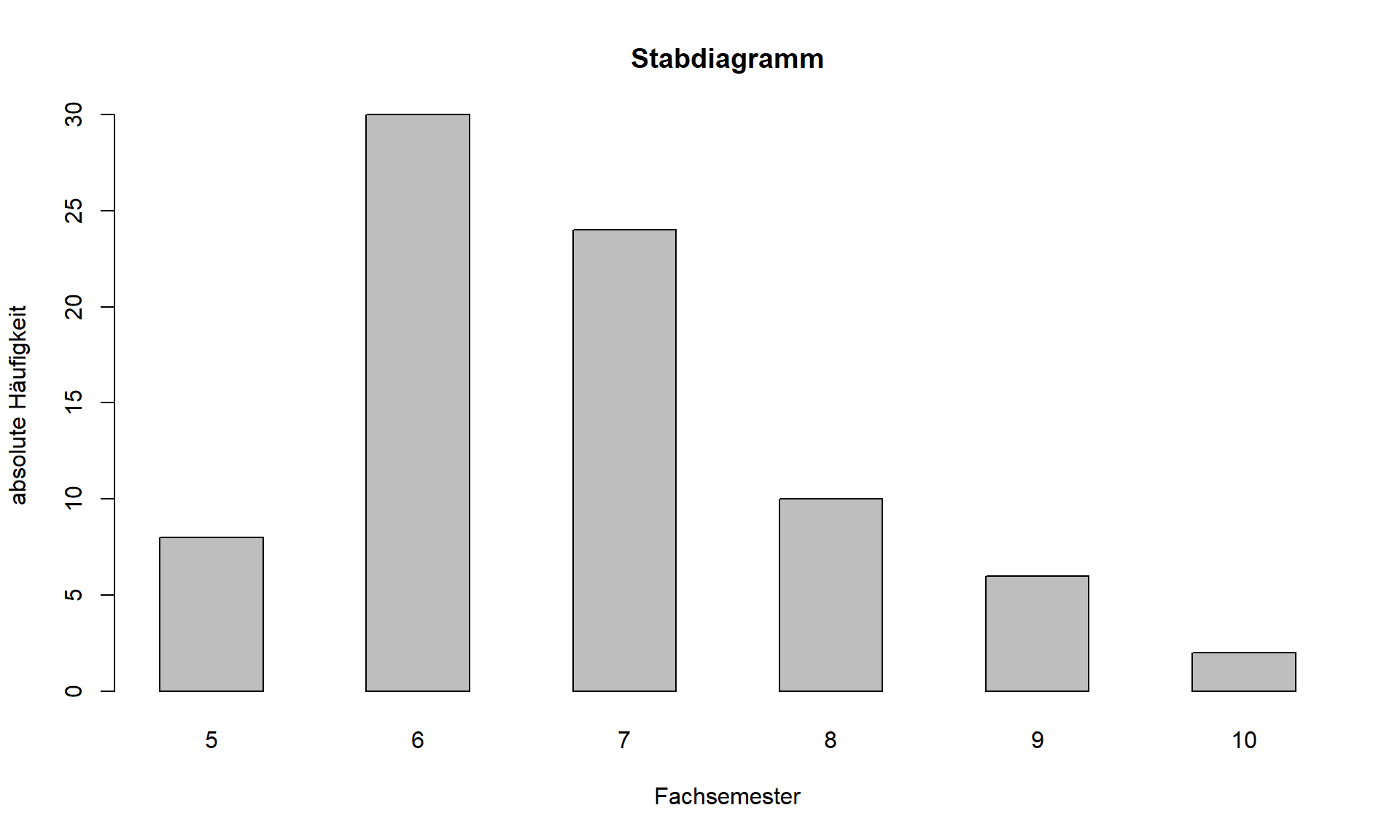
2.2: Stabdiagramm Merkmal Fachsemester

Stabdiagramme können bereits für nominalskalierte Daten verwendet werden. Ab Ordinalskalenniveau müssen die Ausprägungen auf der Abszisse (X-Achse) entsprechend ihrer natürlichen Reihenfolge angeordnet werden. Für quantitative Merkmale gilt, dass die Abstände auf der Abszisse entsprechend ihrer Ausprägungen auf der Skala zu wählen sind.

2.2.3 empirische Verteilungsfunktion

Die empirische Verteilungsfunktion \(F(x)\) kann ab Intervallskalenniveau bestimmt werden und zeigt für jede reelle Zahl \(x\) den relativen Anteil der Beobachtungen an, die kleiner oder gleich dem Wert \(x\) sind. Die kumulierten relativen Häufigkeiten \(F_i=F(x_i)\) liefern alle benötigten Informationen.

Definition empirische Verteilungsfunktion:

\[F(x) = \begin{cases} 0 & \mbox{für} \ \ x < x_1 \\ F_{i} &\mbox{für} \ \ x_{i}\leq x < x_{i+1}, \ \ \mbox{mit} \ \ i \in \{1,...,m-1\} \\ 1 &\mbox{für} \ \ x_m\leq x \end{cases}\]

Die empirische Verteilungsfunktion besitzt die folgenden Eigenschaften:

Die Funktion \(F(x)\) ist rechtsseitig stetig.

D.h. \(\underset{c \rightarrow 0}{\lim} F(x+c)=F(x), \ c \in \mathbb{R}^+\)
und an den Sprungstellen \(x=x_i\) gilt: \(\underset{c \rightarrow 0}{\lim} F(x+c) \neq F(x), \ c \in \mathbb{R}^-\)
\(F(x)\) ist monoton steigend.

D.h. \(F(a)\leq F(b) \ \mbox{für} \ a<b, \ \mbox{mit} \ a,b \in \mathbb{R}\)
Die Grenzwerte von \(F(x)\) sind 0 (untererer Grenzwert) und 1 (oberer Grenzwert).

D.h. \(0 \leq F(x) \leq 1\) mit \(\underset{x \rightarrow -\infty}{\lim} F(x)=0\) und \(\underset{x \rightarrow \infty}{\lim} F(x)=1\)

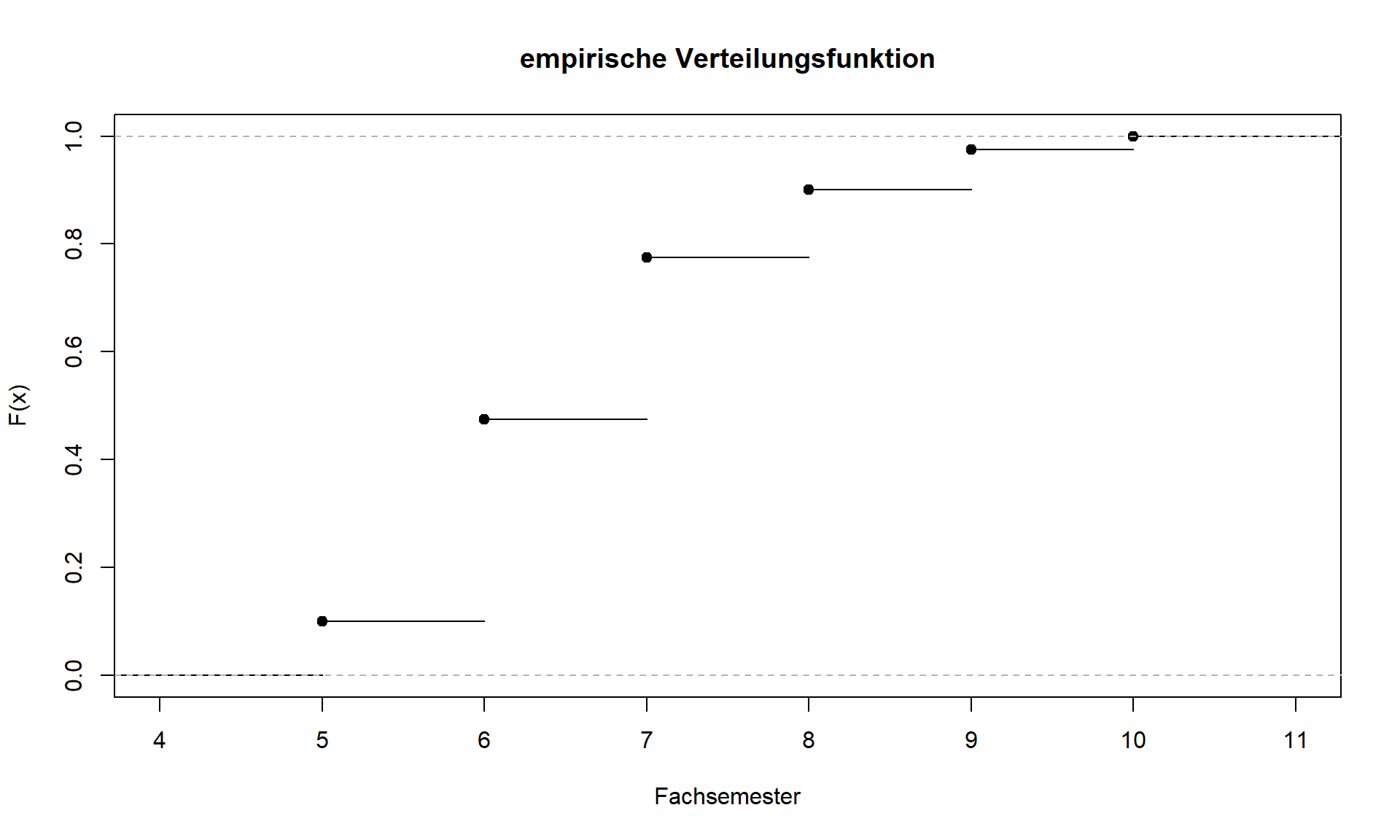
2.3: Verteilungsfunktion Merkmal Fachsemester

2.3 Datenlage C

2.3.1 Häufigkeitstabelle

Liegen sehr viele voneinander verschiedene Beobachtungen vor, so wird die Häufigkeitstabelle für die Datenlage B sehr unübersichtlich. Im Extremfall gibt es, typisch für stetige Merkmale, ausschließlich voneinander verschiedene Beobachtungswerte. Somit würde die Datenlage B praktisch der Datenlage A gleichen, ergänzt um unnötige Häufigkeitsangaben. In diesen Fällen ist es sinnvoll Klassen zu bilden. Sinnvoll ist die Klassenbildung in der Regel erst ab Intervallskalenniveau. Im Beispiel aus Tabelle 2.4 wird für 80 Bachelorabsolventinnen und -absolventen das monatliche Bruttoeinkommen in € betrachtet.

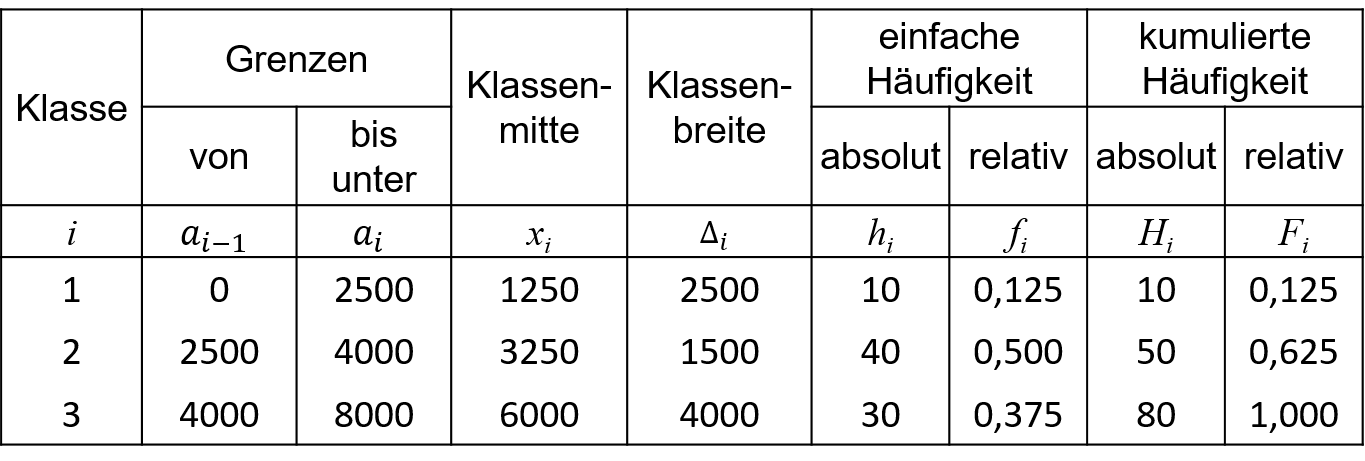
2.4: Datenlage C, monatl. Einkommen in Tsd. €

Es wurden die folgenden Variablen verwendet:

\(n\) steht für die Anzahl der Beobachtungen.
\(k\) steht für die Anzahl der Klassen.
\(a_{i-1}\) steht für die Untergrenze der Klasse \(i\). Beobachtungen, die mit \(a_{i-1}\) übereinstimmen fallen in die Klasse \(i\).
\(a_{i}\) steht für die Obergrenze der Klasse \(i\). Beobachtungen, die mit \(a_{i}\) übereinstimmen fallen in die Folgeklasse \(i+1\). Die Klasse \(i\) reicht von \(a_{i-1}\) bis unter \(a_i\) entspricht der Intervallschreibweise \([a_{i-1},a_i)\), welche alternativ verwendet werden kann.
\(x_i=\frac{a_{i-1}+a_i}{2}\) bezeichnet die Klassenmitte der Klasse \(i\).
Die einfachen und gemeinsamen Häufigkeiten werden analog zur Datenlage B mit \(h_i\), \(f_i\), \(H_i\) und \(F_i\) bezeichnet.

Betrachtet man beispielsweise mit \(i=2\) die Klasse 2, so ist zu erkennen, dass die Klasse von einem Einkommen von 2500€ (\(a_1=2500\)) bis unter 4000€ (\(a_2=4000\)) reicht. Die Klassenmitte liegt bei 3250€ (\(x_2=\frac{2500+4000}{2}=3250\)) und die Klassenbreite liegt bei 1500€ (\(\Delta_2=4000-2500=1500\)). Insgesamt haben 40 Absolventinnen und Absolventen (\(h_2=40\)) Einkommen, welche in Klasse 2 fallen. Dies entspricht einem Anteil von 50% an der Gesamtzahl der Absolventinnen und Absolventen (\(f_2=0.5\)). Einkommen bis unter 4000€ weisen 50 Absolventinnen und Absolventen auf (\(H_2=50\)), was einem Anteil von 62,5% entspricht (\(F_2=0,625\)).

Durch die Klassenbildung kann ein Datensatz wesentlich übersichtlicher präsentiert werden, jedoch geht dies mit einem Informationsverlust einher, denn aus der Datenlage C ist nicht mehr ersichtlich, welche Beobachtungswerte überhaupt zugrunde liegen. Je weniger Klassen gebildet werden, umso gravierender fällt der Informationsverlust aus. Sehr viele Klassen lassen die Daten jedoch unübersichtlich erscheinen, weshalb ein geeigneter Kompromiss aus Informationsverlust und Gewinn an Übersichtlichkeit zu wählen ist. Weitere Schwierigkeiten können im Hinblick auf die Auswertung der Daten entstehen, wenn offene Randklassen existieren. So kann z.B. beim Fehlen einer Klassenobergrenze für die letzte Klasse die Klassenmitte nur durch zusätzliche Informationen oder das Treffen von Annahmen angegeben werden.

2.3.2 Histogramm

Zur Veranschaulichung der Häufigkeitsverteilung kommt für gruppierte Daten das Histogramm zur Anwendung. Über jede Klasse ist entsprechend ihrer Klassenbreite eine Rechteckfläche zu zeichnen. Dabei verhalten sich die Flächeninhalte der Rechtecke proportional zu den einfachen Klassenhäufigkeiten. Die Flächenproportionalität kann wie folgt erreicht werden:

\(g_i=\frac{h_i}{\Delta_i}\) ist die absolute Häufigkeitsdichte.
\(\alpha_i=\frac{f_i}{\Delta_i}\) ist die relative Häufigkeitsdichte.

Der Flächeninhalt der Rechtecke entspricht somit \(g_i\cdot \Delta_i=\frac{h_i}{\Delta_i} \cdot \Delta_i=h_i\), falls die absoluten Häufigkeitsdichten verwendet werden und \(f_i\), falls die relativen Häufigkeitsdichten verwendet werden.

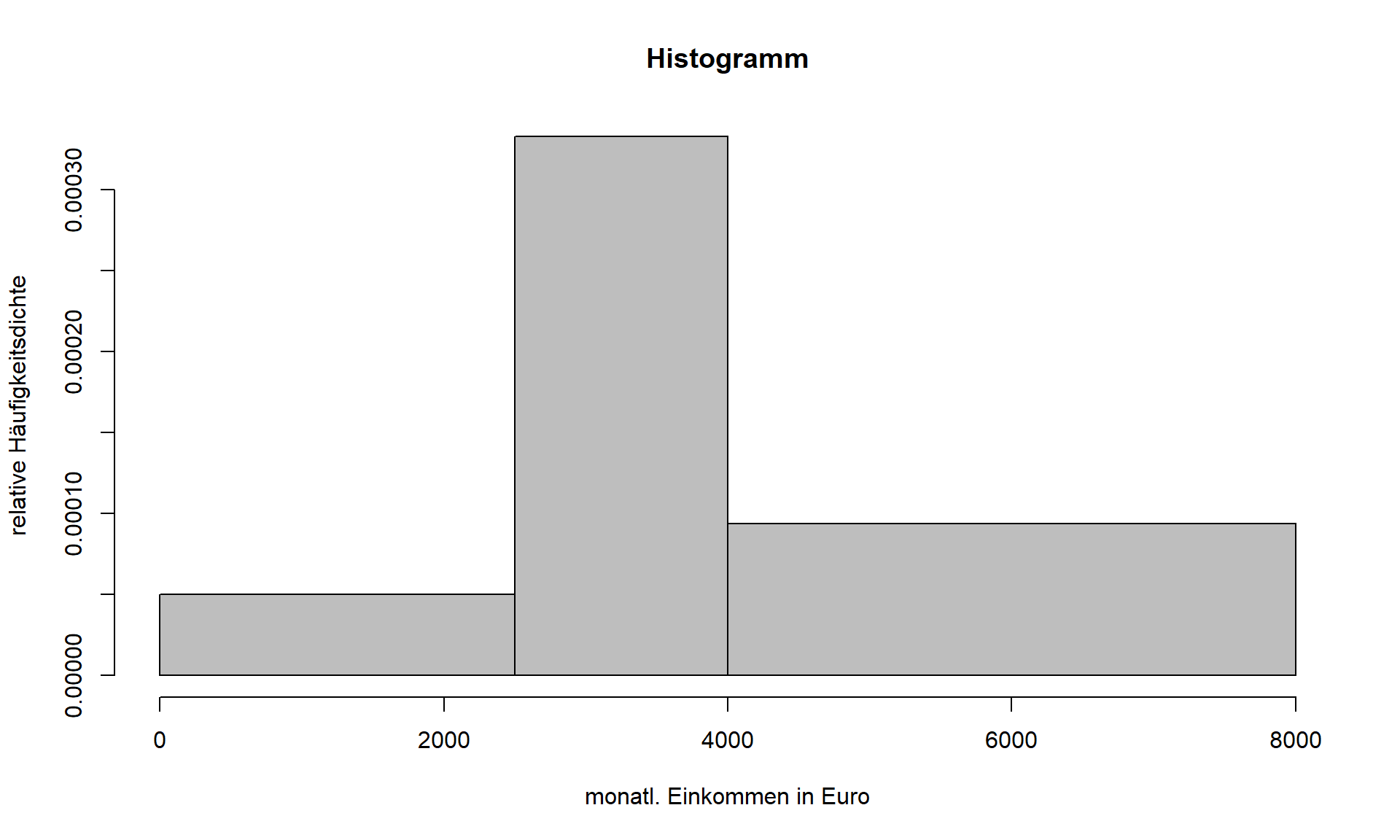
2.5: Histogramm Merkmal Monatseinkommen

Dem Histogramm liegt die Annahme der Gleichverteilung innerhalb der Klassen zugrunde. Teilt man beispielsweise die dritte Klasse über ihren Klassenmittelpunkt von 6000 in zwei Hälften, so ist klar zu erkennen, dass beide Flächen die gleiche Größe aufweisen müssen. Somit wird davon ausgegangen, dass 50% der Beobachtungen in die erste Hälfte fallen und die übrigen 50% in die zweite Hälfte. Die tatsächliche Häufigkeitsverteilung innerhalb der Klassen bleibt jedoch unbekannt. Anzumerken ist noch, dass die Häufigkeit, die einer einzelnen Ausprägung zuzuordnen ist, immer Null entspricht, da ein Punktwert keine Breite besitzt und die Fläche über diesem Punktwert somit 0 ist.

2.3.3 approximierende empirische Verteilungsfunktion

Aufgrund des Informationsverlustes beim Übergang von der Datenlage B zur Datenlage C, ist die genaue Verteilungsfunktion \(F(x)\) nicht bestimmbar. Mit Hilfe der Gleichverteilungsannahme innerhalb der Klassen, kann jedoch eine Näherungslösung für die unbekannte, wahre Verteilungsfunktion bestimmt werden. Diese Näherungslösung wird approximierende empirische Verteilungsfunktion \(\hat{F}(x)\) genannt. Diese lässt sich unter Verwendung der relativen Häufigkeitsdichten aus dem Histogramm gewinnen. Soll für einen bestimmten Wert \(x\) der Anteil der Beobachtungen angegeben werden, welche kleiner oder gleich \(x\) sind, so wird einfach die Histogrammfläche bis zu diesem Wert \(x\) bestimmt. Dies führt zu folgender Definition für die approximierende empirische Verteilungsfunktion \(\hat{F}(x)\):

\[\hat{F}(x) = \begin{cases} 0 & \mbox{für} \ \ x < a_0 \\ F_{i-1}+\frac{f_i}{\Delta_i}(x-a_{i-1}) &\mbox{für} \ \ a_{i-1}\leq x < a_{i}, \ \ \mbox{mit} \ \ i \in \{1,...,k\} \\ 1 &\mbox{für} \ \ a_k\leq x \end{cases}\]

Nachfolgend sind das Histogramm und die approximierende empirische Verteilungsfunktion für das Beispiel 2.4 zu sehen. Es wird den Fragen nachgegangen, wie groß der Anteil der Studierenden mit einem Einkommen bis 3000€, 1000€, 6000€ und 9000€ ist. Dieser Anteil entspricht jeweils der rot eingefärbten Fläche des Histogramms und kann über die Verteilungsfunktion abgelesen werden.

Im folgenden Video wird der Zusammenhang zwischen Histogramm und Verteilungsfunktion für das Zahlenbeispiel ausführlicher beleuchtet:

2.4 Grundtypen empirischer Verteilungen

Wichtige Grundtypen empirischer Häufigkeitsverteilungen sind in Abbildung 2.6 zu sehen. Häufig versucht man einen Datensatz einem dieser Grundtypen zuzuordnen. Dies kann über die Häufigkeitsverteilung in Form eine Stabdiagramms oder Histogramms erfolgen. Eine Zuordnung ist in vielen Fällen jedoch auch über statistische Kenngrößen möglich, die in den folgenden Kapiteln behandelt werden.

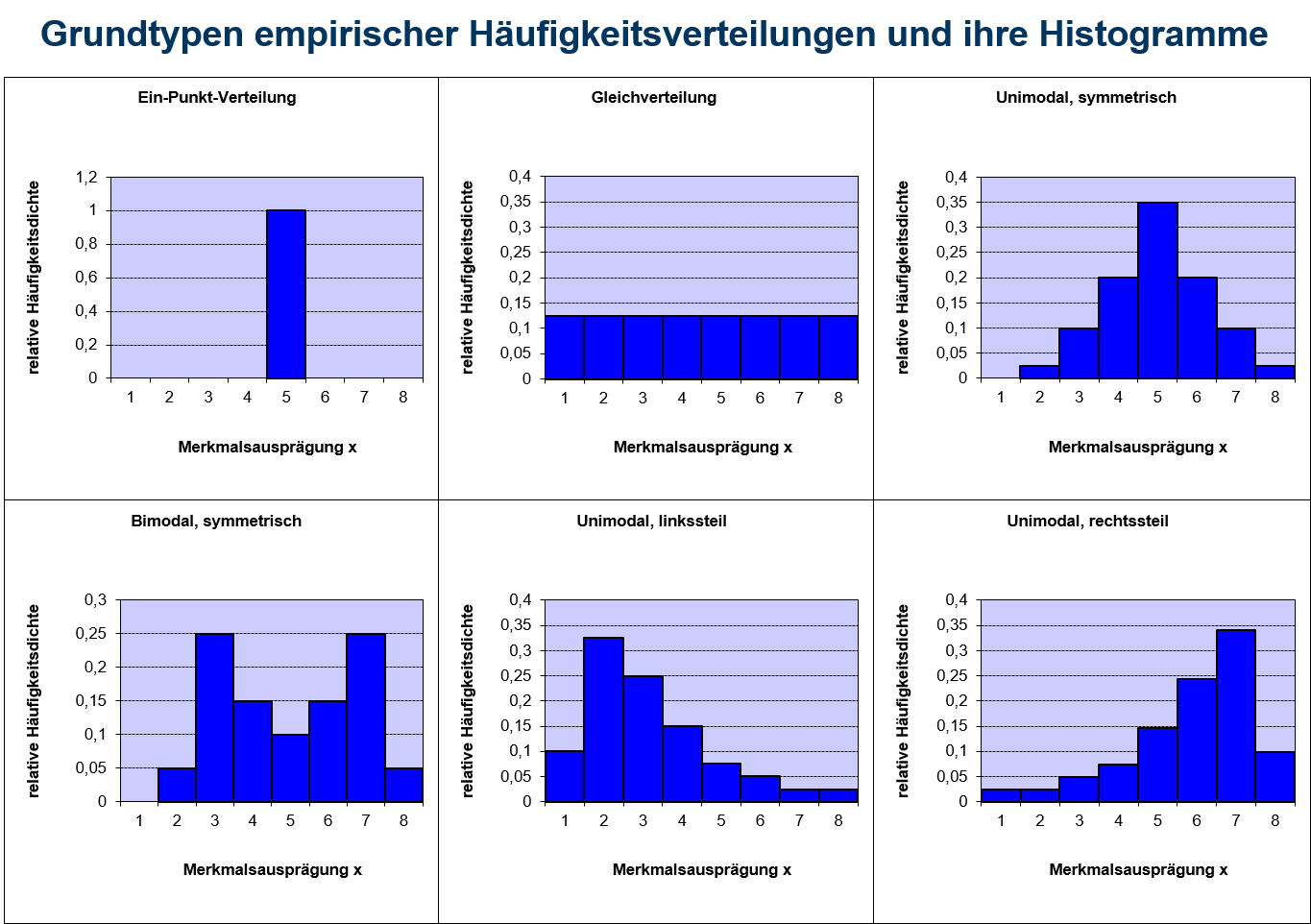
2.6: Grundtypen von Häufigkeitsverteilungen