Kapitel 5 Konzentrationsmessung

Unter Konzentration versteht man die (ungleiche) Verteilung der Merkmalssumme eines Erhebungsmerkmals auf die Merkmalsträger.

Bei einer Gleichverteilung der Merkmalssumme auf die Merkmalsträger spricht man von nicht vorhandener Konzentration. Diese Form der Gleichverteilung ist von der Gleichverteilung im Sinne einer Häufigkeitsverteilung abzugrenzen, bei der es um die Verteilung der Merkmalsträger auf die Merkmalsausprägungen geht. Das folgende Beispiel soll dies verdeutlichen:
Angenommen, ein Sixpack Bier wird von 2 Personen geleert. Eine Person trinkt 2 Flaschen, während die zweite Person 4 Flaschen trinkt. Im Sinne einer Häufigkeitsverteilung liegt dann eine Gleichverteilung vor, da die beiden Merkmalsausprägungen (2 und 4 Flaschen) jeweils einmal, also gleich häufig auftreten. Es liegt allerdings eine Konzentration vor, da die Flaschen nicht gleich auf die beiden Personen verteilt wurden. Wenn jeder 3 Flaschen erhält, so liegt keine Konzentration vor, da die Merkmalssumme von 6 Flaschen sich so gleichmäßig auf die Merkmalsträger verteilt. Eine nicht vorhandene Konzentration geht also immer mit einer Häufigkeitsverteilung in Form einer Einpunktverteilung einher.

Die Konzentrationsbetrachtung kann zeitpunktbezogen und somit statisch oder zeitraumbezogen und somit dynamisch erfolgen. Zudem ist zwischen absoluter und relativer Konzentration zu unterscheiden.
Wird für eine bestimmte absolute Zahl von Merkmalsträgern ihr Anteil an der Merkmalssumme angegeben, so spricht man von absoluter Konzentration.
Beispiel: Die drei größten Internetsuchmaschinen (Google, Bing, Yahoo) haben auf dem Markt für Desktopsuchen einen Marktanteil von zusammen rund 96%.
Wird für einen bestimmten Anteil von Merkmalsträgern ihr Anteil an der Merkmalssumme angegeben, so spricht man von relativer Konzentration.
Beispiel: Auf die reichsten 10% der Bevölkerung in Deutschland entfallen rund 60% des Gesamtvermögens.

Im Folgenden werden ausschließlich Maße für die statische, relative Konzentrationsmessung betrachtet. Durch wiederholte statische Konzentrationsmessungen im Zeitablauf lässt sich allerdings ein dynamisches Bild erzeugen.

5.1 Lorenzkurve

Die Lorenzkurve veranschaulicht die Konzentration für ein Merkmal durch Zuordnung der kumulierten relativen Häufigkeiten zu den kumulierten Anteilen an der Merkmalssumme. Grundvoraussetzung zur Bildung von Anteilen an der Merkmalssumme ist ein mindestens verhältnisskaliertes Merkmal, mit ausschließlich nicht-negativen Merkmalsausprägungen und einer sinnvoll interpretierbaren Merkmalssumme. Um zu gehaltvollen Aussagen gelangen zu können, muss die Analyse in einer für das Merkmal sortierten Betrachtung erfolgen.
So hat die Aussage, “Die umsatzschwächsten 40% der Unternehmen weisen einen Marktanteil von 25% auf”, einen wesentlich höheren Aussagegehalt als die Aussage, “Eine Gruppe beliebig ausgewählter Unternehmen, welche 40% der gesamten Unternehmen ausmachen, weist einen Marktanteil von 30% auf”.
In Abhängigkeit der Datenlage ist die Lorenzkurve wie folgt zu erstellen:

5.1.1 Datenlage A

Den Ausgangspunkt bilden die in aufsteigender Reihenfolge sortierten Beobachtungen, also die geordnete Urliste: \[x_{(1)}\leq x_{(2)} \leq...\leq x_{(n)} \] Die Merkmalssumme \(S\) bestimmt sich dann aus Summation aller Beobachtungen. \[S=\sum_{i=1}^nx_{(i)}\] Mit \(g_i\) wird dann der Anteil an der Merkmalssumme von Merkmalsträger \((i)\) in der geordneten Urliste bezeichnet. \[g_i=\frac{x_{(i)}}{S}\] Die kumulierten Anteile an der Merkmalssumme lauten dann: \[G_i=\sum_{j=1}^ig_j\] Die zugehörigen kumulierten relativen Häufigkeiten werden bestimmt aus: \[F_i=\frac{i}{n}\] Durch die Koordinaten \((0,0),(F_1,G_1),...,(F_n,G_n)\) wird dann ein Streckenzug in ein Koordinatensystem gezeichnet, welcher die Lorenzkurve darstellt. Zudem ist durch die Punkte \((0,0),(1,1)\) eine Diagonale als Referenz einzuzeichnen, welche einer Lorenzkurve bei nicht vorhandener Konzentration entspricht.

In Tabelle 5.1 werden für 5 Unternehmen einer Branche deren Umsätze im vergangenen Monat in Tsd. € betrachtet.

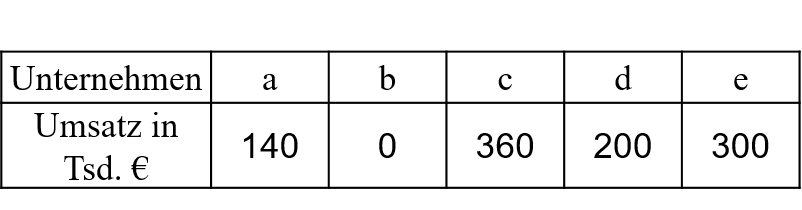
5.1: Zahlenbeispiel Umsätze

Die Lorenzkurve mit der zugehörigen Arbeitstabelle findet sich in Abbildung 5.2.
Im folgenden Video werden die einzelnen Arbeitsschritte erläutert:

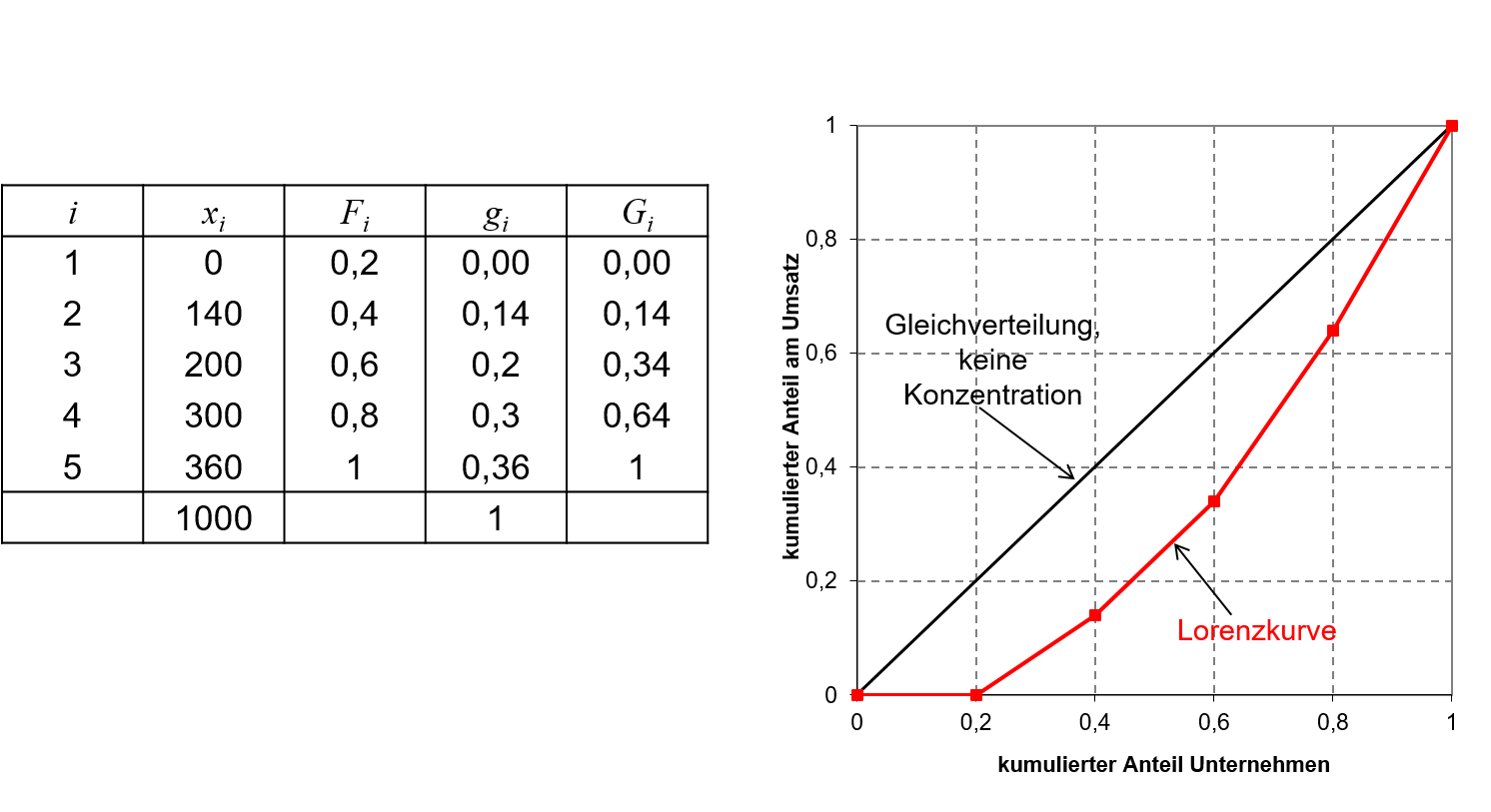
5.2: Zahlenbeispiel Umsätze

Eine Gleichverteilung der Merkmalssumme auf die Merkmalsträger würde bedeuten, dass es nur einen Beobachtungswert gibt, der \(n\)-mal auftritt. Im Falle von 5 Unternehmen mit einem Branchenumsatz von insgesamt 1000 Tsd. €, würde dies bedeuten, dass jedes Unternehmen einen Umsatz von 200 Tsd. € aufweist. Die kumulierten relativen Häufigkeiten \(F_i\) würden in diesem Fall mit den kumulierten Anteilen an der Merkmalssumme \(G_i\) übereinstimmen, denn für einen bestimmten über alle Unternehmen gleichen Umsatz \(c\) würde gelten:
\[S=n\cdot c \ \ \mbox{und} \ \ g_i=\frac{c}{n\cdot c}=\frac{1}{n}\] Somit folgt: \[G_i=\sum_{j=1}^i\frac{1}{n}=\frac{i}{n}=F_i\] Die Lorenzkurve verläuft somit als Diagonale, falls keine Konzentration vorliegt.
Durch die Sortierung in aufsteigender Reihenfolge können Lorenzkurven die Diagonale niemals schneiden. Je weiter die Lorenzkurve von der Diagonalen entfernt ist, umso stärker fällt die Konzentration aus. Aufgrund der Sortierung der Beobachtungen können Lorenzkurven auch niemals oberhalb der Diagonalen verlaufen, denn \[G_i\leq F_i \ \ \forall \ \ i\]

5.1.2 Datenlage B

Zu jeder Merkmalsausprägung \(x_i\) werden die Koordinaten \((F_i, G_i)\) bestimmt, damit die Lorenzkurve gezeichnet werden kann.
Zuvor muss zu jedem \(x_i\) der Anteil an der Merkmalssumme \(g_i\) bestimmt werden. \[g_i=\frac{h_i \cdot x_i}{S} \ \ \mbox{mit} \ \ S=\sum_{i=1}^mh_i\cdot x_i\] Im folgenden Beispiel werden für 40 Passagiere eines Kreuzfahrtschiffs fünf unterschiedliche Tagesausflüge angeboten, welche für die Passagiere mit zusätzlichen Kosten und somit für die Reederei mit Umsätzen in Höhe von 10€, 25€, 30€, 50€ bzw. 90€ verbunden sind. Die Lorenzkurve veranschaulicht die Verteilung der Umsätze auf die Passagiere. So kann aus der Kurve beispielsweise abgelesen werden \((F_3=0,9; \ G_3=0,72)\) , dass auf die 10% mit den teuersten Tagesausflügen 28% der Umsätze entfallen.

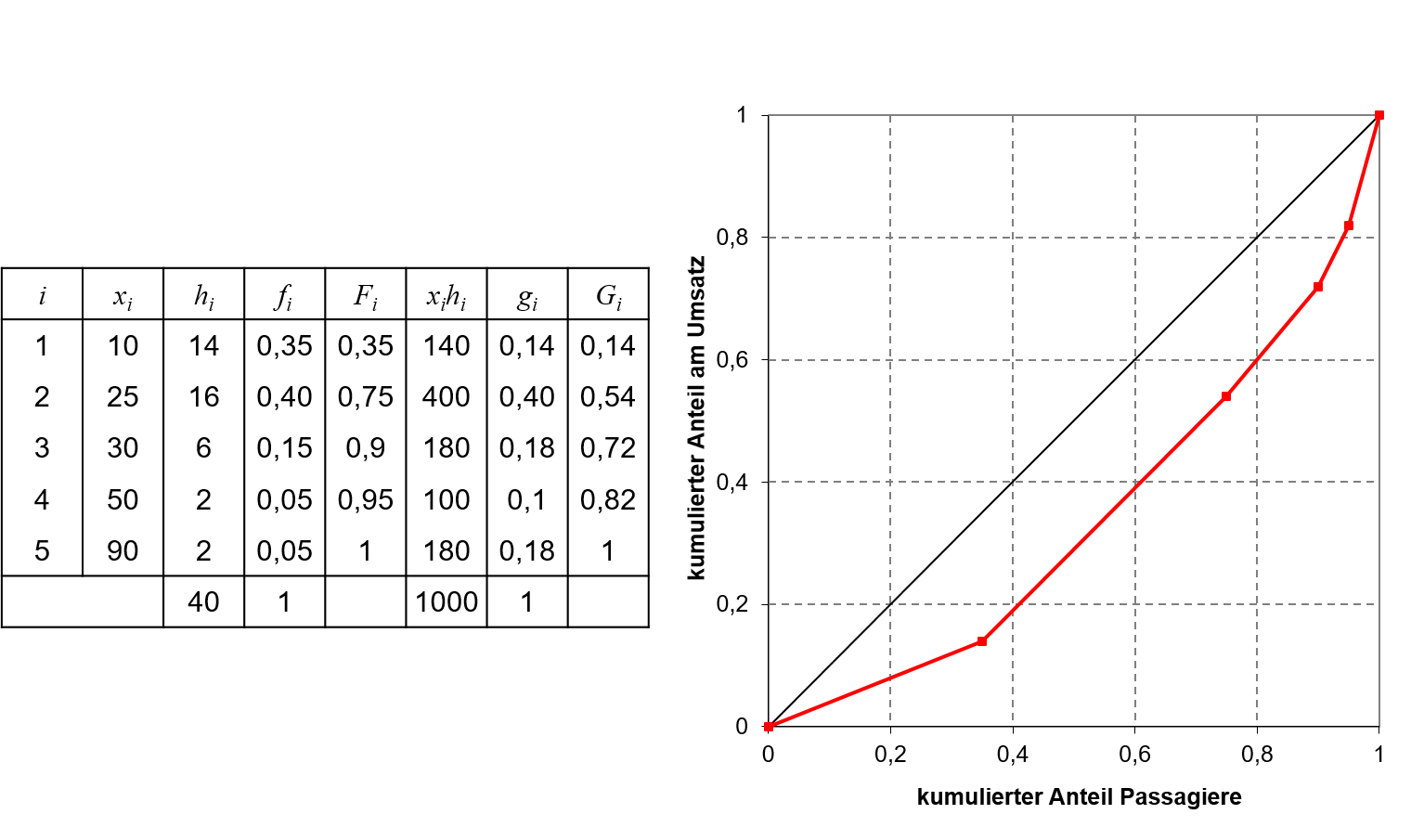
5.3: Umsätze Tagesausflüge

5.1.3 Datenlage C

Zu jeder Klasse werden wiederum die Koordinaten \((F_i, \widehat{G}_i)\) bestimmt, wobei mit \(\widehat{G}_i\) ein Näherungswert für die kumulierten Anteile an der Merkmalssumme bezeichnet wird. Die Klassenanteile an der Merkmalssumme \(\widehat{g}_i\) werden zuvor mit Hilfe der Klassenmitten \(x_i\) näherungsweise bestimmt. \[\widehat{g_i}=\frac{h_i \cdot x_i}{\widehat{S}} \ \ \mbox{mit} \ \ \widehat{S}=\sum_{i=1}^k h_i \cdot x_i\] Mit dem Datensatz aus Tabelle 5.4 wird für landwirtschaftliche Betriebe das Merkmal Betriebsgröße in ha betrachtet. Für die offene Klasse wurde eine willkürliche Klassenobergrenze von 1000 festgelegt, um einen Klassenmittelpunkt \(x_i\) bestimmen zu können.

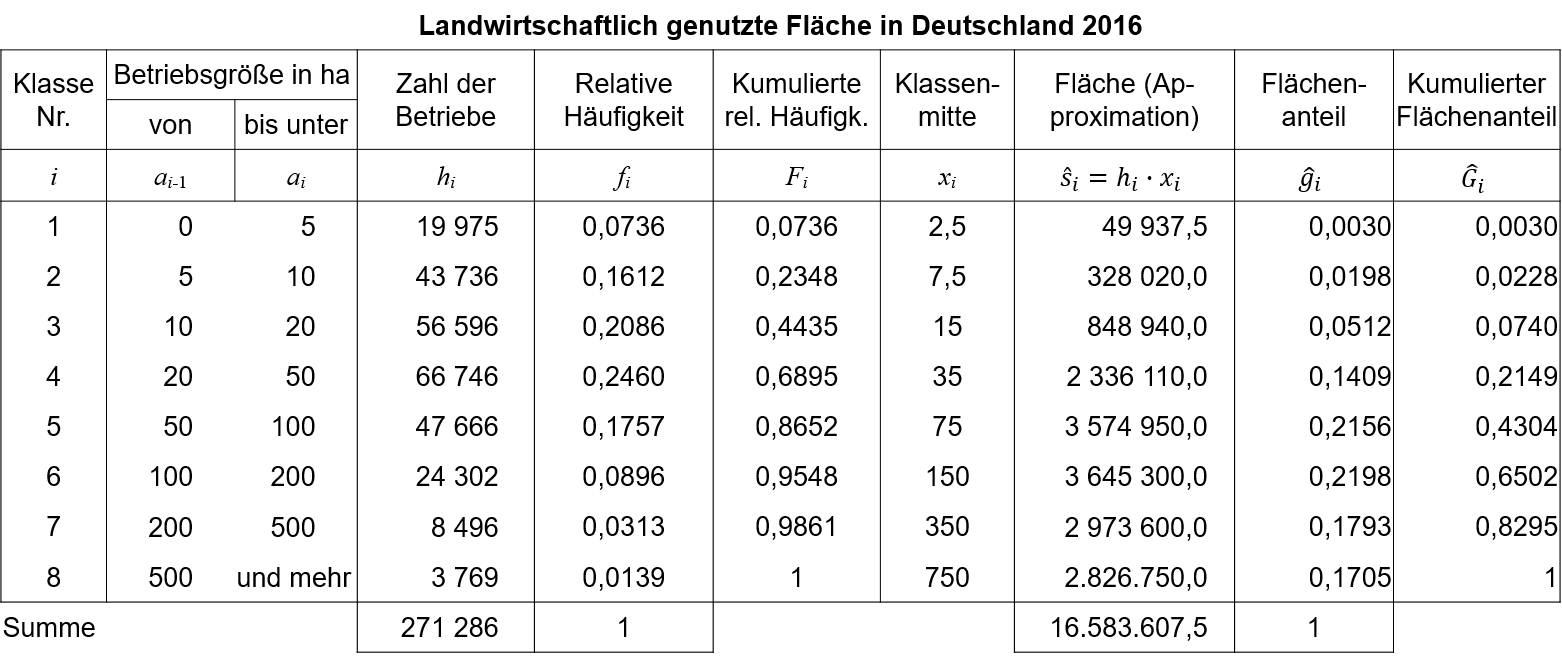
5.4: landwirschaftlich genutzte Fläche in Deutschland, Quelle: Statistisches Bundesamt

Die Lorenzkurve zu Tabelle 5.4 wird in Abbildung 5.5 gezeigt. Aus der Kurve kann abgelesen werden, dass auf die kleinere Hälfte der Betriebe kaum mehr als 10% der gesamten landwirtschaftliche Fläche entfällt.

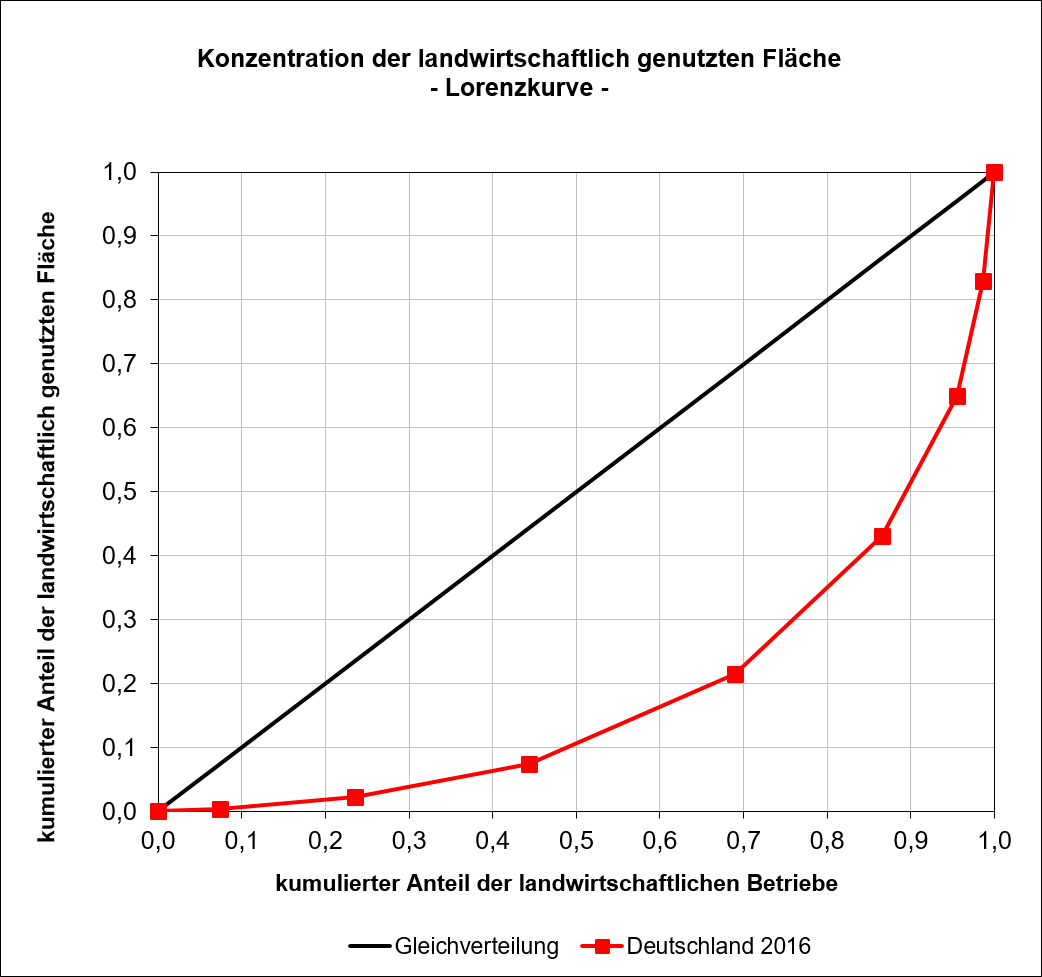
5.5: Lorenzkurve, landwirschaftlich genutzte Fläche in Deutschland, Quelle: Statistisches Bundesamt

Die Lorenzkurven in Abbildung 5.6 zeigen für das Bundesland Rheinland-Pfalz deutlich auf, welcher Konzentrationsprozess in der Landwirtschaft im Zeitraum von 1949 bis 2009 stattgefunden hat. Die Lorenzkurven entfernen sich mit zunehmender Zeit immer weiter von der Diagonalen und zeigen somit deutlich eine Zunahme der Konzentration, also eine zunehmende Ungleichverteilung der landwirtschaftlichen Fläche auf die Betriebe, auf.

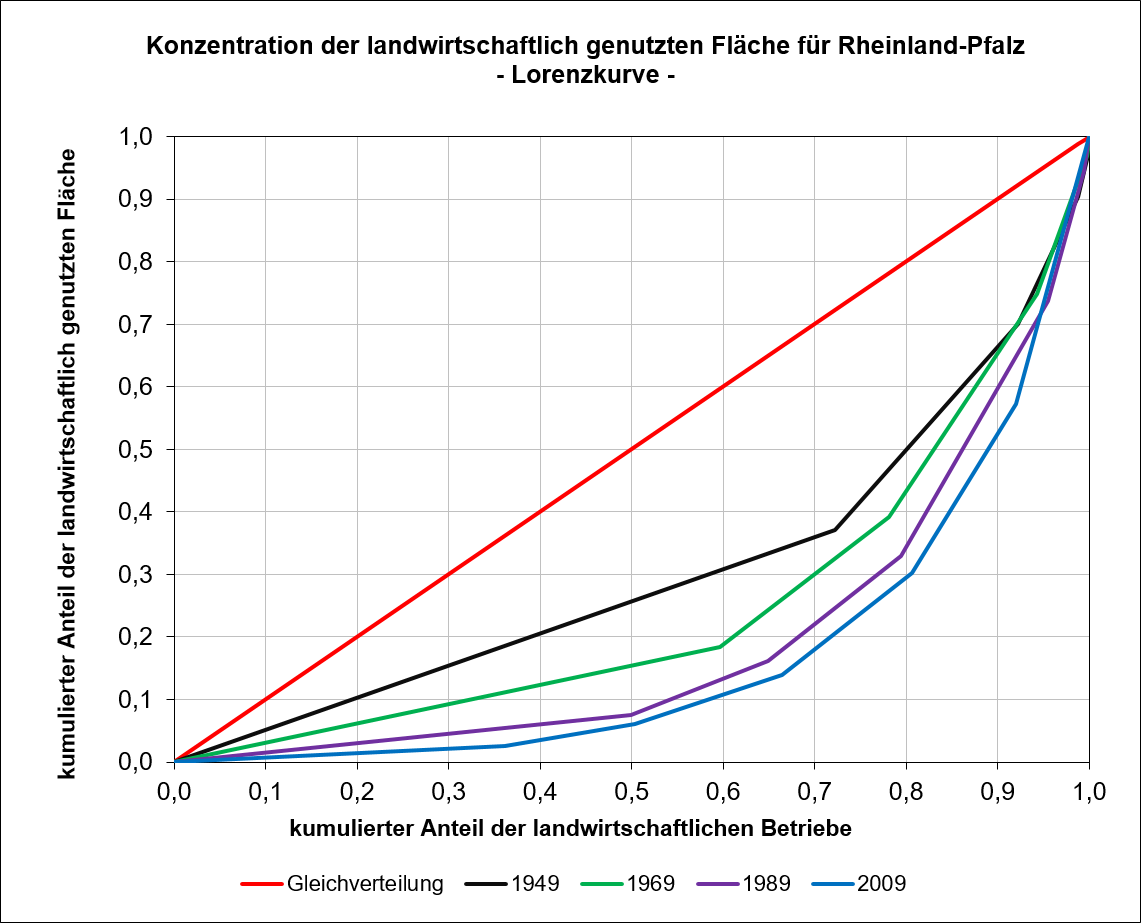
5.6: Lorenzkurve, landwirschaftlich genutzte Fläche in Rheinland-Pfalz, Quelle: Statistisches Bundesamt

Überhaupt sind Lorenzkurven für Vergleiche gut geeignet. Dies betrifft nicht nur Vergleiche im Zeitablauf, sondern auch Vergleiche für gleiche Merkmale unterschiedlicher Grundgesamtheiten. So könnte man etwa die Ungleichverteilung der Einkommen für verschiedene Länder durch Lorenzkurven in einer Zeichnung abbilden. Allerdings kann dies auch sehr schnell unübersichtlich werden, wenn viele Kurven einzuzeichnen sind oder sich die Lorenzkurven schneiden. Als Kriterium zur Konzentrationsmessung wird in solchen Situationen häufig auf den Gini-Koeffizienten zurückgegriffen, der die Konzentration in Form einer einzigen Kennzahl angibt.

5.2 Gini-Koeffizient

Der Gini-Koeffizient ist eine statistische Maßzahl, welche aus der Lorenzkurve gewonnen wird. Der Gini-Koeffizient entspricht dem Zweifachen der Fläche zwischen der Diagonalen und der Lorenzkurve.
Die Fläche zwischen der Diagonalen und der Lorenzkurve wird in Abbildung 5.7 mit \(M\) bezeichnet. Diese wird nicht direkt ermittelt, sondern es wird zunächst die Fläche \(L\) bestimmt, welche sich unter der Lorenzkurve befindet. Da die Fläche unter der Diagonalen offensichtlich 0,5 entspricht, kann die Fläche M dann berechnet werden als \(M=0,5-L\), so dass für den Gini-Koeffizienten \(c_G\) gilt: \[c_G=2\cdot M=1-2\cdot L , \ \ c_G\in \left[ 0,\frac{n-1}{n}\right] \] Je größer die Konzentration mit zunehmender Fläche \(M\) ausfällt, umso größere Werte nimmt der Gini-Koeffizient an. Dieser ist in Abhängigkeit der Beobachtungen \(n\) jedoch auf \(\frac{n-1}{n}\) nach oben beschränkt, so dass in großen Datensätzen für \(c_G\) Werte knapp unter 1 möglich sind.

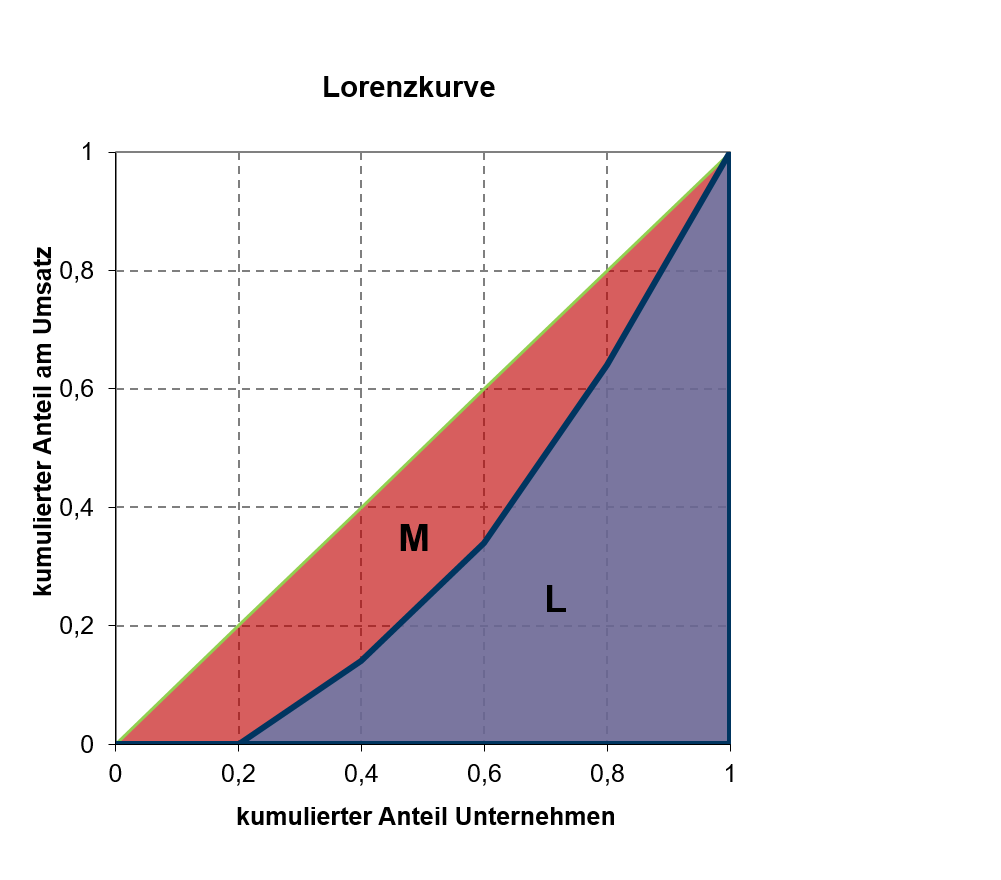
5.7: zu berechnende Flächen

Die für den Gini-Koeffizienten benötigte Fläche \(L\) kann als Summe der Trapezflächen unter der Lorenzkurve bestimmt werden, so dass man für die drei Datenlagen die folgenden Berechnungsvorschriften erhält:

Datenlage A \[L=\frac{1}{2n}\sum_{i=1}^n(G_{i-1}+G_i), \ \ \mbox{mit} \ \ G_0=0 \] Datenlage B \[L=\frac{1}{2n}\sum_{i=1}^m h_i\cdot (G_{i-1}+G_i), \ \ \mbox{mit} \ \ G_0=0 \] Datenlage C \[L=\frac{1}{2n}\sum_{i=1}^k h_i\cdot (\widehat{G}_{i-1}+\widehat{G}_i), \ \ \mbox{mit} \ \ \widehat{G}_0=0 \]

Abbildung 5.8 zeigt exemplarisch eine Lorenzkurve mit den zugehörigen Trapezflächen unter der Kurve, deren Flächeninhalte mit Hilfe der vorgestellten Formeln ermittelt werden.

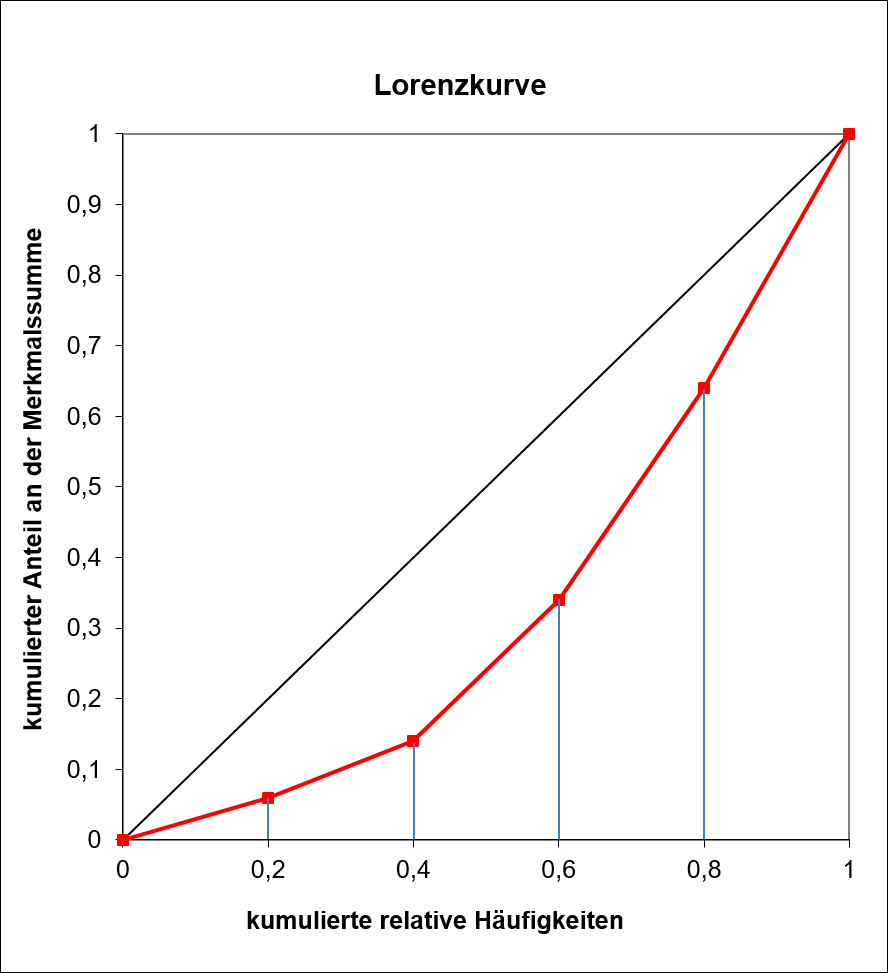
5.8: Lorenzkurve, Trapezflächen

Die Herleitung der Formeln für den Gini-Koeffizienten, über die Trapezflächen unter der Lorenzkurve, wird im folgenden Video erläutert:

5.3 normierter Gini-Koeffizient

Der Gini-Koeffizient \(c_G\) ist auf das Intervall von \([0, \ \frac{n-1}{n}]\) beschränkt, dessen obere Schranke von der Anzahl der Beobachtungen abhängt. Ein Vergleich von Konzentrationen anhand des Gini-Koeffizienten für abweichende Beobachtungszahlen kann somit insbesondere bei kleinen Datensätzen problematisch sein. Das Maximum liegt für den Gini-Koeffizienten im Falle von \(n=3\) beispielsweise bei \(c_G=0,\overline{6}\) und bei \(n=8\) bei \(c_G=0,875\). Um für kleine Datensätze unterschiedlichen Umfangs dennoch sinnvolle Vergleiche der Konzentration anstellen zu können, sollte besser auf den normierten Gini-Koeffizienten \(nc_G\) zurückgegriffen werden.

\[nc_G=\frac{n }{n-1}\cdot c_G, \ \ nc_G \in [0; \ 1] \]

Für das Beispiel aus Tabelle 5.1 wird ein normierter Gini-Koeffizient von \(nc_G=0,44\) ermittelt.

Die Berechnung kann im folgenden Video nachvollzogen werden: