Kapitel 1 Merkmale und Merkmalsträger

Was ist Statistik? kurze Erläuterung im folgenden Videoclip:

Bei jeder Erhebung von Daten ist zwischen Merkmalsträgern und Merkmalen zu unterscheiden. Befragt man die Studierenden eines Kurses an der Uni nach ihrem Alter, so sind die Studierenden die Merkmalsträger und das Alter ist das Merkmal der Erhebung. Die Studierenden sind also Träger der Information(en). Dabei können Merkmalsträger auch Objekte (z.B. Häuser mit dem Merkmal Wohnfläche in qm) oder Ereignisse (z.B. Banküberweisungen mit dem Merkmal Betrag in €) sein. Die Menge aller Merkmalsträger einer Untersuchung wird dann als Grundgesamtheit (statistische Masse) bezeichnet. Die Grundgesamtheit lässt sich nach sachlichen, räumlichen und zeitlichen Kriterien exakt abgrenzen. Z.B. könnten für eine Untersuchung Studierende der Fakultät für Wirtschaftswissenschaft (sachlich), an der Ruhr-Universität Bochum (räumlich), im Wintersemester 2020/2021 (zeitlich) befragt werden. Mit Merkmalsausprägungen werden die möglichen, unterscheidbaren Erscheinungsformen eines Merkmals bezeichnet. Beobachtungswerte sind Merkmalsausprägungen, die tatsächlich in einem Datensatz auftreten.

1.1 Bestands- und Bewegungsmasse

Grundgesamtheiten (statistische Massen) werden nach Bestandsmassen und Bewegungsmassen unterschieden. Ausschlaggebend ist, ob die Merkmalsträger der statistischen Masse im Hinblick auf ihre zeitliche Abgrenzung eine Verweildauer aufweisen. Anstelle von Verweildauer könnte man auch von Lebensdauer sprechen. Die zeitliche Abgrenzung der Bestandsmasse erfolgt dann mit der Angabe eines Zeitpunktes. Die Bewegungsmasse wird hingegen zeitlich über die Angabe eines Zeitraumes abgegrenzt.

Bestandsmasse

Die Merkmalsträger einer Bestandsmasse können zu einem Zeitpunkt erfasst werden, da diese eine Lebensdauer aufweisen. Es ließen sich z.B. die eingeschriebenen Studierenden zu einer bestimmten Uhrzeit am 01.11.2020 erfassen. Man spricht dann von Bestandsgrößen.

Bewegungsmasse

Die Merkmalsträger einer Bewegungsmasse können nur innerhalb eines Zeitraums erfasst werden. So z.B. Studierende, die sich im September 2020 immatrikuliert haben. Man spricht hier von Stromgrößen. Natürlich weisen die Studierenden selber immer eine Lebensdauer auf. Ausschlaggebend ist aber, wie die relevante Menge zeitlich abgegrenzt wird. Die Immatrikulation stellt ein Ereignis dar und besitzt keine Lebensdauer.

Bestandsgrößen werden im Zeitablauf durch Stromgrößen verändert. So verändert sich die Masse der eingeschriebenen Studierenden im Zeitablauf durch Immatrikulationen und Exmatrikulationen.

1.2 Attribute statistischer Merkmale

häufbare und nicht häufbare Merkmale

Ein Merkmal wird als häufbar bezeichnet, falls es möglich ist, dass ein Merkmalsträger gleichzeitig mehrere Merkmalsausprägungen aufweisen kann. Betrachtet man z.B. das Alter eines Studierenden, so ist dieses natürlich nicht häufbar. Das Merkmal Studiengang ist hingegen häufbar, da eine Person auch mehrere Studiengänge belegen kann.

zeitlich, sachlich, räumlich

Merkmale können zeitlicher (Wann?), sachlicher (Was?) und räumlicher (Wo?) Natur sein. Beispiele sind das Geburtsdatum, der Studiengang und der Wohnort.

qualitativ, quantitativ

Mit qualitativen Merkmalen kann nicht sinnvoll gerechnet werden. Die Merkmalsausprägungen sind originär meist nicht numerisch, allerdings können Codierungen erfolgen. Auch wenn dann numerische Werte vorliegen, wie z.B. Postleitzahlen oder Telefonnummern, so kann mit diesen nicht sinnvoll gerechnet werden.

Quantitative Merkmale sind hingegen numerisch und es können zumindest sinnvoll Differenzen zwischen den Merkmalsausprägungen bestimmt werden. Beispiele sind das Alter, oder das Einkommen.

stetig, diskret

Innerhalb der quantitativen Merkmale unterscheidet man zwischen stetigen und diskreten Merkmalen. Kennzeichnend für diskrete Merkmale ist die Abzählbarkeit der Menge möglicher Merkmalsausprägungen. Stammen die Merkmalsausprägungen also aus der Menge der natürlichen Zahlen oder aus der Menge der rationalen Zahlen, so handelt es sich um ein diskretes Merkmal. Für stetige Merkmale sind als Merkmalsausprägungen Intervalle aus den reellen Zahlen zugelassen. Anders als bei den natürlichen Zahlen oder den rationalen Zahlen, lässt sich für zwei reelle Zahlen immer eine weitere Zahl finden, die zwischen den beiden Zahlen liegt. Beispiele für diskrete Merkmale sind die Zahl der Fachsemester und das Geburtsdatum. Beispiele für stetige Merkmale sind Gewicht und Körpergröße. Qualitative Merkmale weisen immer eine abzählbare Menge möglicher Merkmalsausprägungen auf und sind daher diskret. Die Attribute von Merkmalen sowie deren Zusammenhänge werden in Abbildung 1.1 zusammengefasst.

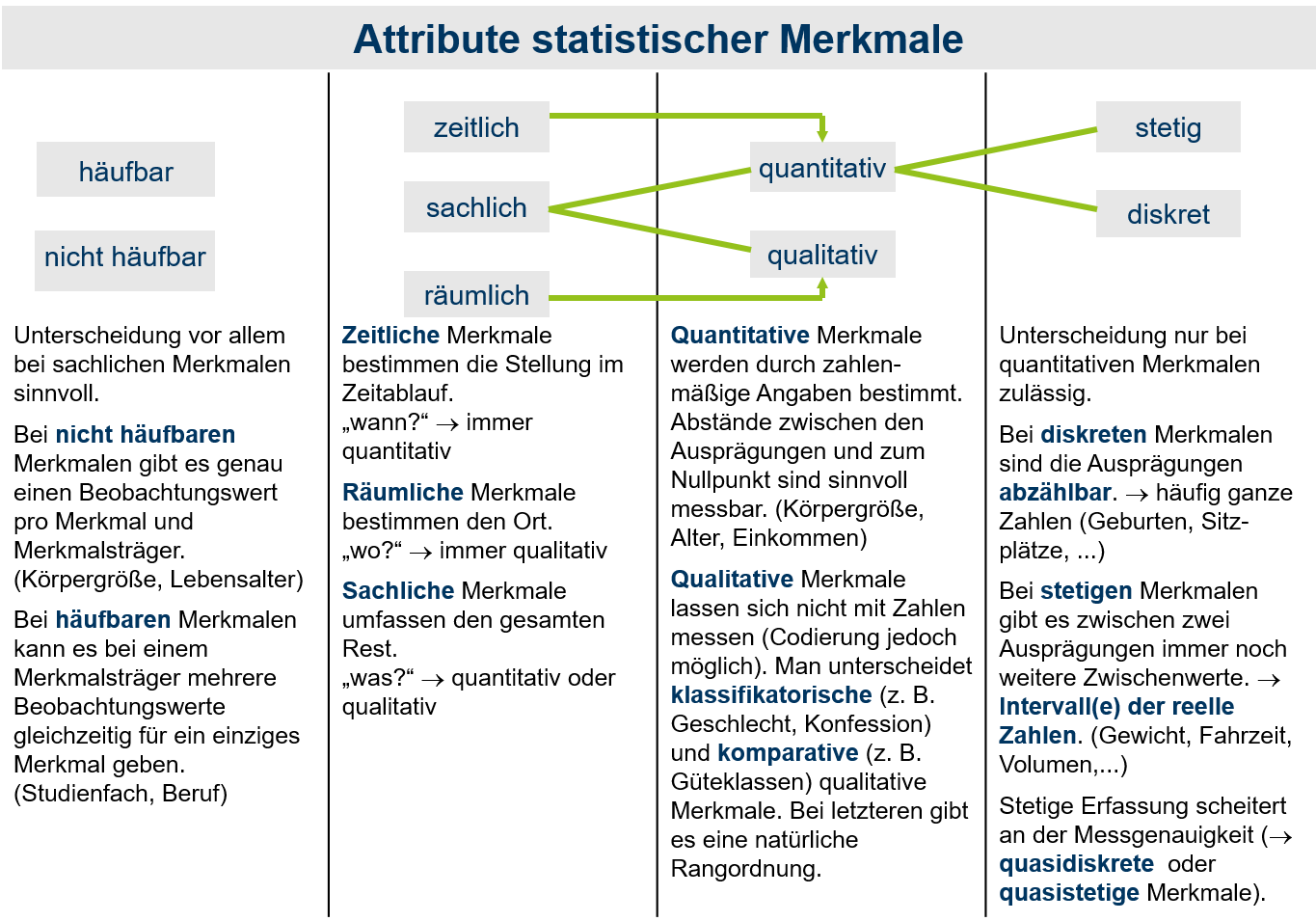
1.1: Attribute von Merkmalen

Videoclip zu Attribute statistischer Merkmale

1.3 Skalenniveau

Das Skalenniveau eines Merkmals ist ausschlaggebend dafür, welche statistischen Auswertung für das Merkmal vorgenommen werden können. Man unterscheidet zunächst wieder zwischen qualitativen und quantitativen Merkmalen und trifft dann weitere Unterscheidungen innerhalb der beiden Gruppen.

1.3.1 qualitative Skalen

Nachdem ein Merkmal als qualitativ klassifiziert wurde, ist für die weitere Zuordnung ausschlaggebend, ob eine natürliche Rangfolge der Merkmalsausprägungen existiert.

Nominalskala

Die Merkmalsausprägungen nominalskalierter Merkmale unterliegen keiner natürlichen Rangfolge. So können für das Merkmal Haarfarbe beispielsweise die möglichen Ausprägungen beliebig angeordnet werden.

Ordinalskala

Ordinalskalierte Merkmale weisen eine natürliche Rangfolge auf. Nach objektiven Maßstäben gibt es somit eine klare Sortierung, z.B. nach besser/schlechter oder größer/kleiner. Beispiele sind Güteklassen oder Schulnoten. Codierungen ordinalsklaierter Merkmale führen zu keiner Änderung des Skalenniveaus. Die Codierung der Schulnoten sehr gut, gut, usw. in 1,2, usw. führt also nicht dazu, dass das Merkmal quantitativ wird. Bei einem quantitativen Merkmal wären die Abstände zwischen den Ausprägungen 1 und 2 sowie 2 und 3 als gleichwertig anzusehen, was bei Schulnoten aber nicht der Fall ist.

1.3.2 quantitative Skalen

Nachdem ein Merkmal als quantitativ klassifiziert wurde, sind für die weitere Zuordnung der Nullpunkt und die Maßeinheit der Skala ausschlaggebend. Ein Nullpunkt kann willkürlich festgelegt sein oder es existiert ein natürlicher Nullpunkt. Ein natürlicher Nullpunkt ist sachlogisch entweder als absoluter Nullpunkt und somit als kleinstmöglicher Wert, so z.B. bei Temperaturangaben in Kelvin oder mit “Nichts” gleichzusetzen, so z.B. bei der Betrachtung des Kontostands. Von einer natürlichen Maßeinheit ist die Rede, wenn die Merkmalsausprägungen Stückzahlen darstellen und somit keinerlei Einheit mit anzugeben ist andernfalls handelt es sich um willkürliche Maßeinheiten, wie z.B. beim Einkommen, welches in einer bestimmten Währung anzugeben ist.

Intervallskala

Sind der Nullpunkt und die Maßeinheit der Skala willkürlich festgelegt, so handelt es ich um ein intervallskaliertes Merkmal. Beispielsweise ist die Temperatur gemessen in Grad Celsius intervallskaliert.

Aufgrund des willkürlichen Nullpunktes lassen sich für intervallskalierte Merkmale keine sinnvollen Aussagen aus der Bildung von Verhältnissen ableiten. So macht die Aussage keinen Sinn, dass eine Temperatur von 20°C doppelt so warm ist, wie eine Temperatur von 10°C. Denn rechnet man die beiden Temperaturen mit \(y°F=32+1,8 \cdot x°C\) in Grad Fahrenheit um, resultieren die Temperaturen von 68°F und 50°F. Ganz offensichtlich ist aber 68°F nicht das Doppelte von 50°F. Im Rahmen der Skalentransformation kam es also zu einer Verschiebung des Nullpunktes. Die Fahrenheitskala verwendet als Nullpunkt die tiefste Temperatur, die mit einer Mischung aus Eis, Wasser und Salmiak erreicht werden kann und der Gefrierpunkt des Wassers liegt bei dieser Skala bei 32°F.

Verhältnisskala

Namensgebend für verhältnisskalierte Merkmale ist, dass die Bildung von Verhältnissen und die Ableitung von Aussagen sinnvoll möglich ist. Ursächlich ist der natürliche Nullpunkt, den verhältnisskalierte Merkmale aufweisen müssen. Die Maßeinheit bleibt willkürlich. Skalentransformationen haben zur Beibehaltung des Skalenniveaus somit über einen Umrechnungsfaktor zu erfolgen, ohne dass es zu einer Nullpunktverschiebung kommt, wie es beispielsweise bei der Umrechnung von Währungen der Fall ist.

Absolutskala

Sofern die Merkmalsausprägungen Stückzahlen darstellen, handelt es sich um eine natürliche Maßeinheit und das Merkmal ist absolutskaliert. Der Nullpunkt ist in diesem Fall immer natürlich.

Die wesentlichen Unterscheidungskriterien sind für die fünf Skalen in Abbildung 1.2 zusammengefasst.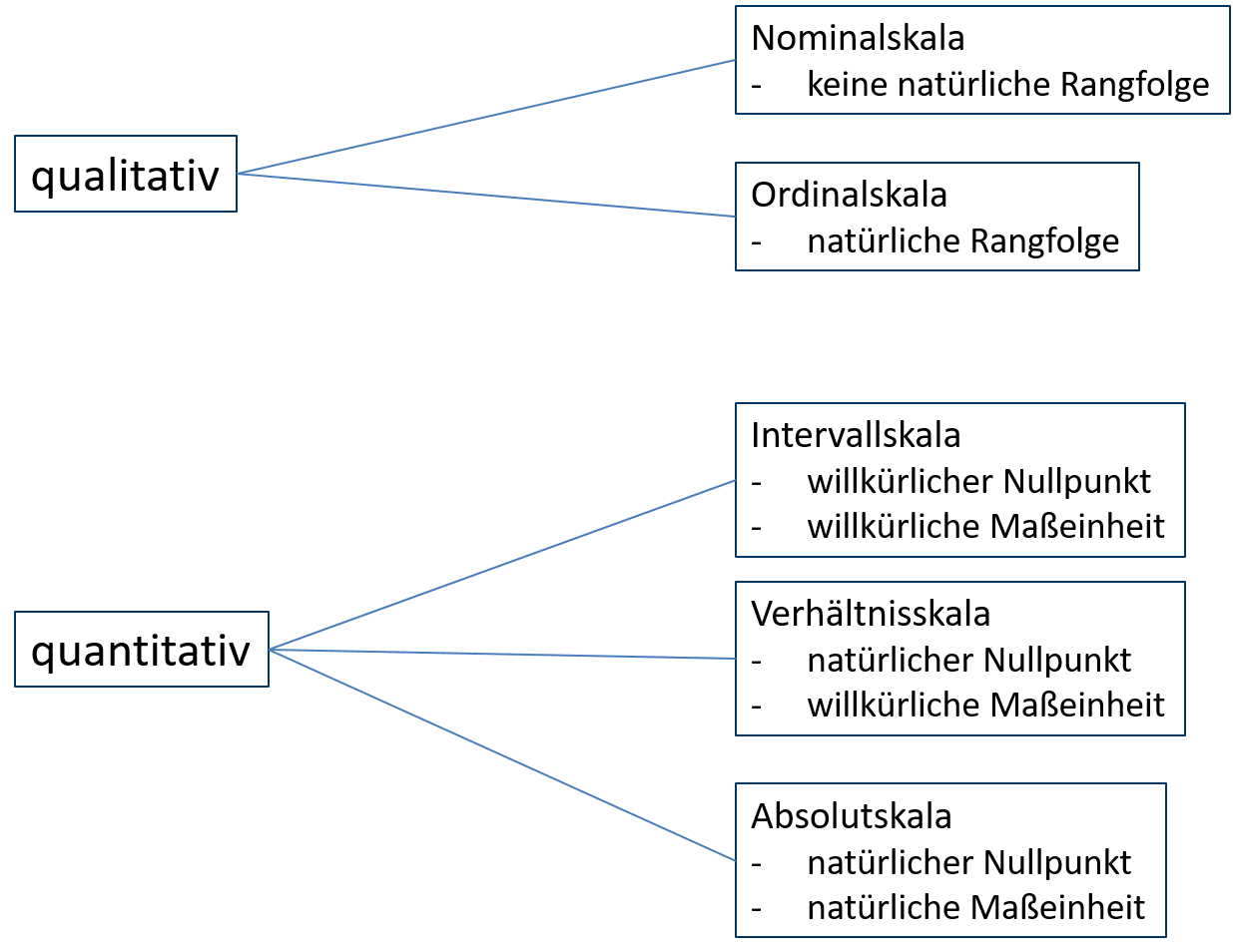

1.2: Unterscheidungskriterien Skalenniveau

Im folgenden Video werden zu den fünf Skalen einige Beispiele betrachtet.

Übungsfragen

1.3.3 hierarchische Anordnung

Abbildung 1.3 zeigt auf, welche Skalentransformationen zulässig sind, wenn das zugrundeliegende Skalenniveau nach der Transformation beibehalten werden soll. Die dargestellte Anordnung ist auch mit Blick auf statistische Auswertungen von großer Bedeutung. Es ist festzuhalten, dass statistische Maße, welche für ein bestimmtes Skalenniveau bestimmt werden könnnen, auch für alle folgenden Skalenniveaus bestimmt werden können. Beispielsweise kann das arithmetische Mittel erst ab Intervallskalenniveau sinnvoll bestimmt werden. Somit kann das arithmetische Mittel also auch für verhältnisskalierte und absolutskalierte Merkmale sinnvoll bestimmt werden. Einen Mittelwert aus Postleitzahlen zu bestimmen, macht hingegen keinen Sinn, auch wenn dies rechnerisch natürlich möglich ist.

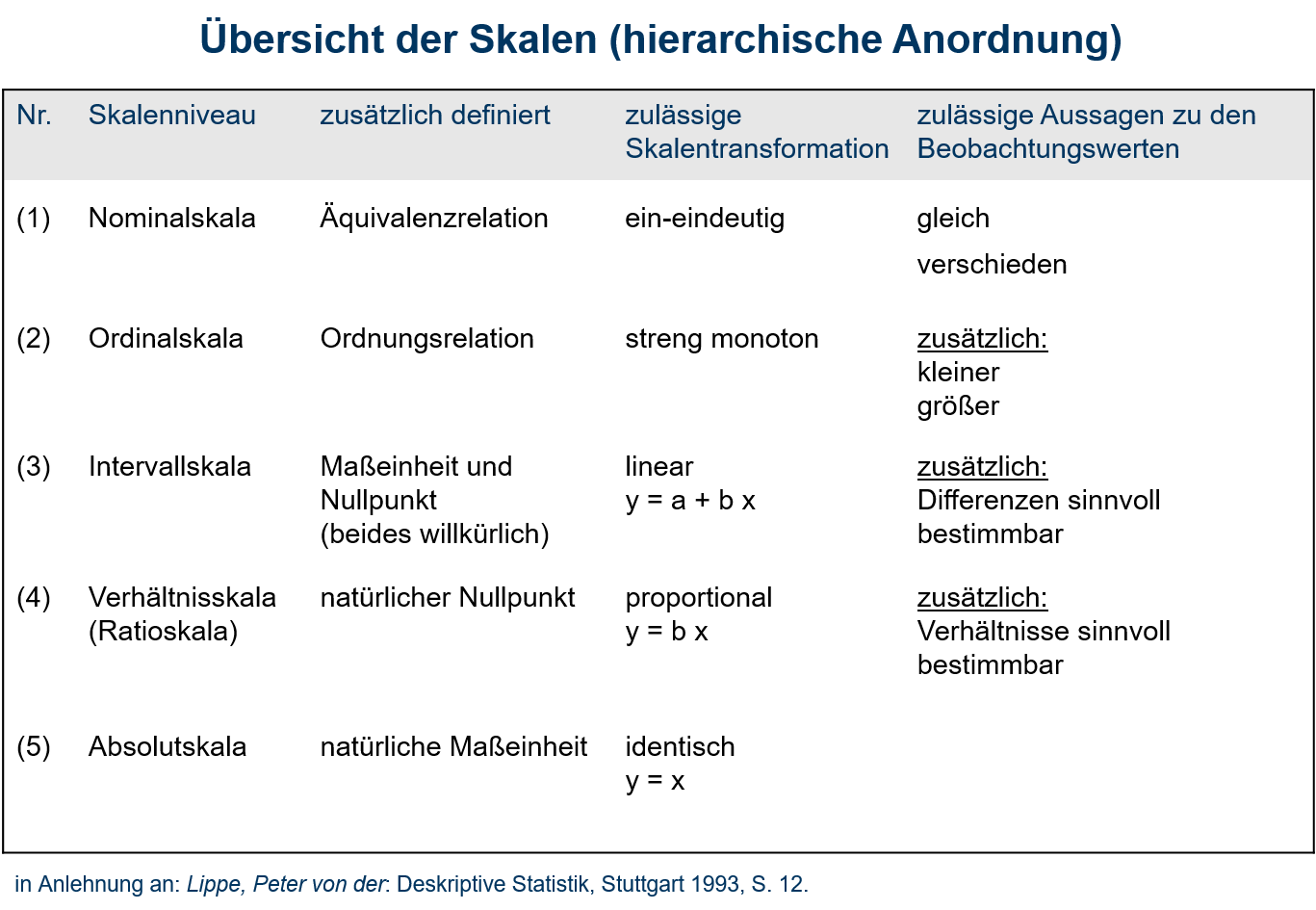
1.3: Transformationen von Skalen