Kapitel 6 Zweidimensionale Datensätze Teil 1
Die Merkmale eines Merkmalsträgers können auch simultan betrachtet werden. Häufig ist von Interesse, ob ein Zusammenhang zwischen den Merkmalen existiert. Im Folgenden werden immer nur zwei Merkmale gleichzeitig betrachtet, welche dann mit \(X\) und \(Y\) bezeichnet werden.
6.1 Kontingenztabellen
Im eindimensionalen Fall, also bei der Betrachtung nur eines Merkmals, konnten die Beobachtungen mit Häufigkeitstabellen übersichtlich dargestellt werden. Auch für zweidimensionale Datensätze existiert die Möglichkeit der Darstellung mit Hilfe spezieller Häufigkeitstabellen, die dann als Kontingenztabellen bezeichnet werden. Tabelle 6.1 zeigt für die Merkmalsträger Verkehrsunfälle in Deutschland mit Personenschäden im Jahr 2016 die erhobenen Merkmale Schweregrad des Unfalls (Merkmal \(X\)) und Ortslage (Merkmal \(Y\)). Zu jedem Merkmal finden sich drei mögliche Ausprägungen und somit resultieren 9 mögliche Kombinationen. Zu jeder Kombination zeigt die Kontingenztabelle die gemeinsame Häufigkeit \(h_{ij}\) auf. Somit bezieht sich \(h_{1 \ 2}=1730\) auf die erste Ausprägung des Merkmals \(X\) und die zweite Ausprägung des Merkmals \(Y\). In der letzten Zeile bzw. letzten Spalte finden sich die Randhäufigkeiten. Diese entsprechen den Häufigkeiten bei eindimensionaler Betrachtung eines Merkmals und resultieren aus der spalten- bzw. zeilenweisen Summation der gemeinsamen Häufigkeiten. Zur Notation sei dabei Folgendes festzuhalten:
- Das Merkmal \(X\) hat \(k\) mögliche Ausprägungen \(a_1, \dots, a_k\)
- Das Merkmal \(Y\) hat \(l\) mögliche Ausprägungen \(b_1, \dots, b_l\)
- \(h(a_i, b_j)=h_{ij}\) ist die gemeinsame absolute Häufigkeit der Merkmalskombination \((a_i, b_j)\)
- Die Randhäufigkeit \(h(a_i)=h_{i.}=\sum_{j=1}^lh_{ij}\) ist die Häufigkeit von \(a_i\)
- Die Randhäufigkeit \(h(b_j)=h_{.j}=\sum_{i=1}^kh_{ij}\) ist die Häufigkeit von \(b_j\)
- \(n=\sum_{i=1}^k \sum_{j=1}^l h_{ij}\) ist die Gesamtzahl der Merkmalsträger
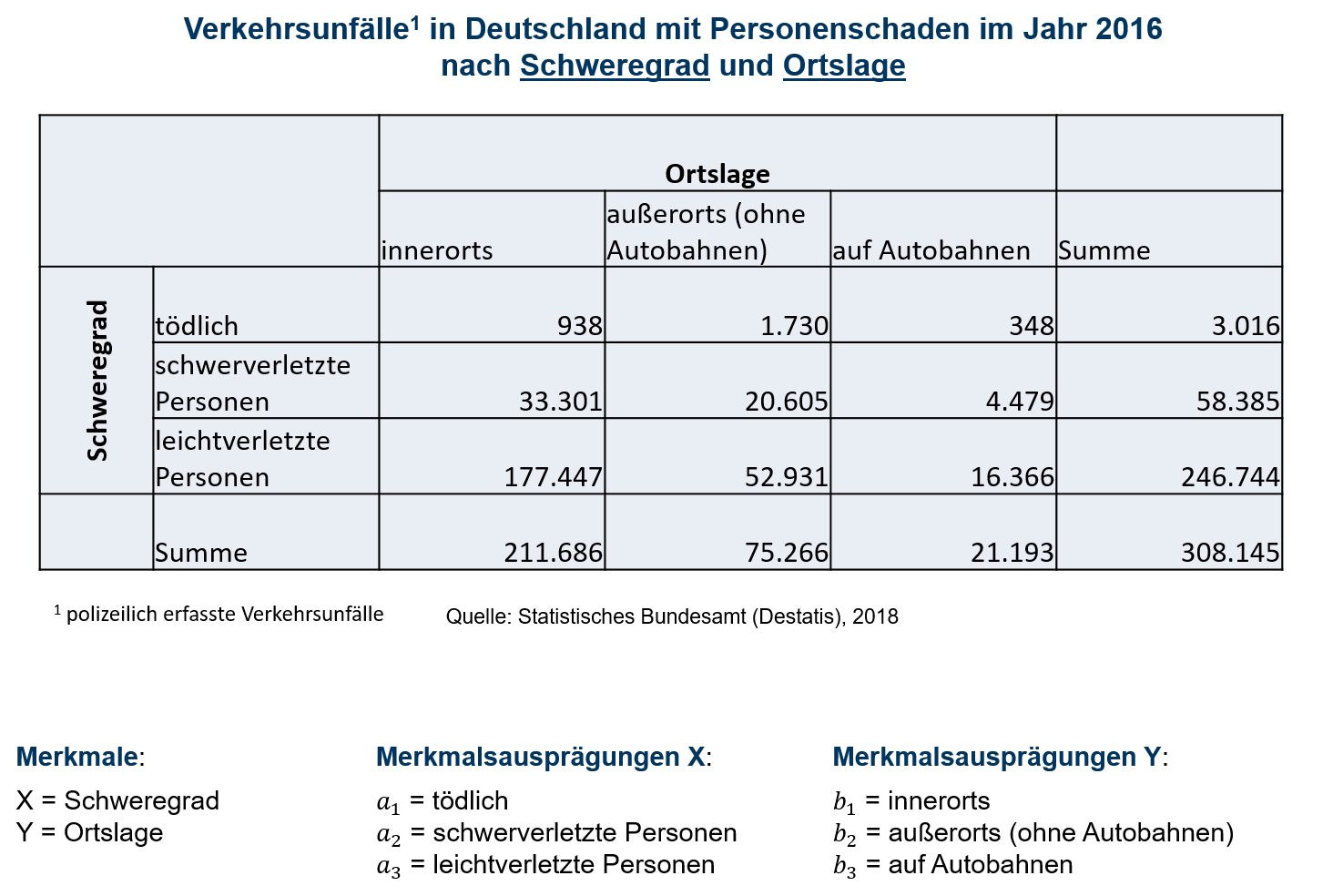
6.1: Kontingenztabelle absolute Häufigkeiten
Im folgenden Videoclip wird nochmal auf die verwendeten Variablenschreibweisen für die Häufigkeiten eingegangen:
Die Kontingenztabelle kann auch zur Darstellung der relativen Häufigkeiten verwendet werden. Dazu werden einfach alle absoluten Häufigkeiten \(h_{ij}\), \(h_{i.}\) und \(h_{.j}\) durch \(n\) dividiert und man erhält \(f(a_i,b_j)\) kurz \(f_{ij}\), \(f(a_i)\) kurz \(f_{i.}\) und \(f(b_j)\) kurz \(f_{.j}\) Tabelle 6.2 zeigt die relativen Häufigkeiten für den betrachteten Datensatz.
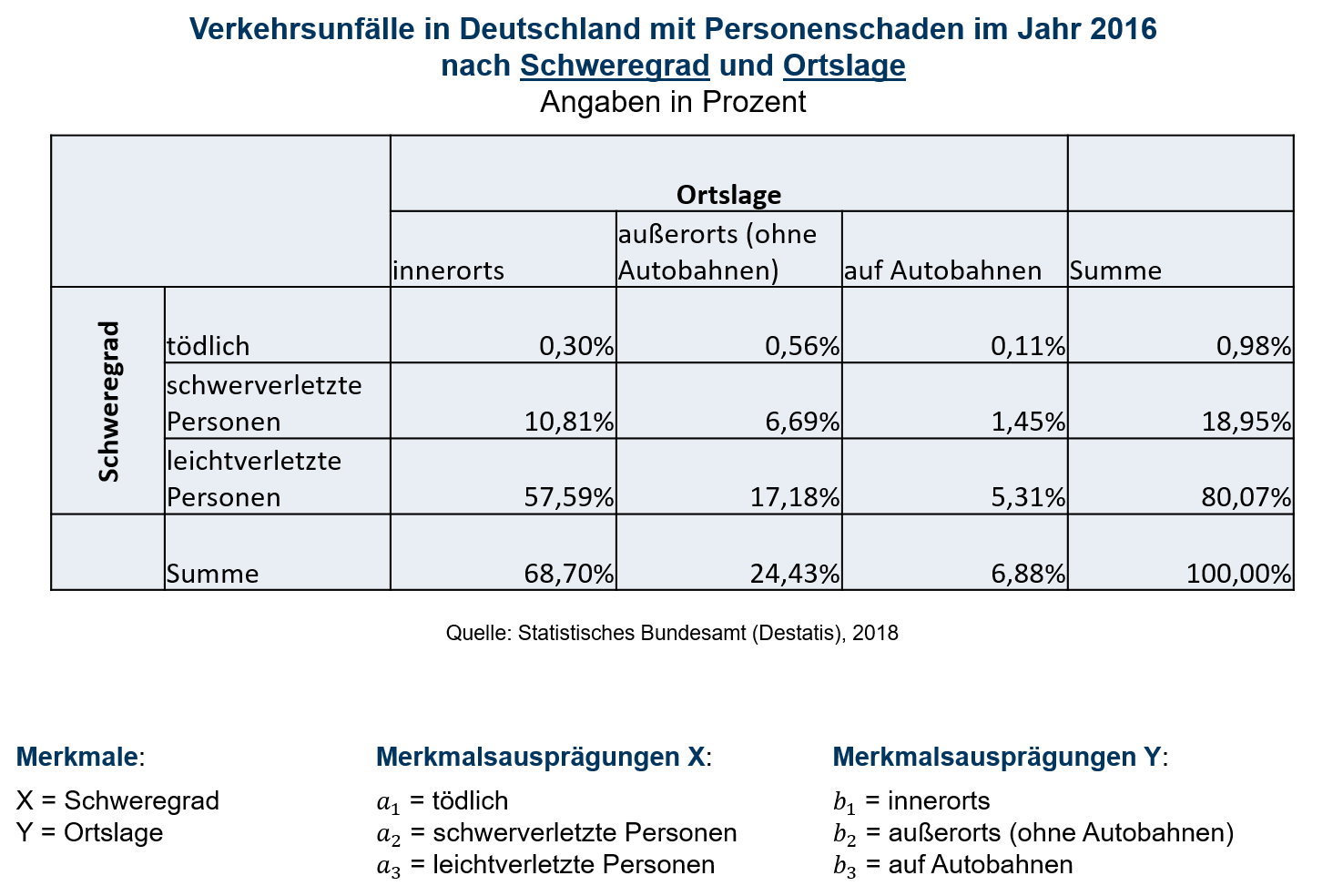
6.2: Kontingenztabelle relative Häufigkeiten
Zunächst einmal lässt sich festhalten, dass Kontingenztabellen sehr gut geeignet sind, wenn die Merkmale jeweils nur wenige mögliche Ausprägungen aufweisen, da andernfalls die Tabelle sehr groß und damit unübersichtlich werden würde. Gerade für qualitative Merkmale, eignen sich Kontingenztabellen somit häufig besonders gut. Es ist jedoch auch möglich, Kontingenztabellen für quantitative Merkmale zu verwenden. Selbst für stetige Merkmale ist deren Einsatz nicht ausgeschlossen. Allerdings würde man in solchen Fällen anstelle einzelner Ausprägungen Klassen betrachten und somit einen Informationsverlust in Kauf nehmen müssen.
6.1.1 bedingte relative Häufigkeiten
Häufig interessiert man sich in Fragestellungen nur für Teile der Grundgesamtheit. Nimmt man etwa nur die Unfälle in den Blick, die außerorts stattgefunden haben und bestimmt für diese den Anteil mit leichtverletzten Personen, so handelt es sich um eine bedingte relative Häufigkeit. Die Bedingung schränkt die Grundgesamtheit ein. Hier ist die Bedingung also Unfälle, die außerorts stattgefunden haben. Konkret wird auf Basis der absoluten Häufigkeiten gerechnet: \[f(a_3|b_2)=\frac{52931}{75266}=0,7033\] oder alternativ auf Basis der relativen Häufigkeiten: \[f(a_3|b_2)=\frac{0,1718}{0,2443}=0,7033\]
allgemein gilt:
\[f(a_i|b_j)=\frac{h_{ij}}{h_{.j}}=\frac{f_{ij}}{f_{.j}} \ \ i \in \{1,...,k\}, \ j \in\{1,...,l\} \] \[f(b_j|a_i)=\frac{h_{ij}}{h_{i.}}=\frac{f_{ij}}{f_{i.}} \ \ i \in \{1,...,k\}, \ j \in\{1,...,l\}\]
Die Bedingung steht immer in der Klammer hinter dem Betragsstrich.
6.1.2 deskriptive Unabhängigkeit
Die Merkmale \(X\) und \(Y\) sind im deskriptiven Sinne unabhängig voneinander, wenn gilt:
\[f(a_i|b_1)=...=f(a_i|b_l)=f(a_i) \ \forall \ i \in \{1,...,k\}\]
Falls dies erfüllt ist, gilt automatisch auch:
\[f(b_j|a_1)=...=f(b_j|a_k)=f(b_j) \ \forall \ j \in \{1,...,l\}\]
und umgekehrt.
Dass die Merkmale Schweregrad und Ortslage voneinander abhängig sind, lässt sich bereits erkennen, wenn man die bereits ermittelte bedingte relative Häufigkeit \(f(a_3|b_2)=0,7033\) und die zugehörige Randhäufigkeit \(f(a_3)=0,8007\) betrachtet, da diese nicht übereinstimmen. Der Anteil an Unfällen mit lediglich leichtverletzten Personen sinkt also, wenn gegenüber der Gesamtheit aller Unfälle nur noch Unfälle betrachtet werden, die sich außerorts ereignet haben. Es steigen dann allerdings die Anteile der Unfälle mit schwerverletzten Personen und tödlichem Ausgang. Nur wenn alle bedingten relativen Häufigkeiten mit den zugehörigen Randhäufigkeiten übereinstimmen, können die Merkmale als im deskriptiven Sinne unabhängig voneinander bezeichnet werden. Tabelle 6.3 zeigt sämtliche bedingten relativen Häufigkeiten \(f(a_i|b_j)\). Hier müssten also zeilenweise alle bedingten relativen Häufigkeiten mit der jeweiligen relativen Randhäufigkeit übereinstimmen, damit man von deskriptiver Unabhängigkeit sprechen kann.
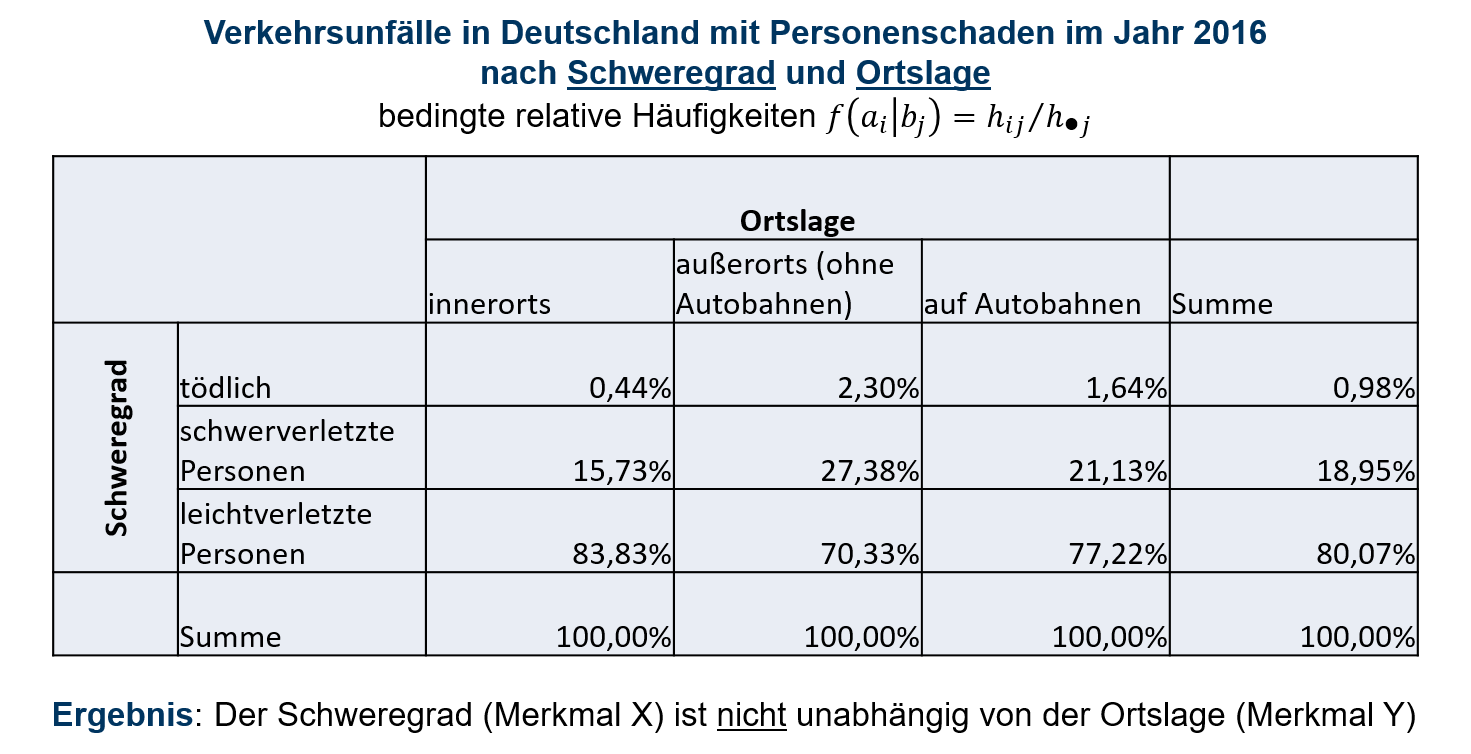
6.3: Kontingenztabelle bedingte relative Häufigkeiten
Im folgenden Videoclip wird erläutert, dass bereits der Vergleich zweier bedingter relativer Häufigkeiten Aufschluss darüber geben kann, ob zwei Merkmale im deskriptiven Sinne abhängig sind:
Außerdem lässt sich festhalten, dass für deskriptiv unabhängige Merkmale gilt:
\[f(a_i)\cdot f(b_j)=f(a_i,b_j) \ \forall \ i \in \{1,..,k\}, j \in \{1,...,l\}\]
denn für deskriptiv unabhängige Merkmale gilt:
\[f(a_i|b_1)=...=f(a_i|b_l)=f(a_i) \ \forall \ i \in \{1,...,k\}\]
Betrachtet man \(f(a_i|b_j)=f(a_i)\) und setzt \(\frac{f(a_i,b_j)}{f(b_j)}\) für \(f(a_i|b_j)\) ein, so resultiert:
\[\begin{align} &\frac{f(a_i,b_j)}{f(b_j)}=f(a_i)\\ \Leftrightarrow&f(a_i,b_j)=f(a_i)\cdot f(b_j) \end{align}\]
Auf Basis von Tabelle 6.2 lässt sich somit auf deskriptive Unabhängigkeit prüfen, indem die gemeinsamen relativen Häufigkeiten mit dem Produkt der zugehörigen relativen Randhäufigkeiten verglichen werden. Beginnt man beispielsweise oben links in der Tabelle, so stellt man wiederum fest, dass die beiden Merkmale abhängig sind, da \[\underbrace{f(a_1)\cdot f(b_1)}_{0,0098\cdot 0,687} \neq \underbrace{f(a_1, b_1)}_{0,003}\]
6.1.3 Kontingenzkoeffizient
Als Maß für den Zusammenhang zwischen zwei Merkmalen kann der Kontingenzkoeffizient nach Pearson bestimmt werden. Den Ausgangspunkt bildet die quadratische Kontingenz \(QK\).
\[QK=\sum_{i=1}^k\sum_{j=1}^l\frac{(h_{ij}-E_{ij})^2}{E_{ij}} \ \mbox{mit} \ E_{ij}=\frac{h_{i.}\cdot h_{.j}}{n}\]
Für deskriptiv unabhängige Merkmale würde dann gelten \(h_{ij}=E_{ij} \ \forall \ (i,j)\) und somit wäre \(QK=0\).
Für die betrachteten Merkmale Personenschaden und Ortslage resultiert: \[QK=\frac{(938-\frac{3016\cdot 211686}{308145})^2}{\frac{3016\cdot 211686}{308145}}+\cdots+\frac{(16366-\frac{246744\cdot 21193}{308145})^2}{\frac{246744\cdot 21193}{308145}}=7373,38 \]
\(QK\) ist jedoch keine normierte Größe und kann mit zunehmender Zahl an Beobachtungen sehr große Werte annehmen. Abhilfe schafft der Kontingenzkoeffizient nach Pearson. Dieser lautet: \[K=\sqrt{\frac{QK}{QK+n}}\] und ist beschränkt auf: \[0\leq K \leq K_{max}=\sqrt{\frac{m-1}{m}} \ \ \mbox{mit} \ \ m=min(k,l)\] Mit \(m\) wird also für beide Merkmale jeweils auf die Zahl der möglichen Ausprägungen geschaut und aus diesen beiden das Minimum gewählt. Um ein Maß zu erhalten, welches auf den Wertebereich von 0 bis 1 normiert ist, betrachtet man einfach \[K^*=\frac{K}{K_{max}}\] \(K^*\) wird als korrigierter Kontingenzkoeffizient bezeichnet. Somit können zweidimensionale Datensätze, hinsichtlich der Stärke des Zusammenhangs ihrer Merkmale miteinander verglichen werden, auch wenn die Datensätze unterschiedliche Anzahlen möglicher Merkmalsausprägungen aufweisen. \(K^*=0\) bedeutet, dass es keinen Zusammenhang zwischen den Merkmalen gibt. Je näher \(K^*\) bei 1 liegt, umso stärker ist der Zusammenhang zwischen den Merkmalen.
Im vorangegangenen Beispiel wurde \(QK=7373,38\) bestimmt.
Es folgt \(K=\sqrt{\frac{7373,38}{7373,38+308145}}=0,1529\).
Da die Merkmale Personenschaden und Ortslage jeweils 3 mögliche Ausprägungen aufweisen, ist \(K_{max}=\sqrt{\frac{3-1}{3}}=0,8165\) und somit \(K^*=\frac{0,1529}{0,8165}=0,1872\).
6.2 Streudiagramme
In einem Streudiagramm werden die Wertepaare \((x_i, y_i)\) als Punkte in einem Koordinatensystem dargestellt. Dazu müssen beide Merkmale quantitativ sein. Durch die Betrachtung von Streudiagrammen lässt sich häufig ein erster Eindruck über den Zusammenhang der Merkmale gewinnen. Streudiagramme sind zur Darstellung zweidimensionaler Datensätze besonders gut geeignet, wenn die Anzahl der \(n\) Wertepaare sehr groß ist und fast alle Wertepaare voneinander verschieden sind.
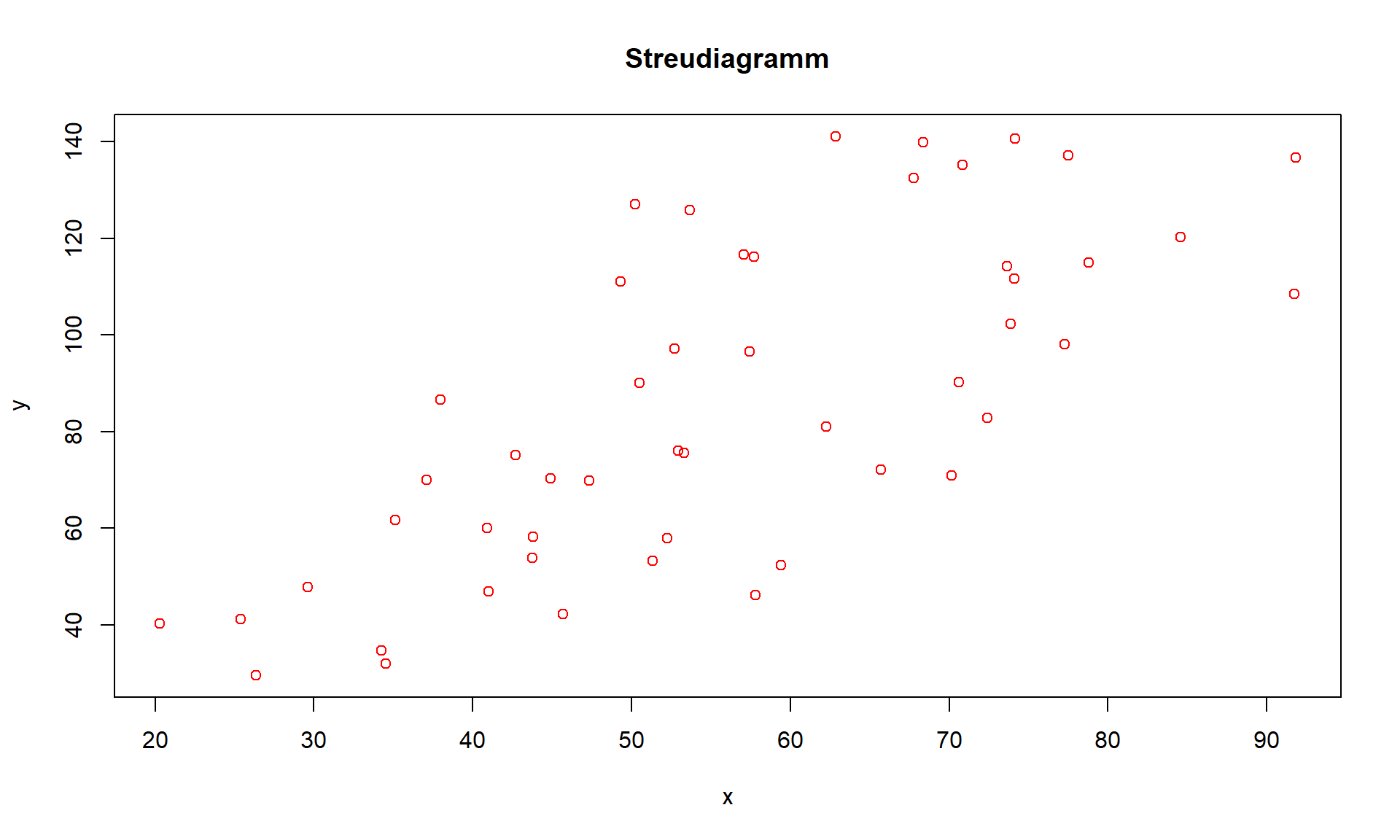
6.4: Streudiagramm
6.3 Korrelation
Die Korrelationsanalyse untersucht Stärke und Richtung des Zusammenhangs von Merkmalen. Ein Zusammenhang kann gleichgerichtet sein, so dass bei metrischen Merkmalen für Merkmalsträger in der Tendenz verhältnismäßig große Werte des einen Merkmals mit verhältnismäßig großen Werten des anderen Merkmals zusammenfallen und verhältnismäßig kleine Werte des einen Merkmals mit verhältnismäßig kleinen Werten des anderen Merkmals zusammenfallen.
Betrachtet man zum Beispiel für Wohngemeinschaften die Merkmale Personenzahl und Wasserverbrauch, so werden tendenziell Wohngemeinschaften, in denen viele Personen leben, einen höheren Wasserverbrauch aufweisen als Wohngemeinschaften, in denen nur wenige Personen leben. In diesem Fall spricht man von einer positiven Korrelation.
Umgekehrt liegt z.B. eine negative Korrelation vor, wenn man für 10 Jahre alte VW Golf die Merkmale Laufleistung in Kilometern und den Gebrauchtwagenwert in € betrachtet.
Im Folgenden werden zur Konzentrationsmessung drei Korrelationskoeffizienten \(r\) vorgestellt.
Allen Korrelationskoeffizienten ist gemein, dass sie auf einen Wertebereich von \(r \in [-1,+1]\) normiert sind.
Das Vorzeichen entscheidet über die Richtung des Zusammenhangs:
| \(r>0\): | positive Korrelation |
| \(r<0\): | negative Korrelation |
Der Absolutbetrag gibt die Stärke des Zusammenhangs an.
Es gelten die folgenden Faustformeln:
| \(0,8<|r|\): | starke Korrelation |
| \(0,5<|r|\leq0,8\): | mittlere Korrelation |
| \(0,3<|r|\leq0,5\): | schwache Korrelation |
| \(|r|\leq0,3\): | keine Korrelation |
6.3.1 \(r_F\) von Fechner
Der Korrelationskoeffizient nach Fechner lautet:
\[\begin{align} r_F=\frac{\ddot{U}-N}{\ddot{U}+N} \end{align}\]
Dabei steht \(\ddot{U}\) für die Anzahl der Übereinstimmungen in den Vorzeichen der \(n\) Wertepaare \[(x_i-\overline{x}, \ y_i-\overline{y})\] und \(N\) für die Anzahl der Nichtübereinstimmungen in den Vorzeichen. Somit kann \(N\) auch aus \(N=n-\ddot{U}\) bestimmt werden. Für jeden Merkmalsträger \(i\) ist also zu schauen, ob ein über-oder unterdurchschnittlicher Wert \(x_i\) vorliegt und ob dieser mit einem über-oder unterdurchschnittlichen Wert \(y_i\) zusammenfällt. Sind \(x_i\) und \(y_i\) für einen Merkmalsträger \(i\) beide überdurchschnittlich oder beide unterdurchschnittlich, so wird dies als Übereinstimmung in den Vorzeichen gewertet. Sollte ein Wert \(x_i\) bzw. ein Wert \(y_i\) genau mit dem arithmetischen Mittel des betrachteten Merkmals übereinstimmen, man spricht dann auch von einer Bindung, so wird dies immer als Übereinstimmung in den Vorzeichen gewertet, egal welches Vorzeichen bei der Betrachtung des zweiten Merkmals vorliegt.
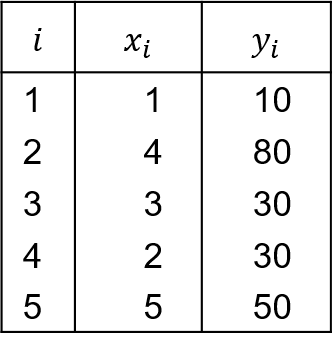
6.5: Zahlenbeispiel
Im Beispiel aus Tabelle 6.5 werden für 5 Dienstleistungsunternehmen einer Branche deren Mitarbeiterzahl (Merkmal \(X\)) und der monatliche Umsatz in Tsd. Euro (Merkmal \(Y\)) betrachtet. Es folgen \(\overline{x}=40\) und \(\overline{y}=3\) und es resultiert
\[\begin{align} r_F=\frac{5-0}{5+0}=1 \end{align}\]
Es liegt somit für die fünf Unternehmen der Branche eine starke positive Korrelation zwischen dem Umsatz und der Mitarbeiterzahl vor.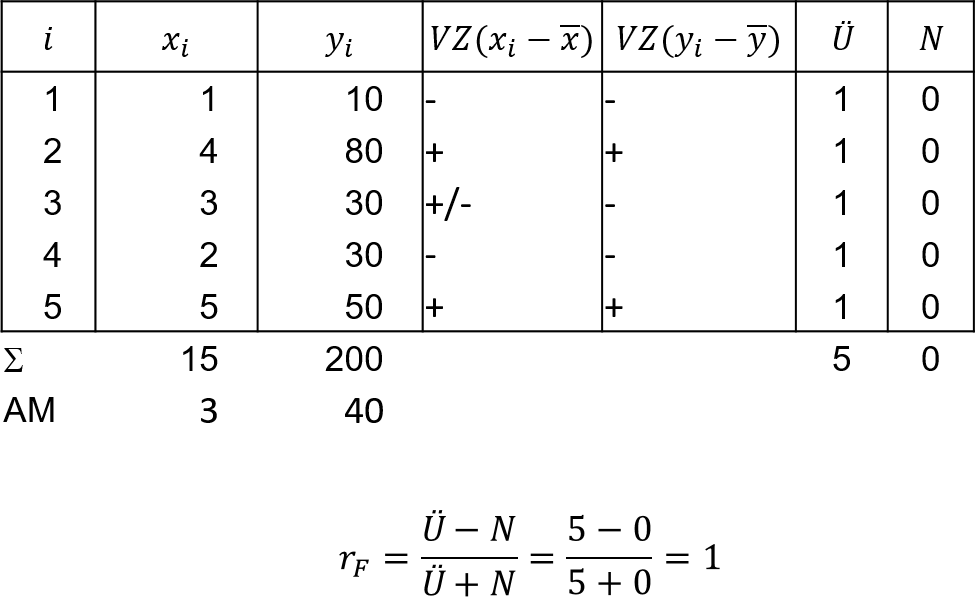
6.6: Korrelationskoeffizient nach Fechner
Die Anzahl der Übereinstimmungen und nicht Übereinstimmungen in den Vorzeichen kann unter Angabe der arithmetischen Mittel einfach aus dem folgenden Streudiagramm abgelesen werden. So stehen die Quadranten oben rechts und unten links jeweils für eine Übereinstimmung in den Vorzeichen, da hier die X- und Y-Werte beide überdurchschnittlich (oben rechts) bzw. beide unterdurchschnittlich (unten links) sind. Der Punkt auf der Vertikalen stimmt mit seiner X-Koordinate mit \(\overline{x}\) überein. Wie vereinbart, wird dies als Übereinstimmung in den Vorzeichen der beiden Abweichungen interpretiert und der Punkt somit dem Quadranten unten links zugeordnet.
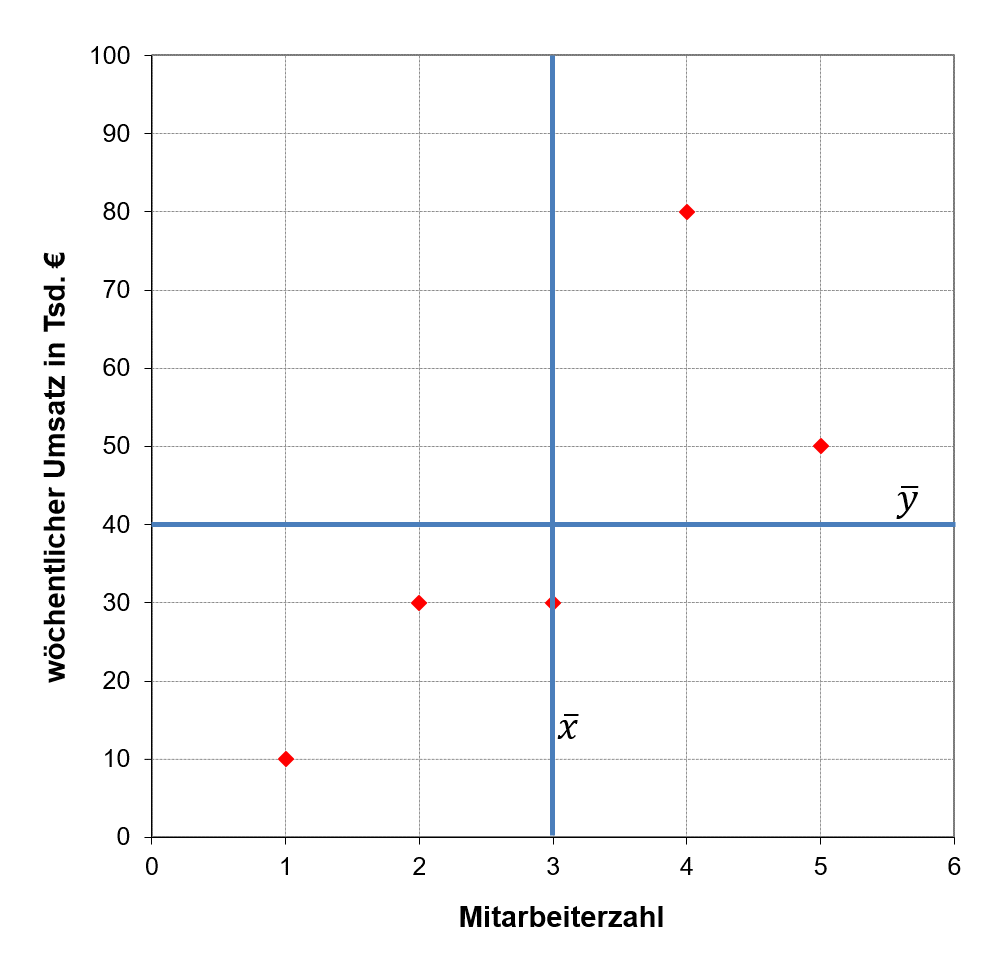
6.7: Streudiagramm und Korrelationskoeffizient nach Fechner
6.3.2 \(r_{BP}\) von Bravais-Pearson
Der Korrelationskoeffizient nach Bravais-Pearson lautet:
\[\begin{align} r_{BP}=\frac{S_{xy}}{S_xS_y}=\frac{\sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum_{i=1}^n (x_i-\overline{x})^2}\sqrt{\sum_{i=1}^n (y_i-\overline{y})^2}} \end{align}\]
Dabei bezeichnet \(S_{xy}\) die Kovarianz der beiden Merkmale \(X\) und \(Y\) und \(S_x\) bzw.\(S_y\) sind die beiden Standardabweichungen.
Die Kovarianz \(S_{xy}\) ist ein nichtstandardisiertes Maß für den Zusammenhang, deren Vorzeichen über die Richtung des Zusammenhangs entscheidet. Wie schon beim Korrelationskoeffizient nach Fechner werden die Abweichungen \((x_i-\overline{x}, \ y_i-\overline{y})\) betrachtet. Jedoch fließen in die Berechnung von \(r_{BP}\) mehr Informationen als in \(r_F\) ein, da für \(r_{BP}\) nicht nur das Vorzeichen der Abweichungen berücksichtigt wird.
Erst durch die Division durch \(S_xS_y\) erhält man mit \(r_{BP}\) ein normiertes Maß, für das gilt: \(r_{BP} \in [-1,+1]\).
Beide Merkmale müssen für die Berechnung von \(r_{BP}\) mindestens intervallskaliert sein.
Abbildung 6.8 zeigt die Berechnung von \(r_{BP}\) für das Zahlenbeispiel 6.5.
6.8: Korrelationskoeffizient nach Bravais-Pearson
\(|r_{BP}|=1\) gilt nur dann, wenn alle Punkte auf einer Geraden liegen, also \[y_i=a+bx_i \ \ \mbox{mit} \ \ b \neq 0 \]
Die folgenden Abbildungen zeigen Beispiele für positive, negative und nicht vorhandene Korrelation auf:
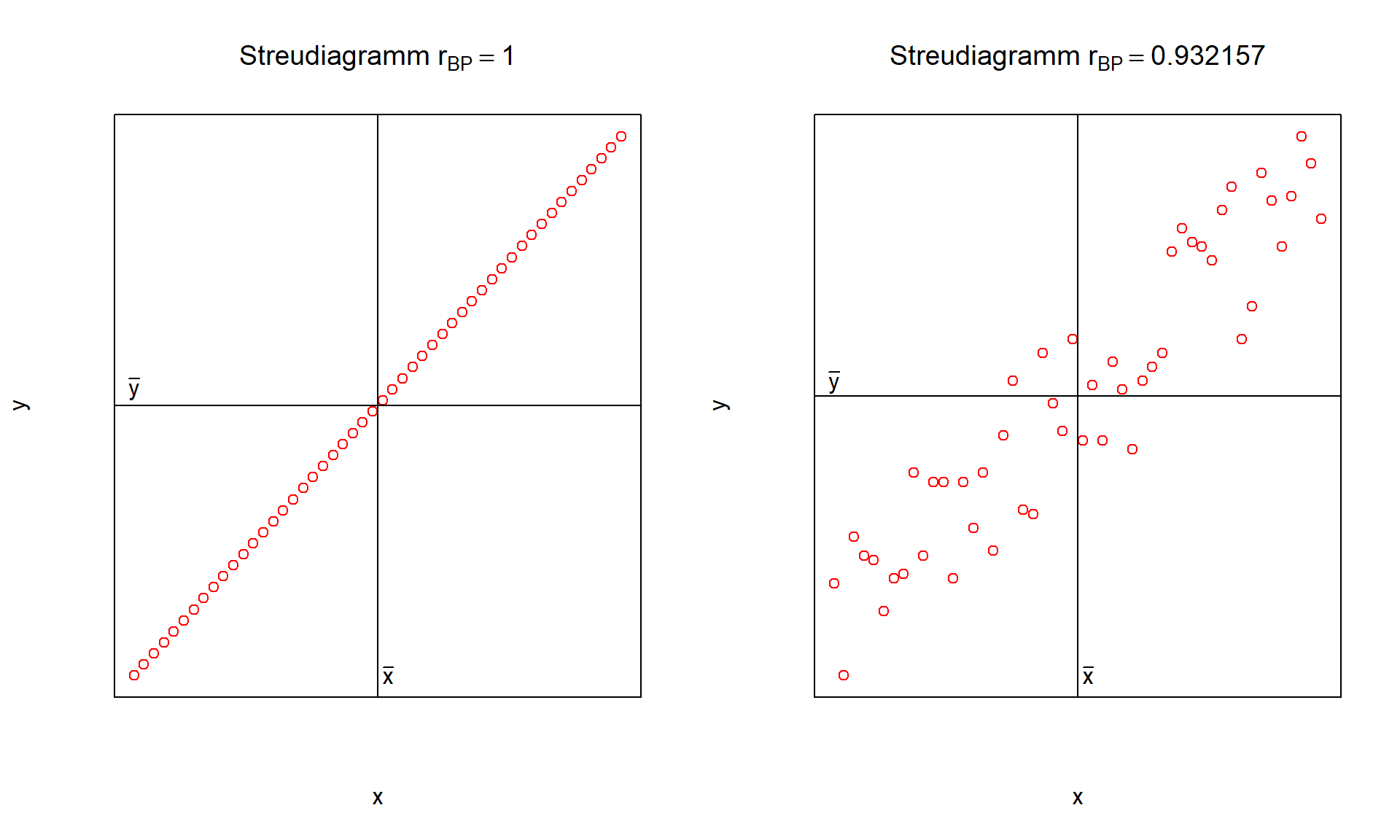
6.9: positive Korrelation
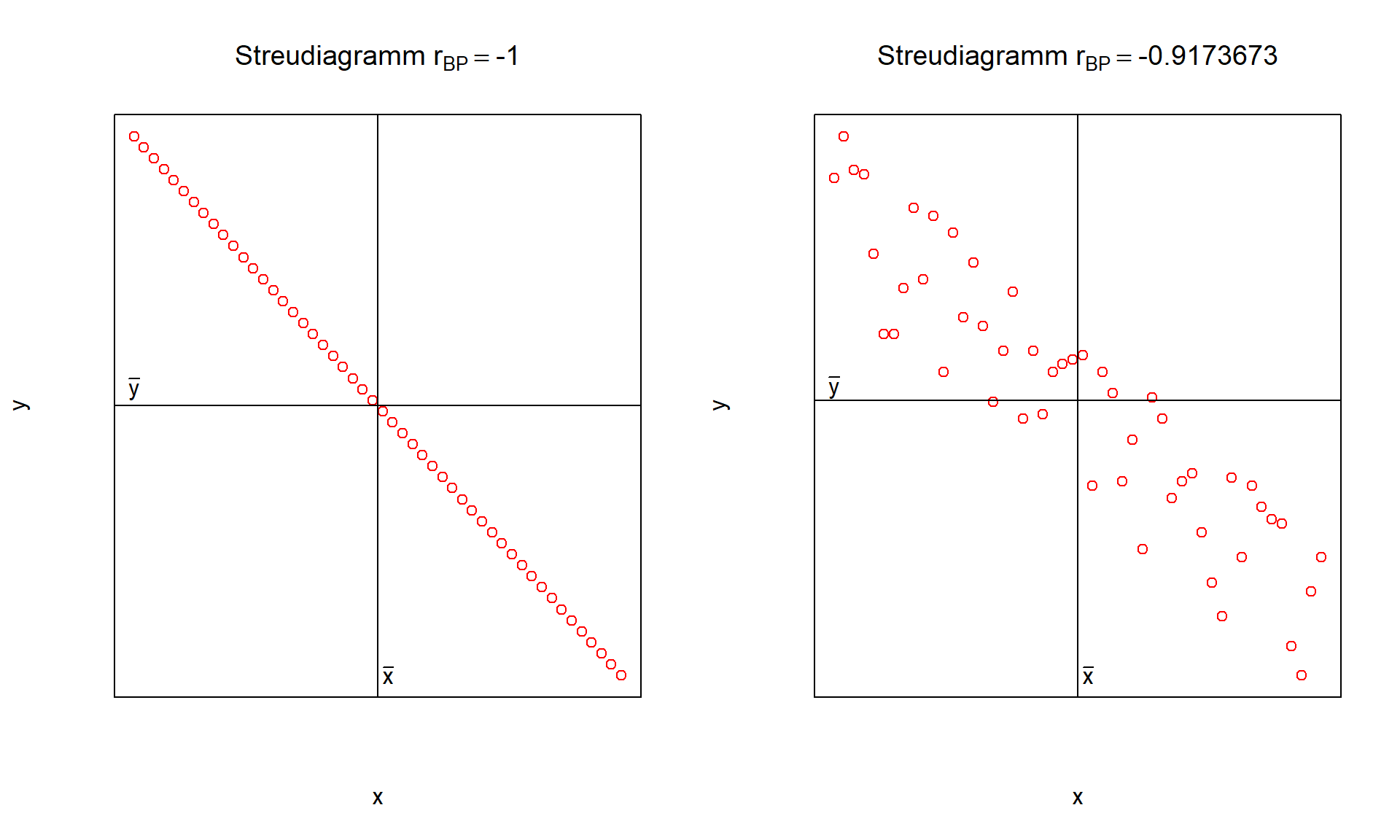
6.10: negative Korrelation
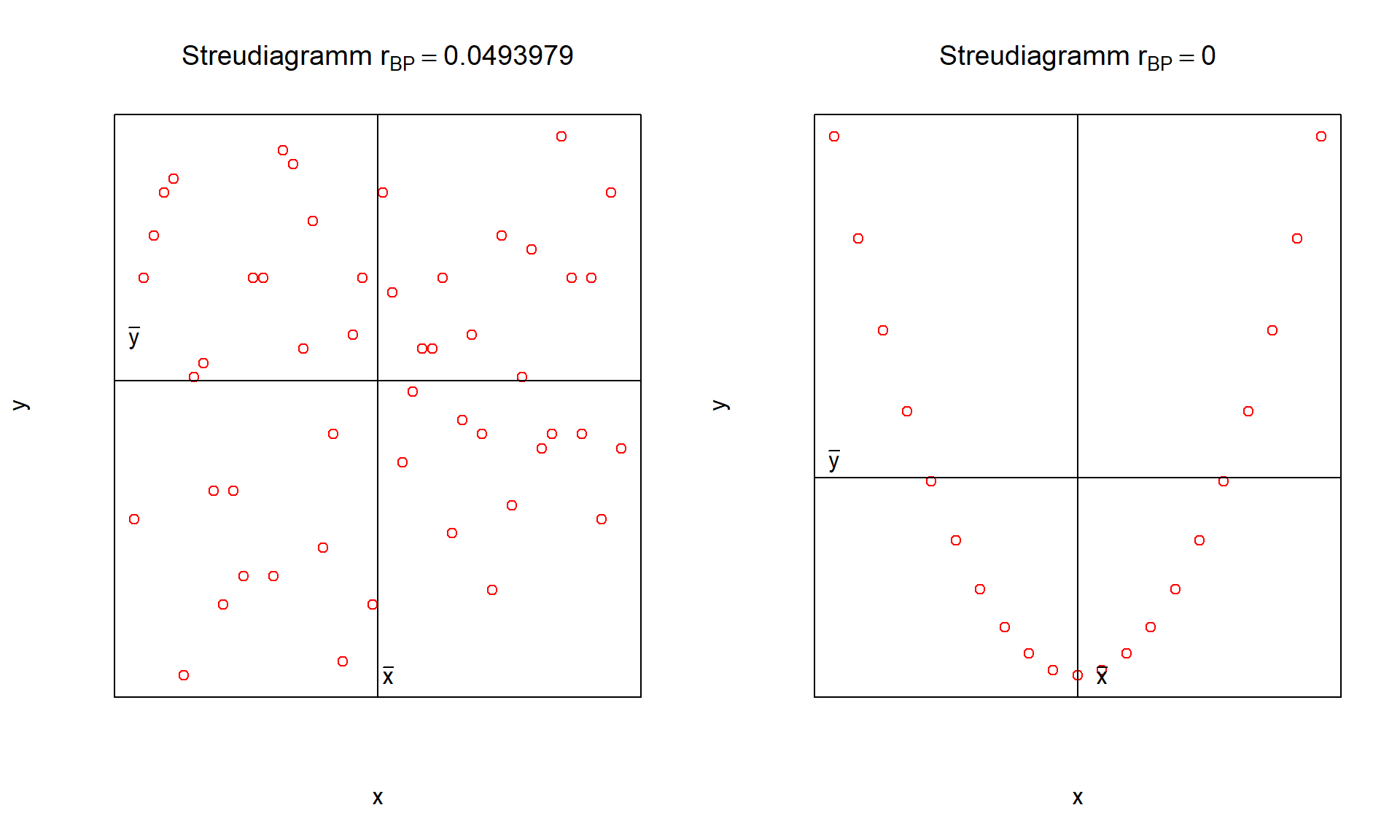
6.11: keine Korrelation
Aus dem rechten Streudiagramm in Abbildung 6.11 geht deutlich hervor, dass die Merkmale \(X\) und \(Y\) abhängig sind. Hier liegt ein Zusammenhang der Form \(y=x^2\) vor. Es liegt allerdings keine Korrelation vor, da der Zusammenhang nicht gleichgerichtet und auch nicht entgegengerichtet ist. Es ist also möglich, dass zwei Merkmale abhängig sind, obwohl sie unkorreliert sind. Sind zwei Merkmale jedoch unabhängig, so liegt keinerlei Zusammenhang und somit auch keine Korrelation vor.
6.3.3 \(r_{SP}\) von Spearman (Rangkorrelationskoeffizient)
Der Korrelationskoeffizient nach Spearman \(r_{SP}\) kann bereits ab Ordinalskalenniveau bestimmt werden. \(r_{SP}\) basiert auf der Formel des Korrelationskoeffizienten nach Bravais-Pearson, jedoch werden nicht die Beobachtungen selber, sondern deren Rangzahlen zur Berechnung herangezogen. D.h., den Beobachtungen werden Ränge \(R(x_i)\) in Form von natürlichen Zahlen zugewiesen, mit denen anschließend gerechnet werden kann. \[r_{Sp}=\frac{\sum_{i=1}^n(R(x_i)-\frac{n+1}{2})(R(y_i)-\frac{n+1}{2})}{\sqrt{ \sum_{i=1}^n (R(x_i)-\frac{n+1}{2})^2\sum_{i=1}^n (R(y_i)-\frac{n+1}{2})^2}} \ \ \mbox{wobei} \ \ \overline{R}(x_i)=\overline{R}(y_i)=\frac{n+1}{2}\] Zu unterscheiden ist, ob Bindungen oder keine Bindungen vorliegen. Bindungen bezeichnen das mehrfache Auftreten derselben Beobachtungswerte eines Merkmals.
falls keine Bindungen vorliegen
Nachdem den Beobachtungen jedes Merkmals die natürlichen Zahlen von \(1\) bis \(n\) als Rangzahlen eindeutig zugeordnet werden konnten, erfolgt die Berechnung von \(r_{SP}\). Anstelle von \(r_{SP}\) kann dann auch folgende Formel verwendet werden: \[r_{SP}^*=1-\frac{6\cdot\sum_{i=1}^n d_i^2}{n(n^2-1)} \ \ \mbox{mit} \ \ d_i=R(x_i)-R(y_i)\] \(r_{SP}\) kann in \(r_{SP}^*\) überführt werden, falls keine Bindungen vorliegen. Sofern Bindungen vorliegen liefert \(r_{SP}^*\) lediglich eine Näherungslösung und sollte nicht verwendet werden.
Tabelle 6.12 zeigt für 4 Schülerinnen und Schüler die Mathenote und die Englischnote. Die zugehörigen Rangzahlen finden sich in den beiden letzten Spalten. Zwischen der Mathenote und der Englischnote liegt für die 4 Schülerinnen und Schüler keine Korrelation vor, \(r_{SP}^*=0\).
6.12: Beispiel Noten 1
Die einzelnen Rechenschritte können im folgenden Video nachvollzogen werden:
falls Bindungen vorliegen
Beim Vorliegen von Bindungen werden den Beobachtungen zunächst wieder Rangzahlen entsprechend ihrer Position in der geordneten Urliste zugewiesen. Beobachtungen, die mehrfach auftreten, können jedoch keine eindeutigen Rangzahlen erhalten. Um eine willkürliche Vergabe zu vermeiden erhalten diese Beobachtungen den Durchschnittswert der auf sie entfallenen Rangzahlen. Der Durchschnitt der Rangzahlen lautet somit für beide Merkmale nach wie vor \(\overline{R}(x_i)=\overline{R}(y_i)=\frac{n+1}{2}\) und \(r_{SP}\) kann verwendet werden.
Tabelle 6.13 zeigt für 7 Schülerinnen und Schüler die Mathenote und die Englischnote. Zwischen der Mathenote und der Englischnote liegt für die 7 Schülerinnen und Schüler eine schwache negative Korrelation vor, \(r_{SP}^*=-0,3981\).
6.13: Beispiel Noten 2
Im folgenden Video wird der Korrelationskoeffizient \(r_{SP}\) für das Zahlenbeispiel aus Tabelle 6.13 ermittelt:
Der Rechenweg kann zudem in Abbildung 6.14 nachfollzogen werden.
6.14: Korrelationskoeffizient nach Spearman mit Bindungen
6.3.4 mögliche Probleme
nichtlineare Zusammenhänge Zusammenhänge, die nicht linear sind, werden häufig durch die Korrelationsanalyse unzureichend abgebildet.
Problem der Kausalität: Die Korrelationsanalyse lässt keinen Rückschluss auf eine kausale Beziehung zwischen den Merkmalen zu. Am Korrelationskoeffizienten kann man nicht erkennen, ob \(X\) die Ursache für \(Y\) oder \(Y\) die Ursache für \(X\) ist.
Problem der Scheinkorrelation aufgrund von dritten Variablen: \(X\) und \(Y\) korrelieren nur deshalb miteinander, weil sie gemeinsam von einer dritten Variablen \(Z\) abhängig sind. Betrachtet man beispielsweise für verschiedene Regionen in Deutschland die Dichte an Störchen und die Geburtenraten der Bevölkerungen, so stellt man eine positive Korrelation fest. Dieses begründet sich aber im Urbanisierungsgrad der Regionen. Klassische, kinderreiche Familienbilder sind häufiger im ländlichen Bereich zu finden, wo auch Störche bessere Lebensbedingungen vorfinden.
Problem der Scheinkorrelation bei Zeitreihendaten: Der Korrelationskoeffizient signalisiert einen Zusammenhang, für den es keine inhaltliche Erklärung gibt. Dieses Phänomen tritt häufig in Verbindung mit trendbehafteten Zeitreihendaten auf.
Problem der Zufallskorrelation: Die Grundgesamtheit bzw. Stichprobe ist zu klein, um eine sinnvolle Korrelationsanalyse durchführen zu können.