Kapitel 7 Zweidimensionale Datensätze Teil 2

7.1 Regressionsanalyse

Mit der Korrelationsanalyse wurde betrachtet, ob ein gleich- oder entgegengerichteter Zusammenhang zwischen zwei Merkmalen vorliegt, ohne dass der Korrelationskoeffizient dabei Auskunft über die Kausalität (Ursache-Wirkungsbeziehung) gibt. Im Rahmen der Regressionsanalyse ist genau festzulegen, welches das abhängige Merkmal, im Folgenden mit \(y\) bezeichnet, und welches das erklärende (unabhängige) Merkmal, im Folgenden mit \(x\) bezeichnet, ist. \(y\) ist somit eine Funktion von \(x\). Wir beschränken uns dabei auf lineare Abhängigkeiten der Form \[y=a+b\cdot x\] Tabelle 7.1 zeigt für einen Händler von Edelfischen an 10 unterschiedlichen Verkaufstagen den vom Händler festgelegten Preis in € pro kg (\(x\)) und die nachgefragte Menge in kg (\(y\)). In das zugehörige Streudiagramm in Abbildung 7.2 wurde die Regressionsgerade \(y=a+b\cdot x\) eingezeichnet, mit der Zielsetzung, die abgesetzte Menge durch den gewählten Verkaufspreis zu erklären. Es ist deutlich zu erkennen, dass die eingezeichnete Gerade nicht durch alle Punkte verläuft, es also keine perfekt lineare Beziehung zwischen \(y\) und \(x\) gibt, wie dies der Fall wäre, bei einem Korrelationskoeffizienten nach Bravais-Pearson von \(r_{BP}=1\) bzw. \(r_{BP}=-1\).

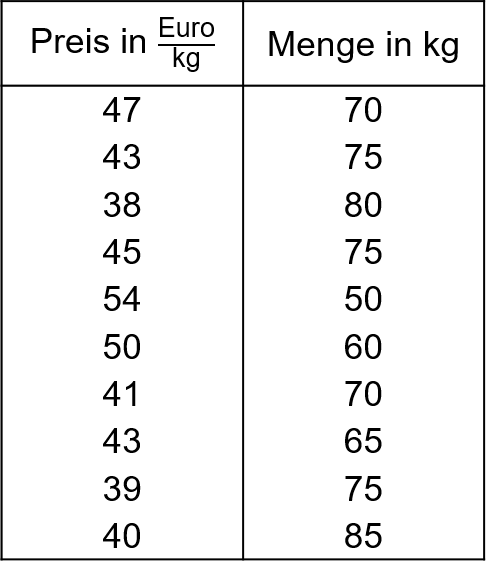
7.1: Beispiel Fischhändler

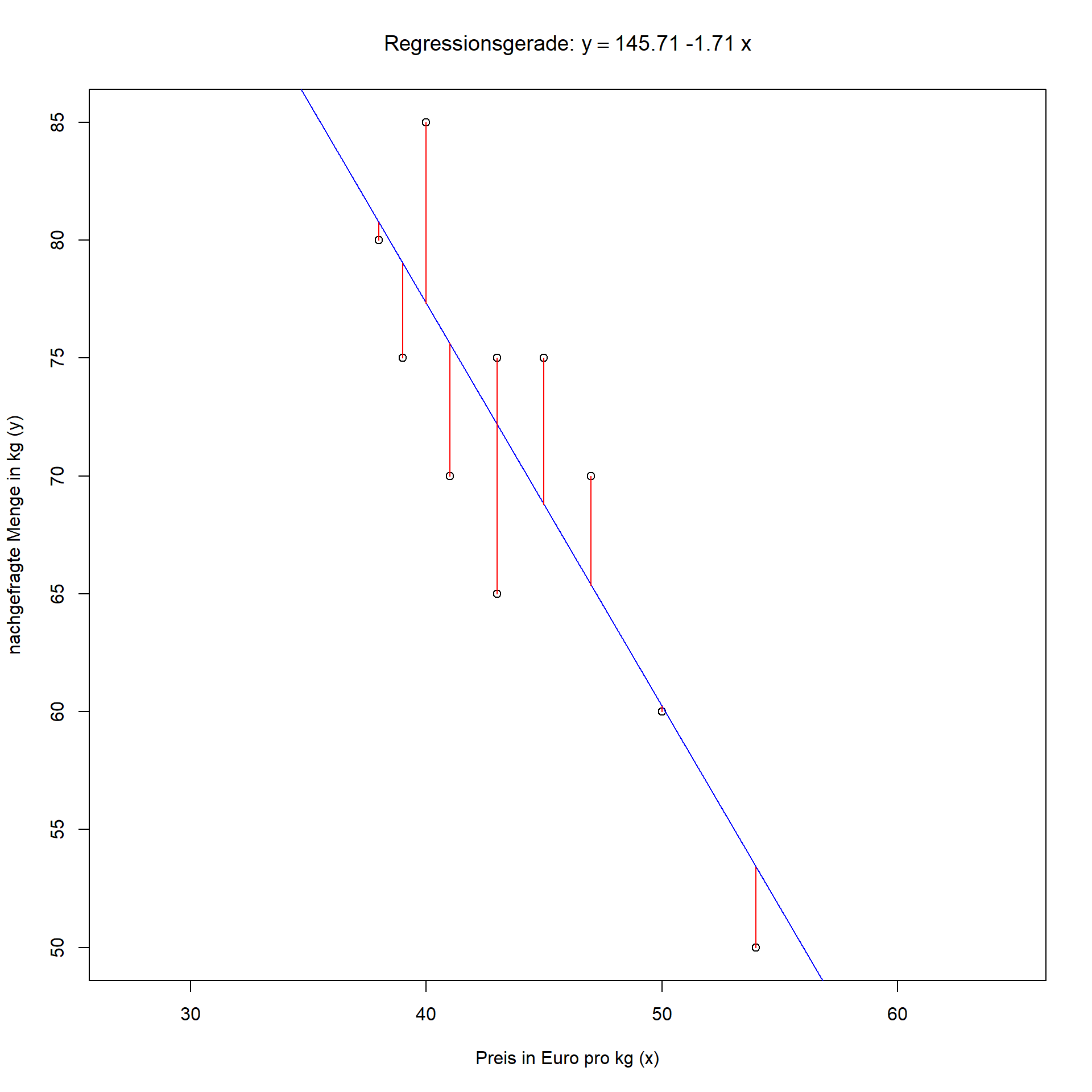
7.2: Regressionsgerade

Die lineare Beziehung von \(y\) und \(x\) wird also überlagert von Abweichungen,die nicht näher erklärt werden können und auch als Residuen bezeichnet werden. Für die Residuen, als senkrechte Abweichungen zwischen den Punkte \((x_i,y_i)\) und der Geraden, wird die Variablenbezeichnung \(u_i\) verwendet. Es gilt somit: \[y_i=a+b\cdot x_i+u_i\]

Bestimmung der Koeffizienten

Die Methode der Kleinsten Quadrate zur Bestimmung der Koeffizienten wird im Folgenden und unterstützend in diesem Videoclip erläutert:

Nun stellt sich die Frage, wie die Gerade am besten der Punktwolke angepasst werden soll. Dazu wählen wir die Methode der Kleinsten Quadrate. Wie in Abbildung 7.3 durch die Quadrate zu jeder Abweichung dargestellt, werden die Koeffizienten \(a\) und \(b\) der Regressionsgeraden so gewählt, dass die Summe der quadratischen Abweichungen, also \(\sum_{i=1}^n u_i^2\) minimal ausfällt. Mit dieser Zielsetzung erhält man eine eindeutige Lösung für die gilt, dass der größtmögliche Anteil der Variation in der abhängigen Variablen \(y\) durch das Modell erklärt werden kann.
Formal wird die Summe der quadrierten Residuen als Funktion der Variablen \(a\) und \(b\) notiert und im Folgenden mit: \[Q(a,b)=\sum_{i=1}^n u_i^2=\sum_{i=1}^n\left(y_i-(a+bx_i)\right)^2\] bezeichnet, für welche die Minimierungsaufgabe \(\underset{a,b}{min}\left(Q(a,b)\right)\) zu lösen ist.
Dazu werden die partiellen Ableitungen nach \(a\) und \(b\) bestimmt und jeweils mit Null gleichgesetzt.
Schließlich können aus den beiden resultierenden Gleichungen durch Umstellen und Einsetzen die folgenden Berechnungsvorschriften für \(a\) und \(b\) bestimmt werden (zur Herleitung):

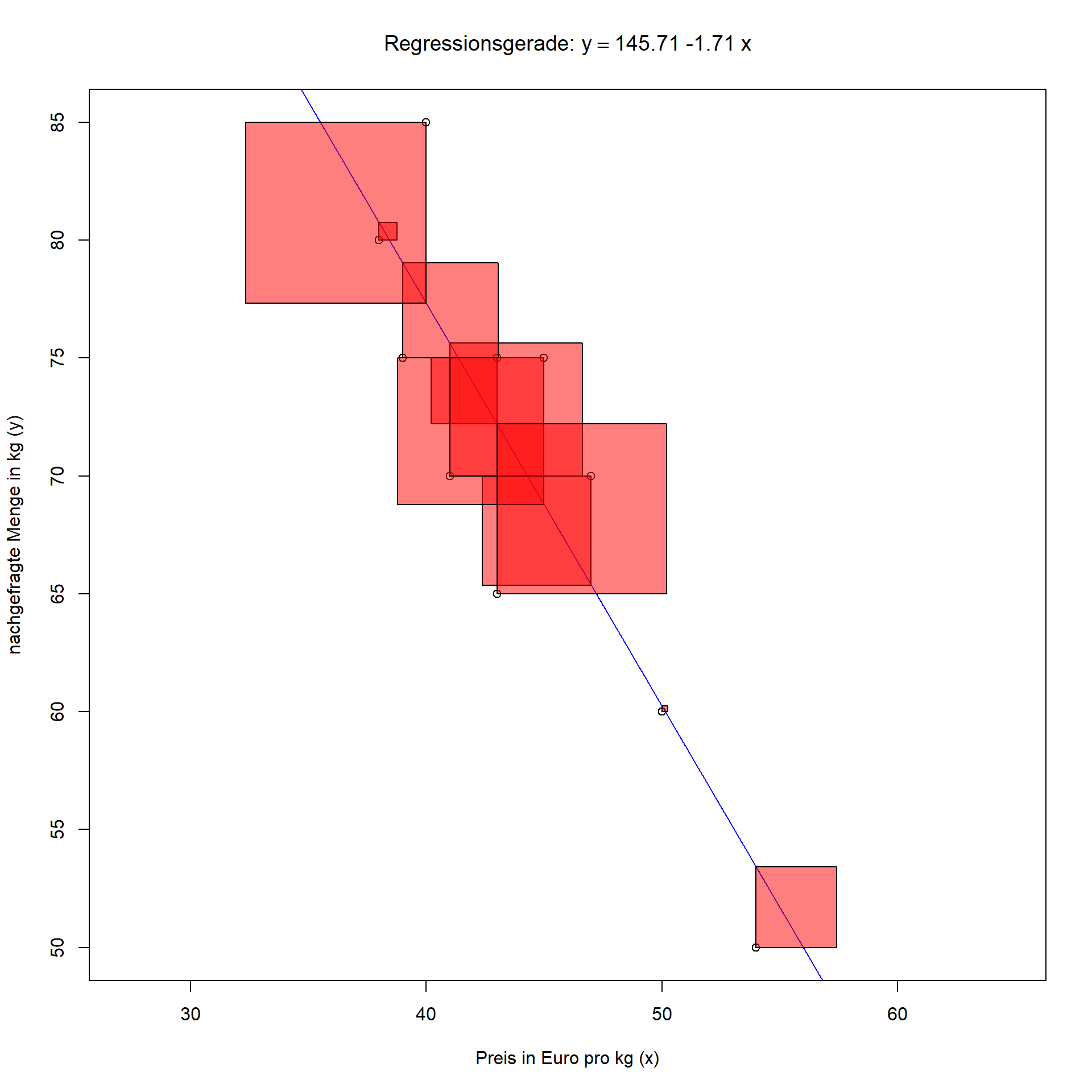
7.3: Regressionsgerade mit quadratischen Abweichungen

\[\begin{align} & 1) \ \ b=\frac{\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sum_{i=1}^n(x_i-\overline{x})^2}=\frac{S_{xy}}{S_x^2}\\ & \\ & 2) \ \ a=\overline{y}-b\overline{x} \end{align}\]

Eine Lösung existiert nur dann, sofern eine Variation für das Merkmal \(x\) vorliegt, also der Nenner aus 1) größer Null ist.
Im Beispiel des Fischhändlers lautet die Regressionsgerade: \[y=145,71-1,71\cdot x\]

Die einzelnen Rechenschritte sind in Abbildung 7.4 dargestellt.

7.4: Beispiel Fischhändler Berechnung der Koeffizienten

Interpretation der Koeffizienten

Der Koeffizient \(b\) besagt somit, dass jede Erhöhung des Preises um einen Euro pro kg im Durchschnitt mit einem Rückgang der nachgefragten Menge um 1,71 kg einhergeht.
Für einen \(x\) Wert von Null (Preis von 0€) entspricht \(y\) (die nachgefragte Menge) dem Koeffizienten \(a\). Hier ist jedoch Vorsicht bei der Interpretation geboten. Die lineare Beziehung zwischen zwei Merkmalen kann in vielen Fällen, wenn überhaupt, nur für einen gewissen Wertebereich sinnvoll unterstellt werden. Wenn man für die erklärende Variable das Intervall der Beobachtungswerte weit verlässt, so gilt die lineare Abhängigkeit häufig nicht mehr. Man sollte also nicht davon ausgehen, dass der Fischhändler 145,71 kg absetzen würde, falls er seinen Fisch verschenkt.

Prognosen

Die Werte für \(y\), welche sich aus der Vorschrift \(\widehat{y}=a+b\cdot x\) ergeben und somit genau auf der Regressionsgeraden liegen, werden theoretische y-Werte genannt und mit \(\widehat{y}\) bezeichnet. Zu jedem \(x_i\) aus dem Paar der Beobachtungswerte \((x_i,y_i)\) lässt sich somit auch ein theoretischer Wert \(\widehat{y}_i\) angeben. Zudem können natürlich auch für Ausprägungen von \(x\), zu denen keine Beobachtungen vorliegen, theoretische y-Werte bestimmt werden. So kann z.B. für einen Preis von 42 € pro kg die abgesetzte Menge prognostiziert werden: \[\widehat{y}=145,71-1,71\cdot 42=73,89\]

Varianzzerlegung

Die Gesamtvarianz der abhängigen Variablen \(y\) lässt sich in die beiden folgenden Varianzen zerlegen: \[\underset{\mbox{Gesamtvarianz}}{\frac{1}{n}\sum_{i=1}^n(y_i-\overline{y})^2}=\underset{\mbox{erklärte Varianz}}{\frac{1}{n}\sum_{i=1}^n(\hat{y}_i-\overline{y})^2} \ \ \ \ \ \ +\underset{\mbox{nicht erklärte Varianz}}{\frac{1}{n}\sum_{i=1}^nu_i^2}\]

Folgende Eigenschaften führen zu der oben dargestellten Varianzzerlegung:

• \(u_i=y_i-\hat{y}_i\) sind die Residuen, welche aus der Differenz der beobachteten Werte \(y_i\) und der theoretischen Werte \(\hat{y}_i\) ermittelt werden.
• Es gilt: \(\sum_{i=1}^nu_i=0\).
• Außerdem gilt: \(\sum_{i=1}^n\hat{y}_iu_i=0\)
• Für die theoretischen y-Werte \(\hat{y}_i\) gilt: \(\overline{\hat{y}}=\overline{y}\)

Determinationskoeffizient

Das Verhältnis aus erklärter Varianz zur Gesamtvarianz, also \[d=\frac{\frac{1}{n}\sum_{i=1}^n(\hat{y}_i-\overline{y})^2}{\frac{1}{n}\sum_{i=1}^n(y_i-\overline{y})^2}\] wird als Determinationskoeffizient oder mit den Synonymen Bestimmtheitsmaß und \(R^2\) bezeichnet.
\(d\) gibt an, wie hoch der Anteil in der Varianz der abhängigen Variablen ausfällt, welcher durch die Regression erklärt wird und dient somit als Gütekriterium.
Eine alternative Berechnungsmöglichkeit für \(d\) besteht mit: \[d=r_{BP}^2\] Es kann also gezeigt werden, dass der Determinationskoeffizient dem Quadrat des Korrelationskoeffizienten nach Bravais-Pearson entspricht. Daher resultiert auch das Synonym \(R^2\). Wie aus Abbildung 7.4 hervorgeht, konnten im Beispiel somit rund 74% der Variation in der nachgefragten Menge durch das Regressionsmodell erklärt werden. In der Beurteilung der Güte stützt man sich häufig auf den Richtwerten der Korrelationskoeffizienten. Von einer starken Korrelation haben wir beispielsweise gesprochen, falls \(|r_{BP}|>0,8\). Für \(d=r_{BP}^2\) kann folglich von einem hohen Erklärungsgrad gesprochen werden, falls \(d>0,64\) ist.

Ausreißer

Genau wie beim Korrelationskoeffizienten nach Bravais-Pearson besteht für die Koeffizienten der Regressionsgerade eine Empfindlichkeit gegenüber Ausreißern, was besonders stark in kleinen Datensätzen zum Tragen kommt. Im Code der folgenden Anwendung können Sie das Wertepaar für einen möglichen Ausreißer frei wählen und sehen, wie die Koeffizienten dadurch beeinflusst werden.

7.2 Zeitreihenanalyse

Man unterscheidet Querschnittsdaten und Zeitreihendaten voneinander.
Querschnittsdaten beziehen sich für Bestandsgrößen auf einen festgelegten Zeitpunkt (Beispiel: Alter der Absolventen beim Examen) und für Stromgrößen auf einen festgelegten Zeitraum (Beispiel: Konsumausgaben einzelner Haushalte im Jahr 2019). Betrachtet werden mehrere Merkmalsträger, über die sich für das erhobene Merkmal oder die erhobenen Merkmale der “Querschnitt” ergibt.
Es ist aber auch möglich, für nur einen Merkmalsträger ein bestimmtes Merkmal im Zeitablauf immer wieder neu zu erheben. Man spricht dann von Zeitreihendaten. Dabei müssen die Zeitabstände immer gleich groß gewählt werden. Sofern es sich bei dem Merkmal um eine Stromgröße (Beispiel: Bruttoinlandsprodukt quartalsweise) handeln sollte, so sind die Zeitintervalle für die Stromgröße in gleicher Länge zu wählen (monatlich, quartalsweise, jährlich). Häufig vernachlässigt man dabei allerdings, dass z.B. nicht alle Monate gleich lang sind oder Schaltjahre einen Tag länger dauern. Für Bestandsgrößen (Beispiel: Zahl der Arbeitslosen am Monatsende) gilt, dass die Zeitabstände zwischen den gewählten Zeitpunkten gleich groß zu wählen sind.
Um der zeitlichen Anordnung Rechnung zu tragen, werden die aufeinanderfolgenden Beobachtungen \(x_t\) mit einem Zeitindex \(t\) versehen und fortlaufend mit natürlichen Zahlen durchnummeriert. \[x_1, x_2,\dots,x_n\] Zu jeder Modellzeit \(t\) existiert ein eindeutiger Bezug zur Realzeit. Beginnt beispielsweise die Zeitreihe der Arbeitslosenzahlen im Jahr 2018 mit dem Monat Januar, so erhält dieser die Modellzeit \(t=1\).

7.2.1 additives Komponentenmodell

Dem Komponentenmodell liegt die Idee zugrunde, dass sich Zeitreihendaten aus unterschiedlichen Einflüssen zusammensetzen, welche als Komponenten bezeichnet werden. Sind die beobachteten Zeitreihenwerte das Resultat aus der Summe dieser Komponenten, so spricht man vom additiven Komponentenmodell. Das folgende Komponentenmodell eignet sich häufig zur Modellierung ökonomischer Zeitreihen: \[x_t=\underbrace{T_t+Z_t}_{G_t}+S_t+R_t\]

Dabei gilt:

• \(x_t\) ist der beobachtete Zeitreihenwert zur Modellzeit \(t\).
• \(T_t\) ist die Trendkomponente zur Modellzeit \(t\). Mit der Trendkomponente wird die langfristige Entwicklung der Zeitreihe abgebildet.
• \(Z_t\) ist die zyklische Komponente und dient vor allem für ökonomische Zeitreihen der Modellierung konjunktureller Entwicklungen.
• In Summe bilden \(T_t\) und \(Z_t\) die glatte Komponente \(G_t=T_t+Z_t\), deren Bewegung im Zeitablauf nicht durch starke Fluktuationen geprägt ist, also glatt verläuft.
• \(S_t\) ist die Saisonkomponente und spielt nur bei Zeitreihendaten in unterjähriger Frequenz (z.B. monatlich oder quartalsweise) eine Rolle. Es wird unterstellt, dass die Saison starr ist, d.h. es wird davon ausgegangen, dass sich jedes Jahr dasselbe Saisonmuster wiederholt. Beispielsweise für Quartalsdaten gilt dann \(S_t=S_{t+4} \ \forall \ t\)
  Zudem soll die Summe der Saisonkomponenten über ein Jahr Null entsprechen. Für Quartalsdaten bedeutet dies etwa: \(\sum_{i=1}^4S_{t+i}=0 \ \forall \ t\)
• \(R_t\) ist die Restkomponente, in welcher sich unsystematische Einflüsse sammeln, welche nicht durch die übrigen Komponenten abgebildet werden können. Für das Mittel über alle Restkomponenten wird ein Durchschnittswert von Null angenommen.

Die folgende Grafik veranschaulicht beispielhaft den Verlauf einer Zeitreihe sowie ihre Zerlegung in die einzelnen Komponenten:

7.2.2 Bestimmung der Trendkomponente

Wir beschränken uns auf lineare Trends. Im folgenden wird also davon ausgegangen, dass die langfristige Entwicklung der Zeitreihe linear verläuft. Die Trendkomponente \(T_t\) kann somit in Abhängigkeit der Modellzeit \(t\) formuliert werden als \[T_t=a+b\cdot t\] Es existieren unterschiedliche Ansätze zur Ermittlung der Koeffizienten \(a\) und \(b\).

7.2.2.1 Methode der Reihenhälften

Sofern die Anzahl der vorhandenen Zeitreihenwerte \(n\) gerade ist, wird wie folgt vorgegangen:

Die \(n\) Zeitreihenwerte werden zunächst in zwei gleichgroße Hälften aufgeteilt, so dass jede Hälfte \(n'=\frac{n}{2}\) Zeitreihenwerte enthält. Anschließend werden für die Zeitreihenwerte jeder Hälfte deren arithmetische Mittel berechnet. Die beiden Mittel der Zeitreihenhälften werden dann mit \(\overline{x}_{(1)}\) und \(\overline{x}_{(2)}\) bezeichnet. \(\overline{x}_{(1)}\) und \(\overline{x}_{(2)}\) werden genau den zeitlichen Mitten der beiden Häften zugeordnet. Unter Verwendung der Modellzeit erhält man so zwei Punkte mit folgenden Koordinaten: \[\left(\frac{n'+1}{2},\overline{x}_{(1)} \right), \ \ \left(\frac{3\cdot n'+1}{2},\overline{x}_{(2)} \right)\] Nun wird die Trendgerade \(T_t=a+b\cdot t\) durch die beiden Punkte gelegt.
Die Koeffizienten der Trendgeraden bestimmen sich dann wie folgt: \[b=\frac{\overline{x}_{(2)}-\overline{x}_{(1)}}{n'}\] \[a=\overline{x}_{(1)}-b\cdot \frac{n'+1}{2}\] Die Methode der Reihenhälften wird im folgenden Video erläutert:

Falls die Anzahl der Werte ungerade ist, so wird der mittlere Wert einfach ausgelassen.
Zu beachten ist, dass zwischen den beiden arithmetischen Mitteln der beiden Hälften dann \(n'+1\) Werte liegen und der Steigungskoeffizient der Trendgeraden wie folgt zu berechnen ist: \[b=\frac{\overline{x}_{(2)}-\overline{x}_{(1)}}{n'+1}\] Alle übrigen Berechnungen erfolgen wie für eine gerade Anzahl von Zeitreihenwerten.

Beispiel preisbereinigtes Bruttoinlandsprodukt (BIP)

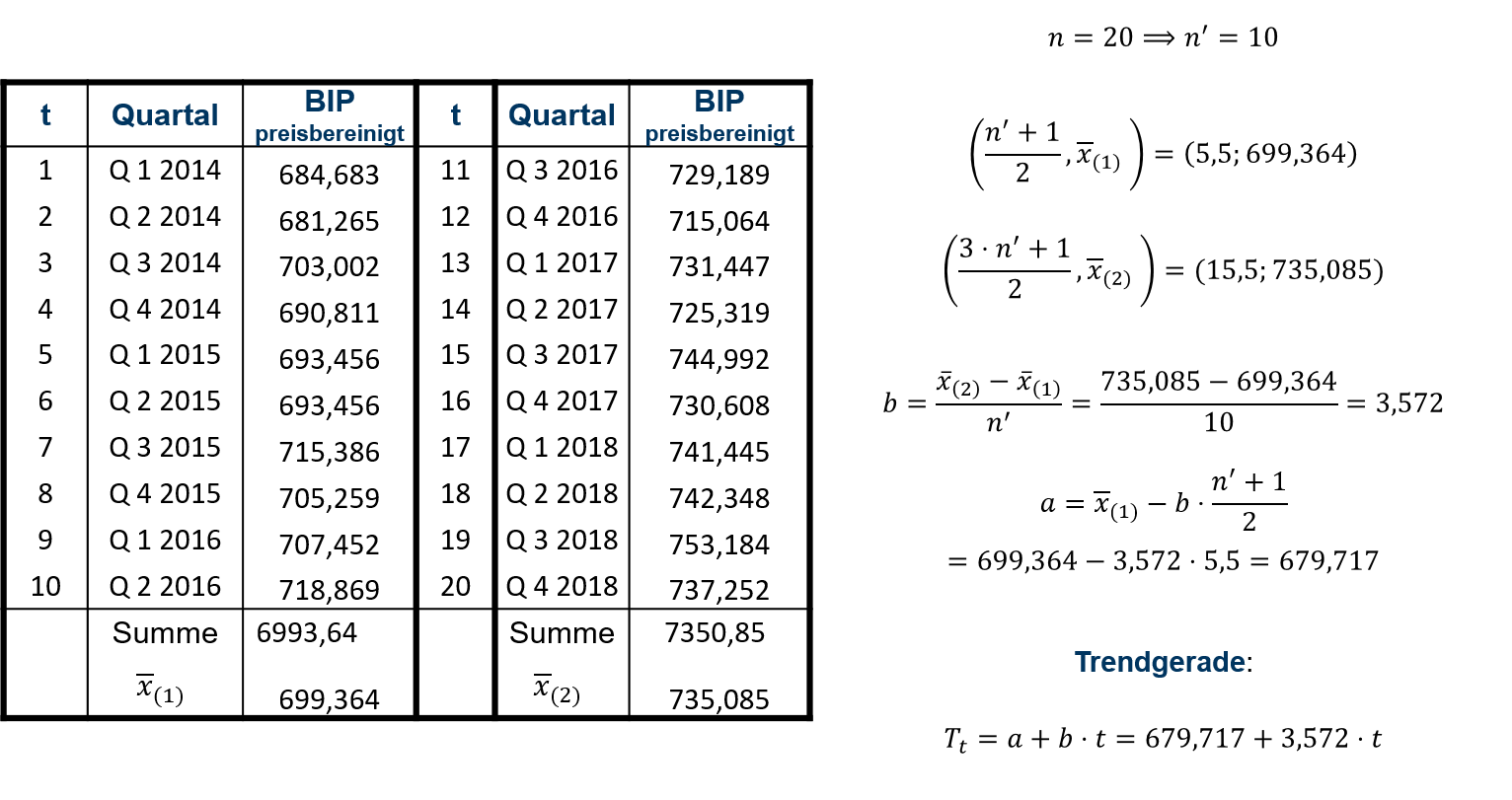
7.5: Methode der Reihenhälften

In Abbildung 7.5 wurde die Trendgerade für das preisbereinigte Bruttoinlandsprodukt in Quartalswerten bestimmt. Die Koeffizienten der Trendgeraden können dann wie folgt interpretiert werden:

• Dem preisbereinigten BIP liegt ein Trendwachstum um 3,572 Mrd. € (Wert von Koeffizient \(b\)) pro Quartal zugrunde.
• Die Trendkomponente entspricht für \(t=0\) dem Koeffizienten \(a\), also \(T_0=a\). \(T_0=679,717\) ist folglich der Wert der Trendkomponente im 4. Quartal des Jahres 2013, welchem eine Modellzeit von \(t=0\) zuzuordnen ist.

Der Verlauf der Zeitreihe und der Trendgeraden ist in Abbildung 7.6 zu sehen.

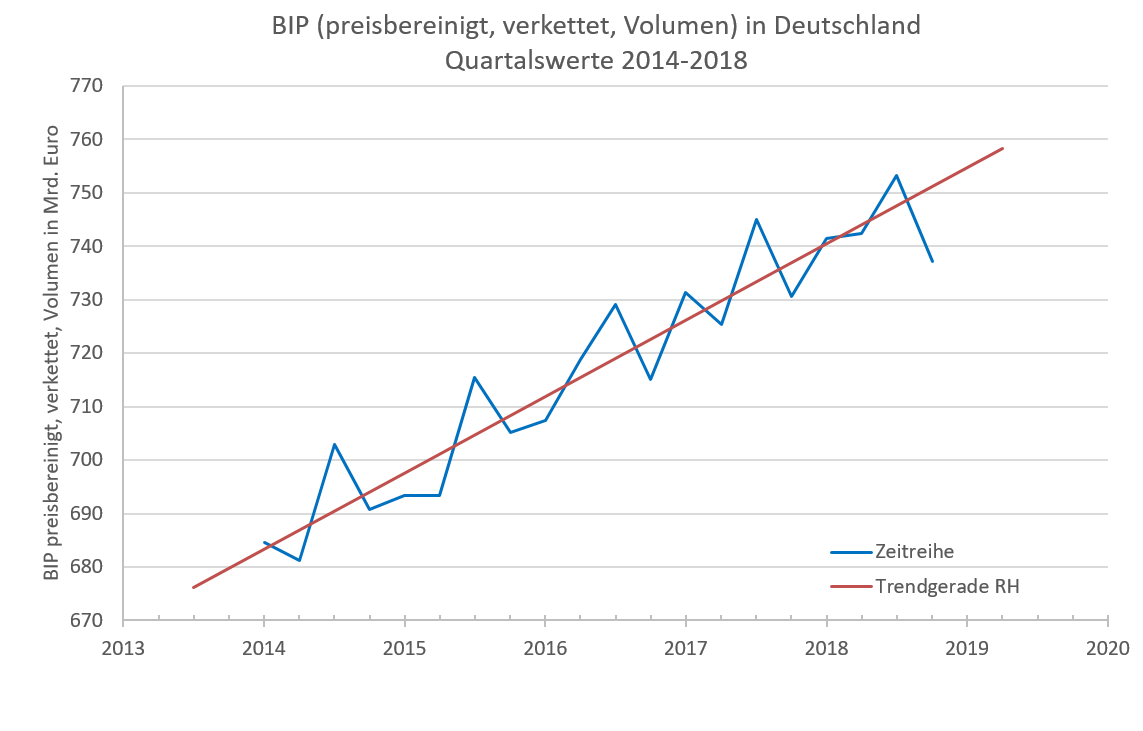
7.6: Zeitreihe BIP, Methode der Reihenhälften

7.2.2.2 Trendbestimmung mit der Methode der Kleinsten Quadrate

Eine weitere, etwas rechenaufwändigere Möglichkeit zur Bestimmung der Trendgeraden bietet die Methode der Kleinsten Quadrate (KQ-Methode). Es wird analog zu Kapitel 7.1 eine Regressionsanalyse durchgeführt, bei der die Zeitreihenwerte \(x_t\) die abhängige Variable darstellen und die Modellzeit \(t\) die unabhängige (erklärende) Variable.
Das Modell lautet: \[x_t=\underbrace{a+b\cdot t}_{T_t}+\underbrace{u_t}_{Z_t+S_t+R_t}\] Die Residuen als \(x_t-T_t=Z_t+S_t+R_t\) setzen sich also aus den übrigen drei Komponenten zusammen.

Bestimmung der Koeffizienten
Prinzipiell erfolgt die Berechnung von \(a\) und \(b\) wie in Kapitel 7.1 beschrieben. Aufgrund der verwendeten Modellzeit kann die Berechnungsvorschrift für den Koeffizienten \(b\) unter Rückgriff auf die Verschiebungssätze für Kovarianzen und Varianzen und Einbezug der Summenformeln für natürliche Zahlen wie folgt vereinfacht werden: \[b=\frac{n\cdot \sum_{t=1}^nx_t\cdot t-\sum_{t=1}^nx_t\cdot\sum_{t=1}^nt}{n \cdot \sum_{t=1}^nt^2-\left(\sum_{t=1}^nt\right)^2}\] wobei \[\sum_{t=1}^nt=\frac{n(n+1)}{2} \ \ \mbox{und} \ \ \sum_{t=1}^nt^2=\frac{n(n+1)(2n+1)}{6}\] Der Koeffizient \(a\) bestimmt sich dann aus: \[a=\frac{\sum_{t=1}^nx_t-b\cdot \sum_{t=1}^nt}{n}=\overline{x}-b\cdot \frac{n+1}{2}\] In Abbildung 7.7 wurde die Trendgerade für das preisbereinigte Bruttoinlandsprodukt in Quartalswerten bestimmt.

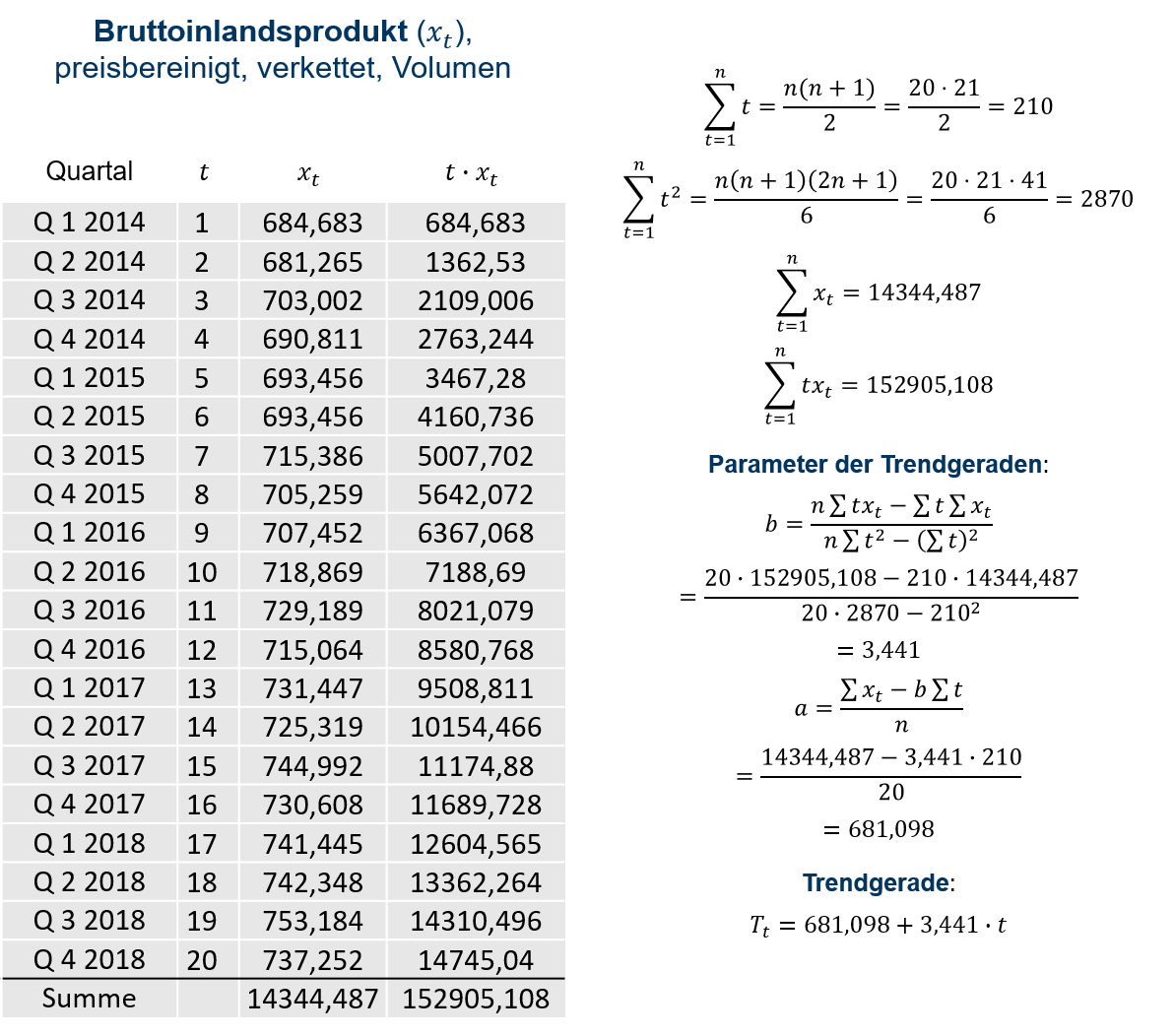
7.7: Trendkomponente, KQ-Methode

Die Interpretation der Koeffizienten erfolgt in analoger Weise zur Methode der Reihenhälften.
Die Bestimmung der Trendgeraden mit der KQ-Methode ist rechenintensiver als die Bestimmung nach der Methode der Reihenhälften. Vorteilhaft ist jedoch, dass mit der KQ-Methode der größtmögliche Teil der Varianz in den Zeitreihenwerten durch die Trendgerade erklärt werden kann.
Abbildung 7.8 zeigt für das BIP von 2014 bis 2018 die Trendgeraden nach beiden Methoden im Vergleich.

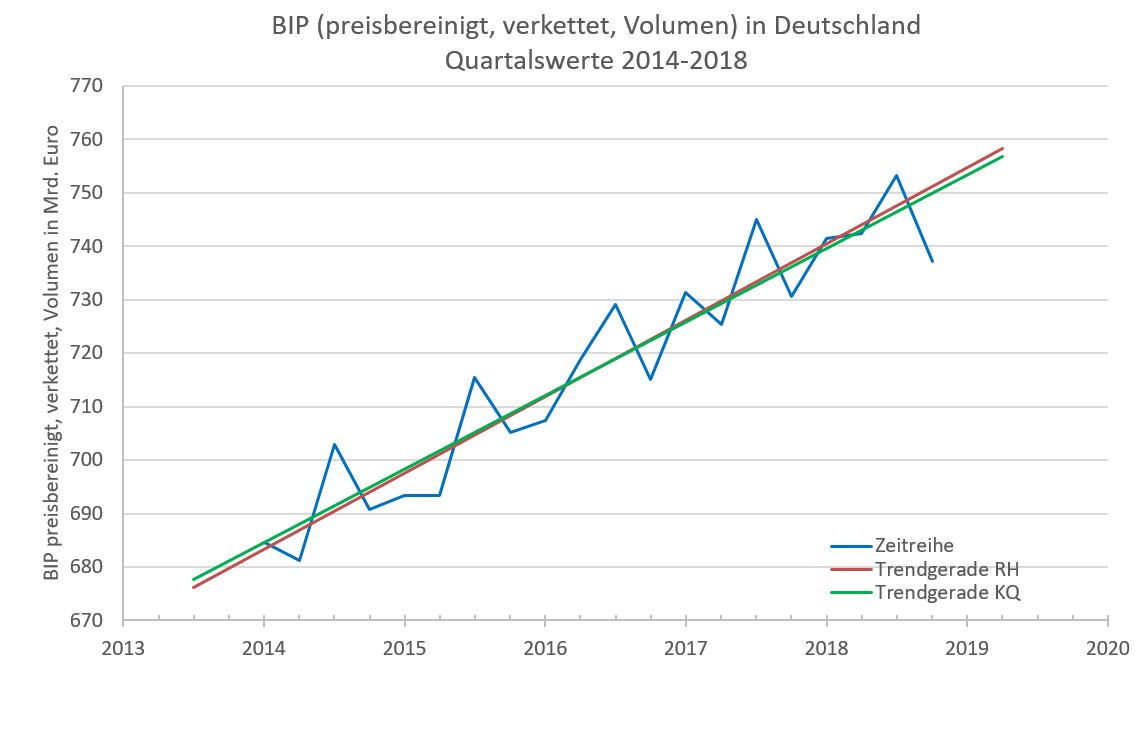
7.8: Trendkomponente, KQ-Methode

7.2.3 Bestimmung der glatten Komponenten

Die glatte Komponente \(G_t=T_t+Z_t\) kann mit der Methode der gleitenden Durchschnitte bestimmt werden. Dabei wird das Ziel verfolgt, die Saisonkomponente \(S_t\) sowie die Restkomponente \(R_t\) durch Mittelung aus der Zeitreihe herauszufiltern und somit zu eliminieren. Saisonbehaftet sind nur Zeitreihen in unterjähriger Frequenz, beispielsweise Quartals- oder Monatswerte. Zeitreihen in jährlicher Frequenz weisen also keine Saisonalität auf.
Da sich die Saisonfigur (das saisonale Muster) per Annahme jedes Jahr in gleicher Weise wiederholt, führt die Mittelung über jene Anzahl aufeinanderfolgender Zeitreihenwerte, welche eine Länge von genau einem Jahr bilden, zu einem Ausschalten der Saisonfigur. Für Quartalsdaten bedeutet dies, dass die Mittelung über 4 aufeinanderfolgende Zeitreihenwerte die Saisonfigur ausschaltet. So könnten beispielsweise die 4 Zeitreihenwerte vom 3. Quartal 2015 bis zum 2. Quartal 2016 gemittelt werden.
Ein Problem besteht nur in der zeitlichen Zuordnung des so gewonnenen Mittelwertes. Grundsätzlich soll das Ziel verfolgt werden, zu einem bestimmten Quartal die glatte Komponente zu bestimmen. Dies gelingt aber nur, wenn im Rahmen der Mittelung aus Perspektive des festgelegten Zeitintervalls genauso viel Vergangenheit wie Zukunft in die Mittelung einfließen.
Abbildung 7.9 zeigt die Berechnung der glatten Komponente für das 3. Quartal 2015. In die Mittelung fließen die gelb unterlegten Zeitreihenwerte ein. Ausgehend vom 3. Quartal 2015 fließt also genauso viel Vergangenheit, wie Zukunft, in die Berechnung ein. Der Mittelwert kann also zeitlich dem 3. Quartal 2015 zugeordnet werden. Die Mittelung erstreckt sich allerdings über 5 Quartale, obwohl bereits 4 aufeinanderfolgende Quartale das vollständige Saisonmuster abbilden. Problematisch scheint, dass das erste und letzte Quartal in der Mittelung, jeweils vom gleichen Saisontyp (jeweils Q1) ist. Damit die Saisonalität aller Quartale insgesamt ein gleiches Gewicht erhält, werden der erste und letzte Wert in der Mittelung mit dem Faktor \(\frac{1}{2}\) gewichtet. Schließlich sind somit die saisonalen Besonderheiten aller Quartale in gleicher Stärke vertreten und die Mittelung führt dazu, dass die Saisonfigur eliminiert wird.
Zudem schwindet auch die Restkomponente \(R_t\) mit zunehmender Mittelung von Zeitreihenwerten, weshalb der mit \(\overline{x}_7=703,641\) gewonnene Mittelwert als glatte Komponente \(G_7\) bezeichnet werden kann.

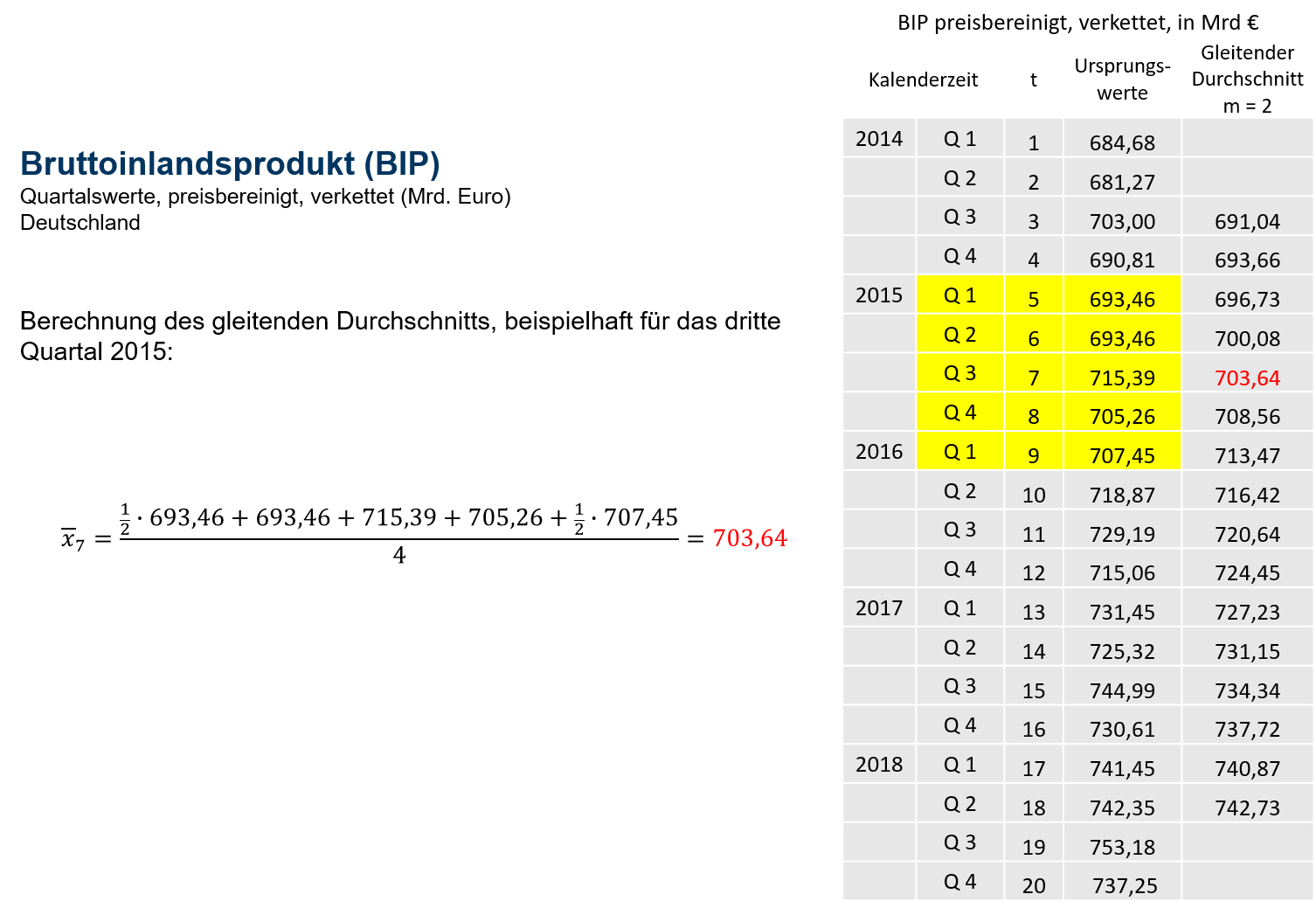
7.9: glatte Komponente, Methode der gleitenden Durchschnitte

gleitende Durchschnitte über Quartalswerte

Wie in Abbildung 7.9 zu sehen, ist also für Zeitreihen in vierteljährlicher Frequenz die folgende Berechnungsformel zu verwenden:

\[\overline{x}_t=\frac{\frac{1}{2}\cdot x_{t-2}+x_{t-1}+x_t+x_{t+1}+\frac{1}{2}\cdot x_{t+2}}{4}\]

Das gelb unterlegte Fenster zeigt den sogenannten Stützbereich an, also welche Werte in die Berechnung einfließen. Das Fenster ist um einen Wert weiter nach unten zu verschieben, falls für die Modellzeit \(t=8\) die glatte Komponente \(G_8=\overline{x}_8\) zu berechnen ist usw.
Man erkennt schnell, dass für den aktuellen Rand, mit den Quartalen 3 & 4 des Jahres 2018, keine glatten Komponenten bestimmt werden können, weil dafür die Werte der Quartale 1 & 2 aus dem Jahr 2019 benötigt würden. Gleiches Problem stellt sich für die Quartale 1 & 2 aus dem Jahr 2014 ein.

Abbildung 7.10 zeigt die Zeitreihe der Ursprungswerte \(x_t\) sowie den Verlauf der glatten Komponente \(G_t\). Die zyklische Komponente \(Z_t\) kann aus der glatten Komponente \(G_t\) mit der Differenz \(Z_t=G_t-T_t\) isoliert werden. Die Trendkomponente kann dabei mit der Methode der Reihenhälften oder der Methode der Kleinsten Quadrate bestimmt werden.

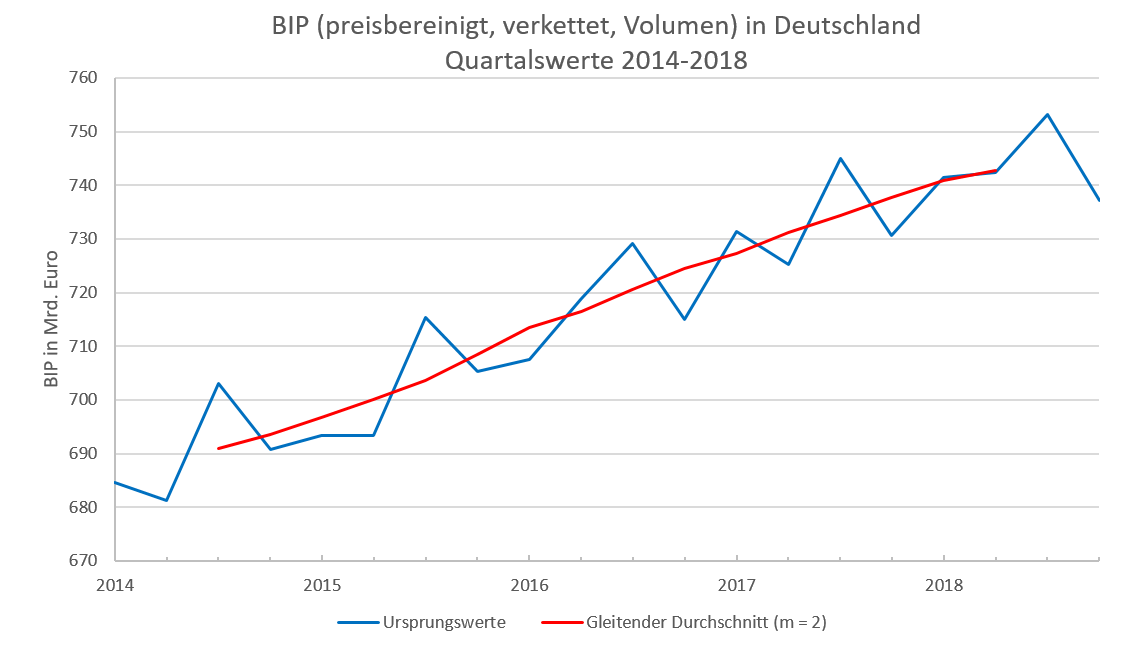
7.10: Ursprungswerte und glatte Komponente

gleitende Durchschnitte über Monatswerte

Liegt die Zeitreihe in monatlicher Frequenz vor, so ist die folgende Berechnungsformel für die glatte Komponente zu verwenden:

\[\overline{x}_t=\frac{\frac{1}{2}\cdot x_{t-6}+x_{t-5}+ \dots x_t+\dots x_{t+5}+\frac{1}{2}\cdot x_{t+6}}{12}\]

allgemeine Berechnungsvorschrift für eine gerade Anzahl unterjähriger Zeitreihenwerte

Allgemeiner lässt sich schreiben: \[\overline{x}_t=\frac{\frac{1}{2}\cdot x_{t-m}+ \dots + x_t+\dots +\frac{1}{2}\cdot x_{t+m}}{2m}\]

\(m\) legt das Berechnungsfenster (Stützbereich) fest und gibt somit die Anzahl der Zeitreihenwerte an, welche vor bzw. nach \(x_t\) in die Berechnung einfließen.

• \(m=1\) für Halbjahresdaten
• \(m=2\) für Quartalsdaten
• \(m=6\) für Monatsdaten

Isolation der zyklischen Komponente

Durch Kombination der Methode der Reihenglättung und einer der Methoden der Trendbestimmung, kann die zyklische Komponente isoliert werden, denn \[G_t=T_t+Z_t \Leftrightarrow Z_t=G_t-T_t\] Die zyklische Komponente des dritten Quartals zum Jahr 2015, also \(Z_7\), kann für das vierteljährliche BIP durch Kombination der Methode der Reihenglättung und der Trendbestimmung mit der Methode der Kleinsten Quadrate wie folgt berechnet werden:

\[T_7=681,098+3,441\cdot 7=705,185\] Unter Rückgriff auf die schon berechnete glatte Komponente \(G_7=703,641\) gilt dann:

\[Z_7=703,641-705,185=-1,544 \]