Kapitel 9 Indexzahlen

Bekannte Indexzahlen sind beispielsweise der Deutsche Aktienindex (DAX) oder der Verbraucherpreisindex (VPI).
Indexzahlen verfolgen das Ziel der Informationsverdichtung zu einer vorher abgegrenzten Gruppe gleichartiger Tatbestände. Für den DAX erfolgt die Abgrenzung der für die Berechnung zu berücksichtigen 40 “größten” Unternehmen nach dem Kriterium Börsenwert.
Im VPI werden jene Waren und Dienstleistungen erfasst, welche von den Verbrauchern besonders stark nachgefragt werden und daher das Verbraucherverhalten eines Durchschnittshaushaltes gut abbilden.
Für die festgelegte Gruppe wird dann die Veränderung eines bestimmten Merkmals über die Zeit in Form einer Veränderungszahl, der Indexzahl, zusammengefasst.
Für die 40 DAX Unternehmen ist dieses Merkmal der Börsenwert der Unternehmen, wobei für den DAX-Performanceindex Dividendenzahlung miteinzubeziehen sind. Der VPI stellt auf das Merkmal “Preis” der jeweiligen Waren und Dienstleistungen ab.

9.1 Grundbausteine für Preisindizes

Der VPI wird als gewichtetes Mittel von Preismesszahlen (vgl. Kapitel 8.2.3) berechnet, welche sich alle auf dasselbe Basisjahr \(0\) und dasselbe Berichtsjahr \(t\) beziehen.
In der Konstruktion der Indexformeln werden die \(n\) als Güter bezeichneten Waren und Dienstleistungen durch Zuweisung einer natürlichen Zahl von \(i \in \{1,...,n\}\) voneinander abgegrenzt.

• \(p_i(t)\) bezeichnet dann den Preis von Gut \(i\) aus der Berichtsperiode \(t\) und \(p_i(0)\) ist der Preis aus der Basisperiode \(0\).
  
• Die Preismesszahl gibt dann bezogen auf Berichts- und Basisperiode den Preisänderungsfaktor von Gut \(i\) an und lautet: \[\frac{p_i(t)}{p_i(0)}\]
• Mit \(q_i(t)\) bzw. \(q_i(0)\) werden die Mengeneinheiten für Gut \(i\) aus der Berichts- bzw. Basisperiode bezeichnet. Bezieht sich der Preis für ein bestimmtes Gut beispielsweise auf eine Menge von 500g, so wird durch die Mengen \(q_i(t)\) und \(q_i(0)\) angegeben, wie viele 500g Einheiten in der Berichts- bzw. Basisperiode konsumiert worden sind.

9.2 Preisindex nach Laspeyres

Mit dem Preisindex nach Laspeyres wird das Ziel verfolgt, für die \(n\) Güter des Warenkorbs die durchschnittliche Preisänderung zu messen, welche von Änderungen in den Mengen zwischen Basis- und Berichtsperiode unbeeinflusst ist. Es existieren drei Darstellungsformen für den Preisindex nach Laspeyres, welche ineinander überführt werden können.

Aggregatform

Die Aggregatform ist die bekannteste Darstellung und lautet:

\[PL(0,t)=\frac{\sum_{i=1}^n p_i(t)\cdot q_i(0)}{\sum_{i=1}^n p_i(0) \cdot q_i(0)}\]

Änderungen in den Mengen kommen nicht zum Tragen, da im Zähler wie im Nenner mit \(q_i(0)\) das Verbraucherverhalten aus der Basisperiode zugrunde gelegt wird. Im Nenner finden sich somit die Gesamtausgaben für die \(n\) Güter aus der Basisperiode. Im Zähler hingegen stehen fiktive Ausgaben auf Basis der Preise der Berichtsperiode, welche an den Mengen aus der Basisperiode festhalten.

allgemeine Gewichte

Die Aggregatform kann durch Ergänzung einfach in die Berechnungsform mit den allgemeinen Gewichten \(w_i(0)=p_i(0)\cdot q_i(0)\) überführt werden und lautet:

\[PL(0,t)=\frac{\sum_{i=1}^n\frac{p_i(t)}{p_i(0)}\cdot w_i(0)}{\sum_{i=1}^n w_i(0)}\]

normierte Gewichte

Zieht man für die Darstellung mit allgemeinen Gewichten den Kehrwert der Gesamtausgaben, also \(\frac{1}{\sum_{i=1}^n w_i(0)}\), mit in die Zählersumme, so stellen die normierten Gewichte \(g_i(0)=\frac{w_i(0)}{\sum_{i=1}^n w_i(0)}\) die Ausgabenanteile der Güter aus dem Basisjahr dar. Die Berechnungsformel lautet dann:

\[\sum_{i=1}^n \frac{p_i(t)}{p_i(0)}\cdot g_i(0)\]

Abbildung 9.1 zeigt die Überführung in die drei Darstellungsformen.

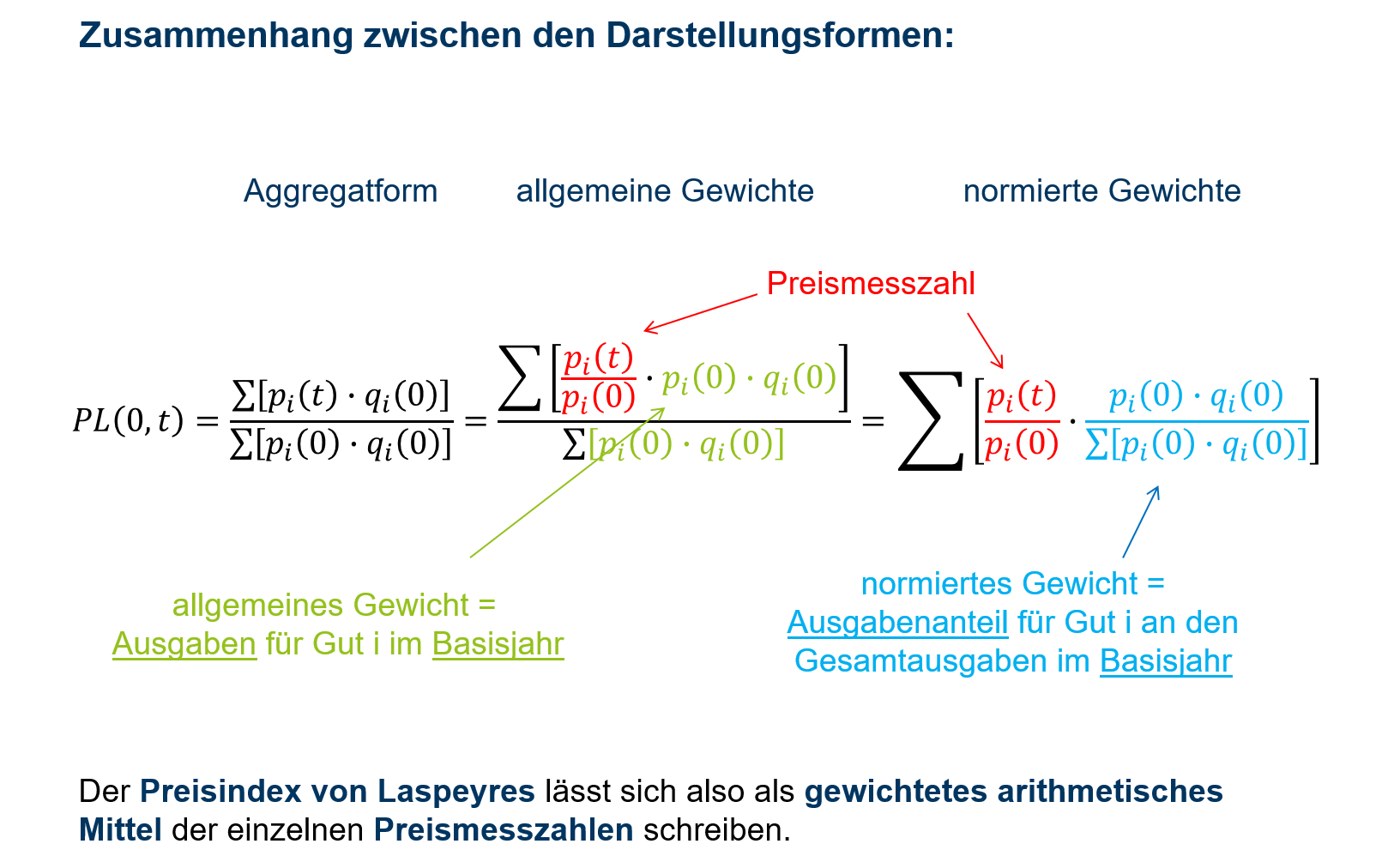
9.1: Darstellungsformen Preisindex nach Laspeyres

Abbildung 9.2 zeigt für ein einfaches Zahlenbeispiel, wie und auf Basis welcher Informationen die drei Formeln anzuwenden sind.

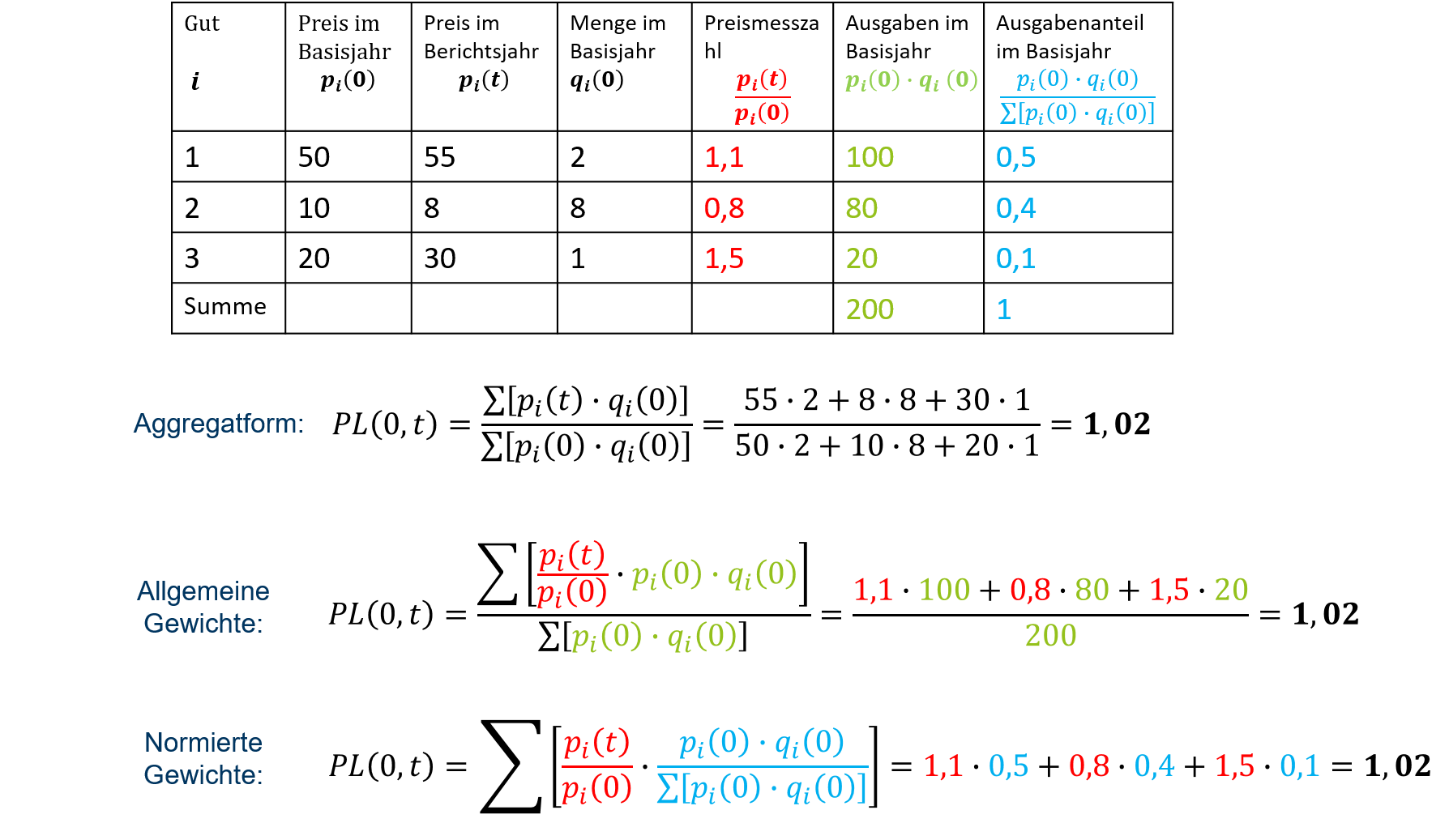
9.2: Anwendung der verschiedenen Darstellungsformen, Laspeyres

In der praktischen Durchführung kommt für die Ermittlung des VPI die Darstellung mit normierten Gewichten zum Einsatz. Die Gewichtung (Wägung) der Preismesszahlen erfolgt mit den Ausgabeanteilen. Die Gesamtheit der Ausgabeanteile wird daher auch als Wägungsschema bezeichnet. Das Wägungsschema bezieht sich auf das Basisjahr und bleibt somit unverändert, solange das Basisjahr beibehalten wird. Einzig die Preismesszahlen müssen für jede Periode neu ermittelt werden.
Der Preisindex nach Laspeyres kann also als gewichtetes arithmetisches Mittel der Preismesszahl berechnet werden und somit auch als Preismesszahl für das gesamte Güterbündel interpretiert werden. Der Preisindex kann somit als Preisänderungsfaktor für das betrachtete Güterbündel von der Basis- zur Berichtsperiode angesehen werden. Üblicherweise wird der Preisindex in Prozent angegeben, also mit 100 multipliziert, ohne aber das Prozentzeichen dabei anzugeben. Die folgenden Kenngrößen können für eine weitere Interpretation bestimmt werden:

9.2.1 wichtige Kennzahlen zum Preisindex

• Preisveränderungsrate vom Basis- zum Berichtsjahr

\[\frac{PL(0,t)-PL(0,0)}{PL(0,0)}=\frac{PL(0,t)}{100}-1 \quad \mbox{wegen} \ \ PL(0,0)=100\]

• Inflationsrate

\[\frac{PL(0,t)}{PL(0,t-1)}-1\] Mit der Inflationsrate wird also die Änderungsrate des Preisindex im Vergleich zum Vorjahr bezeichnet.

• jahresdurchschnittliche Inflationsrate im Zeitraum \(t_1\) bis \(t_2\), \(t_2>t_1\)

\[\left(\frac{PL(0,t_2)}{PL(0,t_1)}\right)^\frac{1}{t_2-t_1}-1\] Die jahresdurchschnittliche Inflationsrate entspricht also jener konstanten Inflationsrate, welche für den Zeitraum von \(t_1\) bis \(t_2\) hätte gelten müssen, um eine Veränderung des Preisindex von \(PL(0,t_1)\) auf \(PL(0,t_2)\) zu erreichen.

• Kaufkraft

\[KK(0,t)=\frac{PL(0,0)}{PL(0,t)}\] Die Kaufkraft gibt den relativen Wert des Geldes im Berichtsjahr \(t\) verglichen mit dem Basisjahr \(0\) an. So würde eine Verdopplung der Preise mit einer Kaufkraft von 50% einhergehen, da man mit dem gleichen Geldbetrag wie im Jahr \(0\) im Jahr \(t\) nur noch die Hälfte der Güter bekommen würde.

• Kaufkraftänderungsrate im Vergleich zum Basisjahr

\[\frac{PL(0,0)}{PL(0,t)}-1\]

Hintergrund: \[\frac{KK(0,t)}{KK(0,0)}-1=\frac{\frac{PL(0,0)}{PL(0,t)}}{\frac{PL(0,0)}{PL(0,0)}}-1=\frac{PL(0,0)}{PL(0,t)}-1\]

• Kaufkraftänderungsrate im Vorjahresvergleich

\[\frac{PL(0,t-1)}{PL(0,t)}-1\]

Hintergrund: \[\frac{KK(0,t)}{KK(0,t-1)}-1=\frac{\frac{PL(0,0)}{PL(0,t)}}{\frac{PL(0,0)}{PL(0,t-1)}}-1=\frac{PL(0,t-1)}{PL(0,t)}-1\]

• jahresdurchschnittliche Kaufkraftänderungsrate im Zeitraum \(t_1\) bis \(t_2\), \(t_2>t_1\)

\[\left(\frac{PL(0,t_1)}{PL(0,t_2)}\right)^\frac{1}{t_2-t_1}-1\]

Hintergrund zum Änderungsfaktor der Kaufkraft in der Klammer: \[\frac{KK(0,t_2)}{KK(0,t_1)}=\frac{\frac{PL(0,0)}{PL(0,t_2)}}{\frac{PL(0,0)}{PL(0,t_1)}}=\frac{PL(0,t_1)}{PL(0,t_2)}\]

Im folgenden Video werden die genannten Kennzahlen auf Basis des VPI ermittelt.

9.2.2 Vor- und Nachteile der Indexformel nach Laspeyres

Vorteile

Solange an einem Basisjahr festgehalten wird, müssen nur die Preise \(p_i(t)\) fortlaufend neu erhoben werden. Eine aufwendige jährliche Neubestimmung des Wägungsschemas (der Ausgabeanteile) entfällt somit.
Zudem sind zwei Preisindizes aus unterschiedlichen Berichtsjahren gut vergleichbar miteinander, da deren Wägungsschema mit gleichem Basisjahr identisch ist. Für die Ermittlung von Inflationsraten hat dies zur Folge, dass wünschenswerterweise somit einzig Preiseffekte Einfluss auf die Inflationsraten haben.
Der Preisindex von Laspeyres ist aggregierbar. D.h., dass das gesamte Güterbündel thematisch aufgegliedert werden kann und für die resultierenden Teile jeweils Preisindizes berechnet werden können, die dann als gewichtetes arithmetische Mittel wieder den Gesamtindex ergeben. Im Gegensatz zur Indexformel nach Laspeyres weisen viele andere Indexformeln diese Eigenschaft der Aggregierbarkeit nicht auf.

Nachteile

Mit zunehmendem Zeitabstand zwischen Berichts- und Basisjahr veraltert das Wägungsschema und spiegelt daher nicht mehr die aktuellen Verbrauchsgewohnheiten wider. Dies führt häufig zum sogenannten Laspeyres-Effekt. Dieser bezeichnet einen zu hoch ausgewiesenen Preisindex infolge der Nicht-Berücksichtigung von Gütersubstitutionen.
Steigen beispielsweise die Preise für Rindfleisch sehr stark an, während sich Geflügel kaum verteuert, so werden die Verbraucher tendenziell Rindfleisch durch Geflügel substituieren. Hält man jedoch am Wägungsschema aus der Vergangenheit (dem Basisjahr) fest, so werden die starken Preisanstiege beim Rindfleisch übermäßig stark gewichtet, was zu einem starken Anstieg des Preisindex führt.

In der Abwägung der Vor- und Nachteile hat man sich in Deutschland in der Berechnungspraxis des VPI darauf verständigt, das Wägungsschema im Rhythmus von 5 Jahren zu aktualisieren. Dadurch erhält man mit jeder Revision, in der man das Wägungsschema neu ermittelt und den Index von diesem Jahr an neu berechnet, immer wieder neue Indexzeitreihen mit neuen Basisjahren und Wägungsschemata, wie dies z. B. in Abbildung 9.3 zu erkennen ist.

9.3: Indexreihen Verbraucherpreisindex

9.2.3 Umbasierung

Als Umbasierung wird die rechnerische Umstellung eines Index auf ein neues Basisjahr bezeichnet. Ziel ist es, Indizes, welche auf unterschiedliche Basisjahre berechnet wurden, miteinander vergleichbarer zu machen. Die Umbasierung für den Index erfolgt dabei analog zur Umbasierung einzelner Messzahlen, die in Kapitel 8.2.3 dargestellt wurden. Für den Preisindex nach Laspeyres ergibt sich durch die Umbasierung vom Basisjahr \(0\) auf das Basisjahr \(s\): \[PL(s,t)_{umbasiert}=\frac{PL(0,t)}{PL(0,s)}=\frac{\sum_{i=1}^n p_i(t)\cdot q_i(0)}{\sum_{i=1}^n p_i(s)\cdot q_i(0)}\] Der umbasierte Index entspricht also nur dann tatsächlich dem Index \(PL(s,t)=\frac{\sum_{i=1}^n p_i(t)\cdot q_i(s)}{\sum_{i=1}^n p_i(s)\cdot q_i(s)}\), falls das Mengengerüst der Perioden \(0\) und \(s\) identisch ist, also \(q_i(0)=q_i(s) \ \forall \ i\).

9.2.4 Verkettung

Als Verkettung wird die multiplikative Verknüpfung von zwei Indexzahlen über eine Periode \(s\) bezeichnet, welche die Basisperiode der einen und die Berichtsperiode der anderen Indexzahl darstellt. So können aus Indexzeitreihen mit unterschiedlichen Basisjahren lange Zeitreihen erzeugt werden.

\[PL(0,t)_{verkettet}=PL(0,s)\cdot PL(s,t)=\frac{\sum_{i=1}^np_i(s)\cdot q_i(0)}{\sum_{i=1}^n p_i(0)\cdot q_i(0)}\cdot \frac{\sum_{i=1}^n p_i(t)\cdot q_i(s)}{\sum_{i=1}^n p_i(s)\cdot q_i(s)}\] Auch hier gilt, dass der verkettete Index \(PL(0,t)_{verkettet}\) nur dann \(PL(0,t)=\frac{\sum_{i=1}^np_i(t)\cdot q_i(0)}{\sum_{i=1}^n p_i(0)\cdot q_i(0)}\) entspricht, falls \(q_i(0)=q_i(s) \ \forall \ i\).

Die Aufgabenstellungen zur Umbasierung und Verkettung aus Abbildung 9.3 werden im folgenden Video bearbeitet:

9.3 Verbraucherpreisindex (VPI)

Der VPI wird in Deutschland mit der Laspeyresformel bestimmt. Zuständig ist das Statistische Bundesamt mit Unterstützung durch die jeweiligen Landesämter. Da der VPI für jeden Monat eines jeden Jahres bestimmt wird, müssen auch monatlich Preiserhebungen durchgeführt werden. Aus den Preisen werden dann die Preismesszahlen ermittelt. Die Gewichtung der Preismesszahlen erfolgt für die Indexberechnung mit den Ausgabeanteilen der jeweiligen Güter. Die Ausgabeanteile bilden das Wägungsschema und werden in der Regel alle 5 Jahre im Rahmen der Einkommens- und Verbrauchsstichprobe neu bestimmt. Das zugrundeliegende Jahr des Wägungsschemas entspricht dann dem Basisjahr. Das Wägungschema untergliedert sich in 12 Hauptgruppen. Innerhalb der Hauptgruppen erfolgt eine weitere Untergliederung.
Aufgrund der Aggregationseigenschaft der Laspeyresfomel können für die einzelnen Hauptgruppen jeweils Preisindizes bestimmt werden, aus denen dann der Gesamtindex über alle Gruppen ermittelt werden kann. Abbildung 9.4 zeigt für die 12 Hauptgruppen die in Promille angegebenen Ausgabeanteile an den Gesamtausgaben.

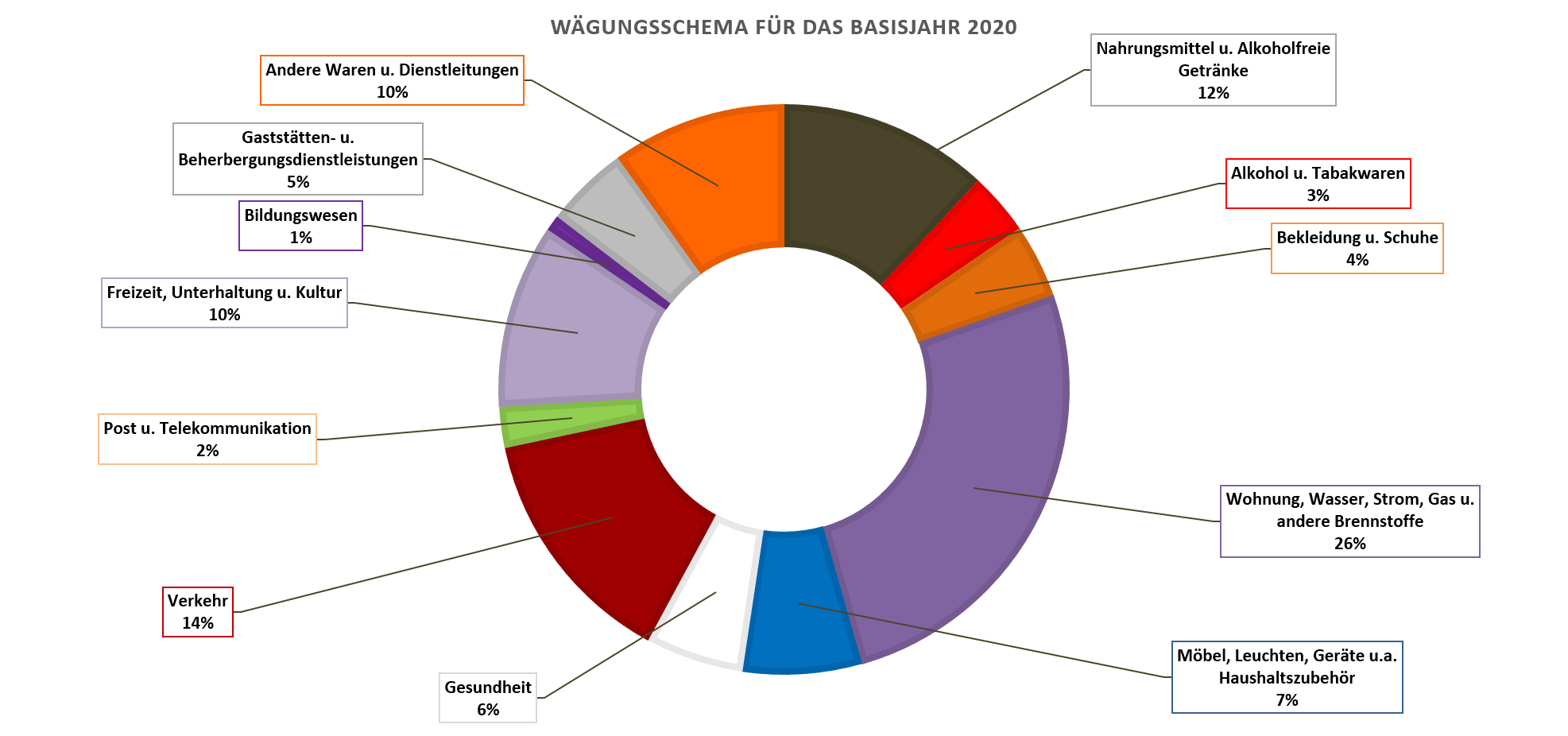
9.4: VPI nach Hauptgruppen

Der Gesamtindex wird dann als gewichtetes arithmetisches Mittel aus den Preisindizes der einzelnen Gruppen berechnet, welche auch als Teilindizes bezeichnet werden. Als Gewichte dienen die Ausgabeanteile aus dem Basisjahr. Die Berechnung des Gesamtindex aus den Teilindizes für das Berichtsjahr 2022 mit Basisjahr 2020 kann in Abbildung 9.5 nachvollzogen werden.

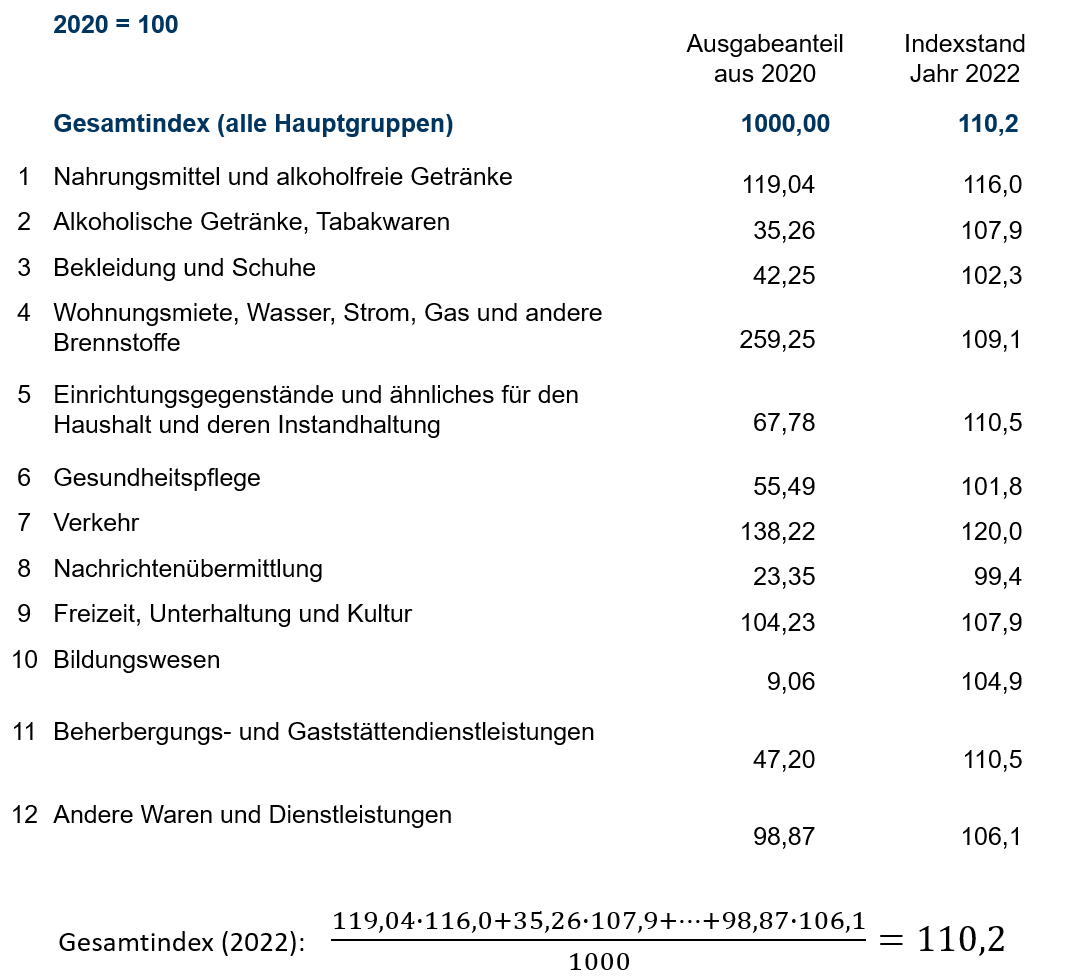
9.5: Berechnung des Gesamtindex auf Basis der Teilindizes

>

9.4 Preisindex nach Paasche

Ein wesentlicher Kritikpunkt am Preisindex von Laspeyres richtet sich gegen das lange “Festhalten” an Gewichten aus dem Basisjahr, welche mit zunehmendem Abstand zum Basisjahr weniger repräsentativ für die aktuellen Verbrauchsgewohnheiten sind. Beim Preisindex von Paasche stammen diese Gewichte aus dem Berichtsjahr und werden somit für jedes Berichtsjahr erneut aktualisiert.

Es existieren drei Darstellungsformen für den Preisindex nach Paasche, welche ineinander überführt werden können.

Aggregatform

Die Aggregatform ist die bekannteste Darstellung und lautet:

\[PP(0,t)=\frac{\sum_{i=1}^n p_i(t)\cdot q_i(t)}{\sum_{i=1}^n p_i(0) \cdot q_i(t)}\]

Änderungen in den Mengen kommen nicht zum Tragen, da im Zähler wie im Nenner mit \(q_i(t)\) das Verbraucherverhalten aus der Berichtsperiode zugrunde gelegt wird. Im Zähler finden sich somit die Gesamtausgaben für die \(n\) Güter aus der Berichtsperiode. Im Nenner hingegen stehen fiktive Ausgaben auf Basis der Preise der Basisperiode, welche sich an den Mengen der Berichtsperiode orientieren.

allgemeine Gewichte

Die Aggregatform kann durch Ergänzung einfach in die Berechnungsform mit den allgemeinen Gewichten \(w_i(t)=p_i(t)\cdot q_i(t)\) überführt werden und lautet:

\[PP(0,t)=\frac{\sum_{i=1}^n w_i(t)}{\sum_{i=1}^n \frac{p_i(0)}{p_i(t)} \cdot w_i(t)}\]

Die allgemeinen Gewichte entsprechen also den Ausgaben der Güter im Berichtsjahr.

normierte Gewichte

Zieht man für die Darstellung mit allgemeinen Gewichten den Kehrwert der Zählersumme, also \(\frac{1}{\sum_{i=1}^n w_i(t)}\), mit in die Nennersumme, so stellen die normierten Gewichte \(g_i(t)=\frac{w_i(t)}{\sum_{i=1}^n w_i(t)}\) die Ausgabenanteile der Güter aus dem Berichtsjahr dar. Die Berechnungsformel lautet dann:

\[ \frac{1}{\sum_{i=1}^n\frac{p_i(0)}{p_i(t)}\cdot g_i(t) }\]

Der Preisindex nach Paasche kann somit als gewichtetes harmonisches Mittel der Preismesszahlen bestimmt werden, wobei wahlweise die Ausgaben \(w_i(t)\) oder die Ausgabeanteile \(g_i(t)\) als Gewichte dienen.

Abbildung 9.6 zeigt die Überführung in die drei Darstellungsformen.

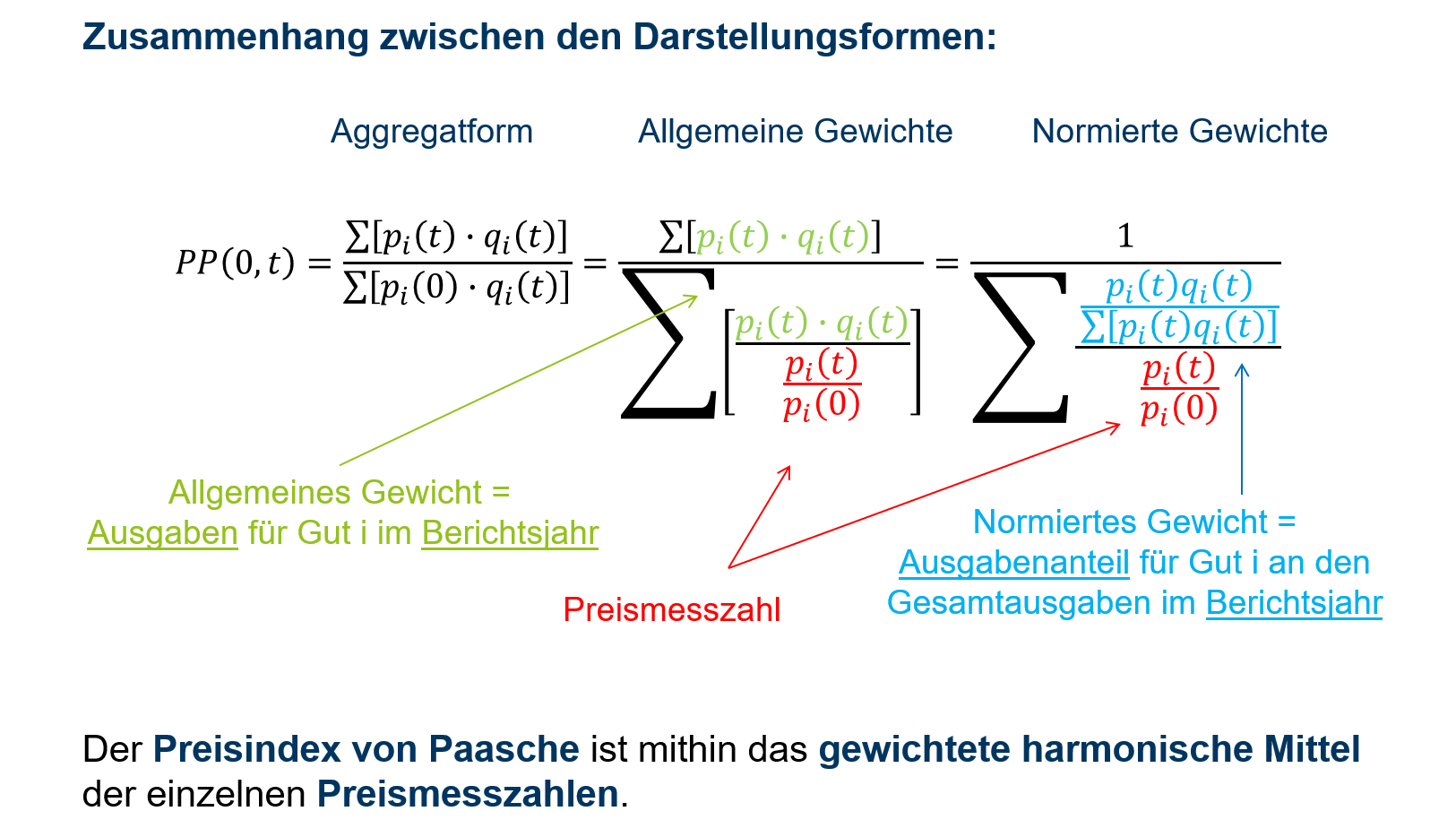
9.6: Darstellungsformen Preisindex nach Paasche

Abbildung 9.7 zeigt für ein einfaches Zahlenbeispiel, wie und auf Basis welcher Informationen die drei Formeln anzuwenden sind.

9.7: Anwendung der verschiedenen Darstellungsformen, Paasche

Dem Vorteil einer hohen Repräsentativität durch Berücksichtigung der immer aktuellen Gewichte aus dem Berichtsjahr \(t\) steht das Problem der Vergleichbarkeit der Indexzahlen aus unterschiedlichen Berichtsjahren gegenüber. Würde man auf Basis des Paascheindex die Inflationsrate ermitteln, so kämen im Vergleich der Perioden \(t\) und \(t-1\) unterschiedliche Gebrauchsgewohnheiten zum Einsatz. Die Inflationsrate wäre dann nicht mehr allein auf Veränderungen in den Preisen zurückzuführen.
Das Hauptanwendungsgebiet des Preisindex nach Paasche ist die Bereinigung von Volumengrößen um Preiseffekte (Deflationierung). So kann beispielsweise das reale (preisbereinigte) Bruttoinlandsprodukt (BIP) aus dem nominellen BIP (in jeweiligen Preisen) wie folgt bestimmt werden:

\[BIP_{real(0)}=\frac{BIP_{nominal(t)}}{PP(t,0)} \]

Dabei ist \(BIP_{nominal(t)}=\sum_{i=1}^n p_i(t)\cdot q_i(t)\) das BIP in Preisen der Berichtsperiode \(t\) und \(BIP_{real(0)}=p_i(0)\cdot q(t)\) das BIP in Preisen der Basisperiode \(0\).

Seit dem Jahr 2005 wird das reale BIP als Kettenindex auf Vorjahrespreisbasis ermittelt, was mit einem Preisindex nach Paasche als impliziten Deflator einhergeht. Dies soll hier aber nicht weiter vertieft werden.

9.4.1 Beispielaufgabe Indexberechnung

Der Preisindex nach Laspeyres und der Preisindex nach Paasche sollen für das Berichtsjahr 2016 zum Basisjahr 2015 auf Basis der Informationen aus Abbildung 9.8 ermittelt werden.

9.8: Beispielaufgabe Indexberechnung

Die Lösung der Aufgabenstellung finden Sie im folgenden Video: