Kapitel 3 Quantile und Mittelwerte
3.1 Quantile
Um eine persönliche Leistung einordnen zu können, geht man meistens auf die Suche nach einem Quantil, selbst ohne den Begriff Quantil jemals gehört zu haben. So stellt sich oft die Frage, gehöre ich mit meiner Leistung zu den besseren 50% oder vielleicht sogar zu den besten 10%? Dafür ist zunächst zu klären, welcher Wert in die entsprechenden zwei Hälften über und unter diesem Wert trennt, so dass ich meine Leistung einordnen kann.
Quantile können folglich erst ab Ordinalskalenniveau bestimmt werden.
Mit der Vorgabe eines bestimmten Prozentsatzes, welcher in Form von \(p\) als Dezimalwert angegeben wird, mit \(0<p<1\), wird festgelegt, wie groß der Anteil an der Gesamtzahl der Beobachtungen höchstens ist, welcher unter den gesuchten Wert \(\tilde{x}_p\) fällt. Zugleich dürfen im Anteil höchstens \(1-p\) der Beobachtungen über \(\tilde{x}_p\) liegen.
Ob ich mit der erreichten Punktzahl in meiner Klausur nun zu den besten 10% gehöre, erkenne ich daran, ob meine Punktzahl oberhalb von \(\tilde{x}_{0,9}\) liegt. Im folgenden Beispiel finden sich die Punktzahlen von 10 Studierenden für eine Statistik-Klausur, in der höchstens 20 Punkte erzielt werden konnten.
3.1: Datenlage A, Punktzahl in Klausur
Gesucht wird also jener Wert, für den gilt, dass höchstens 90% der Beobachtungen darunter liegen und 10% der Beobachtungen darüber liegen.
Betrachten wir den Beobachtungswert 17, so ist festzuhalten, dass 80% der Beobachtungen unter diesem Wert liegen und 10% über diesem Wert liegen. Zwar erfüllt der Beobachtungswert 17 die Definition des 0,9-Quantils, jedoch wird die Definition ebenfalls vom Beobachtungswert 19 erfüllt, denn 90% der Beobachtungen liegen unter diesem Wert und 0% darüber. Gelöst wird das Problem, indem das arithmetische Mittel aus den beiden Beobachtungen gewählt wird, also \(\tilde{x}_{0,9}=\frac{17+19}{2}=18\). Für 11 Beobachtungen würde sich hingegen unmittelbar ein eindeutiges 0,9-Quantil finden lassen.
Für die Datenlage A ist somit wie folgt vorzugehen:
3.1.1 Datenlage A
Es wird mit \(p\) das gesuchte Quantil festgelegt.
Es wird \(n\cdot p\) bestimmt und geschaut, ob das Produkt ganzzahlig ist.
Es folgt:
\[\tilde{x}_p = \begin{cases} x_{([n\cdot p+1])} & \mbox{falls} \ n\cdot p \ \mbox{nicht ganzzahlig}\\ \frac{1}{2}(x_{(n\cdot p)}+x_{(n\cdot p+1)}) & \mbox{falls} \ n\cdot p \ \mbox{ganzzahlig}\\ \end{cases}\]
Dabei bedeutet die eckige Klammer, dass der Wert auf die nächste ganze Zahl abzurunden ist.
Mit der runden Klammer wird die Position in der geordneten Urliste angegeben.
Für \(p=0,9\) gilt also im Beispiel \(n\cdot p=10\cdot 0,9=9\). Da es sich um einen ganzzahligen Wert handelt, gilt weiter \[\tilde{x}_{0,9}=\frac{1}{2}(x_{(9)}+x_{(10)})=\frac{1}{2}(17+19)=18\]
Für \(p=0,75\) gilt dann im Beispiel \(n\cdot p=10\cdot 0,75=7,5\).
Da es sich hier um einen nicht ganzzahligen Wert handelt, gilt weiter
\[\tilde{x}_{0,75}=x_{([7,5+1])}=x_{(8)}=14\]
3.1.2 Datenlage B
Bei Vorliegen einer Datenlage B kann zur Bestimmung der Quantile auf die kumulierten relativen Häufigkeiten abgestellt werden. Es gilt dann
\[\tilde{x}_p = \begin{cases} x_i & \mbox{für} \ F_{i-1}<p<F_i\\ \frac{1}{2}(x_i+x_{i+1}) & \mbox{für} \ p=F_i \end{cases}\]
Falls also \(p\) mit einem \(F_i\) übereinstimmt, erfüllen zwei unterschiedliche Merkmalsausprägungen die Definition des p-Quantils und es wird wiederum das arithmetische Mittel der beiden Merkmalsausprägungen ausgewählt.
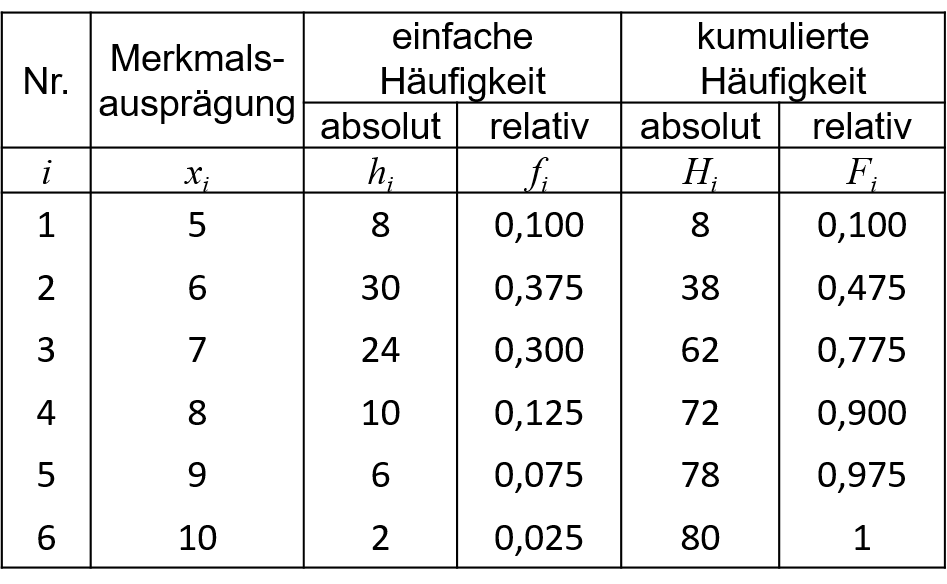
Betrachtet wird in Tabelle 3.2 noch einmal das Beispiel aus Kapitel 2.
Es sollen das 0,5 Quantil und das 0,9 Quantil bestimmt werden.
3.2: Datenlage B, Fachsemester
Zur Bestimmung des 0,5 Quantils (auch Median genannt):
\[F_2<0,5<F_3 \ \rightarrow \tilde{x}_{0,5}=7\] Die 0,5 wird mit \(F_3=0,775\) erstmalig überschritten. Somit liegt das 0,5-Quantil bei der dritten Ausprägung, also \(\tilde{x}_{0,5}=x_3=7\).
Zur Bestimmung des 0,9 Quantils:
\[0,9=F_4\ \rightarrow \tilde{x}_{0,9}=\frac{1}{2}(8+9)=8,5\] Da die 0,9 mit der kumulierten relativen Häufigkeit \(F_4\) genau übereinstimmt, erfüllen die Werte \(x_4\) und \(x_5\) die Definition des 0,9-Quantils. Es liegen also höchsten 90% der Beobachtungen unter diesen beiden Werten und höchstens 10% der Beobachtungen über diesen Werten. Somit wird das arithmetische Mittel aus \(x_4\) und \(x_5\) bestimmt.
Die ausschlaggebende Information zur Bestimmung der Quantile steckt in den kumulierten relativen Häufigkeiten \(F_i\) und somit in der Verteilungsfunktion. Abbildung 3.3 zeigt, wie sich die Quantile aus der bildlichen Darstellung der Verteilungsfunktion ablesen lassen.
Wenn \(p\) also mit einer der kumulierten relativen Häufigkeiten \(F_i\) übereinstimmt und somit \(p\) in der Grafik genau auf der Höhe einer der “Treppenstufen” liegt, erfüllen die beiden Werte am Stufenanfang und am Stufenende die Definition, so dass als Quantil das arithmetische Mittel der beiden Werte zu verwenden ist.
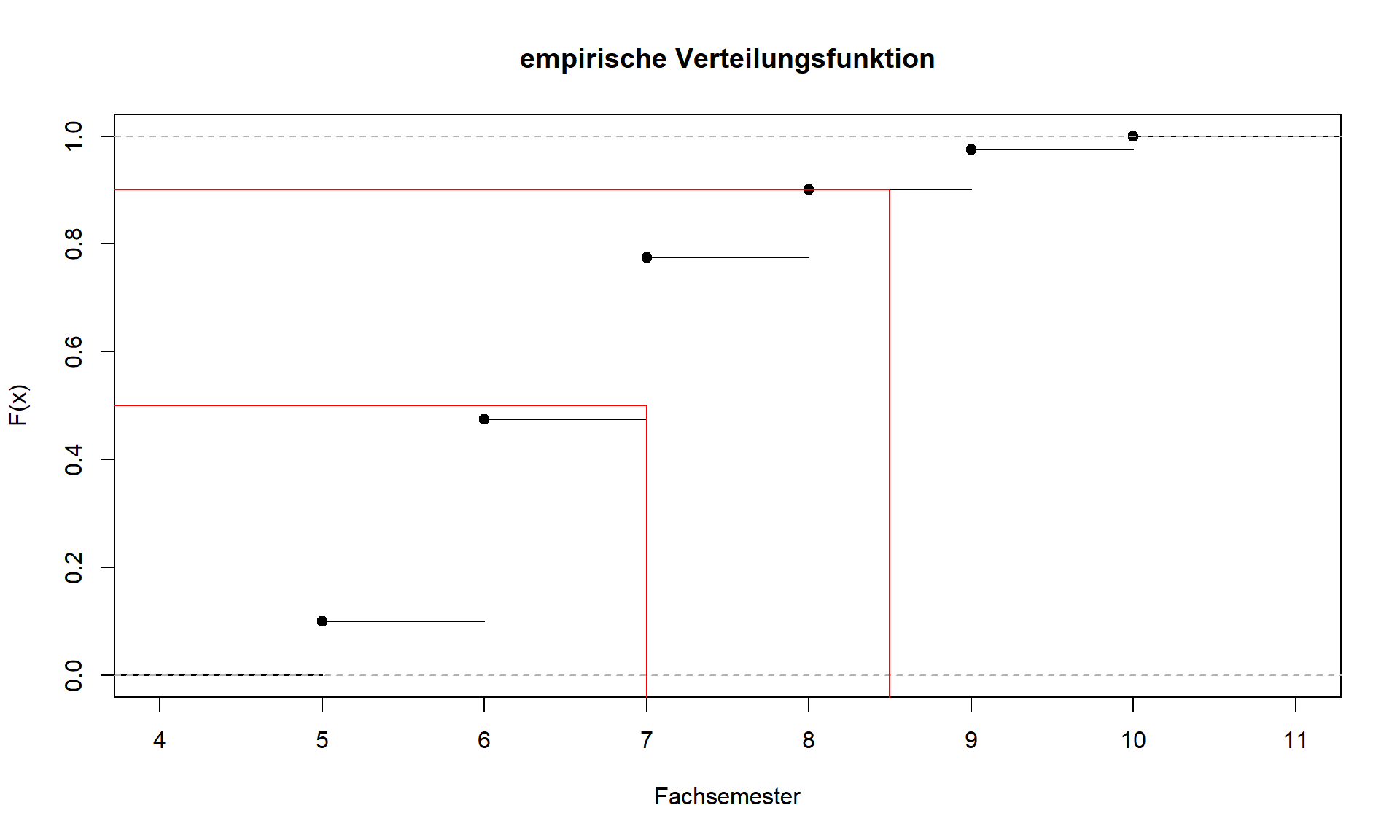
3.3: Verteilungsfunktion Merkmal Fachsemester
3.1.3 Datenlage C
Für gruppierte Daten (Datenlage C) erhält man die Quantile aus der approximierenden empirischen Verteilungsfunktion \(\hat{F}(x)\). Abbildung 3.5 zeigt, dass es zu jedem \(p\), mit \(0<p<1\), einen eindeutigen Wert \(x\) gibt, für den gilt: \(p=\hat{F}(x)\). Rot gekennzeichnet sind die Koordinaten zum 0,5-Quantil, also zum Median.
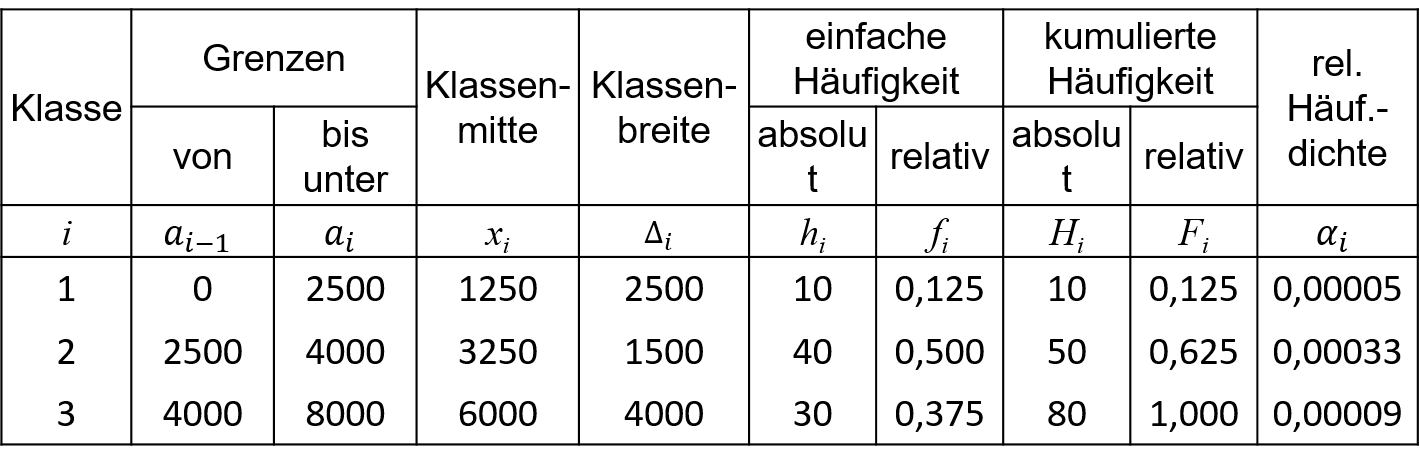
3.4: Datenlage C, monatl. Einkommen in Tsd. €
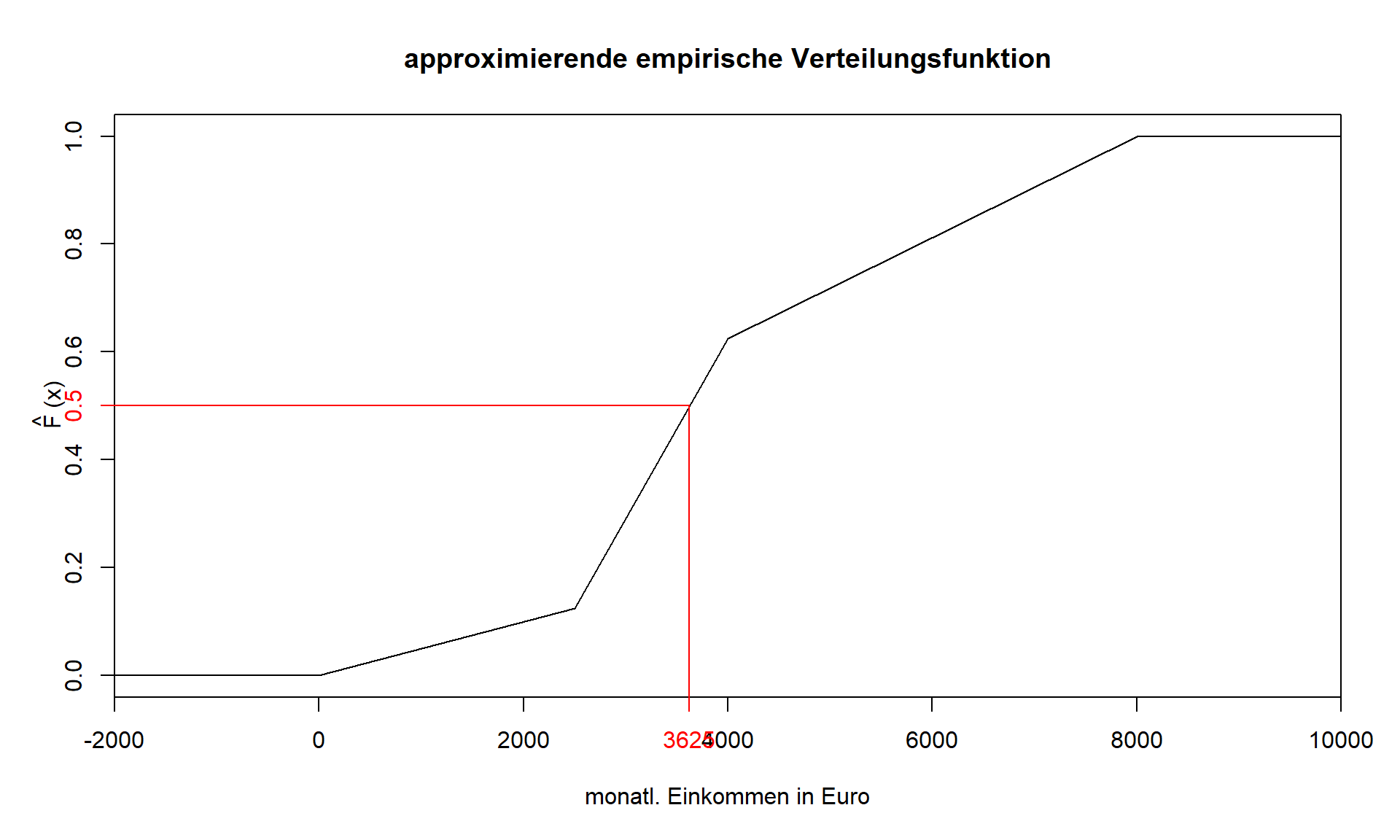
3.5: appr. emp. Verteilungsfunktion an der Stelle x=3000
Zur rechnerischen Ermittlung der Quantile ist es erforderlich, zunächst den relevanten Teil der Verteilungsfunktion zu bestimmen. Dazu wird geschaut, in welche Klasse das gesuchte Quantil fällt. Entscheidend ist also, der Vergleich von \(p\) mit den kumulierten relativen Häufigkeiten. Das Quantil fällt in die Klasse, on der \(p\) erstmalig kleiner oder gleich der kumulierten relativen Häufigkeit ist oder formal ausgedrückt: \[F_{i-1}< p\leq F_i \rightarrow \tilde{x}_p \in [a_{i-1},a_i)\] Wenn ich also zu den Klassengrenzen aus den kumulierten relativen Häufigkeiten weiß, dass 62,5% der Studierenden Einkommen bis 4000€ haben und 12,5% der Studierenden Einkommen bis 2500€ haben, dann muss mein 0,5-Quantil irgendwo dazwischen liegen. Um ein eindeutiges Ergebnis angeben zu können, betrachtet man die approximierende empirische Verteilungsfunktion für die betreffende Einkommensklasse, die in dem Beispiel für die Klasse \(i=2\) wie folgt lautet: \[\hat{F}(x)=F_{1}+\frac{f_2}{\Delta_2}(x-a_{1}) \ \mbox{für} \ \ a_{1}\leq x < a_{2} \] Nun legt man \(p\overset{!}{=}\hat{F}(x)\) fest und löst die Gleichung nach \(x\) auf. \[\underbrace{x}_{\approx\tilde{x}_p}=a_{1}+\frac{\overbrace{F(x)}^{p}-F_{1}}{f_2}\Delta_2\] Das \(\approx\) Zeichen wird verwendet, da es sich um eine Näherungslösung handelt, welche unter der Annahme der Gleichverteilung innerhalb der Klassen zustande kommt. Nachdem die Klasse \(i\) des gesuchten Quantils ermittelt wurde, gilt dann allgemein: \[\begin{align} \tilde{x}_p\approx & a_{i-1}+\frac{p-F_{i-1}}{f_i}\Delta_i\\ \mbox{bzw.}&\\ \tilde{x}_p\approx & a_{i-1}+\frac{p-F_{i-1}}{F_i-F_{i-1}}(a_i-a_{i-1}) \end{align}\]
Zur Bestimmung des 0,5-Quantils wurde festgehalten, dass dieses wegen \(F_1=0,125<0,5<F_2=0,625\) in Klasse 2 fällt.
Die Feinberechnung erfolgt dann mit
\[\tilde{x}_p\approx 2500+\frac{0,5-0,125}{0,5}1500=3625\]
3.1.4 spezielle Quantile
Besonders häufig gilt das Interesse den drei Quartilen, welche wichtige Kennzahlen zur Charakterisierung der Verteilung darstellen.
- (unteres) Quartil = 0,25-Quantil
- (mittleres) Quartil = 0,5-Quantil (Median)
- (oberes) Quartil = 0,75-Quantil
Darüber hinaus existieren noch die sogenannten Dezile. Wie der Name schon vorgibt, sind dies die 10%-,20%-… Quantile.
3.2 Mittelwerte
Mittelwerte haben zum Ziel, durch Angabe eines einzelnen, typischen Wertes für ein Merkmal, die Grundgesamtheit (statistische Masse) möglichst gut zu repräsentieren. Je nach Mittelwert werden dabei unterschiedliche Ansätze verfolgt. Dabei ist zwischen lagetypischen und rechnerischen Mittelwerten zu unterscheiden.
3.2.1 lagetypische Mittelwerte
Kennzeichnend für die lagetypischen Mittelwerte ist, dass diese über die Häufigkeitsinformationen zu den einzelnen Merkmalsausprägungen identifiziert werden können. Für diese Mittelwerte ist eine bestimmte Position (Lage) entscheidend. Die lagetypischen Mittelwerte sind sehr robust gegenüber Ausreißern in den Daten.
3.2.1.1 Modus
Als Modus wird jener Beobachtungswert bezeichnet, welcher im Datensatz am häufigsten auftritt. Insofern geht mit dem Modus eine gewisse Vorstellung von “Normalität” oder “Üblichkeit” einher. In manchen Alltagssituation, in denen man eine Auswahl hat, orientiert man sich am Modus, ohne dabei explizit an Mittelwerte zu denken. Ich bin unentschlossen und schaue mal, wofür sich die meisten anderen so entscheiden. Ich richte dann also meine Entscheidung am Modus aus.
Der Modus kann bereits ab Nominalskalenniveau und somit für jedes Skalenniveau bestimmt werden.
Datenlage A
Aus der Urliste kann der Modus nicht direkt abgelesen werden. Notwendig ist es, zu jeder Merkmalsausprägung die einfache absolute oder relative Häufigkeiten anzugeben und somit erfolgt eine Transformation der Datenlage A in die Datenlage B.
Datenlage B
Hier kann der Modus leicht über die einfachen Häufigkeiten abgelesen werden.
\[\mbox{Modus:=Merkmalsausprägung mit der größten absoluten oder relativen Häufigkeit }\]
Im Beispiel aus Tabelle 3.2 liegt der Modus also bei \(x_2=6\) Fachsemestern, da \(\underset{i}{\mbox{max}}(h_i)=h_2=30\). Anstelle auf die absoluten Häufigkeiten \(h_i\), hätte man natürlich auch auf die relativen Häufigkeiten \(f_i\) schauen können.
Datenlage C
Da bei gruppierten Daten die einzelnen Beobachtungswerte unbekannt sind, lässt sich der Modus nicht einfach über die relativen Häufigkeiten angeben. Für stetige Merkmale, bei denen alle Beobachtungswerte voneinander verschieden sind, kann ohnehin kein Modus aus den Beobachtungswerten abgeleitet werden, da jeder Wert ja nur genau einmal vertreten ist. Als Modus wird dann auf Basis der Datenlage C der Wert mit der größten Häufigkeitsdichte bestimmt. Wie aus dem Histogramm gut zu erkennen ist, verteilt sich die Häufigkeitsmasse in Form der Rechteckflächen über alle Klassen. Als Modus ist nun jener Wert mit der größten Häufigkeitsdichte zu bestimmen. In Abbildung 3.6 wird noch einmal das Histogramm zum Zahlenbeispiel aus Tabelle 3.4 betrachtet. Die modale Klasse ist also die Klasse 2 mit der größten Häufigkeitsdichte. Nun wird aber aufgrund der Gleichverteilungsannahme innerhalb der Klassen für alle Werte von 2500 bis 4000 dieselbe Häufigkeitsdichte angenommen, was durch das Histogramm anschaulich wiedergegeben wird. In vielen Fällen gibt man sich mit der Angabe der modalen Klasse zufrieden oder wählt stellvertretend die Klassenmitte aus, um einen Wert als Modus angeben zu können. Mit der Auswahl der Klassenmitte geht dann eigentlich die Annahme einher, dass sich dort die größte Häufigkeitsdichte innerhalb der modalen Klasse befindet.
Im Beispiel aus Tabelle 3.4 liegt der Modus also bei \(x_2=\frac{1}{2}(2500+4000)=3250\) Euro, da \(\underset{i}{\mbox{max}}(\alpha_i)=\alpha_2=0,00033\).
Es existieren noch weitere Verfahren zur Abschätzung des Modus, welche noch zusätzliche Informationen aus den Nachbarklassen mit berücksichtigen, aber hier nicht weiter thematisiert werden sollen.
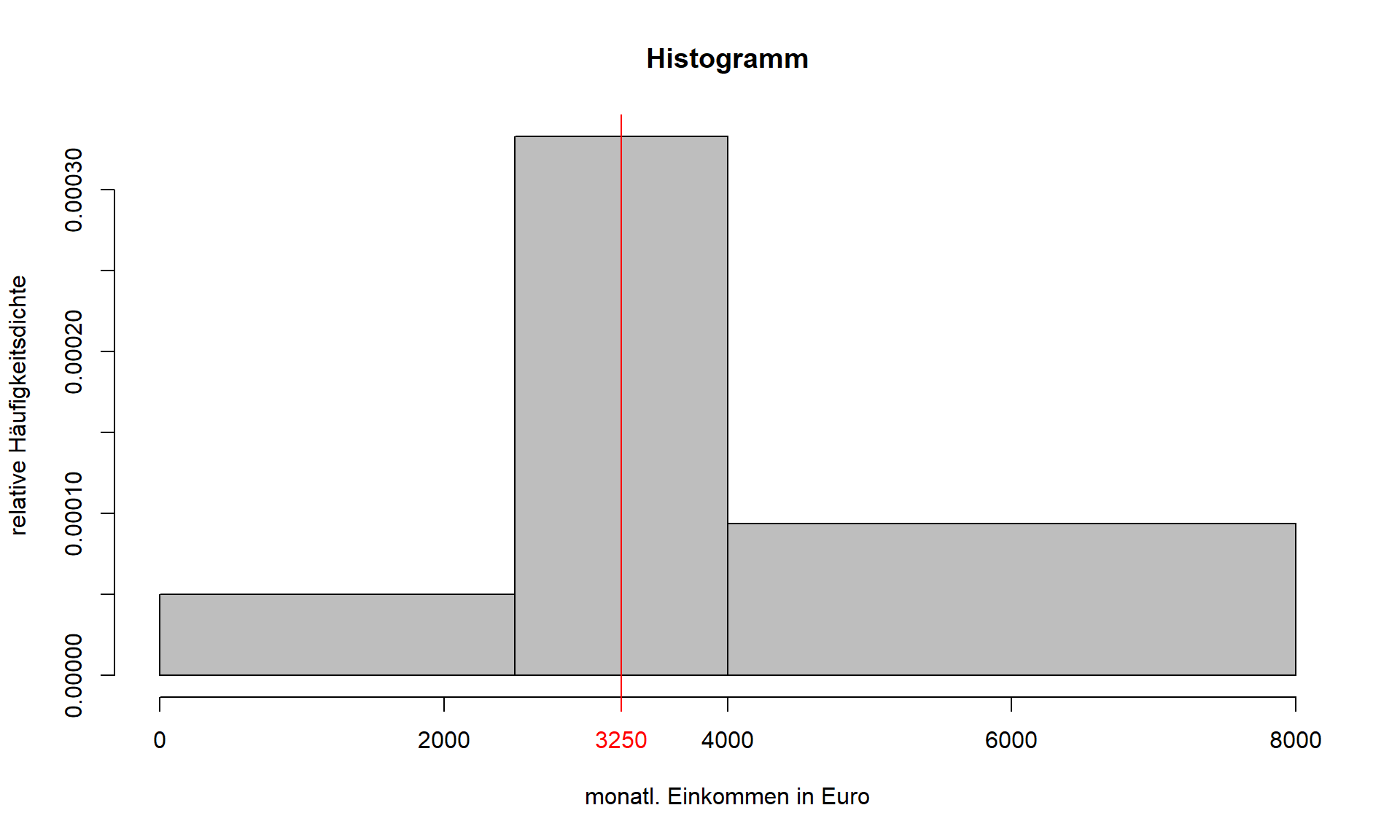
3.6: Histogramm mit Klassenmitte als Modus
3.2.1.2 Median
Als Median wird das 0,5-Quantil bezeichnet. Der Median ist also jener Wert, der die Verteilung in zwei gleich große Hälften teilt.
Bezogen auf die geordnete Urliste gibt der Median also die mittlere Position an. Der Median kann somit bereits ab Ordinalskalenniveau bestimmt werden. Gerade wenn die zentrale Tendenz einer Verteilung im Interesse steht, so kann diese gut durch den Median beschrieben werden, ohne dass es zu Verzerrungen durch starke Ausreißer an den Rändern der Verteilung kommen kann.
So ist der Median eine Kennzahl, die beispielsweise bei der Betrachtung der Merkmale “Einkommen” oder “Studiendauer in Fachsemestern” häufig dem ausreißerempfindlichen arithmetischen Mittel vorgezogen wird.
Zur genauen Bestimmung des Medians (0,5-Quantil) sei auf Kapitel 3.1 verwiesen.
3.2.2 rechnerische Mittelwerte
In die rechnerischen Mittelwerte fließen alle Merkmalsausprägungen ein, für die Beobachtungswerte vorliegen. Es werden somit mehr Informationen aus den Daten berücksichtigt, als dies bei den lagetypischen Mittelwerten der Fall ist. Dies macht sie jedoch auch anfälliger gegenüber Ausreißern. Die rechnerischen Mittelwerte werden auch als Durchschnittswerte bezeichnet.
Die Schreibweise \(\overline{x}\) macht deutlich, dass es sich um einen rechnerischen Mittelwert über die Beobachtungen handelt, welcher im Hinblick auf die vorliegende Problemstellung geeignet ist.
Erläuterungen zum Umgang mit dem Summenzeichen im folgenden Videoclip
3.2.2.1 arithmetisches Mittel
Das arithmetische Mittel ist der wohl bekannteste Mittelwert und setzt die Merkmalssumme der Grundgesamtheit ins Verhältnis zur Anzahl der Merkmalsträger \(n\) der Grundgesamtheit. \[AM=\frac{\mbox{Merkmalssumme}}{n}\] Das arithmetische Mittel kann ab Intervallskalenniveau bestimmt werden und wird für die drei Datenlagen wie folgt berechnet:
Datenlage A
Das ungewichtete arithmetische Mittel lautet: \[AM=\frac{1}{n}\sum_{i=1}^nx_i\]
Für das Beispiel aus Tabelle 3.1 gilt dann:
\[\overline{x}=\frac{1}{10}(5+7+...+19)=11,5\]
Datenlage B
Das gewichtete arithmetische Mittel lautet: \[GAM=\frac{1}{n}\sum_{i=1}^mx_i\cdot h_i\] alternativ mit relativen Gewichten: \[GAM=\sum_{i=1}^mx_i\cdot f_i\]
Für das Beispiel aus Tabelle 3.2 kann das arithmetische Mittel wie folgt berechnet werden:
\[\overline{x}=\frac{1}{80}(5\cdot 8+6\cdot 30+...+10\cdot 2)=6,775\]
Datenlage C
Unter der Annahme der Gleichverteilung innerhalb der Klassen entsprechen die mit \(x_i\) bezeichneten Klassenmitten den jeweiligen Klassendurchschnittswerten. Somit entspricht dann \(x_i \cdot h_i\) der Merkmalssumme für die Klasse \(i\). Folglich ist \(\sum_{i=1}^kx_i\cdot h_i\) die Merkmalssumme über alle \(k\) Klassen und somit über alle \(n\) Beobachtungen. Das arithmetische Mittel für die Datenlage C wird dann wie folgt berechnet:
mit den absoluten Häufigkeiten: \[GAM=\frac{1}{n}\sum_{i=1}^kx_i\cdot h_i\] mit den relative Häufigkeiten \[GAM=\sum_{i=1}^kx_i\cdot f_i\]
Für das Beispiel aus Tabelle 3.4 kann das arithmetische Mittel wie folgt berechnet werden: \[\overline{x}=\frac{1}{80}(1250\cdot 10+3250\cdot 40+6000\cdot 30)=4031,25\]
Eigenschaften des arithmetischen Mittels
Als Ersatzwerteigenschaft bezeichnet man die Tatsache, dass sich die Merkmalssumme ganz einfach bestimmen lässt, wenn \(\overline{x}\) bekannt ist. \[\overline{x}\cdot n=\sum_{i=1}^nx_i\]
Als Linearität bezeichnet man die Eigenschaft \[\overline{y}=a+b\overline{x} \ \mbox{für} \ y_i=a+bx_i\, \ a,b \in \mathbb{R}\] Das heißt, dass es für lineare Transformationen der Form \(y_i=a+bx_i\) nicht notwendig ist, alle Beobachtungen zu transformieren, wenn das Interesse \(\overline {y}\) gilt, sondern es kann \(\overline{x}\) direkt transformiert werden.
Von der Minimaleigenschaft des arithmetischen Mittels wird gesprochen, da mit \(y=\overline{x}\) die folgende Funktion \(f(y)\) minimiert wird: \[f(y)=\sum_{i=1}^n(x_i-y)^2\] Anmerkung: \(f'(y)=2(\sum_{i=1}^nx_i-ny)\overset{!}{=}0 \rightarrow y=\frac{1}{n}\sum_{i=1}^nx_i\) und \(f''(y)=-2<0 \rightarrow Minimum\)
Das arithmetische Mittel ist im Gegensatz zum Modus und Median anfällig gegenüber Ausreißern. Dies wird im folgenden Beispiel demonstriert.
3.2.2.2 harmonisches Mittel
Das harmonische Mittel setzt Verhältnisskalenniveau voraus und kommt in bestimmten Fällen bei der Mittelung von Verhältniszahlen zur Anwendung.
Eine Verhältniszahl entspricht dem Quotienten zweier Größen. Verhältniszahlen sind z.B. der Benzinpreis in € pro Liter oder der Anteil weiblicher Studierender an der Gesamtzahl der Studierenden.
Grundsätzlich wird bei der Mittelung von Verhältniszahlen das Ziel verfolgt, über die Grundgesamtheit das Verhältnis aus Zählersumme und Nennersumme zu bestimmen. Das folgende Beispiel soll dies verdeutlichen:
Ein Student betankt seinen Wagen immer für 20€. Beim ersten mal Tanken bezahlt er 1,25€/l und eine Woche später bezahlt er 1,55€/l. Welchen Preis hat er im Durchschnitt über beide Tankvorgänge bezahlt?
Das harmonische Mittel lautet für die entsprechenden Datenlagen
Datenlage A
Das ungewichtete harmonische Mittel lautet:
\[ HM = \frac{n}{\sum_{i=1}^n\frac{1}{x_i}}\]
Datenlage B
Das gewichtete harmonische Mittel lautet:
\[ GHM = \frac{n}{\sum_{i=1}^m\frac{h_i}{x_i}}\]
alternative Berechnung mit relativen Gewichten:
\[ GHM = \frac{1}{\sum_{i=1}^m\frac{f_i}{x_i}}\]
Datenlage C
Die Berechnung erfolgt, wie bei der Datenlage B, unter Verwendung der Klassenmitten \(x_i=\frac{a_{i-1}+a_i}{2}\). Das harmonische Mittel kommt für die Datenlage C aber eher selten zur Anwendung.
arithmetische Mittel vs. harmonische Mittel
Im nachfolgenden Video wird deutlich, wann welches Mittel für die Mittelung von Verhältniszahlen zur Anwendung kommt.
3.2.2.3 geometrisches Mittel
Das geometrische Mittel kommt bei zeitlich aufeinanderfolgenden Wachstumsprozessen für die Mittelung der Wachstumsfaktoren zur Anwendung und setzt Verhältnisskalenniveau voraus. Voraussetzung für eine sinnvolle Anwendung ist, dass der durch das Wachstum hinzugewonnene Teil in der Folge ebenfalls mitwächst, so wie dies etwa von Zinseszinsen bekannt ist. Die Ausgangsgröße muss nicht zwingend kontinuierlich über den Betrachtungszeitraum wachsen, sondern kann auch schrumpfen.
Datenlage A
\[GM=\left( \prod_{i=1}^nx_i\right)^{\frac{1}{n}}=\sqrt[n]{x_1\cdot x_2\cdot ...\cdot x_n}\] mit den Wachstumsfaktoren \(x_i\).
Beispiel:
Angenommen ein Wertpapier wird über einen Zeitraum von drei Jahren gehalten und erzielt in den ersten beiden Jahren eine Rendite von 2% und im dritten Jahr eine Rendite von 3%, so wird die jahresdurchschnittliche Rendite auf Basis der Wachstumsfaktoren ermittelt. Für die Jahre eins und zwei liegen die Wachstumsfaktoren demnach bei 1,02 und für das dritte Jahr liegt der Wachstumsfaktor bei 1,03.
Es ist dann zunächst der Gesamtwachstumsfaktor zu ermitteln, mit \(1,02\cdot 1,02\cdot 1,03\). Der jahresdurchschnittliche Wachstumsfaktor entspricht dann
\[\sqrt[3]{ 1,02\cdot 1,02\cdot 1,03}=1,0233\]
Die jahresdurchschnittliche Rendite liegt demnach bei 2,33%.
Datenlage B
\[GGM=\left( \prod_{i=1}^m x_i^{h_i}\right)^{\frac{1}{n}}\] mit den Wachstumsfaktoren \(x_i\).
Fortsetzung Beispiel:
Da der Wachstumsfaktor 1,02 zweimal auftritt und der Wachstumsfaktor 1,03 einmal, hätte man unter Berücksichtigung der Häufigkeiten auch notieren können:
\[\sqrt[2+1]{1,02^2\cdot 1,03^1}=1,0233\]
Datenlage C
Die Berechnung erfolgt, wie bei der Datenlage B, unter Verwendung der Klassenmitten \(x_i=\frac{a_{i-1}+a_i}{2}\). Das geometrische Mittel kommt für die Datenlage C aber eher selten zur Anwendung.
Beziehung zum arithmetischen Mittel
Der Logarithmus von \(GM\) bzw. \(GGM\) entspricht dem \(AM\) bzw. \(GAM\) der logarithmierten Werte.
\[log(GM)=\frac{1}{n}\sum_{i=1}^nlog(x_i)\] bzw. \[log(GGM)=\frac{1}{n}\sum_{i=1}^mh_i\cdot log(x_i)\] Dieser Zusammenhang ist für die formale Darstellung von ökonomischen Modellen von Bedeutung, da sich so auch multiplikative Zusammenhänge durch lineare Modelle abbilden lassen, was in vielen Fällen vorteilhaft ist.
3.2.3 allgemeine Aussagen
Sofern keine Variation in den Beobachtungswerten vorhanden ist, also für jeden Merkamlsträger der gleiche Beobachtungswert vorliegt, also \(x_i=c \ \forall \ i \in \ \{1,...,n\}\), gilt:
\[\mbox{Modus}=\mbox{Median}=\mbox{AM}=\mbox{HM}=\mbox{GM}\]
Aus den Mittelwerten Modus, Median und arithmetische Mittel lassen sich zudem Aussagen über den Typ der Häufigkeitsverteilung ableiten. Die Lageregeln von Fechner besagen für:
\[\mbox{Modus}<\mbox{Median}<\mbox{AM} \rightarrow \mbox{linkssteile Verteilung}\]
\[\mbox{Modus}>\mbox{Median}>\mbox{AM} \rightarrow \mbox{rechtssteile Verteilung}\]
\[\mbox{Modus}=\mbox{Median}=\mbox{AM} \rightarrow \mbox{symmetrische Verteilung}\]
In der praktischen Beurteilung spricht man auch von einer symmetrischen Verteilung, wenn die drei Mittelwerte sehr nahe beieinander liegen: \[\mbox{Modus} \approx \mbox{Median}\approx\mbox{AM} \rightarrow \mbox{symmetrische Verteilung}\]
Abbildung 3.7 zeigt die linkssteile Verteilung der monatlichen Haushaltsnettoeinkommen in Deutschland für das Jahr 2013.
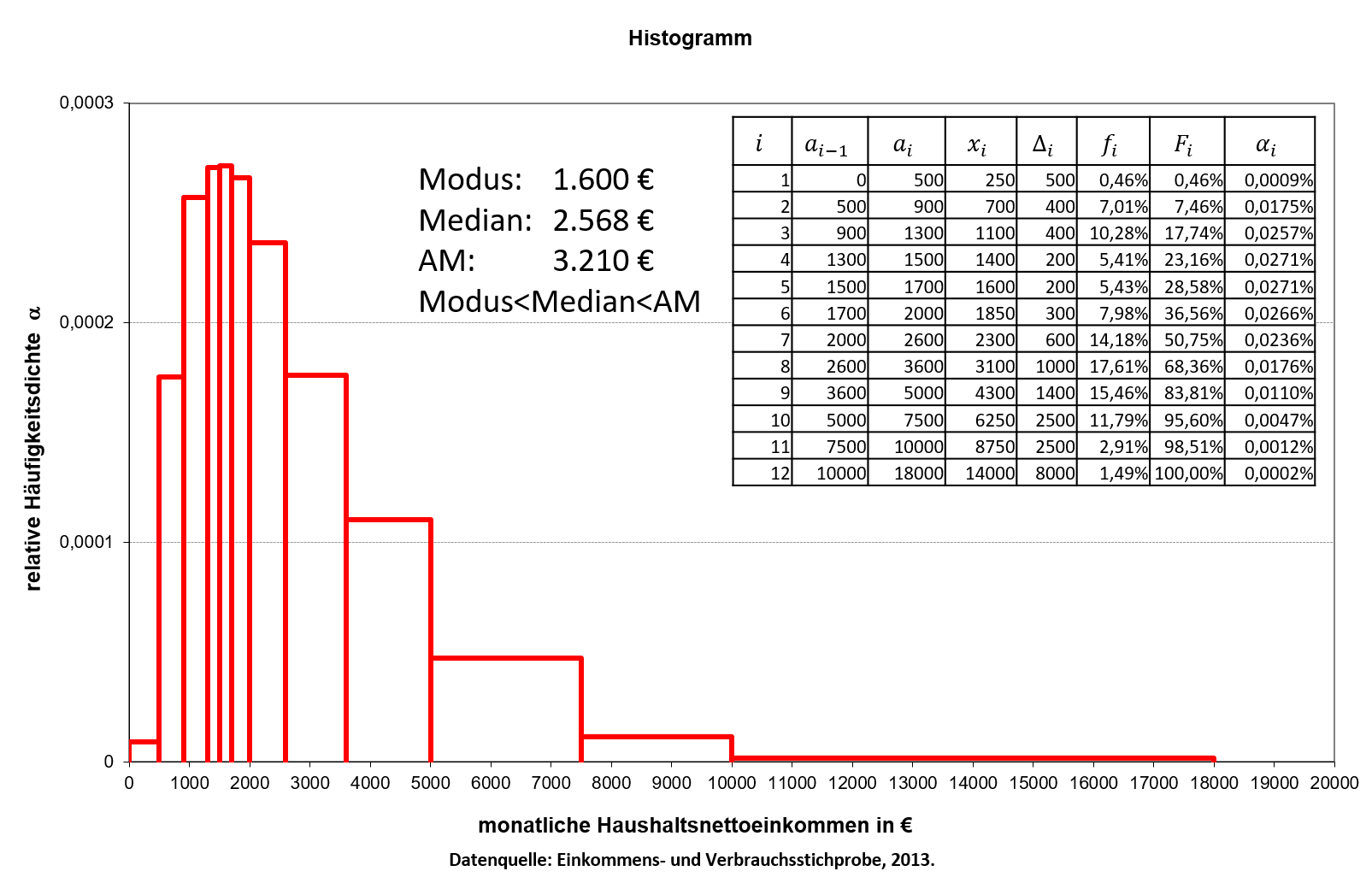
3.7: linkssteile Verteilung
Im folgenden Video werden Modus, Median und arithmetisches Mittel bezugnehmend auf die Datenlage C aus Abbildung 3.7 berechnet.