Kapitel 10 Wahrscheinlichkeitsrechnung

Die Wahrscheinlichkeitsrechnung befasst sich mit Zufallsvorgängen, also mit Vorgängen, bei denen bekannt ist, welche Ergebnisse eintreten können. Es ist aber nicht mit Gewissheit vorhersagbar, welches der möglichen Ergebnisse am Ende eintreten wird.
Welches Ergebnis bei einem solchen Vorgang im Einzelfall eintritt, hängt vom Zufall ab. Der Begriff Zufall besagt, dass die systematischen Einflussfaktoren unbekannt oder zumindest in ihrer Wirkung nicht abschätzbar sind. Ob ein Phänomen als Zufallsvorgang interpretiert wird, hängt also letztlich von der Wahrnehmung bzw. dem Kenntnisstand des Beobachters ab.
Zufallsvorgänge sind für alle Tatbestände von Bedeutung, welche nicht mit Sicherheit bestimmt oder vorhergesagt werden können und stellen somit einen wichtigen Gegenstand bei der Bildung und mathematischen Formalisierung ökonomischer Modelle dar. So wird etwa im Rahmen der Prognose des Bruttoinlandsproduktes von den Wirtschaftsforschungsinstituten nicht nur bloß ein Zahlenwert, sondern ein Prognoseintervall mit zugehöriger Wahrscheinlichkeit angegeben. Ähnlich verhält es sich mit der Wettervorhersage, welche modellbasiert eine bestimmte Wetterlage prognostiziert, zu der oft auch eine Eintrittswahrscheinlichkeit angegeben wird. Selbst diese geschätzte Eintrittswahrscheinlichkeit ist ein mit Unsicherheit behafteter Zahlenwert.

10.1 klassische Wahrscheinlichkeitsrechnung

Die klassische Wahrscheinlichkeitsrechnung steht im Zusammenhang mit dem Mathematiker Laplace.
Als Laplace-Experiment bezeichnet man Zufallsvorgänge mit endlich vielen und gleichwahrscheinlichen Resultaten. Laplace-Experimente findet man bei Glücksspielen, wie z.B. dem Roulette oder dem Werfen eines Würfels oder einer Münze, vor.

Es wird nun die folgende Notationsvereinbarung getroffen:

• \(G\) bezeichnet die Menge aller möglichen Resultate eines Zufallsvorgangs. Für den Würfelwurf gilt: \(G=\{1,2,3,4,5,6\}\)
• Mit weiteren Großbuchstaben werden bestimmte Ereignisse im Rahmen des Zufallsvorgangs bezeichnet. Z.B. kann das Ereignis, die Augenzahl beim Würfeln ist gerade, mit \(A\) bezeichnet werden.
• \(G_A\) bezeichnet dann die Menge aller Resultate im Sinne von \(A\), welche auch als günstige Resultate bezüglich \(A\) bezeichnet werden. Es gilt somit im Beispiel: \(G_A=\{2,4,6\}\)
• Mit \(n[G]\) wird dann die Anzahl der Elemente in der Menge \(G\) bezeichnet. Es gilt im Beispiel also: \(n[G]=6\) und \(n[G_A]=3\).

Die Wahrscheinlichkeit für das Eintreten des Ereignis \(A\), also \(W(A)\) lässt sich dann im Rahmen eines Laplace-Experiments wie folgt berechnen: \[W(A)=\frac{n[G_A]}{n[G]}=\frac{Anzahl \ günstige \ Resultate}{Anzahl \ mögliche \ Resultate}\]

Die Wahrscheinlichkeit für eine gerade Augenzahl beim Würfeln lautet also: \(W(A)=\frac{3}{6}=\frac{1}{2}\).
Für jedes beliebige Ereignis \(A\) muss gelten: \(0\leq W(A)\leq 1\).
Falls \(W(A)=0\), so wird \(A\) als unmögliches Ereignis bezeichnet.
Falls \(W(A)=1\), so wird \(A\) als sicheres Ereignis bezeichnet.

mehrere Ereignisse

Betrachtet man neben dem Ereignis \(A\) noch ein weiteres Ereignis \(B\), z.B. “Augenzahl \(\geq 4\)”, so können neben den Wahrscheinlichkeiten \(W(A)\) und \(W(B)\) die folgenden Wahrscheinlichkeiten von Interesse sein:

• \(W(A\cap B)\) bezeichnet die Wahrscheinlichkeit für das Eintreten der Ereignisse \(A\) und \(B\).
• \(W(A \cup B)\) bezeichnet die Wahrscheinlichkeit für das Eintreten von \(A\) oder \(B\), wobei dies kein ausschließendes oder ist. D.h. auch \(A\cap B\) ist in \(A \cup B\) enthalten.

Zur Veranschaulichung betrachten wir die Abbildung 10.1. Im linken Mengendiagramm weisen die Ereignisse \(A\) und \(B\) keine Schnittmenge auf. Im rechten Mengendiagramm existiert eine Schnittmenge. Ereignisse ohne Schnittmenge werden als disjunkt bezeichnet.
Die Wahrscheinlichkeit für \(W(A \cup B)\) kann auch wie folgt berechnet werden: \[W(A \cup B)=W(A)+W(B)-W(A\cap B)\] Hintergrund ist der, dass in den Wahrscheinlichkeiten \(W(A)\) und \(W(B)\) jeweils die Resultate der Schnittmenge berücksichtigt und somit doppelt gezählt werden. Damit die Schnittmenge aber nur einfach berücksichtigt wird, zieht man die Wahrscheinlichkeit für \(W(A\cap B)\) am Ende ab. \[W(A \cup B)=\frac{n[G_{A\cup B}]}{n[G]}=\frac{n[G_A]+n[G_B]-n[G_{A\cap B}]}{n[G]}=W(A)+W(B)-W(A\cap B)\]

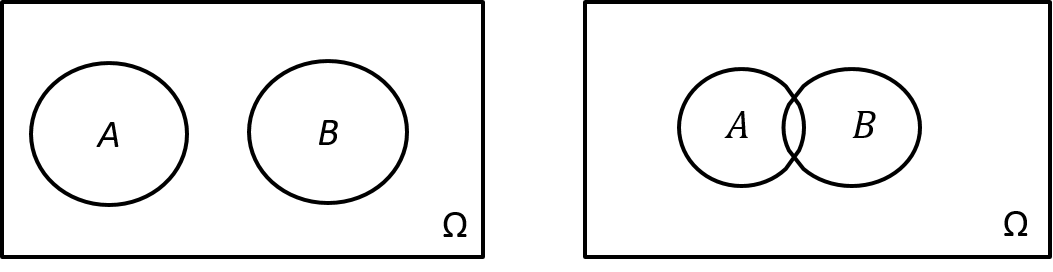
10.1: Mengendiagramm, Ereignisse mit und ohne Schnittmenge

Wir greifen erneut das Beispiel des Würfelwurfs auf mit den Ereignissen:

• \(A:=\) Augenzahl gerade
• \(B:=\) Augenzahl \(\geq 4\)

Es folgt:

• \(G_{A}=\{2,4,6\}\)
• \(G_B=\{4,5,6\}\)
• \(G_{A\cap B}=\{4,6\}\)
• \(G_{A\cup B}=\{2,4,5,6\}\)

Folgende Wahrscheinlichkeiten können dann nach der klassischen Wahrscheinlichkeitsrechnung ermittelt werden:

• \(W(A)=\frac{3}{6}=\frac{1}{2}\)
• \(W(B)=\frac{3}{6}=\frac{1}{2}\)
• \(W(A\cap B)=\frac{2}{6}=\frac{1}{3}\)
• \(W(A\cup B)=\frac{4}{6}=\frac{2}{3}\) alternativ \(W(A\cup B)=W(A)+W(B)-W(A\cap B)=\frac{1}{2}+\frac{1}{2}-\frac{1}{3}=\frac{2}{3}\)

Häufig sind auch die Gegenereignisse (Komplementärereignisse) von Interesse. Formal werden die Gegenereignisse mit einem Überstrich geschrieben. Mit \(\overline{A}\) wird also das Gegenereignis zu \(A\) bezeichnet. \(\overline{A}\) bedeutet im Beispiel: “Die Augenzahl ist ungerade”
Die Menge der Resultate zu \(\overline{A}\) kann als Differenzmenge aus \(G\) und \(G_A\) bestimmt werden: \[G_{\overline{A}}=G \backslash G_A\] Im Beispiel gilt dann für die Menge aus allen Augenzahlen abzüglich der geraden Augenzahlen: \[G_{\overline{A}}=G \backslash G_A=\{1,2,3,4,5,6\}\backslash \{2,4,6\}=\{1,3,5\}\] Die Wahrscheinlichkeit für \(\overline{A}\) als Gegenereignis zu \(A\) kann dann einfach bestimmt werden als: \[W \left(\overline{A} \right)=1-W\left( A \right) \]

10.2 Kombinatorik

Die Kombinatorik beschäftigt sich mit der Anzahl der Möglichkeiten von Zusammenstellungen bzw. Anordnungen von Elementen aus festgelegten Mengen. Die Kombinatorik ist grundlegend zur Bestimmung der Anzahl günstiger und möglicher Resultate für Laplace-Experimente.

10.2.1 Permutationen

Unter einer Permutation versteht man eine Anordung von \(n\) Elementen.
Zunächst sei davon auszugehen, dass alle Elemente unterscheidbar seien, z.B. mit unterschiedlichen Zahlen nummeriert worden sind.

Die Zahl der voneinander unterscheidbaren Permutationen kann für ausschließlich voneinander unterscheidbare Elemente bestimmt werden mit: \[\begin{align*} 0!&=1\\ 1!&=1\\ 2!&=1 \cdot 2\\ n!&=1\cdot2\cdot...\cdot n,\mbox{ mit } n\geq 3\\ \end{align*}\]

Beispiel:
Die \(n=3\) Elemente werden nummeriert mit 1,2,3 und sind somit unterscheidbar. Die Permutationen lauten: \[3!=1\cdot 2\cdot 3=6\]

\((1,2,3)\)	\((1,3,2)\)	\((2,1,3)\)
\((2,3,1)\)	\((3,1,2)\)	\((3,2,1)\)

Bei \(n\) Elementen, von denen je \(n_1, n_2, . . . , n_k\) untereinander gleich sind, beträgt die Anzahl der Permutationen:

\[\frac{n!}{n_1!\cdot...\cdot n_k!}\]

Beispiel:
Die \(n=3\) Elemente werden nummeriert mit 1,2,2. Es gilt hier:
\(n=3, \ n_1=1,\ n_2=2\)
Die Permutationen lauten: \[\frac{3!}{1!\cdot 2!}=3\]

\((1,2,2)\)

\((2,1,2)\)

\((2,2,1)\)

Aufgabe:
Ein Fußballspiel endet unentschieden mit dem Ergebnis 2:2.
Wie viele unterschiedliche Spielverläufe hinsichtlich der Zwischenergebnisse kommen für dieses Endergebnis in Betracht?
Die Lösung findet sich im folgenden Video:

10.2.2 Urnenmodell

Bei der klassischen Wahrscheinlichkeitsrechnung geht es stets darum, die Anzahl der im Rahmen des Zufallsexperimentes möglichen und die Anzahl der hinsichtlich eines Ereignisses günstigen Resultate zu bestimmen. Dabei ist es häufig hilfreich, die Anzahl der günstigen und möglichen Resultate mit kombinatorischen Ansätzen zu ermitteln.
Zur Veranschaulichung dient das willkürliche Ziehen von Elementen aus einer Urne mit \(n\) unterscheidbaren Elementen. Die Fragestellung hier lautet: “Wie viele unterschiedliche Resultate können sich beim Ziehen aus der Urne einstellen?”

Prinzipiell ist zunächst zu unterscheiden, ob gezogene Resultate mit gleichen, aber verschieden angeordneten Elementen als gleiche oder unterschiedliche Resultate verstanden werden. Resultate, bei denen die Reihenfolge unterschieden wird, werden als Variationen bezeichnet. Falls die Reihenfolge egal ist und nur die Mengen wichtig sind, spricht man von Kombinationen.
Als weiteres Unterscheidungsmerkmal dient das Ziehen mit Zurücklegen und ohne Zurücklegen.

Im Folgenden werden nun \(k\) Elemente aus der Urne mit \(n\) Gesamtelementen gezogen.
Wie bereits erwähnt, sind die Kriterien Ziehen mit/ohne Reihenfolge und Ziehen mit/ohne Zurücklegen entscheidend. Die folgende Tabelle veranschaulicht die zu thematisierenden kombinatorischen Formeln:

	Variationen (mit Reihenfolge)	Kombinationen (ohne Reihenfolge)
mit Zurücklegen	\(n^k\)	\(\binom{n+k-1}{k}=\frac{(n+k-1)!}{k!\cdot (n-1)!}\)
ohne Zurücklegen	\(\frac{n!}{(n-k)!}\)	\(\binom{n}{k}=\frac{n!}{k!\cdot (n-k)!}\)

Im folgenden Video wird zu jeder der vier kombinatorischen Formeln ein Beispiel mit \(k=2\) Zügen aus \(n=3\) Elementen aufgezeigt.

Besonderheit beim Ziehen mit Zurücklegen ohne Berücksichtigung der Reihenfolge

Voraussetzung bei der Bestimmung von Laplace-Wahrscheinlichkeiten ist, dass alle möglichen Resultate des Zufallsvorgangs als gleichwahrscheinlich angesehen werden können.
Dies ist beim Ziehen mit Zurücklegen, ohne Berücksichtigung der Reihenfolge (Kombinationen) jedoch nicht der Fall.
Betrachtet man beim Ziehen von \(k=2\) aus \(n=3\) unterscheidbaren Elementen die 6 möglichen Kombinationen mit Zurücklegen, so ist festzuhalten, dass im durchgeführten Urnenexperiment die Resultate aus Zeile 1 doppelt so wahrscheinlich sind, wie die Resultate aus Zeile 2. Die geschweiften Mengenklammern zeigen im Folgenden an, dass keine Unterscheidung der Reihenfolge erfolgt.

Zeile 1	\(\{1,2\}\)	\(\{1,3\}\)	\(\{2,3\}\)
Zeile 2	\(\{1,1\}\)	\(\{2,2\}\)	\(\{3,3\}\)

Grundsätzlich sind beim betrachteten Urnenexperiment mit Zurücklegen 9 gleichwahrscheinliche Resultate möglich, deren Eintrittswahrscheinlichkeiten somit jeweils bei \(\frac{1}{9}\) liegen. Diese lauten:

Zeile A	\((1,2)\)	\((1,3)\)	\((2,3)\)
Zeile B	\((2,1)\)	\((3,1)\)	\((3,2)\)
Zeile C	\((1,1)\)	\((2,2)\)	\((3,3)\)

Durch die Nichtberücksichtigung der Reihenfolge lassen sich dann spaltenweise die Elemente aus den Zeilen A und B als jeweils identische Menge schreiben.
Die Eintrittswahrscheinlichkeit von \((1,2)\) und \((2,1)\) beträgt jeweils \(\frac{1}{9}\) und die Eintrittswahrscheinlichkeit von \(\{1,2\}\) beträgt somit \(\frac{2}{9}\).
Man kann sich daher grundsätzlich merken, dass die Bestimmung von Wahrscheinlichkeiten für ein Ziehen mit Zurücklegen und ohne Berücksichtigung der Reihenfolge nicht auf der Grundlage der kombinatorischen Formel\(\binom{n+k-1}{k}\) zu erfolgen hat. Stattdessen berechnet man Wahrscheinlichkeiten für Ereignisse beim Ziehen mit Zurücklegen immer auf Basis der Formel mit Berücksichtigung der Reihenfolge, also \(n^k\) unter Einbezug aller Reihenfolgen für die günstigen Resultate.
Beispiel:
Wie groß ist die Wahrscheinlichkeit beim Ziehen mit Zurücklegen von \(k=3\) Elementen aus den Zahlen 1,2,3,4 die Zahlen 1,2 und 3 zu ziehen?
Lösung:
Es existieren \(4^3\) mögliche Resultate beim Ziehen mit Zurücklegen und mit Berücksichtigung der Reihenfolge.
Es existieren \(3!=6\) günstige Resultate, denn es sollen nur die Zahlen 1,2 und 3 gezogen werden, ohne dass es auf die Reihenfolge ankommt. Da \(3!=6\) Permutationen für die Zahlen 1,2,3 möglich sind und das Ereignis lautet “Es sollen die Zahlen 1,2,3 gezogen werden”, sind alle 6 möglichen Permutationen als Günstige zu berücksichtigen. \[W("Zahlen \ 1, \ 2 \ und \ 3")=\frac{6}{4^3}=\frac{3}{32}\]

Ziehen ohne Zurücklegen Beim Ziehen ohne Zurücklegen tritt dieses Problem nicht auf. Betrachtet man die 3 möglichen Kombinationen beim Ziehen aus \(n=3\) Elementen mit \(k=2\) Zügen ohne Zurücklegen, so ist festzustellen, dass diese aus der spaltenweisen Zusammenfassung der im Folgenden abgebildeten Variationen ohne Zurücklegen resultieren:

Zeile 1	\((1,2)\)	\((1,3)\)	\((2,3)\)
Zeile 2	\((2,1)\)	\((3,1)\)	\((3,2)\)

Die 6 oben abgebildeten Resultate sind alle gleichwahrscheinlich mit einer Wahrscheinlichkeit von jeweils 1/6. Die Betrachtung ohne Berücksichtigung der Reihenfolge führt dann zu den spaltenweise identischen Mengen, deren Wahrscheinlichkeiten alle bei 1/3 liegen, also gleichwahrscheinlich sind:

Zeile 1

\(\{1,2\}\)

\(\{1,3\}\)

\(\{2,3\}\)

Beispiel:
Beim Lottospiel (6 aus 49 ohne Superzahl) soll die Wahrscheinlichkeit für 4 Richtige berechnet werden.
Die Lösung findet sich im folgenden Video:

Übungsaufgaben
Lösen Sie die folgenden 4 Aufgabenstellungen anhand des Urnenmodells:

• Für einen Bundesligaspieltag werden jeweils für die Heimmannschaft die Ausgänge Sieg, Niederlage oder Unentschieden getippt. Wie viele Möglichkeiten gibt es beim Tipp von zwei Spielpaarungen?
  

• Bei einem 100m Lauf mit 8 Teilnehmern werden die Gold-, Silber- und Bronzemedaillengewinner getippt. Wie viele Möglichkeiten gibt es?
  

• Bei einem 100m Lauf mit 8 Teilnehmern werden die drei Bestplatzierten getippt, ohne eine Zuordnung der Medaillen. Wie viele Möglichkeiten gibt es?
  

• 3 Schülerinnen und Schüler stellen sich als Klassensprecher zur Wahl. Wie viele unterschiedliche Wahlergebnisse sind möglich, wenn 20 Schülerinnen und Schüler zur Wahl gehen und alle Stimmzettel gültig sind?