3.2 Methods

We developed a decision analytic model to estimate the health-economic consequences of whole blood pathogen inactivation in Ghana from a healthcare payer perspective. We considered seven adverse events, including viral TTIs (HIV, HCV, HBV), bacterial TTIs (syphilis, bacterial sepsis), malaria, and febrile non-hemolytic transfusion reactions (FNHTRs), a non-infectious adverse event. We estimated the cost per adverse event averted and the budget impact of whole blood PI, and we assessed uncertainty through deterministic and probabilistic sensitivity analysis. The model was programmed in R. All data and code are available in a public repository [Will create citation before submitting].

3.2.1 Risk reduction model structure

Our two-armed decision tree compared the costs and consequences of status quo blood safety interventions to those of the status quo plus whole blood PI. The status quo was to test all donations using HIV-Ab, HBV-Ag, HBsAg, Anti-HCV Ab, and syphilis serologic tests [95]. All parameters values for the risk reduction model are shown in Table 3.1 <[94–106]>, and mathematical calculations are provided in the Section A of the online supplement. For each input parameter, we estimated a range of likely values for deterministic sensitivity analysis and assigned a distribution for probabilistic sensitivity analysis. We used beta distributions when estimates were based on counts for a binary outcome or when the parameter source used a beta distribution. Otherwise we sampled each parameter from a PERT distribution. For all outcomes, we reported the expected value from the base case scenario and a 95% uncertainty interval based on the 2.5th and 97.5th quantiles of results from 10,000 iterations of probabilistic sensitivity analysis.

We assumed that each whole blood donation would be transfused to a single recipient, and we assumed that if one recipient experienced multiple adverse events from a single transfusion then any adverse event costs would be additive. For each of the six TTIs, the baseline (without PI) number of clinically meaningful adverse events was calculated from the annual number of whole blood donations collected nationally, the percent of collected donations not transfused (wastage), the estimated residual risk among donors after TTI screening, and the risk of clinical outcome (i.e., likelihood that transfusion of an infectious unit results in clinically relevant disease). For FNHTR, a non-infectious adverse event, the baseline rate of clinically relevant adverse events per recipient was extrapolated from local data and prior studies, and the per-donation risk of FNHTR was derived by multiplying the per-recipient rate by the estimated average number of whole blood units transfused per recipient. We assumed some recipients were not at risk of clinical outcomes due to factors such as prior malaria infection, HBV vaccination, and existing HIV infection (see Table 3.1). For each adverse event, we divided by a fold risk-reduction factor to estimate the number of adverse events when using whole blood PI. These risk-reduction factors were based on clinical trials where available (malaria, FNHTR) and otherwise sourced from prior modeling studies.

3.2.2 Cost of adverse events

We estimated the average health care spending associated with each transfusion-related adverse using a micro-costing approach. For most adverse events, authors with relevant clinical experience at the Komfo Anokye Teaching Hospital (KATH) in Kumasi, Ghana, estimated the costs and utilization patterns for resources used to treat each adverse event. For HIV, we assumed infections that had not yet progressed to AIDS would be detected in an outpatient clinic and used empirical costing estimates from a recent study of healthcare costs for patients initiating antiviral therapy (AVT) [107]. We treated FNHTR, malaria, syphilis, and sepsis as acute infections and assumed all costs were incurred within a year of transfusion. We treated HIV, HBV, and HCV as chronic viral infections and used Markov models to estimate lifetime healthcare costs. Supplemental Table 8.1 <[107]> contains estimates and uncertainty ranges for all micro-costing parameters, and Supplemental Table 8.2 contains the calculations used for the four acute adverse events and for each disease state of the chronic viral infections.

For each chronic viral infection, we modeled a pediatric cohort (age 5 at transfusion) and an adult cohort (age 40 at transfusion). Models captured the disease natural history, treatment uptake, and treatment effectiveness. We used a one-year cycle length, discounted future costs at 3% annually, and used the cycle tree method to correct for discretization error [108]. The probability of dying from another cause in all disease states was based on the 2016 age-specific death rate indicator in the World Health Organization Global Health Observatory data repository [109]. All other transition probabilities and their sources are listed in Supplemental Table 8.3 <[110–113]>. A schematic of the Markov model for each disease is shown in Figure 3.1. The supplement also contains schematics for the transition matrix for each chronic adverse event (Supplementary Figures 8.1, 8.2, and 8.3) and Markov trace plots of the proportion of transfusion recipients in each disease state over time (Supplementary Figures 8.4, 8.5, and 8.6).

For HCV, our natural history model and treatment efficacy estimates were based on a health economic model developed for The Gambia [111], and transitions into treatment were estimated based on the authors’ clinical experience. We assumed a small portion of infections would be detected during the acute phase in the first year and receive antiviral therapy (AVT); otherwise, recipients would have subclinical acute infections. We assumed a portion of subclinical infections in the chronic, compensated cirrhosis, and decompensated cirrhosis would be detected each year, and those patients would receive AVT. We assumed AVT would clear most HCV infections, but some patients would experience treatment failure and be subject to disease progression while receiving monitoring and care.

For HBV, our natural history model and treatment efficacy estimates were based on a health economic model developed for South Africa [112]. We assumed a small fraction of acute infections would be detected and receive monitoring and care during the first year, but most infections would be subclinical during the acute phase. Subclinical infections in the immune reactive, compensated cirrhosis, or decompensated cirrhosis states had an annual probability of clinical detection, at which point AVT would be begun. subclinical patients in the chronic HBeAg- phase also had an annual probability of detection. Those patients would transition to receiving monitoring and care without AVT but could be started on AVT due to clinical indications such as a spike in viral load. We assumed patients on AVT would not progress to later disease states and would continue with AVT and monitoring for their lifetimes. For those on AVT with cirrhosis, a small annual risk of developing hepatocellular carcinoma remained.

For HIV, we constructed a natural history model and calibrated the annual probability of progression to AIDS, death from HIV, and death from AIDS to a longitudinal study of HIV progression from Uganda (Figure 8.7) [113]. We assumed patients who initiated AVT before progressing to AIDS would continue with treatment for the remainder of their lives and have a normal life expectancy. Annual costs for those who initiated AVT before progressing to AIDS were based on an empirical study conducted in HIV clinics in Ghana that found that on average, medical expenses were highest in the year of AVT initaition and tapered off over three years [107]. For patients who initiated AVT after progressing to AIDS, we assumed they would be diagnosed and initiate ART during a hospitalization for AIDS complications and therefore incur substantially higher costs in the first two years as compared to those initiating ART with HIV. Co-authors with relevant clinical experience estimated those costs. We also assumed those initiating ART with AIDS would have a higher risk of dying for the first two years of AVT, but after two years on ART, we assumed surviving AIDS patients would have recovered their CD4 counts and have the same annual costs and risk of death as any other AVT patient. We estimated the annual probability of initiating AVT based on HIV progression based on the authors’ clinical experience.

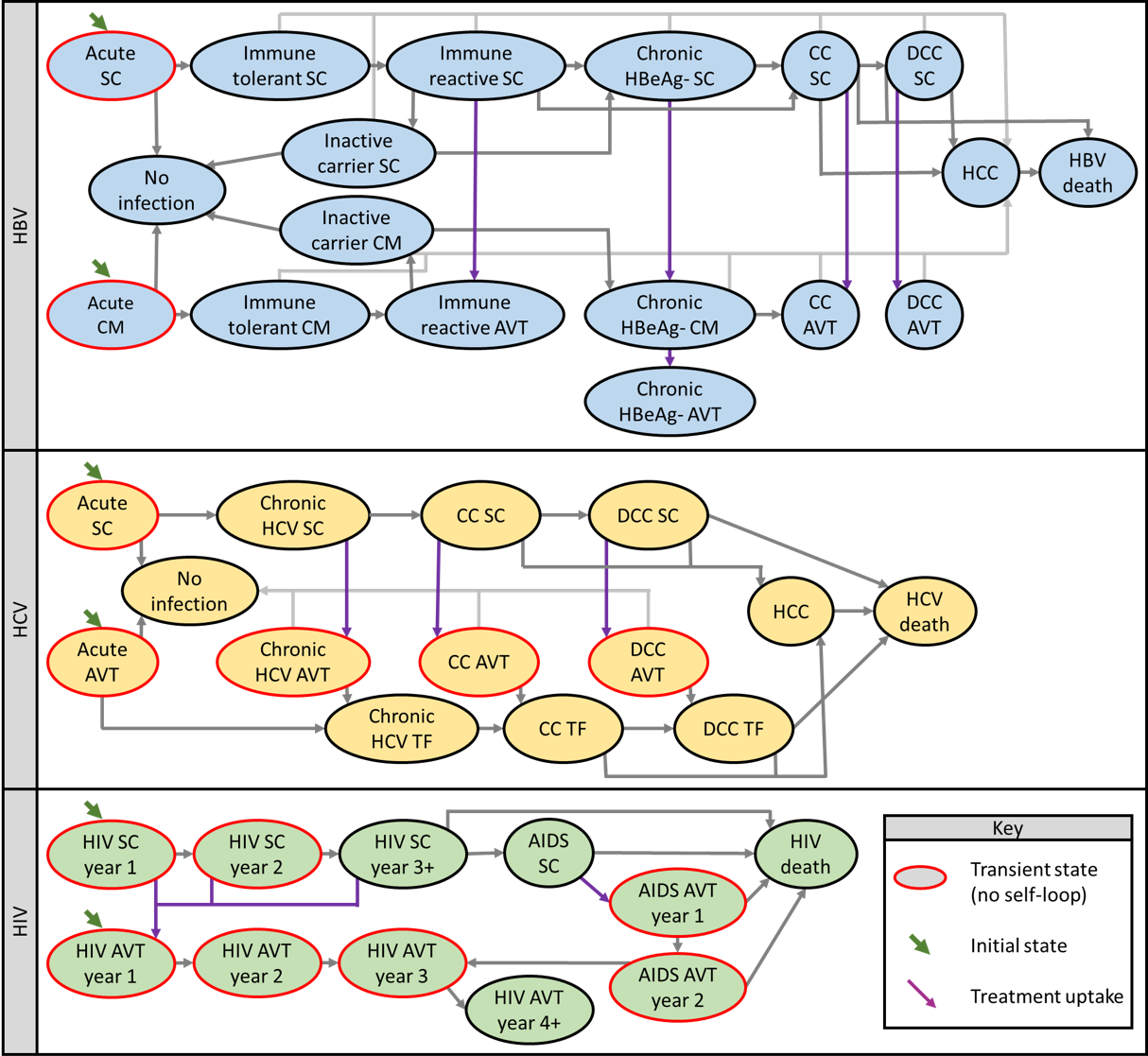
Figure 3.1: Schematics for Markov models used to estimate net-present lifetime costs for chronic viral infections.

Death from other causes possible from any disease state (not shown). Abbreviations AVT, antiviral therapy, CC, compensated cirrhosis, CM, clinical monitored, DCC, decompensated cirrhosis, HCC, hepatocellular carcinoma, HBV, hepatitis B, HCV, hepatitis C, HIV, human immunodeficiency virus, TF, treatment failure, SC, subclinical.

3.2.3 Scenario analysis

In a scenario analysis, we incorporated costs due to secondary infections by assuming each recipient infected with HIV, HBV, or HCV infects one other person of the same age during the first year.