6.4 Simplificación de estados

Dos estados son equivalentes cuando para cualquier secuencia de entradas la máquina evoluciona de la misma manera:

  • Pasa por los mismos estados
  • Presenta la misma salida en todo momento

En la tabla de transición de estados, la caracterización de estados equivalentes se corresponde con aquellas filas que presentan los mismos valores en todas las celdas. Todos aquellos estados equivalentes pueden simplificarse en uno solo.

Por ejemplo, en la Tabla 6.5, se puede simplificar la fila 2 y la 3, fusionando m1 con m2 (y dejando, por ejemplo, m1):

Tabla 6.5: Ejemplo de tabla de estados equivalentes
m \ x1x2 00 01 11 10
m0 m0,0 m0,1 m1,0 m2,1
m1 m0,1 m1,0 m1,1 m1,0
m2 m0,1 m1,0 m1,1 m1,0

En el ejemplo, si se elimina el estado m2, habría que modificar el resto de filas en las que apareciera m2 y cambiarlo por m1. Por tanto la Tabla 6.5 se transformaría en la Tabla 6.6:

Tabla 6.6: Ejemplo de tabla de estados equivalentes simplificada.
m \ x1x2 00 01 11 10
m0 m0,0 m0,1 m1,0 m1,1
m1 m0,1 m1,0 m1,1 m1,0

La simplificación de estados no es obligatoria realizarla. Hay veces que al simplificar estados se pierde el significado físico del estado (i.e. cilindro expandido, puerta abierta, etc.). Y, consecuentemente, se puede elegir no simplicar al máximo, manteniendo los estados elegidos inicialmente. Es una decisión del diseñador. La simplificación es interesante realizarla cuando se tienen recursos técnicos limitados (por ejemplo, memoria). También es interesante para dilucidar si el sistema es combinacional o secuencial.

6.4.1 Método de simplificación

Aunque las filas de la tabla de transición de estados no sean idénticas, también es posible reducir el número de estados fusionándolas. Esto se puede hacer cuando tengamos combinaciones de entradas que “no importan” (nos dan igual bien porque no se pueden dar o porque es indiferente hacia donde evolucione el sistema), representadas por una X y llamadas también indefinidas o imposibles (en inglés se denominan “don’t care”). Se pueden fusionar filas que tengan en sus columnas:

  • El mismo estado.
  • Condiciones de “no importa” (X).

Incluso se pueden fusionar filas que tengan salidas distintas. En este caso estaríamos creando una máquina de Mealy. Es decir, si partimos de una máquina de Moore, en la que la salida está definida por cada estado, y fusionamos filas con salidas iguales, mantenemos la máquina de Moore. Si, por el contrario, fusionamos filas con salidas diferentes, estaríamos pasando a una máquina de Mealy29.

Vamos a verlo con unos ejemplos.

6.4.2 Ejemplo de simplificación con salidas iguales

Se pide realizar un automatismo para el control de un cilindro de doble efecto con una electroválvula 5/2 monoestable. Se dispone de un pulsador P y un sensor de posición S, que detecta la expansión máxima del cilindro. Al pulsar P se realizará un ciclo completo de expansión/compresión del cilindro. Para la compresión del cilindro P debe estar desactivado.

En primer lugar identificamos las entradas {P, S} y las salidas {A1}.

A continuación dibujamos el diagrama de estados (Fig. 6.9). Partimos de un estado de reposo m1. Si pulsamos P pasaremos a m2, activando la salida y expandiendo el cilindro. En m2 hay dos opciones. La primera es que soltemos P, pasando a m3 (y el cilindro se sigue expandiendo). La segunda, que no soltemos P y que el cilindro llegue a su expansión máxima (m4). Estando en m3, cuando el cilindro llegue a su expansión máxima, se activará S y pasaremos al estado m5. En m4, cuando soltemos P, también pasaremos a m5. En m5 el cilindro se está comprimiendo y cuando se desactive S se pasará al estado m1, en el que el cilindro se terminará de comprimir y permanecerá comprimido.

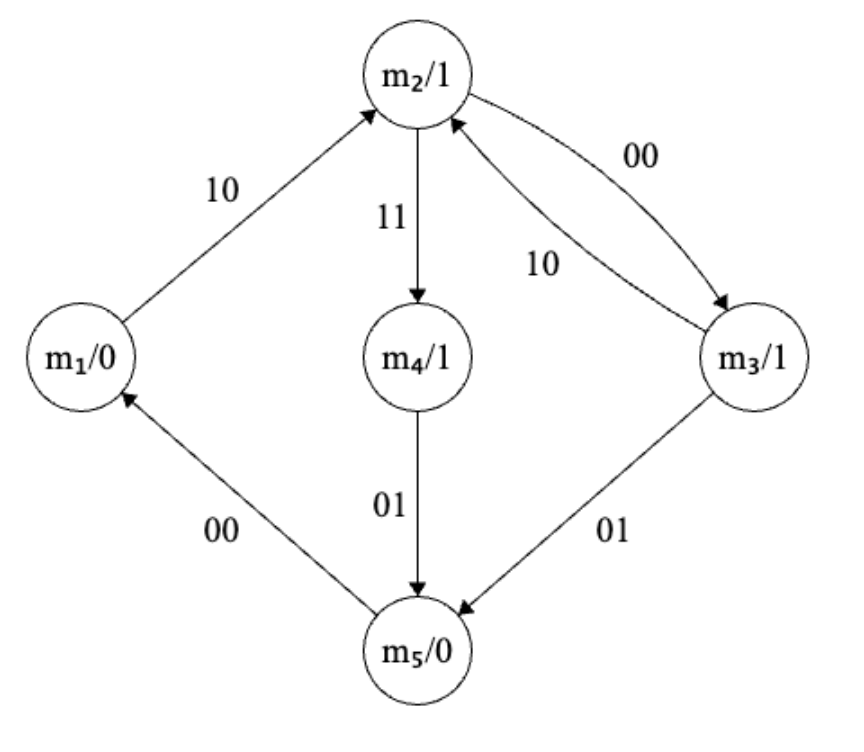
Diagrama de estado

Figura 6.9: Diagrama de estado

A partir del diagrama obtenemos la tabla de transición de estados.

Tabla 6.7: Tabla de estados
m \ PS 00 01 11 10 Salida(A1)
m1 m1 x x m2 0
m2 m3 x m4 m2 1
m3 m3 m5 x m2 1
m4 x m5 m4 x 1
m5 m1 m5 m4 x 0

Vemos que se indican varios estados imposibles (X). Estos estados surgen porque, o bien el estado no se puede dar (por motivos físicos o mecánicos), o bien porque la funcionalidad del sistema no lo permite. En este caso consideramos que las dos entradas no pueden cambiar a la vez. Siempre habrá una que cambie un poco antes que la otra.

Procedemos a fusionar filas (estados). A simple vista vemos que podemos fusionar las filas 1 y 5, y por otro lados las filas 2, 3, y 4. Nos quedaría la tabla simplificada (Tabla 6.8), en la que renombramos los estados: m1 y m5 pasan a ser ma. Y m2, m3 y m4 pasan a ser mb.

Tabla 6.8: Tabla de estados simplificada
m \ PS 00 01 11 10 Salida(A1)
ma m1 m5 m4 m2 0
mb m3 m5 m4 m2 1

Renombrando los estados obtenemos:

Tabla 6.9: Tabla de estados simplificada con memoria.
m \ PS 00 01 11 10 Salida(A1)
ma ma ma mb mb 0
mb mb ma mb mb 1

A partir de aquí, para obtener las ecuaciones del sistema podemos utilizar dos métodos: ecuaciones de activación/retención o tabla de verdad.

6.4.2.1 Resolución mediante ecuaciones de activación y retención

A partir de la Tabla 6.9 podemos obtener fácilmente las ecuaciones de los estados:

\[m_a(k+1) = m_b(k) · \overline{P}·S + m_a(k)·\overline{m_b(k+1)}\] \[m_b(k+1) = m_a(k) · P + m_b(k)·\overline{m_a(k+1)}\] Y de la salida:

\[ A1(k) = m_b(k) \]

6.4.2.2 Resolución mediante tabla de verdad

Al tener sólo dos estados, que hemos llamado ma y mb, podemos codificarlos con sólo un bit de memoria.

Tabla 6.10: Tabla de estados simplificada con memoria.
m \ PS 00 01 11 10 Salida(A1) Memoria
ma ma ma mb mb 0 0
mb mb ma mb mb 1 1

También podemos hacer la tabla de verdad, con dos entradas, P y S, una memoria y una salida. mk=0 corresponde a ma, y mk=1 corresponde a mb. Para cada fila de la tabla de verdad 6.11, se obtienen los valores a partir de la tabla de estados 6.10, mediante la fila que indica el estado (ma o mb) y la columna que indican PS.

Tabla 6.11: Tabla de verdad.
P S mk mk+1 A1k
0 0 0 0 0
0 0 1 1 1
0 1 0 0 0
0 1 1 0 1
1 0 0 1 0
1 0 1 1 1
1 1 0 1 0
1 1 1 1 1

Finalmente podemos obtener las ecuaciones. Se ve claramente (porque las columnas son idénticas) que:

\[A1(k) = m(k)\] Mediante un diagrama de Karnaugh (Fig. 6.10) podemos obtener la ecuación del estado siguiente:

\[m(k+1) = P + m(k) · \overline{S}\]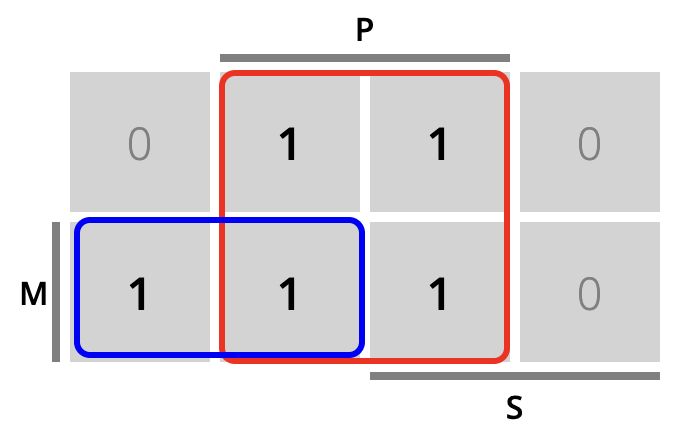
Diagrama de estado

Figura 6.10: Diagrama de estado

Nota.- Se puede observar que las ecuaciones de transición de estados son equivalentes a las del apartado 6.4.2.1, y que éste último está empleando dos variables internas en lugar de una. No siendo mínimo, tiene la ventaja de que son estados con semántica física y de uso habitual en los modelos reales de control.

6.4.3 Ejemplo de simplificación con salidas distintas

Se pide diseñar un sistema de control de señalización de un cruce de vías. Cuando un tren es detectado por la vía A, se activa el semáforo en la vía B, RB. En el caso de detectar un tren por la vía B, el semáforo RA se encenderá.

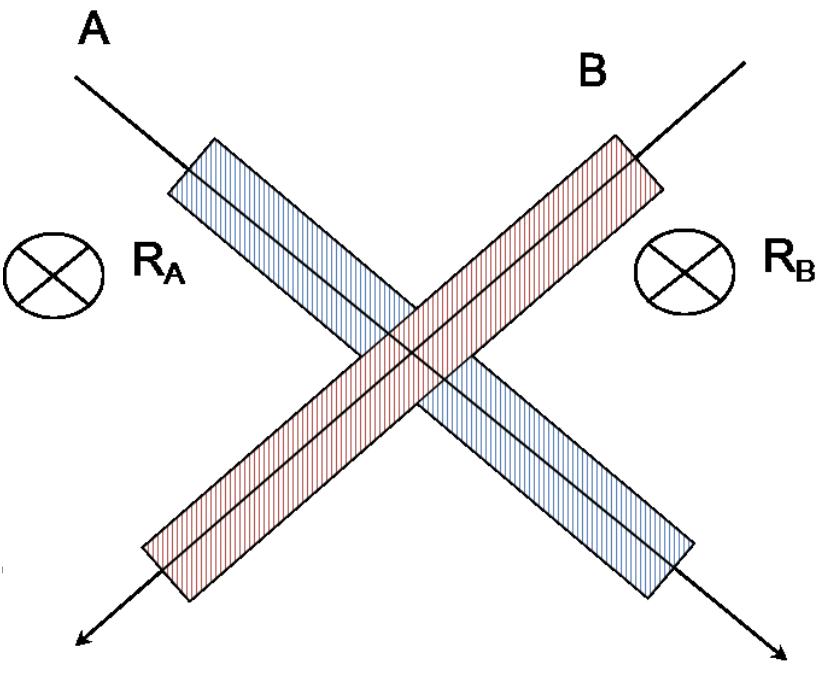
Cruce de trenes

Figura 6.11: Cruce de trenes

En primer lugar, realizamos el diagrama de estados (Fig. 6.12). La semántica de los estados es la siguiente: m0 es el estado de reposo. m1 indica que se ha detectado un tren por la vía A, por lo que se activa el semáforo RB. De forma análoga, m2 indica que se ha detectado un tren por la vía B, por lo que se activa el semáforo RA. m3 indica que, habiéndose detectado un tren en la vía A, también se detecta un tren por la vía B, teniendo prioridad el tren de la via A (semáforo RB activo). De forma análoga, m4 indica que, habiéndose detectado un tren en la vía B, también se detecta un tren por la vía A, teniendo prioridad el tren de la via B (semáforo RA activo). En los arcos se indican las entradas (AB) y en los estados las salidas RARB.

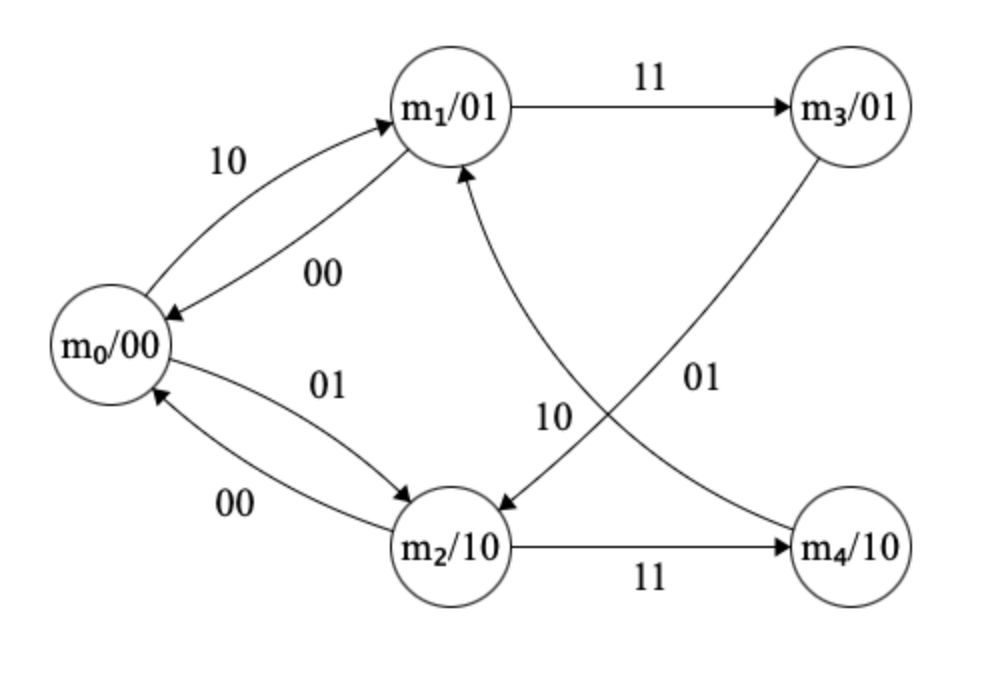
Diagrama de estados de cruce de trenes

Figura 6.12: Diagrama de estados de cruce de trenes

A continuación, la tabla de transición de estados:

Tabla 6.12: Tabla de transición de estados.
m \ AB 00 01 11 10 Salidas(RA RB)
m0 m0 m2 x m1 0 0
m1 m0 x m3 m1 0 1
m2 m0 m2 m4 x 1 0
m3 x m2 m3 x 0 1
m4 x x m4 m1 1 0

Ahora procedemos a simplificar la tabla. Al igual que antes, podemos ir por dos caminos.

6.4.3.1 Resolución por ecuaciones de activación y retención

Si no necesitamos hacer una simplificación máxima, podemos fusionar las filas que tengas las mismas salidas. En este caso, fusionamos m1 con m3 (llamado m13), y m2 con m4 (llamado m24).

Tabla 6.13: Tabla de transición de estados.
m \ AB 00 01 11 10 Salidas(RA RB)
m0 m0 m24 x m13 0 0
m13 m0 m24 m13 m13 0 1
m24 m0 m24 m24 m13 1 0

A partir de aquí obtenemos las ecuaciones de activación y retención:

\[m_0(k+1) = (m_{13}(k) + m_{24}(k)) · \overline{A}·\overline{B} + m_0(k)·(\overline{m_{13}(k+1)} + \overline{m_{24}(k+1)})\] \[m_{13}(k+1) = m_{0}(k) · A + m_{24}(k) · A · \overline{B} + m_{13}(k) · (\overline{m_0(k+1)}) + \overline{m_{24}(k+1)})\] \[m_{24}(k+1) = m_{0}(k) · B + m_{13}(k) · \overline{A} · B + m_{24}(k)·(\overline{m_0(k+1)}) + \overline{m_{13}(k+1)})\]

Observando la tabla detenidamente también se podría obtener:

\[m_0(k+1) = \overline{A}·\overline{B}\]

Y las de las salidas:

\[Ra(k) = m_{24}(k)\] \[Rb(k) = m_{13}(k)\]

6.4.3.2 Resolución por tabla de verdad

Ahora vamos a buscar la simplificación máxima. En este caso vamos a fusionar estados no equivalentes, es decir, fusionamos filas aunque no tengan las mismas salidas. Fusionamos los estado 0, 1 y 3 por un lado (ma), y 2 y 4 por otro (mb). La nueva tabla quedaría:

Tabla 6.14: Tabla de transición de estados simplificada (sin salidas).
m \ AB 00 01 11 10 Memoria
ma ma mb ma ma 0
mb ma mb mb ma 1

Para representar los nuevos estados nos basta con una memoria (1 bit).Ya no podemos indicar las salidas porque no dependen exclusivamente del estado. Aunque podemos expresarla como una máquina de Mealy:

Tabla 6.15: Tabla de transición de estados simplificada con salidas (Mealy).
m \ AB 00 01 11 10 Memoria
ma ma,00 mb,10 ma,01 ma,01 0
mb ma,00 mb,10 mb,10 ma,01 1

Por tanto, la tabla de verdad quedaría:

Tabla 6.16: Tabla de verdad.
A B mk mk+1 RAk RBk
0 0 0 0 0 0
0 0 1 0 0 0
0 1 0 1 1 0
0 1 1 1 1 0
1 0 0 0 0 1
1 0 1 0 0 1
1 1 0 0 0 1
1 1 1 1 1 0

Y las ecuaciones quedarían de la siguiente forma. RA se obtiene de forma inmendiata:

\[R_A(k) = m(k+1)\] El resto se pueden obtener mediante diagrama de Karnaugh:

\[m(k+1) = B · (\overline{A} + m(k))\] \[R_B(k) = A · (\overline{B} + \overline{m(k)})\]

6.4.4 Ejemplo de simplificación combinacional

Se desea realizar un sistema de control de calidad para una fábrica. Se dispone de:

  • una cinta transportadora que se mueve mediante un motor, accionado mediante una señal R (‘0’: paro, ‘1’: marcha).

  • una cámara que detecta si alguna pieza está defectuosa, generando una señal S que vale ‘1’ cuando la pieza está defectuosa y ‘0’ en caso contrario.

  • un interruptor I (si está en ON genera un ‘1’; si está en OFF genera un ‘0’)

  • un cilindro neumático que se controla mediante una válvula neumática y una señal A.

Cuando se pone el interruptor en ON, el motor se pone en marcha y empiezan a llegar piezas. Si la cámara detecta una pieza defectuosa, la cinta se para y se activa el cilindro para expulsar la pieza de la cinta. Cuando la cámara no detecta la pieza se vuelve a poner en marcha. Si el interruptor se pone en OFF la cinta se para (siempre que no haya una pieza defectuosa bajo la cámara).

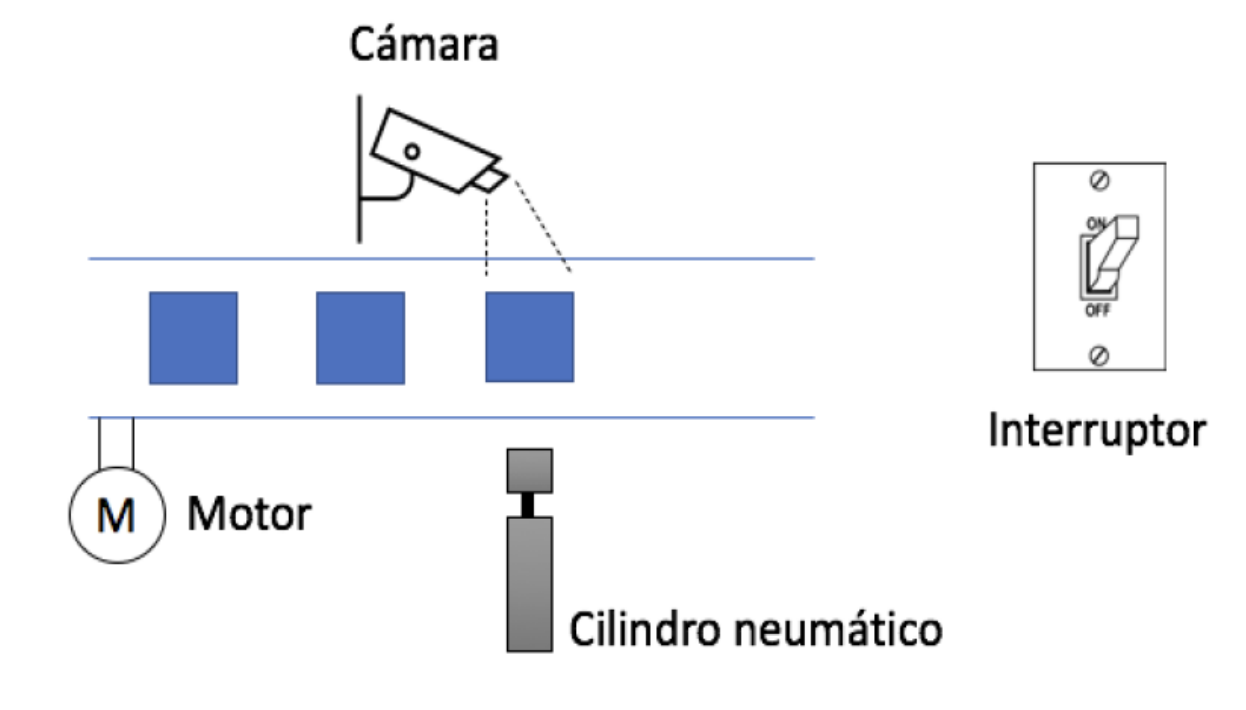
Ejemplo de cámara de detección de piezas defectuosas.

Figura 6.13: Ejemplo de cámara de detección de piezas defectuosas.

En primer lugar dibujamos el diagrama de estados, empezando por el estado de reposo m1.

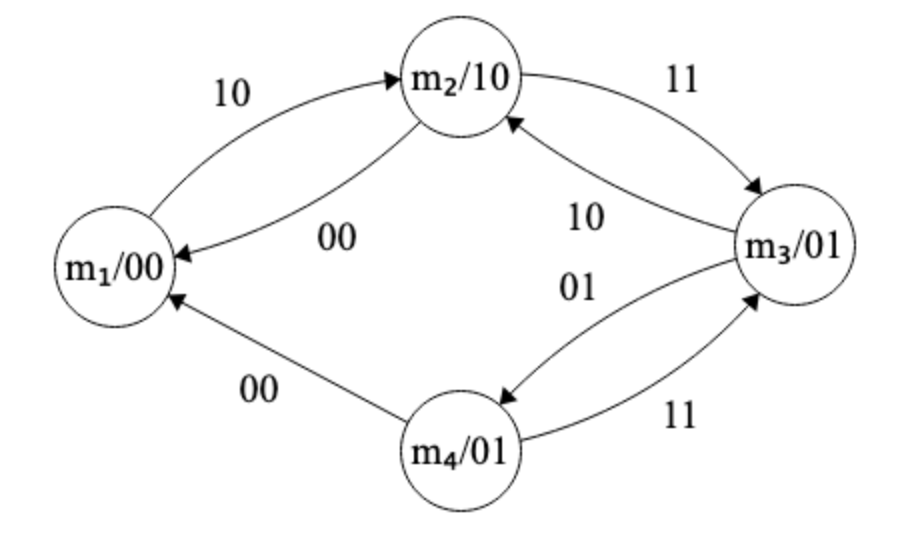
Diagrama de estados del ejemplo de cámara de detección de piezas defectuosas.

Figura 6.14: Diagrama de estados del ejemplo de cámara de detección de piezas defectuosas.

Pasamos a la tabla de transición de estados:

Tabla 6.17: Tabla de transición de estados.
m \ IS 00 01 11 10 Salidas(R A)
m1 m1 m4 x m2 0 0
m2 m1 x m3 m2 1 0
m3 x m4 m3 m2 0 1
m4 m1 m4 m3 x 0 1

Vemos que podemos fusionar todas las filas, obteniendo:

Tabla 6.18: Tabla de transición de estados simplificada.
m \ IS 00 01 11 10
m1 m1 m4 m3 m2

La podemos expresar con la salidas:

Tabla 6.19: Tabla de transición de estados simplificada (Mealy).
m \ IS 00 01 11 10
m1 m1,00 m4,01 m3,01 m2,10

Se trata, por tanto, de un sistema combinacional.

La tabla de verdad quedaría (no hace falta indicar estados porque no hay, es combinacional):

Tabla 6.20: Tabla de verdad.
I S R A
0 0 0 0
0 1 0 1
1 0 1 0
1 1 0 1

Y las ecuaciones:

\[ R = I · \overline{S}\] \[ A = S \]

Ejercicio.- A continuación se plantean dos cuestiones extra:

  • Implementación de las ecuaciones mediante diagrama de escalera
  • Indicar qué tipo de cilindro neumático y de válvula neumática utilizaría.

Solucion

Implementación mediante diagrama de escalera

La implementación mediante diagrama de escalera es muy sencilla:

Ejercicio de control de calidad: diagrama de escalera

Figura 6.15: Ejercicio de control de calidad: diagrama de escalera

Puede comprobar su funcionamiento en https://www.plcfiddle.com/.

Indicar qué tipo de cilindro neumático y de válvula neumática utilizaría

Dado que se debe controlar con una sola señal, el cilindro debe ser de simple efecto controlado por una válvula 3/2.

Referencias

Huffman, D. A., The synthesis of sequential switching circuits, Journal of the Franklin Institute, vol. 257, n.º 3, pp. 161-90, a partir de https://www.sciencedirect.com/science/article/pii/0016003254905748, 1954. DOI: https://doi.org/10.1016/0016-0032(54)90574-8
Moreno, E. G., Automatización de procesos industriales, Alfaomega, 2001.

  1. Este método se puede encontrar en la bibliografía como método de Huffman (Huffman, 1954) o método de la tabla de fases (Moreno, 2001).↩︎