3.3 Mapa de Karnaugh

Un mapa de Karnaugh24 (también conocido como tabla de Karnaugh o diagrama de Veitch) es un diagrama utilizado para la simplificación de funciones algebraicas en forma canónica. A partir de la tabla de Karnaugh se puede obtener una forma canónica mínima (con el mínimo número de términos). En este texto emplearemos indistintamente los términos “mapa” y “tabla” de Karnaugh.

Nota.- Observe que siempre existirán dos formas canónicas mínimas, una DNF y otra CNF.

La tabla de Karnaugh consiste en una representación bidimensional de la función que se quiere simplificar. Si la función viene expresada como una tabla de verdad, entonces la tabla de Karnaugh puede verse como una forma alternativa de representación 2D. Puesto que la tabla de verdad de una función de n variables posee 2n filas, la tabla de Karnaugh correspondiente debe poseer también 2n celdas. La construcción de la tabla de Karnaugh pasa por codificar cada celda en código binario reflejado (o código Gray) de manera que celdas adyacentes tengan un código que difiere en un solo dígito.

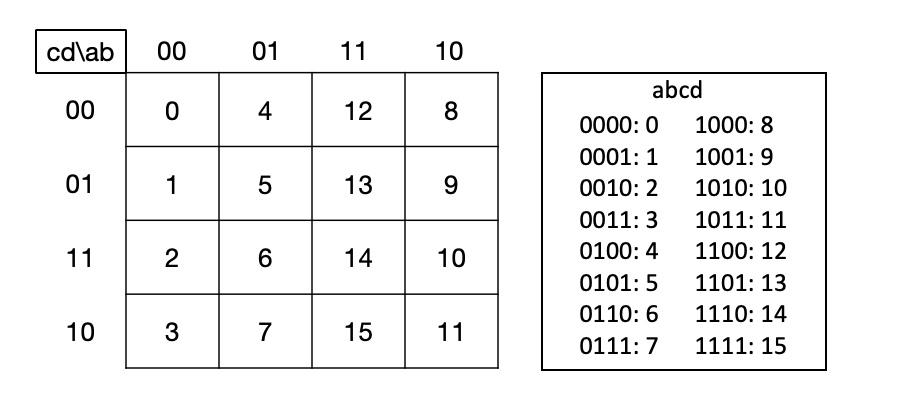
Descripción del mapa de Karnaugh

Figura 3.1: Descripción del mapa de Karnaugh

En la Fig. 3.1 puede verse un ejemplo de codificación Gray para el caso de funciones lógicas de 4 variables. Cada variable lógica (A, B, C, D en la figura) se corresponde con un bit del código Gray.

En la práctica, no es necesario explicitar el código de cada celda; basta con expresar las cabeceras de las filas y columnas en código Gray (el código de la celda se construye combinando la fila y columna correspondiente), según se desprende de la figura.

Definida la codificación Gray para la tabla, las celdas se rellenan asignando el valor ‘1’ para el caso que exista el término canónico correspondiente en la función objeto de análisis, y el valor ‘0’ en caso contrario. Si la función lógica viene expresada como tabla de verdad, se puede elegir la forma canónica para expresar la función. El criterio más lógico es elegir aquella forma que contenga inicialmente el menor número de términos. Para ello basta con contar el número de interpretaciones que satisfacen la fórmula lógica (filas de la tabla de verdad con resultado ‘1’). Cuando el número de interpretaciones que satisfacen la fórmula lógica es menor que el número de interpretaciones que no la satisfacen, se elige la forma canónica DNF. En caso contrario la CNF.

Nota.- Las tablas de Karnaugh se pueden realizar fácilmente a mano con funciones de hasta 6 variables. Para funciones de mayor cantidad de variables es más eficiente el uso de software especializado.

Una vez construida la tabla de Karnaugh se procede a la reducción del número de términos (si es posible) mediante la agrupación de celdas adyacentes en la tabla con valor ‘1’25.

Las dos secciones siguientes describen el algoritmo de simplificación en detalle para las formas canónicas DNF y CNF.

3.3.1 Simplificación de una función lógica expresada en DNF

Dada la tabla de Karnaugh correspondiente a una función lógica expresada en DNF, el procedimiento para su simplificación se describe a continuación.

En primer lugar, se agrupan las celdas con valor ‘1’ de la tabla teniendo en cuenta las siguientes reglas:

  1. Un grupo está formado por un número variable de celdas con valor ‘1’.
  2. El número de celdas con valor ‘1’ dentro de un grupo debe ser potencia de dos: 1, 2, 4, 8, 16.
  3. A efectos de la formación de grupos se debe considerar la tabla como toroidal, pues los extremos de la tabla son adyacentes: el extremo derecho es adyacente al izquierdo, y el inferior al superior. Se puede apreciar mejor en la Fig. 3.226.
  4. Todas las celdas con valor ‘1’ deben pertenecer al menos a un grupo.
  5. Una celda con valor ‘1’ puede pertenecer a varios grupos distintos.
  6. El número de grupos debe ser mínimo.
  7. Cuanto mayor sea el tamaño del grupo, mayor será la simplificación, tanto en número de términos como en número de literales por cada término.
  8. No es necesario que todos los grupos tengan el mismo tamaño.
  9. Por último, puede darse el caso de que la función contenga alguna interpretación ‘x’ que no sea posible (por ejemplo, por representar parte de un sistema físico con combinaciones de entradas que son físicamente imposibles). A las celdas correspondientes a esas interpretaciones se les asigna un valor ‘x’. Dichas celdas no tienen por qué pertenecer a ningún grupo, pero pueden emplearse para agrandar grupos ya existentes.
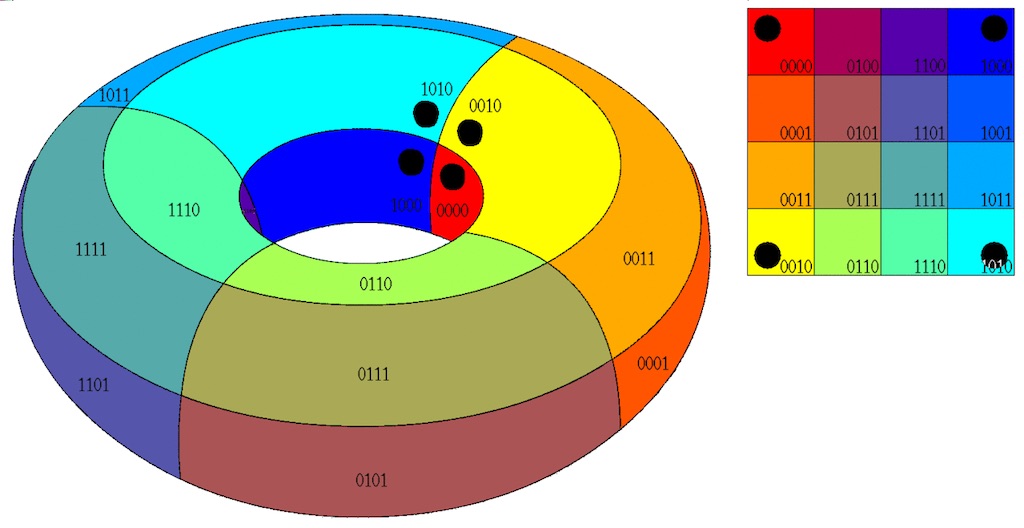
Tabla de Karnaugh dibujado en un toroide y en un plano. Las celdas marcadas con puntos son adyacentes.

Figura 3.2: Tabla de Karnaugh dibujado en un toroide y en un plano. Las celdas marcadas con puntos son adyacentes.

En segundo lugar, cada grupo generará un minitérmino en la función mínima resultante. Ese minterm estará formado por aquellos literales comunes dentro del grupo correspondiente, con signo negativo o positivo si toman el valor ‘0’, o ‘1’ en la codificación Gray. Los literales que aparecen con códigos distintos en el grupo se eliminan.

La función resultante DNF, compuesta por la suma de los minitérminos correspondientes de cada grupo, es mínima.

A modo de ejemplo, se considera la función lógica expresada en la tabla de verdad 3.9:

Tabla 3.9: Ejemplo de tabla de verdad
a b c y
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1

Al tener 3 variables tendremos 23 = 8 celdas. Para construir la codificación Gray inicial, las variables se pueden agrupar como se quieran. En este caso representaremos a y b juntas (columnas) frente a c (filas). La tabla de Karnaugh, con dos formas de representar las cabeceras de filas y columnas, aparece en la Fig. 3.3.

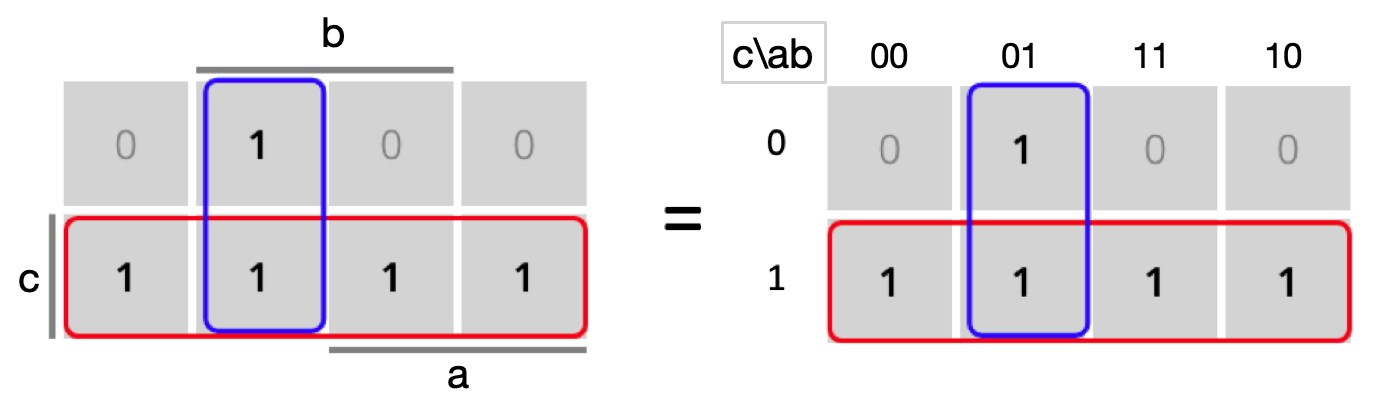
Tabla de Karnaugh DNF

Figura 3.3: Tabla de Karnaugh DNF

En la representación de la izquierda, las cabeceras de las filas y columnas representan con una raya gris los literales positivos (variables con valor ‘1’). Consecuentemente, la ausencia de raya indica los literales negativos (variables con valor ‘0’). En la representación de la derecha aparecen explícitamente los valores de las entradas. En este libro usaremos la notación de la izquierda para las tablas de Karnaugh por su sencillez.

Una vez tenemos la tabla de Karnaugh agrupamos los unos. Como hay 5 celdas con valor ‘1’ no se puede agrupar a todos en un mismo grupo porque no es una potencia de dos. Pero vemos que sí se puede hacer un grupo de 4 unos: el rojo. El ‘1’ que queda suelto podría formar un grupo el sólo, pero si se junta con la celda de valor ‘1’ de la fila inferior se obtiene un grupo más grande: el azul.

El término asociado al grupo rojo sería \(y = c\), ya que dicho literal es el único común a todo el grupo (observe que a y b aparecen con distinto signo -toman valores tanto ‘1’ como ‘0’). El término asociado al grupo azul sería \(y = \overline{a}·b\), porque en este grupo a vale siempre ‘0’ y b siempre ‘1’ mientras que aparecen literales positivos y negativos de la variable c. En consecuencia, la función simplificada sería:

\[y=c+\overline{a}·b\]

3.3.2 Simplificación de una función lógica expresada en CNF

La simplificación de una función en forma canónica CNF es dual con respecto a la metodología vista en la sección anterior para una forma canónica DNF.

Según lo expuesto en la sección 3.2.2, cada fila de ceros de la tabla de verdad produce un maxitérmino de la forma CNF con los signos de los literales opuestos a los valores de las celdas de la tabla. La tabla de Karnaugh, a partir de los maxitérminos, se obtiene de la misma forma que para los minitérminos. La agrupación de las celdas de dicha tabla con valor ‘1’ conduce a los maxitérminos simplificados de la forma canónica CNF original. Se deja al alumno que emplee esta metodología para obtener la simplificación del ejemplo anterior (tabla de la Fig. 3.3).

Como metodología alternativa, y partiendo de la tabla de Karnaugh obtenida para los minitérminos en la sección anterior (Fig. 3.3), se puede obtener la fórmula CNF mínima agrupando las celdas con valor ‘0’ de dicha tabla de acuerdo con las reglas generales ya expuestas (ver Fig. 3.4, agrupaciones violeta y verde). Si se razona de esta forma, cada grupo de celdas con valor ‘0’ produce un maxitérmino siempre y cuando se consideren sus literales con signo opuesto a los que les corresponden en la codificación Gray de la tabla de Karnaugh original.

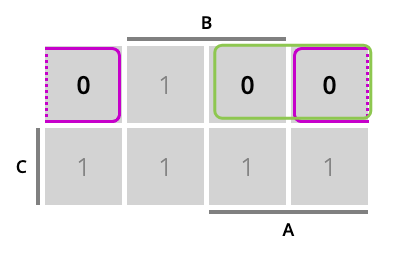
Tabla de Karnaugh CNF

Figura 3.4: Tabla de Karnaugh CNF

En el ejemplo, el término asociado al grupo violeta es \(y=(c+b)\), pues c siempre aparece negado (y consideramos el literal con el signo cambiado), b también aparece siempre negado (así que aparece con signo también positivo) y a cambia de signo (con lo que se elimina). Razonando de la misma manera puede verse que el término asociado al grupo verde es \(y=(c+\overline{a})\). La función mínima CNF es, por tanto:

\[y=(c+b)·(c+\overline{a})\]

Ejercicio.- Demuestre que las expresiones canónicas mínimas CNF y DNF obtenidas corresponden a la misma función (tienen exactamente las mismas interpretaciones que las satisfacen).

Ejercicio.- Simplifique la función ‘y’ dada por la siguiente tabla de verdad.

Tabla 3.10: Tabla de verdad del ejercicio
a b c d y
0 0 0 0 0
0 0 0 1 1
0 0 1 0 0
0 0 1 1 1
0 1 0 0 0
0 1 0 1 1
0 1 1 0 1
0 1 1 1 1
1 0 0 0 0
1 0 0 1 1
1 0 1 0 0
1 0 1 1 1
1 1 0 0 0
1 1 0 1 1
1 1 1 0 0
1 1 1 1 1

Solucion

La solución al ejercicio es:

\[y = d + (\overline{a}·b·c)\]

  1. Debe su nombre a Maurice Karnaugh, un físico y matemático de los laboratorios Bell, quien lo inventó en 1953↩︎

  2. Por la naturaleza dual las dos formas canónicas, también es posible razonar con las celdas de valor ‘0’ de la tabla (las que no dan lugar a minitérminos) con consideraciones adicionales. La sección 3.3.2 muestra un ejemplo.↩︎

  3. Por Jochen Burghardt - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=28286441↩︎