6.7 Ejercicios resueltos

6.7.1 Control de entrada y salida

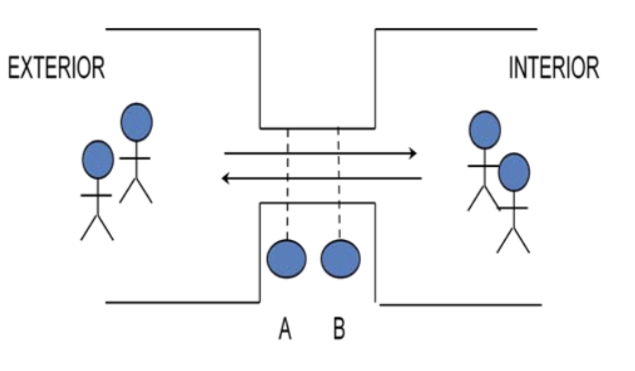
Se desea diseñar el control de entradas y salidas de un recinto mediante dos sensores ópticos A y B situados en un estrechamiento que sólo puede estar ocupado por una única persona (bien para entrar en el recinto, bien para salir del mismo). Se considera en el diseño la máquina de estados que devuelve un ‘1’ si la persona entra en el recinto y un ‘0’ si sale del mismo. Asimismo se consideran dos posibles configuraciones de los sensores A y B:

  1. NO es posible situarse entre A y B sin ser detectado
  2. SI es posible situarse entre A y B sin ser detectado.

Nota: NO considere comportamientos anómalos de las personas.

Se pide:

  1. Considere los estados, NO_PERSONA, ENTRANDO y SALIENDO en las dos configuraciones. Indique sin son adecuados en cada caso y justifique la respuesta brevemente (ponga un contraejemplo en caso negativo).
  2. Tabla de transición de estados y diagrama de estados para la configuración 1. En el caso del diagrama, dibuje solo los arcos dirigidos que producen un cambio de estado.
  3. Ecuaciones de activación, retención y salida del modelo del apartado anterior.
  4. Considere un diseño para la configuración 2 con los 5 estados siguientes: NO_PERSONA, ENTRANDO_10, ENTRANDO_00, SALIENDO_01, SALIENDO_00 —el primer dígito corresponde a A y el segundo a B—. Indique si esta configuración es adecuada razonando sobre el diagrama de estados
  5. Proponga un diseño con el mínimo número de estados posible para la configuración 2 y dibuje el diagrama de estados.

Solucion

APARTADO 1 Considere los estados, NO_PERSONA, ENTRANDO y SALIENDO en las dos configuraciones. Indique sin son adecuados en cada caso y justifique la respuesta brevemente (ponga un contraejemplo en caso negativo).

Configuración 1: Los estados son adecuados.

Configuración 2: Los estados NO son adecuados. Como ejemplo, el estado SALIENDO no tiene suficiente expresividad ya que pueden estar los dos sensores a nivel bajo como consecuencia de que un individuo está en el pasillo tras atravesar B—y no ser visible para A— o bien el individuo acaba de salir al exterior tras cruzar A.

APARTADO 2 Tabla de transición de estados y diagrama de estados para la configuración 1. En el caso del diagrama, dibuje solo los arcos dirigidos que producen un cambio de estado.

Qt 00 01 10 11 Salida
NO NO S E X 1
E NO E E E 1
S NO S S S 0

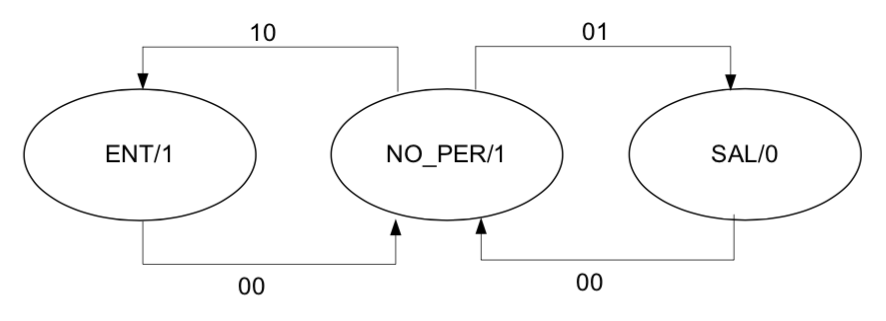
APARTADO 3 Ecuaciones de activación, retención y salida del modelo del apartado anterior.

\[N_{t+1} = (E_t + S_t)· \overline{A}· \overline{B} + N_t · (\overline{S_{t+1} + E_{t+1}}) \] \[ E_{t+1} = N_t ⋅ A + E_t· \overline{N_{t+1}} \] \[ S_{t+1} = N_t · B + S_t · \overline{N_{t+1}} \]

APARTADO 4 Considere un diseño para la configuración 2 con los 5 estados siguientes: NO_PERSONA, ENTRANDO_10, ENTRANDO_00, SALIENDO_01, SALIENDO_00 —el primer dígito corresponde a A y el segundo a B—. Indique si esta configuración es adecuada razonando sobre el diagrama de estados.

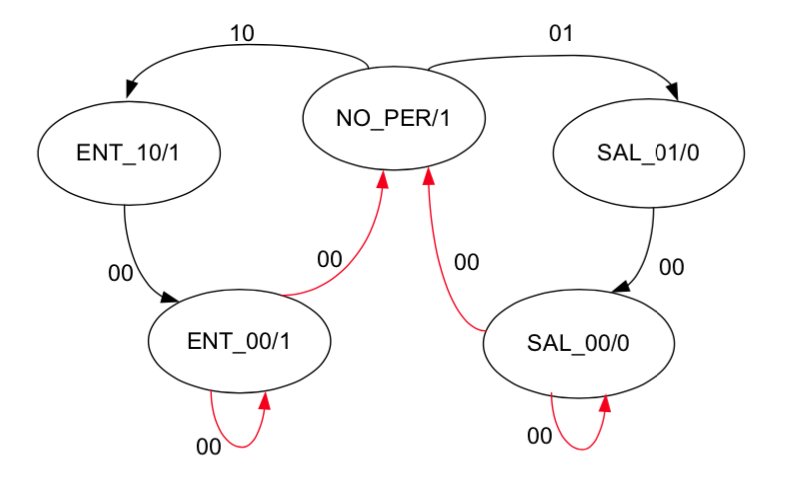
APARTADO 5 Proponga un diseño con el mínimo número de estados posible para la configuración 2 y dibuje el diagrama de estados.

Se necesita ampliar el modelo con los estados de SALIENDO_10 y ENTRANDO_01. Se pueden entonces simplificar los estados ENTRANDO_10 y ENTRANDO_00, así como SALIENDO_01 y SALIENDO_00 con lo que la máquina tendría finalmente 5 estados: NO_PERSONA, ENTRANDO_10_00, SALIENDO_01_00, ENTRANDO_01 y SALIENDO_10.

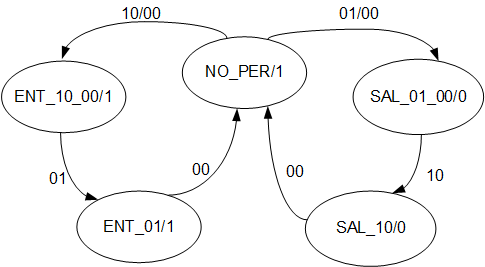
Nota.- Se puede observar que esta máquina de estado es equivalente a la vista en el ejemplo de la sección 6.6.4.2.

6.7.2 Reconocedor de cadenas (AB)

Se desea diseñar una máquina de estados síncrona para modelar un reconocedor de cadenas de un lenguaje \(\Sigma\) que tiene un alfabeto de dos letras A y B. La cadena se construye de dos en dos letras mediante las entradas \(x1 \in \Sigma\), \(x2 \in \Sigma\) y en la forma <x1><x2>. El sistema indica mediante una salida ‘y’ a 1 que la cadena formada contiene la secuencia de 3 letras consecutivas “ABA”.

A modo de ejemplo, se presenta una traza del funcionamiento de dicho sistema:

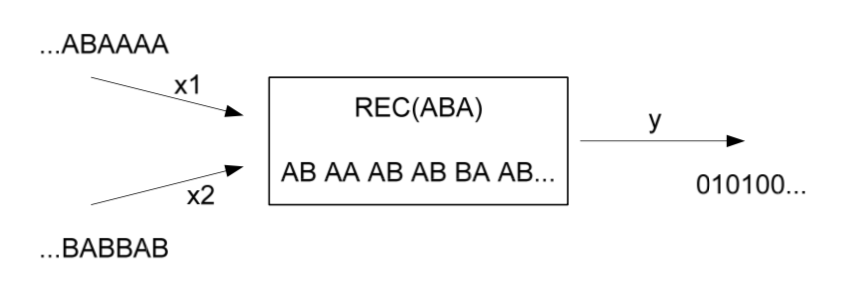
ACLARACIONES: Hay un nuevo valor en la salida para cada pareja de letras <x1><x2> que se añaden a la cadena. En el ejemplo de la figura, el primer ‘1’ de la salida se debe a que, tras la entrada de la segunda pareja <x1:=A><x2:=A> al modelo, la cadena resultante “ABAA” contiene la secuencia buscada (las tres primeras letras). Un razonamiento análogo puede hacerse para el segundo ‘1’ de la salida.

Importante: No se pueden emplear letras de secuencias reconocidas como parte de otras secuencias reconocidas. Ejemplo: la cadena “AB AB AB” produce como salida la secuencia y:= “010” y no y:=“011”.

Considere los estados siguientes: X_N (ninguna letra de la secuencia buscada reconocida), X_A (primera letra de la secuencia buscada reconocida), X_AB (dos primeras letras de la secuencia buscada reconocida) y X_ABA (secuencia buscada reconocida).

Se pide:

  1. Demuestre que los estados elegidos corresponden a una máquina de Mealy.
  2. Tabla de transición de estados.
  3. Ecuación de retención del estado X_N (función lógica simplificada y diagrama de escalera).
  4. Ecuación de activación del estado X_A (función lógica simplificada y diagrama de escalera).
  5. ¿Se puede simplificar alguna pareja de estados? Justifique la respuesta. En caso afirmativo, dibuje el diagrama de estados de la máquina simplificada (incluya solo los arcos correspondientes a la activación de nuevos estados).
  6. Indique un nuevo conjunto de estados para obtener una máquina de Moore. Justifique la respuesta.

Solucion

Apartado 1 Demuestre que los estados elegidos corresponden a una máquina de Mealy

Basta con encontrar un ejemplo de salidas distintas desde un mismo estado: desde X_A ante entrada AA la salida es 0 y ante entrada BA la salida es 1 (cadena ABA).

Apartado 2 Tabla de transición de estados

Qt/Entradas AA AB BA BB
X_N X_A , 0 X_AB, 0 X_A, 0 X_N, 0
X_A X_A, 0 X_AB,0 X_ABA, 1 (ó X_N,1) X_N, 0
X_AB X_A, 1 (no X_ABA) X_N, 1 X_A, 0 X_N, 0
X_ABA X_A, 0 X_AB, 0 X_A, 0 X_N, 0

Apartado 3 Ecuación de retención del estado X_N (función lógica simplificada y diagrama de escalera).

\[X\_N_{k+1} = X\_N_k · (\overline{X\_A}·\overline{X\_AB})\]

También sería válido expresarlo en función de las entradas:

\[X\_N_{k+1} = X\_N_k · (BB)\]

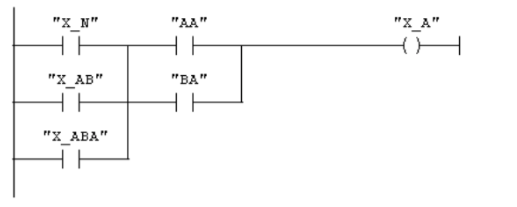
Apartado 4 Ecuación de activación del estado X_A (función lógica simplificada y diagrama de escalera).

Tendríamos:

\[X\_A_{k+1} = X\_N_k · (AA + BA) + X\_AB_K · (AA+BA) + X\_ABA_K · (AA+BA)\]

el estado X_A se activa desde cualquier otro estado, siempre que la segunda letra de la entrada sea una A.

Apartado 5 ¿Se puede simplificar alguna pareja de estados? Justifique la respuesta. En caso afirmativo, dibuje el diagrama de estados de la máquina simplificada (incluya solo los arcos correspondientes a la activación de nuevos estados).

Se pueden simplificar los estados X_ABA y X_N. La máquina evoluciona de la misma manera desde ambos estados y la salida es la misma (las filas de la tabla de estados son iguales).

Qt/Entradas AA AB BA BB
X_N X_A , 0 X_AB, 0 X_A, 0 X_N, 0
X_A X_A, 0 X_AB X_N, 1 X_N, 0
X_AB X_A, 1 X_N, 1 X_A, 0 X_N, 0

El diagrama de estados se dibuja sin mayor dificultad a partir de la tabla de estados.

Apartado 6 Indique un nuevo conjunto de estados para obtener una máquina de Moore. Justifique la respuesta.

Existen diferentes soluciones de diseño. Una posibilidad es definir estados que garanticen que la salida sea 1 tras la llegada de parejas de entradas. Por ejemplo:

  • Estado X_1: Cadena reconocida ABA tras llegada de AB
  • Estado X_2: Cadena reconocida ABA tras llegada de AA
  • Estado X_3: Cadena reconocida ABA tras llegada de BA

Estos tres estados capturan todas las posibles formas de que se produzca una secuencia ABA: X_1 se activa cuando teniendo un AB en el buffer llega AB. X_2 se activa cuando teniendo un AB en el buffer llega AA. Finalmente X_3 se activa cuando teniendo una A en el buffer, llega BA.

Complementando los tres estados anteriores con X_A, X_AB y X_N, con la misma semántica que en el diseño inicial, se garantiza suficiente expresividad para formar la máquina de Moore.

Nota: Es posible que se puedan simplificar estados en un análisis posterior.

6.7.3 Control de una escalera mecánica

Se desea realizar el sistema de control de una escalera mecánica bidireccional. Para ello se dispone de dos sensores de presión, P1 y P2, como se muestra en la figura adjunta. Cuando se activa un sensor, la escalera empezará a andar en dirección al otro sensor y no parará hasta que se active el otro sensor. La máquina deberá mostrar el comportamiento de la dirección de los motores (D=0 bajando, D=1 subiendo), así como su estado (E=1 encendido, E=0 apagado).

Las posibles secuencias que hay que describir son las siguientes:

  • Si una persona se coloca sobre el sensor P1, la escalera debe empezar a bajar hasta que dicha persona se coloque sobre el sensor P2 (y viceversa)
  • Cuando no se active ninguno de los sensores la escalera debe permanecer parada.

No se ha considerado la situación de que se coloquen de forma simultánea dos personas sobre P1 y P2 porque no ha sido contemplada en las especificaciones de diseño.

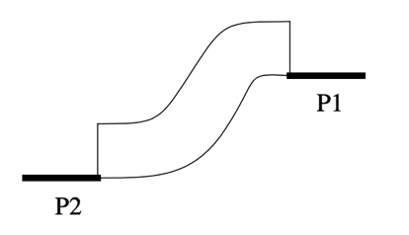
Ejercicio de control de escalera mecánica

Figura 6.35: Ejercicio de control de escalera mecánica

Se pide:

  1. Identificar entradas y salidas del sistema.
  2. Indicar si se trata de un sistema combinacional o secuencial, y demostrarlo.
  3. Diseñar el sistema. Para ello:
    1. Dibuje el diagrama de máquina de estados de Mealy que implemente el sistema descrito.
    2. Escriba la tabla de transición de estados. Simplifique los estados en caso de que sea posible.
    3. Obtenga razonadamente las ecuaciones de activación y retención de los estados y de las salidas.
    4. Implemente el sistema mediante un esquema de contactos.
  4. Indique si se podría implementar una máquina de Moore y, en caso afirmativo, dibuje el diagrama.

Solucion

Apartado 1

Las entradas serían los pulsadores P1 y P2 y las salidas las señalas E y D.

Apartado 2

Es un sistema secuencial. Se puede demostrar de muchas formas. Por ejemplo, cuando no se active ni P1 ni P2, la escalera a veces subirá y a veces bajará, dependiendo del estado en el que esté.

Apartado 3

  1. La máquina de estados se muestra a continuación. Se suponen los estados Reposo, Subiendo y Bajando. La nomenclatura utilizada en “P1P2 / ED”.
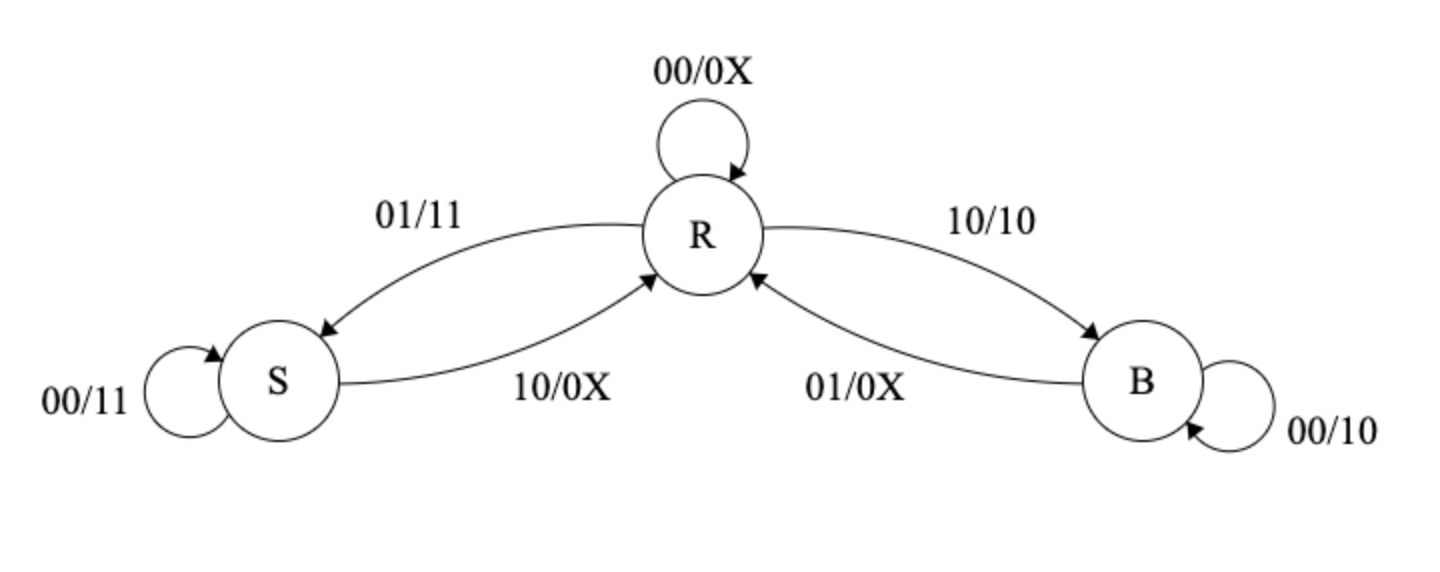
Ejercicio de control de escalera mecánica: máquina de estados de Mealy

Figura 6.36: Ejercicio de control de escalera mecánica: máquina de estados de Mealy

La “X” en las salidas indica que se puede poner tanto ‘0’ como ‘1’.

  1. La tabla de transición de estados será:
Qt/Entradas(P1·P2) 00 01 11 10
R R/0X S/11 X B/10
B B/10 R/0X X B/10
S S/11 S/11 X R/0X

No se pueden simplificar estados.

  1. De aquí se pueden obtener las ecuaciones de activación y retención de los estados:

\[ R = B·P_2 + S·P_1 + R·\overline{B}·\overline{S} \] \[ B = R·P_1 + B·\overline{R}\] \[ S = R·P_2 + S·\overline{R}\]

y de las salidas:

\[ D = R·P_2 + S \] \[ E = R·(P_1 + P_2) + B·\overline{P_2} + S·\overline{P_1} \]

  1. Finalmente, el esquema de contactos sería:
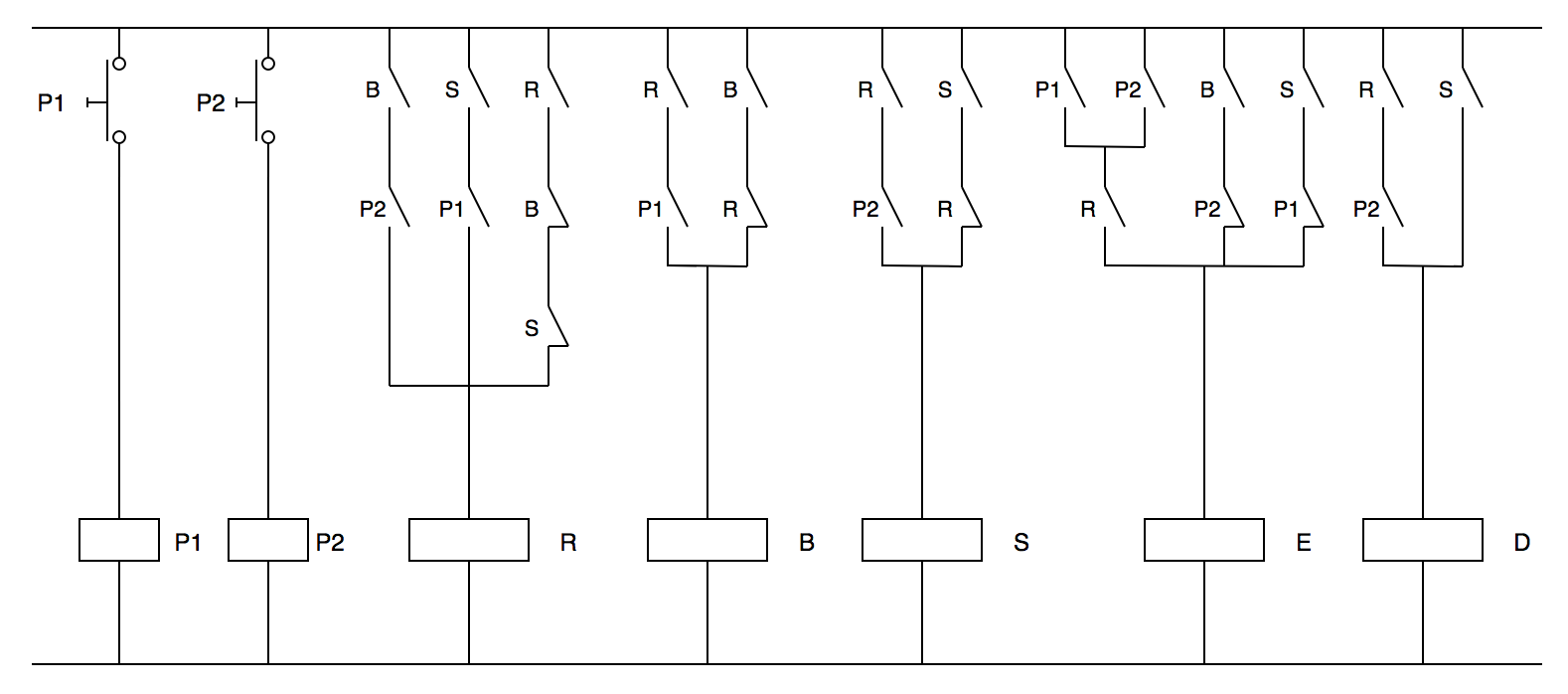
Ejercicio de control de escalera mecánica: diagrama de contactos

Figura 6.37: Ejercicio de control de escalera mecánica: diagrama de contactos

Apartado 4

Como todos los sistemas secuenciales, también se puede representar como una máquina de Moore. A continuación se muestra una posible implementación.

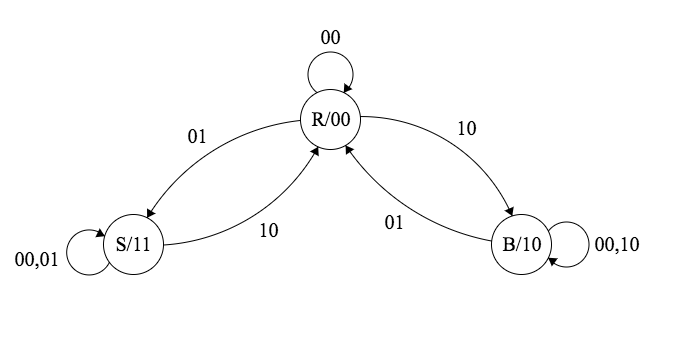
Ejercicio de control de escalera mecánica: máquina de estados de Moore

Figura 6.38: Ejercicio de control de escalera mecánica: máquina de estados de Moore