5.1 Ejercicios resueltos
5.1.1 Control de una luz
Un pasillo cuenta con una luz (L) y dos interruptores (A y B), cada uno de ellos con dos posiciones (derecha e izquierda). Para que la luz se encienda los interruptores deben estar en posiciones distintas. Si los dos están a la derecha, la luz estará apagada. Cuando se modifique uno, la luz se encenderá. Y cuando, a continuación, se modifique el otro, se apagará.
Se pide la función booleana que expresa el comportamiento de la luz en función de los dos interruptores.
Lo primero que debemos hacer es la tabla de verdad mostrada en la Tabla 5.1.
| A | B | L |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
De la tabla de verdad obtendremos la salida que será:
\[L=\overline{A}·B + A·\overline{B} = A \oplus B \]
En este ejemplo, dado su sencillez, la expresión lógica obtenida es óptima en cuanto al número de términos.
5.1.2 Control de otra luz
Se quiere diseñar un sistema de tres interruptores (B1, B2 y B3) y una bombilla (L), de manera que se encienda L cuando haya al menos dos interruptores activados.
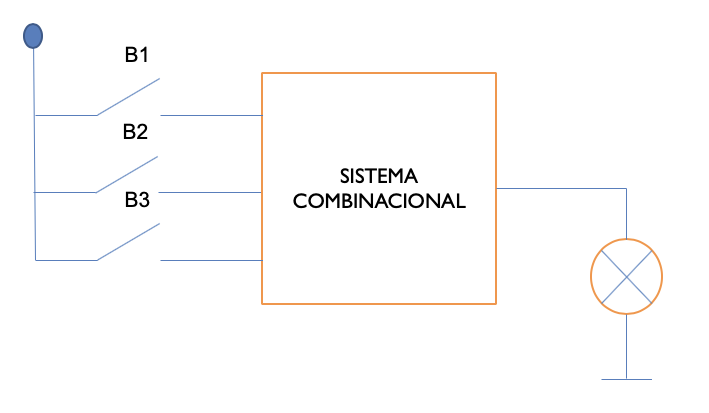
Figura 5.1: Control de luces mediante tres interruptores
La tabla de verdad sería la mostrada en la Tabla 5.2.
| B1 | B2 | B3 | L |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
La tabla de Karnaugh correspondiente a la forma canónica DNF, agrupando los términos por colores, es la siguiente:
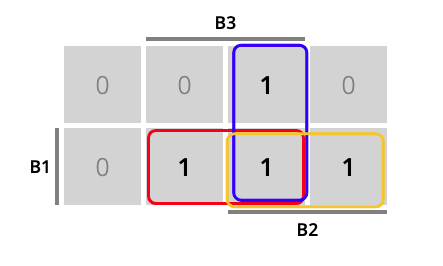
Figura 5.2: Control de luces mediante tres interruptores
Del grupo rojo obtenemos el término \(B_1·B_3\), del naranja \(B_1·B_2\) y del azul \(B_2·B_3\). En total:
\[L=B_1·B_3 + B_1·B_2 + B_2·B_3\]
5.1.3 Ejercicio de depósitos
En una nave se han instalado tres depósitos de aceite de oliva (d1, d2 y d3). Cada uno de ellos tiene instalado una boya en la parte superior para indicar que está completamente lleno. Para señalizar de forma simple el estado del conjunto de los depósitos, se ha colocado un panel a la entrada de la nave que tiene tres pilotos de colores diferentes: Rojo (R), Naranja (N) y Verde (V).
La lógica de los pilotos es la siguiente:
- El piloto V se activa cuando no hay ningún depósito lleno.
- El piloto N se activa cuando hay un único depósito lleno.
- El piloto R se activa cuando el número de depósitos llenos es mayor que 1.
Se pide obtener las ecuaciones lógicas simplificadas del control de los tres pilotos.
5.1.4 Ejercicio de simplificación
Dada la siguiente función:
\[ S = a·b + \overline{a}·\overline{c} + a·\overline{b}·\overline{c} + \overline{a}·b \]
Obtenga su expresión más simplificada.
Solucion
En primer lugar podemos simplificar directamente algunos términos. En concreto, el primer y el último minterm darían ‘b’:
\[ S = b + \overline{a}·\overline{c} + a·\overline{b}·\overline{c} \]
A partir de aquí podemos continuar simplificando, expandir los términos para hacer la tabla de verdad o hacer la tabla de verdad directamente.
Si la hacemos directamente debemos dar valores a las variables para ir rellenándola. Vemos que si b vale ‘1’ entonces S vale ‘1’ directamente. Y si b vale ‘0’, S valdría \(\overline{c}\).
| a | b | c | S |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Mediante Karnaugh obtendríamos:
\[ S = b + \overline{c} \]