6.3 Tabla de transición de estados
Las máquinas de estados de sistemas secuenciales también se pueden representar mediante una tabla en la que, a diferencia de la tabla de verdad de los sistemas combinacionales, se muestran no solo las funciones de salida sino también las funciones de transición de estado (el cuarto elemento de la 5-tupla, \(\delta\)).
En las máquinas de Moore en las que la salida depende de un único estado, algo frecuente en los sistemas de control automático, las filas de la tabla de transición representan estados y las columnas entradas y salidas (un ejemplo aparece en la Tabla 6.3).
| m \ x1x2 | 00 | 01 | 11 | 10 | Salida |
|---|---|---|---|---|---|
| m00 | m00 | m01 | m10 | m01 | 0 |
| m01 | m00 | m01 | m10 | m01 | 1 |
| m10 | m01 | m10 | m11 | m10 | 0 |
| m11 | m01 | m10 | m11 | m10 | 1 |
En una máquina de Mealy se representan estados (filas) frente a entradas (columnas). Los valores de las salidas, puesto que dependen del estado, aparecen en cada celda, tal y como se muestra a modo de ejemplo en la Tabla 6.4.
| m \ x1x2 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| m0 | m0,0 | m0,1 | m1,0 | m0,1 |
| m1 | m0,1 | m1,0 | m1,1 | m1,0 |
Cada fila de la tabla representa el estado activo en un instante determinado k. En cada celda puede leerse el conjunto de estados que se activarían para la combinación de entradas de la columna correspondiente de la celda en el instante k+1. Los valores de las salidas en una celda se corresponden con la combinación de estado/entradas de la fila/columna. Observe que no dependen de los estados futuros en la misma celda.
Un posible inconveniente que puede darse en la máquina de Mealy es el siguiente. Partiendo de la Tabla 6.4, supongamos que estamos en el estado m0 y las entradas son “11”. Según la tabla se debería pasar al estado m1 y la salida debería pasar a ser ‘0’. Sin embargo, podría ocurrir que al pasar al estado m1, las entradas continuaran siendo “11”, y por tanto la salida debería pasar a ser ‘1’. Si la transición es muy rápida, podría incluso ocurrir que la salida pasara a ser ‘1’ sin pasar por ‘0’. Esta es una de las razones por las que se emplean diseños basados en máquinas de Moore en automatismos.
6.3.1 Ecuaciones de activación y retención a partir de la tabla de transición de estados
A partir de la tabla de transición podemos obtener las ecuaciones simplificadas de activación y retención y salida para cada uno de los estados construyendo las correspondientes tablas de Karnaugh, pues dichas ecuaciones representan subsistemas combinacionales. Por ejemplo, consideremos la tabla de transición de estados de la máquina de Moore dada por la Tabla 6.3. Para calcular las ecuación de activación de m10 se consideran los valores de las filas de los estados desde los que se llega a m10, es decir m00 (con entradas “11”), m01 (con entradas “11”) y m11 (con entradas “01” y “10”).
La tabla de Karnaugh para la activación del estado m10 desde m11 puede verse en la Fig. 6.8.
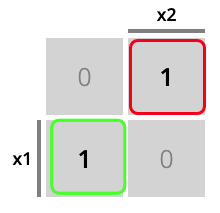
Figura 6.8: Tabla de Karnaugh
En este caso no se puede simplificar y obtendríamos la ecuación:
\[m_{10}=m_{11} · (x_1\overline{x_2} + \overline{x_1}x_2)\]
Simplificando vía Karnaugh la activación del estado m10 a partir del resto de estados (m00 y m01) se obtiene la ecuación completa de activación del estado m10:
\[m_{10} = m_{00} · x_1x_2 + m_{01} · x_1x_2 + m_{11} · (x_1\overline{x_2} + \overline{x_1}x_2)\] La ecuación de retención del estado m10 se obtiene de forma análoga. Se hace un diagrama de Karnaugh a partir de la fila del estado m10, con unos en las entradas en las que se mantiene el estado m10, y ceros en las que evoluciona a otro estado. Casualmente, el diagrama es el mismo que el de la Fig. 6.8. La ecuación de retención para m10 quedaría:
\[m_{10} = m_{10} · (x_1\overline{x_2} + \overline{x_1}x_2)\] Y la ecuación completa de m10 sería la suma de la de activación y retención:
\[m_{10} = m_{00} · x_1x_2 + m_{01} · x_1x_2 + m_{11} · (x_1\overline{x_2} + \overline{x_1}x_2)+ m_{10} · (x_1\overline{x_2} + \overline{x_1}x_2)\]