6.6 Ejemplos

6.6.1 Sumador binario

Vamos a implementar un sumador binario de dos entradas, x₁ y x₂, y una salida y. El esquema se puede ver en la Fig. 6.16.

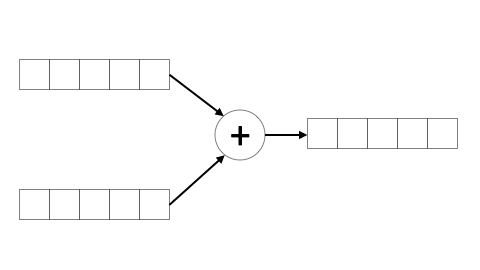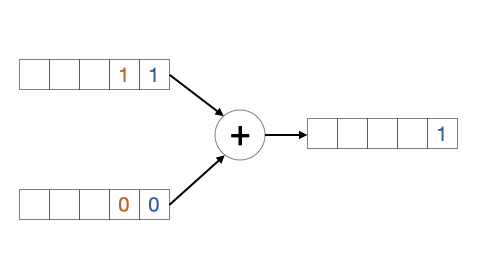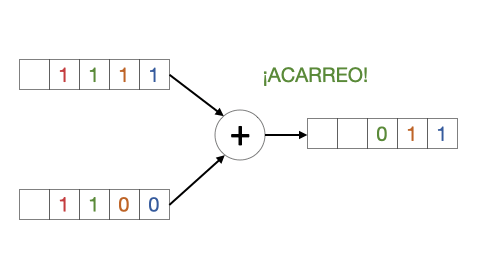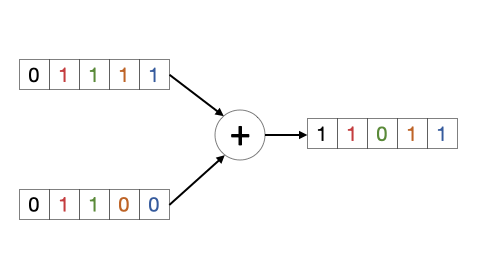
Figura 6.16: Sumador binario

La suma binaria responde a la Tabla 6.21.

Tabla 6.21: Tabla de verdad del ejercicio del sumador binario

x1	x2	y	Acarreo
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Claramente es un sistema secuencial porque la suma de dos bits depende de la suma anterior, es decir, del acarreo. Por ejemplo, si sumamos en binario “11” y “11”, en la primera suma de ‘1’ y ‘1’ el resultado será ‘0’ y el acarreo ‘1’. Pero en la siguiente suma de ‘1’ y ‘1’, hay que añadir el acarreo anterior, y por tanto el resultado será ‘1’ y el acarreo ‘1’.

Máquina de estados

Por lo visto anteriormente parece lógico elegir dos estados: m₀ representa el estado en el que no hay acarreo y m₁ el estado en el que sí hay. Para estos dos estados, el diagrama de estados aparece dibujado en la Fig. 6.7. Repetimos el diagrama aquí (Fig. 6.17) para facilitar la lectura. La notación en los arcos corresponde al patrón de variables \(x_1,x_2/y\).

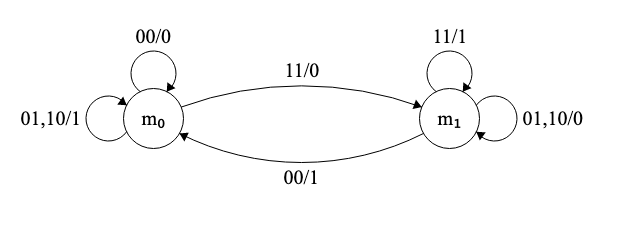
Figura 6.17: Diagrama de estados para sumador binario

La máquina propuesta se corresponde con una máquina de Mealy, pues la salida depende del estado y de las entradas. Por ejemplo, en m₀, si las entradas valen “00” ó “11” la salida vale ‘0’, y si las entradas son “01” ó “10” la salida vale ‘1’.

Funciones de transición y de salida

Para la máquina de Mealy las funciones de transición \(\delta\) y de salida \(\beta\) serían las ecuaciones (6.1) y (6.2) respectivamente:

\[\begin{equation} \begin{aligned} \delta(m_0,11) &:= m_1 \\ \delta(m_1,00) &:= m_0 \\ \delta(m_0,00/01/10) &:= m_0 \\ \delta(m_1,10/01/11) &:= m_1 \end{aligned} \tag{6.1} \end{equation}\]

\[\begin{equation} \begin{aligned} \beta(m_0,00/11) &:= 0 \\ \beta(m_0,01/10) &:= 1 \\ \beta(m_1,00/11) &:= 1 \\ \beta(m_1,01/10) &:= 0 \end{aligned} \tag{6.2} \end{equation}\]

Tabla de verdad

La tabla de verdad para este sistema sería la mostrada en la Tabla 6.22.

Tabla 6.22: Tabla de verdad del ejercicio del sumador binario con estados

x1	x2	mk	mk+1	y
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Y las ecuaciones:

\[m_{k+1}=\delta=x_1·x_2 + x_1·m_k + x_2·m_k \tag{6.3}\]

\[y=\beta=x_1·\overline{x_2}·\overline{m_k} + \overline{x_1}·x_2·\overline{m_k} + \overline{x_1}·\overline{x_2}·m_k + x_1·x_2·m_k \tag{6.4}\]

A partir de la función de transición mostrada en la Eq. (6.3) se deduce que el estado de acarreo se activa (hay acarreo real) cuando al menos dos de las variables que intervienen toman el valor “1”. En otras palabras, habrá acarreo cuando bien los dos sumandos valen “1”, bien un sumando vale “1” y hay un acarreo anterior.

Ejercicio.- Se deja al lector hacer una interpretación similar para la Eq. (6.4) de las salidas.

 

Tanteo con máquina de Moore

Se ha podido comprobar que el diseño anterior no se corresponde con una máquina de Moore. Por tanto se propone como ejercicio diseñar una máquina de Moore partiendo de los dos estados m₀ y m₁ vistos anteriormente. Para ello, al ser una máquina de Moore, deberemos asignar una salida a cada estado. ¿Qué salida asignamos a m₀? ¿‘0’? ¿‘1’? Vemos que ninguna de las opciones es correcta.

Esto es debido a que dos estados no son suficiente para codificar la información necesaria en una máquina de Moore para el sumador binario.

Pasaremos entonces a intentarlo con cuatro estados añadiendo un estado más con semántica de salida para cada uno de los estados anteriores:

• m₀₀: estado de no acarreo con salida y=0
• m₀₁: estado de no acarreo con salida y=1
• m₁₀: estado de acarreo con salida y=0
• m₁₁: estado de acarreo con salida y=1

Para estos estados, la nueva máquina (de tipo Moore) se corresponde con la Figura 6.6 y se repite aquí (Figura 6.18) para facilitar la lectura. En este caso los arcos muestran solamente valores de las entradas \(x_1x_2\); los valores de la salida aparecen dentro de los estados.

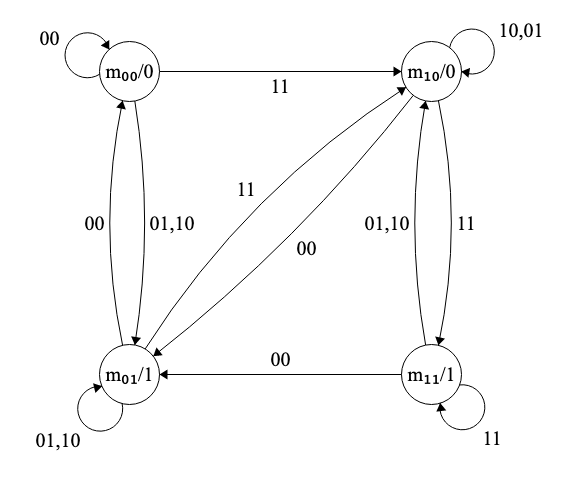
Figura 6.18: Diagrama de estados para sumador binario (versión Moore)

Para la máquina de Moore las funciones de transición \(\delta\) y de salida \(\lambda\) serían las ecuaciones (6.5) y (6.6) respectivamente:

\[\begin{equation} \begin{aligned} \delta(m_{00}/m_{01},00) &:= m_{00} \\ \delta(m_{10}/m_{11},00) &:= m_{01} \\ \delta(m_{00}/m_{01},01/10) &:= m_{01} \\ \delta(m_{00}/m_{01},11) &:= m_{10} \\ \delta(m_{10}/m_{11},11) &:= m_{11} \\ \delta(m_{10}/m_{11},01/10) &:= m_{10} \end{aligned} \tag{6.5} \end{equation}\]

\[\begin{equation} \begin{aligned} \lambda(m_{00}/m_{10}) &:= 0 \\ \lambda(m_{01}/m_{11}) &:= 1 \end{aligned} \tag{6.6} \end{equation}\]

Ejercicio.- Indique otra posible conversión de Mealy a Moore (estados con semántica de entradas) para el sumador binario.

 

Tabla de transición de estado

Las tablas de transición de estado para las dos máquinas se corresponden con las Tablas 6.3 y 6.4 vistas en la sección 6.3.

6.6.2 Detector de secuencia binaria

En este ejercicio vamos a implementar un detector de secuencias binarias. En este caso será la secuencia “101”. En la Fig. 6.19 podemos ver un diagrama del reconocedor. Consta de una entrada x y una salida y. Por la entrada x van llegando bits. Cuando se detecta la secuencia “101” la salida vale ‘1’, y cuando no ‘0’. Como aclaración, la secuencia “10101” es una sola secuencia reconocida, no dos.

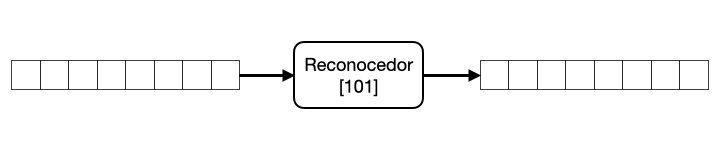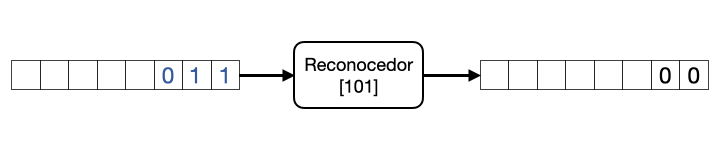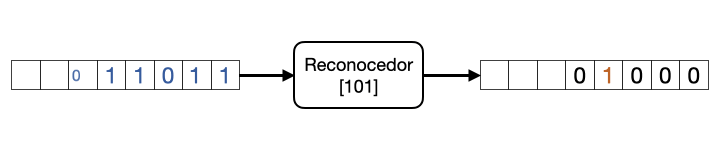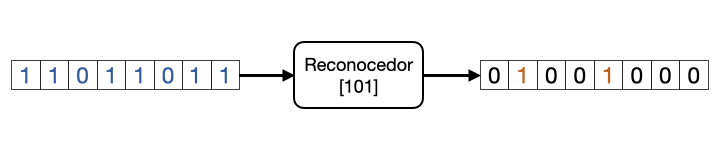
Figura 6.19: Diagrama de sistema recocedor de secuencias binarias

Partimos de un estado inicial, correspondiente al caso de que no se ha reconocido ninguna letra de la secuencia, y elegimos el resto de estados con semántica de cada nueva subcadena reconocida. El último estado corresponde con la secuencia completa “101”. Por tanto, los estados serían:

• m_n: ningún símbolo reconocido
• m₁: subcadena 1 reconocida
• m₁₀: subcadena 10 reconocida
• m₁₀₁: cadena 101 reconocida

El diagrama se puede ver en la Fig. 6.20.

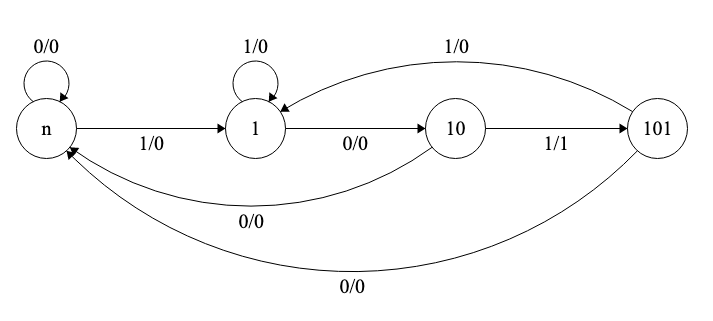
Figura 6.20: Máquina de estados de Mealy del sistema recocedor de secuencias binarias

 

Nota.- Aunque en este libro se suele utilizar una nomenclatura para los estados que empieza por la letra m, de ahora en adelante se suprimirá esta letra en los diagramas para una mayor legibilidad.

Ejercicio.- Justifique que es un sistema secuencial. Indique si se trata de una máquina de Moore o de Mealy.

 

La siguiente fase es realizar la tabla de transición de estados, mostrada en la Tabla 6.23.

Tabla 6.23: Tabla de verdad del ejercicio del sumador binario con máquina de Mealy

m \ x	0	1
mn	mn/0	m1/0
m1	m10/0	m1/0
m10	mn/0	m101/1
m101	mn/0	m1/0

Se puede apreciar que esta tabla es simplificable ya que la primera y la última fila son iguales (los estados m_n y m₁₀₁ son equivalentes). Eliminando el estado m₁₀₁, la tabla de transición y el diagrama de estados se corresponden con la Tabla 6.24 y la Figura 6.21.

Tabla 6.24: Tabla de verdad del ejercicio del sumador binario con máquina de Mealy simplificada

m \ x	0	1
mn	mn/0	m1/0
m1	m10/0	m1/0
m10	mn/0	mn/1

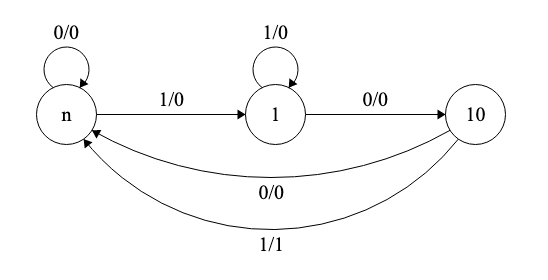
Figura 6.21: Máquina de estados de Mealy simplificada del sistema recocedor de secuencias binarias

Podemos ya desvelar que la máquina anterior era de Mealy. Una máquina de Moore para este sistema puede obtenerse sin más que “desplazar” la salida con valor ‘1’ del arco al estado m₁₀₁ en la Fig. 6.20. Este diseño es mucho más natural ya que el estado que representa la secuencia buscada es el que tiene la salida asociada.

La máquina queda representada en la Tabla 6.25 y la Fig. 6.22.

Tabla 6.25: Tabla de verdad del ejercicio del sumador binario con con máquina de Moore

m \ x	0	1	Salida
mn	mn	m1	0
m1	m10	m1	0
m10	mn	m101	0
mn101	mn	m1	1

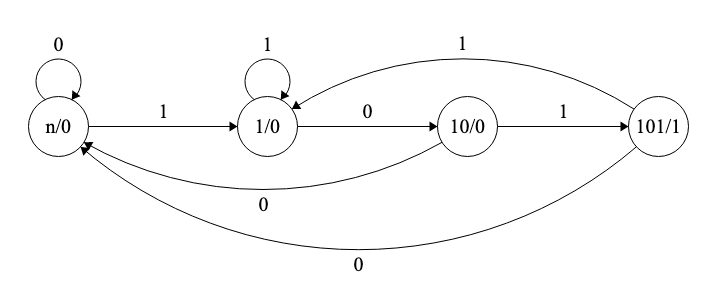
Figura 6.22: Máquina de estados de Moore del sistema recocedor de secuencias binarias

Obsérvese que dado que el estado m₁₀₁ tiene semántica de salida, no es equivalente al estado m_n y la máquina de Moore no puede simplificarse.

Nota.- En general, la máquinas de estado de Mealy tienen menos estados que las de Moore. Sin embargo, tanto por presentar una mayor estabilidad en la salida como por la claridad del diseño, se recomienda el uso de máquinas de Moore (al menos como estructura general) para el control automático.

 

6.6.3 Control de una vagoneta

Se desea implementar el sistema de control del tren la Fig. 6.23 para que cuando se active un pulsador (señal \(P_{on}\)) el tren vaya del punto A al punto B y vuelva a A. Para ello se dispone de dos sensores de fin de carrera en A (señal ‘A’) y en B (señal ‘B’). Para mover el tren se dispone de dos señales: ‘yI’ para mover el tren hacia la izquierda e ‘yD’ para mover el tren hacia la derecha.

Figura 6.23: Sistema de control de una vagoneta

Vamos a proceder con un diseño con una máquina de Moore, es decir, un estado por cada acción de control (o combinaciones de acciones de control). Consideramos los siguientes estados:

• mR: Reposo
• mD: tren moviéndose hacia la derecha
• mI: tren moviéndose hacia la izquierda

Figura 6.24: Máquina de estados del sistema de control de una vagoneta

Para generar la tabla de transición de estados se sigue el proceso siguiente. En primer lugar se rellenan las celdas que corresponden con la activación de estados (y que darán lugar a ecuaciones de activación), obteniendo la Tabla 6.26.

Tabla 6.26: Vagoneta: Tabla de transición de estados rellena con celdas de activación de estados futuros.

m \ PonAB	000	001	010	011	100	101	110	111	O
mR				x			mD	x	0,0
mD		mI		x		mI		x	1,0
mI			mR	x			mR	x	0,1

Las ‘x’ representan celdas que son físicamente imposibles de acuerdo con la descripción del problema. Consecuentemente, pueden tomar el valor de cualquier estado. En este caso, por la distribución física de los sensores, es imposible que las señales A y B estén activas a la vez.

Cada estado en una celda de la tabla genera un minitérmino de la ecuación de activación de dicho estado. Este término contiene el estado (origen) que aparece en la cabecera de la fila de la celda, junto a los literales (combinación de entradas) que figuran en la columna de la celda. En el ejemplo de la Tabla 6.26, cada una de las dos celdas en donde aparece el estado mR produce un minitérmino en la ecuación de activación de dicho estado.

Como siempre, cada ecuación de activación del estado puede simplificarse. La Fig. 6.25 muestra las tablas de Karnaugh correspondiente a la activación de cada uno de los estados. A modo de ejemplo, la tabla de Karnaugh para la activación del estado mD (en rojo) muestra un ‘1’ para la combinación de entradas que hacen que se pase de mR a mD, un ‘0’ en caso contrario y un ’*’ para los casos imposibles o indiferentes. En azul tendremos la combinación de entradas que hacen que se pase de mD a mI (y que por tanto activarán mI). Y en verde la combinación de entradas que hacen que se pase de mI a mR (y que por tanto activarán mR).

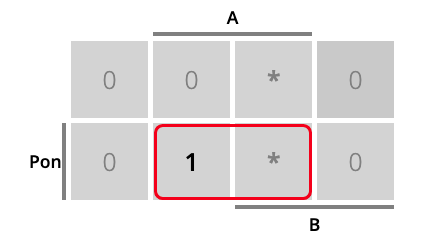
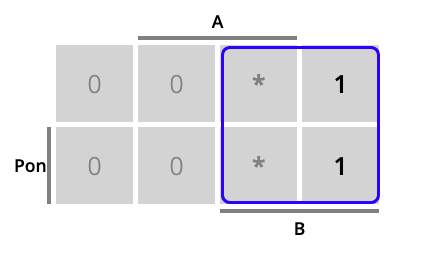
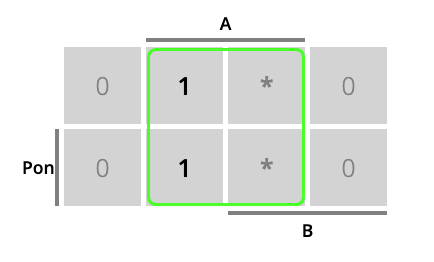
Figura 6.25: Vagoneta: tablas de Karnaugh para el cálculo de las ecuaciones de activación de mR (en verde), mD (en rojo) y mI (en azul)

De cada tabla de Karnaugh obtenemos la ecuación de activación de cada estado:

\[\begin{equation} \begin{aligned} mD_{k+1} &= mR_k · P_{on} · A \\ mI_{k+1} &= mD_k · B \\ mR_{k+1} &= mI_k · A \end{aligned} \tag{6.7} \end{equation}\]

El siguiente paso es completar la Tabla 6.26 con las ecuaciones de retención de los estados. Cada celda que falta por rellenar se corresponde a combinaciones de entradas (columna) que no cambian el estado (fila). La Tabla 6.27 muestra sólo las celdas de retención.

Tabla 6.27: Vagoneta: Tabla de transición de estados para celdas de retención de estados.

m \ PonAB	000	001	010	011	100	101	110	111	O
mR	mR	mR	mR	x	mR	mR		x	0,0
mD	mD		mD	x	mD		mD	x	1,0
mI	mI	mI		x	mI	mI		x	0,1

Nota.- En algunas celdas se podría elegir entre mR o x(*) indistintamente. Corresponde al diseñador elegir lo que sea más acorde a la funcionalidad empleada. Por ejemplo, estando en el estado mR no se debería activar B, por lo que se podría poner x en la fila “001”.

Las ecuaciones de retención pueden obtenerse y simplificarse de una manera similar a las ecuaciones de activación. Con esta metodología, cada ecuación de retención estará formada por un minitérmino compuesto del estado actual y las combinaciones de entradas que no provoquen un cambio de estado. La Fig. 6.26 muestra el caso de mR. Un ‘1’ supone una combinación de entradas que no provoca cambio de estado, un ‘0’ lo contrario y un ’*’ los casos imposibles o indiferentes.

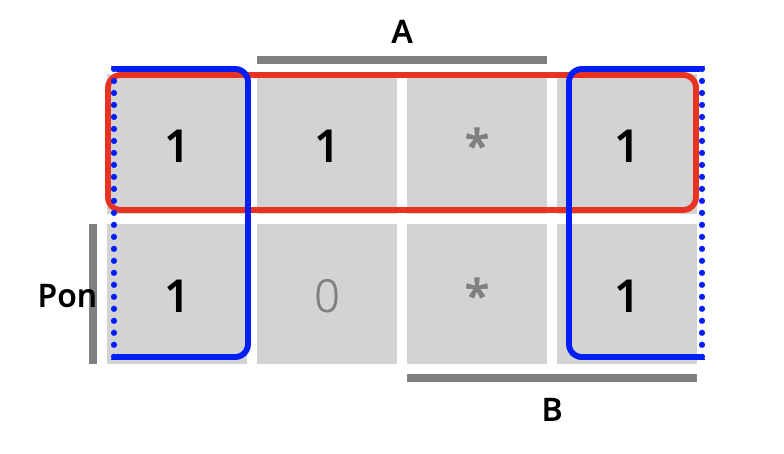
Figura 6.26: Vagoneta: tablas de Karnaugh para el cálculo de las ecuaciones de retención de mR

La ecuación correspondiente será:

\[mR_{k+1} = mR_k · (\overline{A} + \overline{P_{on}})\]

En programas de control reales, no se usan estas ecuaciones para implementar la retención debido al elevado número de entradas de estos sistemas, que llevan a una explosión combinatoria de términos. En la práctica, y tal y como se comentó en la sección 6.2.2, se razona con los estados futuros inmediatos del estado a retener. A modo de ejemplo, se “retiene” el estado mR mientras no se active el estado mD, único estado alcanzable desde mR. La ecuación de retención toma la forma:

\[mR_{k+1} = mR_k · \overline{mD_{k+1}}\]

Ambas tipos de ecuaciones de retención son equivalentes en la práctica.

Ejercicio.- Se deja al lector el cálculo de las ecuaciones de retención de los estados mD y mI.

 

Combinando ambas tablas se obtiene la tabla completa, mostrada en la Tabla 6.28.

Tabla 6.28: Vagoneta: Tabla de transición de estados completa.

m \ P{on}AB	000	001	010	011	100	101	110	111	O
mR	mR	mR	mR	x	mR	mR	mD	x	0,0
mD	mD	mI	mD	x	mD	mI	mD	x	1,0
mI	mI	mI	mR	x	mI	mI	mR	x	0,1

Y combinando las ecuaciones de activación y retención obtenemos las ecuaciones completas, que describen la función de transición entre estados (y cuarto elemento de la 5-tupla de la máquina de estados) delta.

\[\begin{equation} \begin{aligned} mD_{k+1} &= mR_k · Pon · A + mD_k · \overline{mI_{k+1}} \\ mI_{k+1} &= mD_k · B + mI_k · \overline{mR_{k+1}} \\ mR_{k+1} &= mI_k · A + mR_k · \overline{mD_{k+1}} \end{aligned} \tag{6.8} \end{equation}\]

Finalmente, las ecuaciones de las salidas son las siguientes:

\[\begin{equation} \begin{aligned} yI_k &= mI_k \\ yD_k &= mD_k \end{aligned} \tag{6.9} \end{equation}\]

6.6.4 Control de tráfico en un sentido

Se quiere diseñar una máquina de estados que permita detectar vehículos que circulan en dirección contraria por una carretera. Dicho sistema tendrá dos entradas e₁ y e₂ que serán las señales de dos células fotoeléctricas. Dependiendo del orden de activación de dichas señales se podrá detectar si el vehículo circula en sentido correcto o no. En la Fig. 6.27 se puede observar una simulación. Se estudiarán dos casos: en el A, las células fotoeléctricas estarán situadas a una distancia menor que la longitud del vehículo y la separación entre vehículos; en el B, las células fotoeléctricas estarán situadas a una distancia mayor que la longitud del vehículo y menor que la separación entre vehículos.

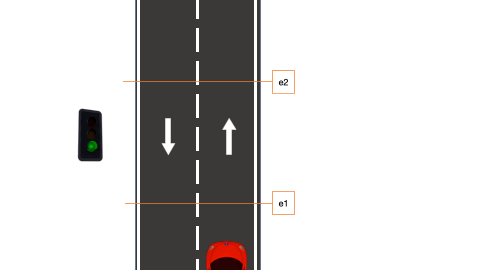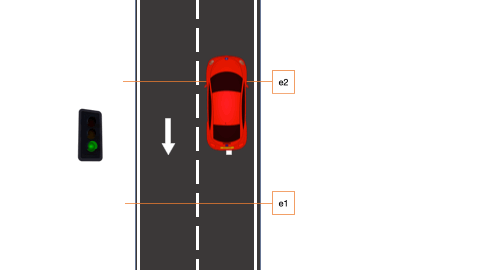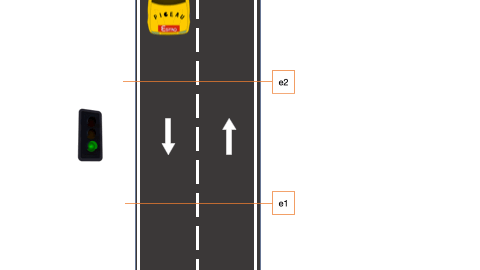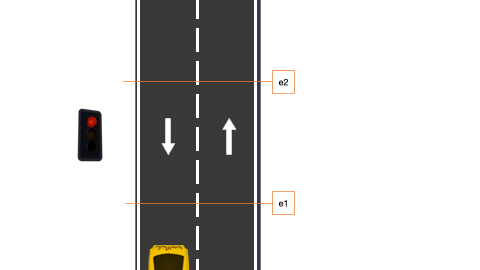
Figura 6.27: Control de tráfico en un sentido (simulación)

6.6.4.1 Control de tráfico en un sentido: caso A

Como se ha indicado, en este caso las señales de las células fotoeléctricas están situadas a una distancia menor que la longitud del vehículo y la separación entre vehículos. En la Fig. 6.28 se puede ver un esquema: si un vehículo circula de forma correcta pasará por los estados m1, m2, m3 y m4. Y si circula de forma incorrecta pasará por los estados m1, m5, m6 y m7.

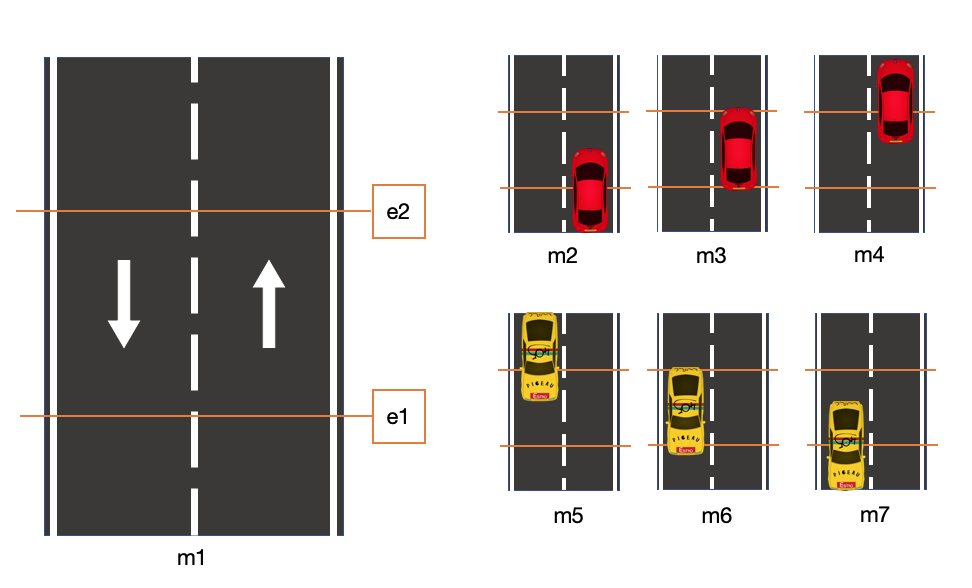
Figura 6.28: Control de tráfico en un sentido (caso A)

Para estos 7 estados, el diagrama de estados de la máquina está dibujado en la Fig. 6.29; la Tabla 6.29 contiene la tabla de transición.

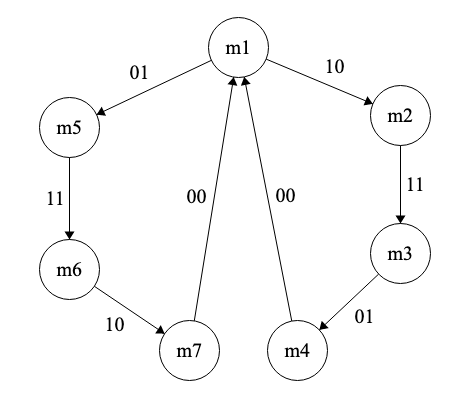
Figura 6.29: Máquina de estados para el control de tráfico en un sentido (caso A)

Tabla 6.29: Control de tráfico: Tabla de transición de estados para el caso A.

m \ e1e2	00	01	10	11	Salida
m1	m1	m5	m2	x	0
m2	X	X	m2	m3	0
m3	X	m4	X	m3	0
m4	m1	m4	X	X	0
m5	X	m5	X	m6	1
m6	X	X	m7	m6	1
m7	m1	X	m7	X	1

Observamos que en este caso es posible simplificar la tabla, fusionando los estados m2, m3 y m4 (en un estado que llamaremos SC, sentido correcto) por un lado, y los estados m5, m6 y m7 (en un estado que llamaremos SI, sentido incorrecto) por otro. A m1 pasaremos a llamarle NO (no hay vehículos).

De esta forma obtenemos la Tabla 6.30.

Tabla 6.30: Control de tráfico: Tabla de transición de estados para el caso A simplificada.

m \ e1e2	00	01	10	11	Salida
NO	NO	SI	SC	x	0
SC	NO	SC	SC	SC	0
SI	NO	SI	SI	SI	1

El diagrama correspondiente queda como indica la Fig. 6.30.

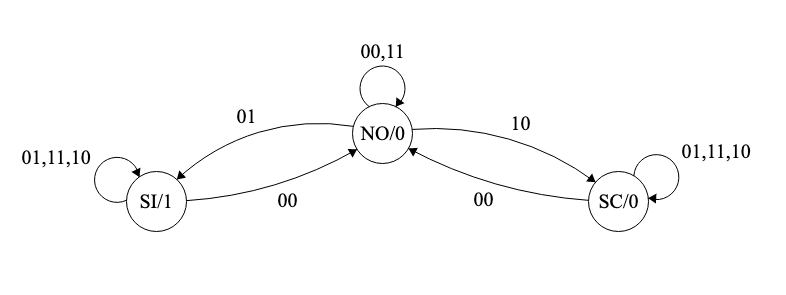
Figura 6.30: Máquina de estados para el control de tráfico en un sentido (caso A)

Y las ecuaciones correspondientes (funciones delta y lambda) de la forma:

\[\begin{equation} \begin{aligned} NO_{k+1} &=(SC_k + SI_k) · \overline{e_1} · \overline{e_2} + NO_k · (\overline{SI_{k+1}+SC_{k+1}}) \\ SC_{k+1} &= NO_k · e_1 + SC_k · \overline{NO_{k+1}} \\ SI_{k+1} &= NO_k · e_2 + SI_k · \overline{NO_{k+1}} \\ Salida_k &= SI_k \end{aligned} \tag{6.10} \end{equation}\]

6.6.4.2 Control de tráfico en un sentido: caso B

Queremos ahora diseñar una máquina de estados que permita detectar vehículos que circulan en dirección contraria por una autovía, pero las células fotoeléctricas estarán ahora situadas a una distancia mayor que la longitud del vehículo y menor que la separación entre vehículos (ver Fig. 6.31).

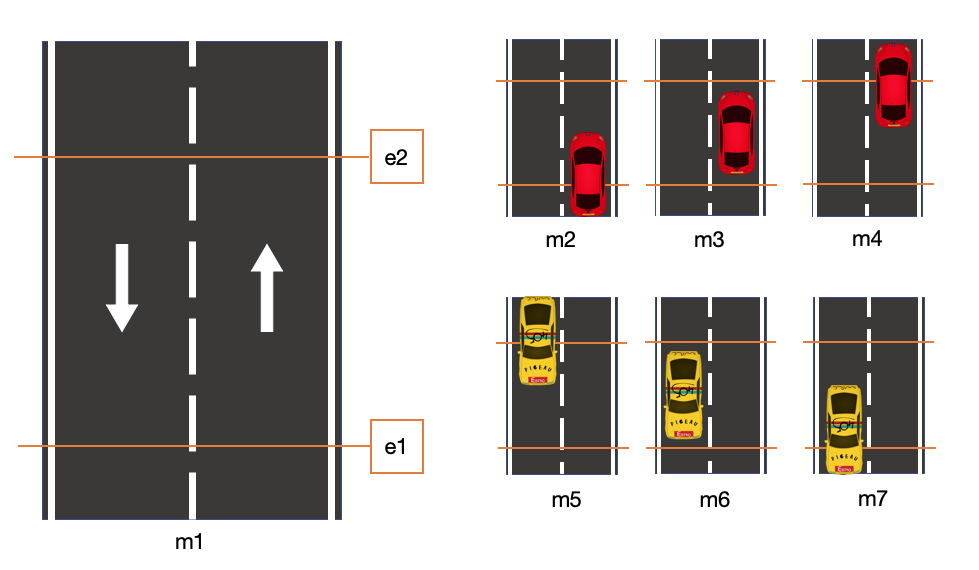
Figura 6.31: Control de tráfico en un sentido (caso B)

Lo primero que se podría pensar es en utilizar el mismo modelo de antes. Obtendríamos la siguiente máquina de estados (Fig. 6.32):

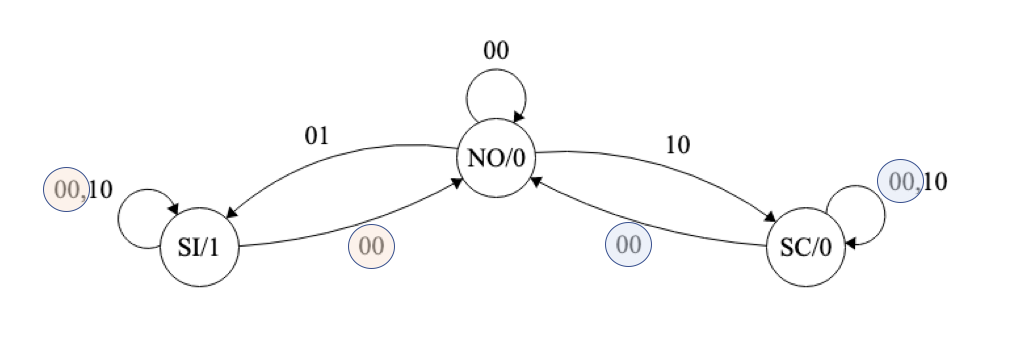
Figura 6.32: Máquina de estados para el control de tráfico en un sentido (caso B): diseño inicial

Podemos observar que no es una máquina correcta. En los estados SC o SI, para las entradas “00” la máquina debería poder evolucionar a dos estados distintos, lo que no es posible pues hablamos siempre de máquinas deterministas. Esta máquina no es, por tanto, suficientemente expresiva, ya que en SC o SI las entradas “00” podrían ser debidas a que el coche está entre los dos sensores o bien a que el coche ha salido del sistema de detección.

Está claro que se necesitan más estados. Vamos a añadir dos estados más:

• NO: no vehículo
• SC: sentido correcto
• SI: sentido incorrecto
• VEC: vehículo entre sensores correcto
• VEI: vehículo entre sensores no correcto

Para estos cinco estados obtenemos la tabla de transición mostrada en la Tabla 6.31:

Tabla 6.31: Control de tráfico: Tabla de transición de estados para el caso B considerando 5 estados.

m \ e1e2	00	01	10	11	Salida
NO	NO	SI	SC	x	0
SC	VEC	SC	SC	x	0
SI	VEI	SI	SI	x	1
VEI	VEI	x	SI	x	1
VEC	VEC	SC	x	x	0

La casilla que está en negrita presenta un un nuevo problema. Vamos a analizarlo con el siguiente diagrama (se representa sólo una parte del diagrama):

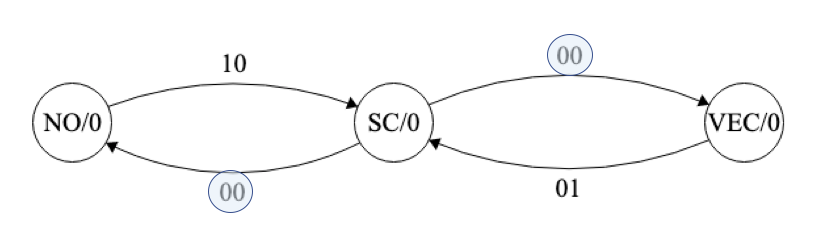
Figura 6.33: Máquina de estados para el control de tráfico en un sentido (caso B): diseño intermedio

Vemos que se vuelve a dar el mismo problema de antes: desde el estado SC salen dos arcos con los mismos valores de entradas (correspondiente al caso de coche no detectado), por lo que no es consistente. Esto quiere decir que, o bien no hemos elegido bien los estados, o necesitamos más de 5 estados. Puesto que el tanteo previo ha sido infructuoso, pasamos ahora a diseñar la máquina con los siete estados intuitivos con semántica de entrada, para luego buscar una simplificación correcta:

• NO: no vehículo
• SC-10: sentido correcto después de detección por parte de e₁
• SC-00: sentido correcto entre sensores
• SC-01: sentido correcto después de detección por parte de e₂
• SI-01: sentido incorrecto después de detección por parte de e₂
• SI-00: sentido incorrecto entre sensores
• SI-10: sentido incorrecto después de detección por parte de e₁

La tabla de transición de estados que obtenemos es la mostrada en la Tabla 6.32.

Tabla 6.32: Control de tráfico: Tabla de transición de estados para el caso B considerando 7 estados.

m \ e1e2	00	01	10	11	Salida
NO	NO	SI-01	SC-10	x	0
SC-10	SC-00	x	SC-10	x	0
SC-00	SC-00	SC-01	x	x	0
SC-01	NO	SC-01	x	x	0
SI-01	SI-00	SI-01	x	x	1
SI-00	SI-00	x	SI-10	x	1
SI-10	NO	x	SI-10	x	1

Vemos que esta tabla es simplificable: se pueden simplificar los estados SC-10 con el SC-00, y el SI-01 con el SI-00. La nueva tabla simplificada se muestra en la Tabla 6.33.

Tabla 6.33: Control de tráfico: Tabla de transición de estados para el caso B final simplificada.

m \ e1e2	00	01	10	11	Salida
NO	NO	SI-01/00	SC-10/00	x	0
SC-10/00	SC-10/00	SC-01	SC-10/00	x	0
SC-01	NO	SC-01	x	x	0
SI-01/00	SI-01/00	SI-01	SI-10	x	1
SI-10	NO	x	SI-10	x	1

Podemos asignar nuevos nombre para entenderlo mejor: SCA será SC-10/00, SCB será SC-01, SIA será SI-01/00 y SIB será SI-10.

Tabla 6.34: Control de tráfico: Tabla de transición de estados para el caso B final simplificada con nuevos nombres.

m \ e1e2	Nuevo Nombre	00	01	10	11	Salida
NO	NO	NO	SIA	SCA	x	0
SC-10/00	SCA	SCA	SCB	SCA	x	0
SC-01	SCB	NO	SCB	x	x	0
SI-01/00	SIA	SIA	SIA	SIB	x	1
SI-10	SIB	NO	x	SIB	x	1

Vemos, por tanto, que cinco estados son suficientes para modelar el sistema. Las ecuaciones de la máquina son:

\[\begin{equation} \begin{aligned} NO_{k+1} &= (SCB + SIB) · (\overline{e_1}· \overline{e_2}) + NO_k · (\overline{SCA_{k+1} + SIA_{k+1}}) \\ SCA_{k+1} &= NO_k · e_1 + SCA_k · \overline{SCB_{k+1}} \\ SCB_{k+1} &= SCA_k · e_2 + SCB_k · \overline{NO_{k+1}} \\ SIA_{k+1} &= NO_k · e_2 + SIA_k · \overline{SIB_{k+1}} \\ SIB_{k+1} &= SIA_k · e_1 + SIB_k · \overline{NO_{k+1}} \\ Salida_k &= SIA_k + SIB_k \end{aligned} \tag{6.11} \end{equation}\]

Y el diagrama de estados se muestra en la Fig. 6.34.

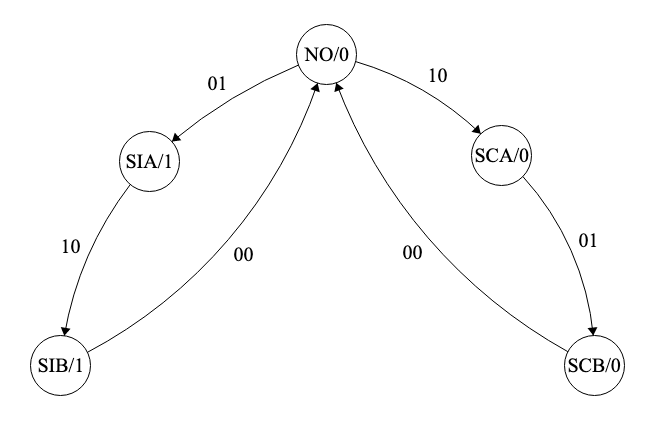
Figura 6.34: Máquina de estados para el control de tráfico en un sentido (caso B): diseño final