6.1 Introducción
Según lo expuesto al comienzo del capítulo 5, se denomina sistema combinacional o lógica combinacional a todo sistema digital en el que sus salidas son función exclusiva del valor de sus entradas en un momento dado, sin que intervengan en ningún caso estados anteriores de las entradas o de las salidas. Las funciones booleanas –compuestas por operadores OR, AND, NAND, XOR– se pueden representar íntegramente mediante una tabla de la verdad. Por tanto, carecen de memoria y de retroalimentación.
A diferencia de los sistemas combinacionales, en los sistemas secuenciales los valores de las salidas en cada instante de tiempo no dependen exclusivamente de los valores de las entradas en dicho momento, sino también dependen del estado anterior o estado interno. El sistema secuencial requiere de la utilización de un dispositivo de memoria que pueda almacenar la historia pasada de sus entradas (denominadas variables de estado) y le permita mantener su estado durante algún tiempo. Estos dispositivos de memoria pueden ser sencillos como un biestable, un relé o una celda de memoria.
El 99.9 % de los sistemas que son útiles en la práctica son secuenciales. Los sistemas combinacionales pueden verse como un caso particular de los sistemas secuenciales. O, de otra forma, los sistemas secuenciales se pueden ver como la suma de un sistema combinacional más un conjunto de memorias (biestables) que actúan como estados.
Formalmente, dado un sistema secuencial discreto formado por n entradas y m salidas y que admite un modelo de máquina de estados finita formado por q estados internos, la relación en el instante de tiempo k entre las entradas y las salidas puede expresarse mediante la función siguiente:
\[Y_k= f(X_k,M_k) \mbox{ donde |X| = n, |Y| = m , |M| = q}\]
Asimismo, la dinámica del sistema viene determinado por la evolución de sus estados. Sea \(M_{k+1}\) la codificación del estado en el instante k+1. La dinámica del sistema puede expresarse mediante la función:
\[M_{k+1}= f(X_k,M_k)\]
En otras palabras, la dinámica depende de las entradas y del estado del sistema en el instante anterior, pero no de las salidas. El resto del capítulo estudia en detalle el modelo de máquina de estado finita para describir a los sistemas secuenciales.
6.1.1 Ejemplo de sistema secuencial
Se dispone de dos pulsadores: P1 (ENCENDIDO) y P2 (APAGADO). Si se pulsa P1 se enciende una luz L (y se mantiene encendida indefinidamente). Si se pulsa P2 la luz se apaga. Si ambos pulsadores están activados, la luz se apaga (parada PREFERENTE). Ver Fig. 6.1.
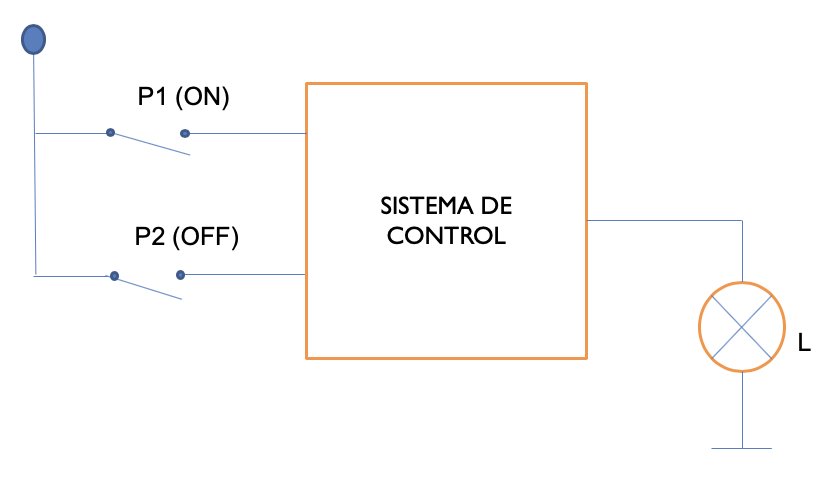
Figura 6.1: Ejercicio de interruptores
Para resolver el ejercicio podríamos pensar en hacer directamente una tabla de verdad (Tabla 6.1):
| P1 | P2 | Salida |
|---|---|---|
| 0 | 0 | ¿0/1? |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Parece claro que cuando se pulse P1 la luz debe encenderse, cuando se pulsa P2 debe apagarse y cuando se pulsen las dos también apagarse. Pero, ¿qué debe ocurrir cuando no se pulse ningún pulsador? Si ponemos un 0 en la tabla de verdad, cuando pulsemos P1 se encenderá la luz pero al soltar el pulsador se apagará (porque hemos puesto un 0 en la primera fila), no quedándose encendida tal y como deseábamos. Por el contrario si ponemos un 1 en la primera fila, al presionar P2 la luz se apagará pero al soltar se volverá a encender. ¿Entonces?
Lo que ocurre es que éste no es un sistema combinacional y por tanto la salida (L) no depende sólo de las entradas. Lo que queremos hacer cuando no se pulse ni P1 ni P2 es mantener el estado. Y, ¿cómo se hace esto? Pues tenemos que definir dos estados. Cuando no se active ningún pulsador, si la luz estaba apagada (estado apagado) seguirá apagada, y si estaba encendida (estado encendido) seguirá encendida.
Para codificar los dos estados es suficiente añadir una única variable booleana m: el valor ‘0’ de la variable representará el estado apagado y el valor ‘1’ el estado encendido.
Y para capturar la dinámica del sistema (la evolución del estado) consideramos dos entradas en la tabla de verdad, el estado en el instante k (mk) y el estado en el instante k+1 (mk+1).
De este modo la tabla de verdad nos quedará de la siguiente forma:
| P1 | P2 | mk | mk+1 | L |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Como puede verse en la Tabla 6.2, la salida L coincide con el valor del estado mk, ya que la semántica del estado coincide con el encendido y apagado de la luz.
La tabla de Karnaugh considerando la variable mk+1 en términos de P1, P2 y mk puede verse en la Fig. 6.2.
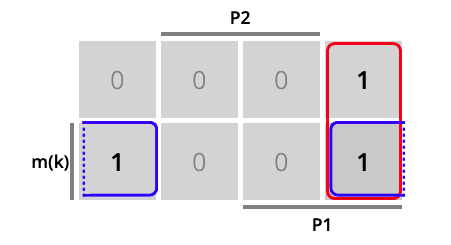
Figura 6.2: Tabla de Karnaugh para el ejercicio de interruptores
A tenor del agrupamiento de minitérminos, la expresión lógica simplificada de mk+1 queda de la siguiente forma:
\[m_{k+1}=\overline{P2_k} · m_k + \overline{P2_k} · P1_k = \overline{P2_k} · (m_k + P1_k)\]
Por último, y según lo expuesto con anterioridad, la expresión de la luz L en función del estado es:
\[L_k = m_k\]
Nota.- Se puede observar como se cumplen las premisas de un sistema secuencial descritas en la Introducción del capítulo: la salida (Lk) depende del estado (mk) (nótese que, en este caso, la salida solo depende del estado), y el estado siguiente (mk+1) depende del estado actual (mk) y de las entradas (\(P1_k\) y \(\overline{P2_k}\)).
Por último, podemos ver una posible implementación en diagrama de contactos en la Fig. 6.3.
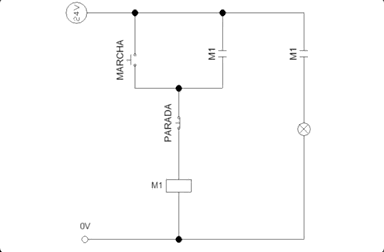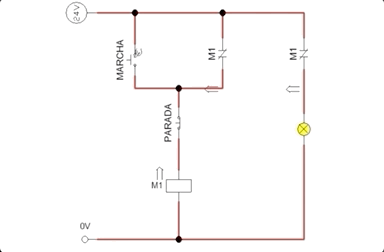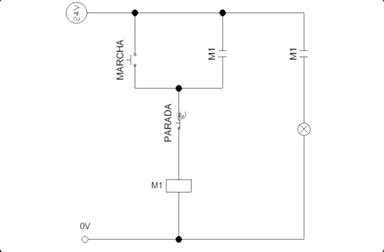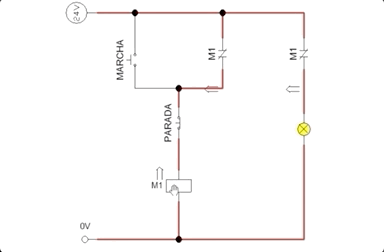
Figura 6.3: Ejemplo de funcionamiento del ejercicio de marcha-paro
Ejercicio.- Identificar a qué variables corresponden en la Fig. 6.3: MARCHA, PARADA y M1.
6.1.2 Tipos de sistemas secuenciales
En este tipo de circuitos entra un factor que no se había considerado en los circuitos combinacionales: el tiempo. Según como manejan el tiempo, los sistemas secuenciales se pueden clasificar en síncronos y asíncronos.
Circuitos secuenciales asíncronos: en los circuitos secuenciales asíncronos, los cambios de estados ocurren al ritmo natural asociado a los elementos que componen el sistema. Esto produce retardos en cascada y puede ocasionar problemas de funcionamiento, ya que estos retardos naturales no están bajo el control del diseñador y además no son idénticos en cada elemento (ej. compuerta lógica).
Circuitos secuenciales síncronos: los circuitos secuenciales síncronos solo permiten un cambio de estado en los instantes marcados o autorizados por una señal de sincronismo de tipo oscilatorio denominada reloj (cristal o circuito capaz de producir una serie de pulsos regulares en el tiempo), lo que soluciona los problemas que tienen los circuitos asíncronos originados por cambios de estado no uniformes dentro del sistema. Los sistemas de control se fundamentan en sistemas secuenciales síncronos.
6.1.3 Máquinas de Moore y de Mealy
Dependiendo de como se obtengan las funciones de salida, los sistemas secuenciales pueden tener dos estructuras denominadas Máquina de Moore y Máquina de Mealy.
Una Máquina de Moore27 es una máquina de estados con la particularidad de que las salidas en un instante dado sólo dependen de los estados en ese instante, es decir:
\[Y_k= f(M_k) \mbox{ donde |X|=n, |Y|=m , |M|=q}\] \[M_{k+1}= f(X_k,M_k)\]
El diagrama de estados para una máquina Moore se representa en la Fig. 6.4:
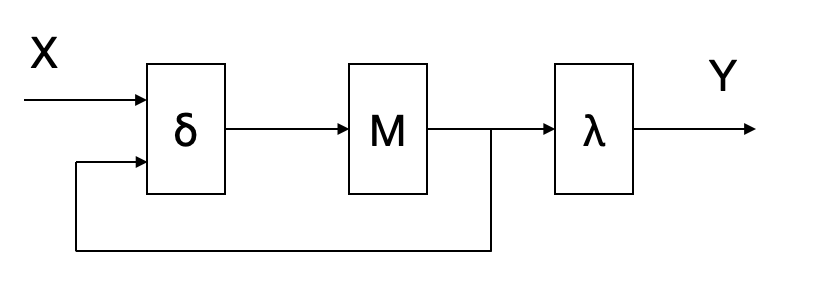
Figura 6.4: Máquina de Moore
Más formalmente, una máquina de estados de tipo Moore es una 5-tupla \(S=(M,X,Y,\delta,\lambda)\) donde:
- \(M \neq \varnothing\) es un conjunto finito de estados
- \(X \neq \varnothing\) es un conjunto finito de entradas
- \(Y \neq \varnothing\) es un conjunto finito de salidas
- \(\delta: M \times X \rightarrow M\) es la función de determina la evolución de los estados
- \(\lambda: M \rightarrow Y\) es la función que determina los valores de las salidas a partir del estado
Obsérvese que la función \(\delta\) determina la evolución del estado, esto es, \(M_{k+1}= \delta(X_k,M_k)\), y la función \(\lambda\) el valor de las salidas, \(Y_k= \lambda(M_k)\). Ambas relaciones representan subsistemas combinacionales dentro del sistema secuencial.
En contraposición con la máquina de Moore, una Máquina de Mealy28 se corresponde con la descripción realizada en la Introducción, esto es, tiene la particularidad de que las salidas dependen tanto del estado como de las entradas en cada instante. Según lo expuesto anteriormente, \(Y_k=f(X_k,M_k )\) y \(M_{k+1}= f(X_k,M_k)\).
El diagrama de estados para una máquina de Mealy se representa en la Fig. 6.5:
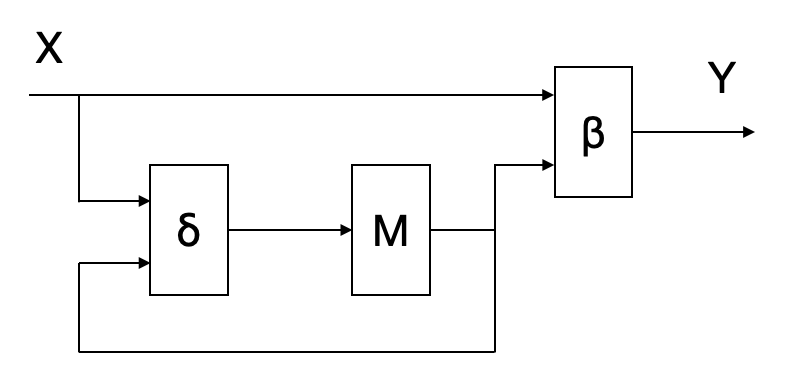
Figura 6.5: Máquina de Mealy
Al igual que en el caso anterior, una Máquina de Mealy puede verse como una 5-tupla \(S=(M,X,Y,\delta,\beta)\) donde:
- \(M \neq \varnothing\) es un conjunto finito de estados
- \(X \neq \varnothing\) es un conjunto finito de entradas
- \(Y \neq \varnothing\) es un conjunto finito de salidas
- \(\delta: M \times X \rightarrow M\) es la función de determina la evolución de los estados
- \(\beta: M \times X \rightarrow Y\) es la función que determina los valores de las salidas a partir del estado y las entradas
Las mismas consideraciones hechas para la máquina de Moore con respecto a las funciones \(\delta\) y \(\lambda\), aplican aquí para las funciones \(\delta\) y \(\beta\).
Es interesante destacar la naturaleza aparentemente generalista de la Máquina de Mealy frente a la Máquina de Moore; al fin y al cabo, la función \(\beta\) es más expresiva que la función \(\lambda\). Sin embargo, y de manera contraintuitiva, existe siempre una conversión entre los dos tipos de máquinas. En el caso general, la conversión de una máquina Mealy a una de Moore conlleva un aumento en el número de estados, según se desprenderá de los ejemplos de la sección 6.6.
Para terminar esta sección se recuerda que la caracterización de una máquina de estados S pasa por definir unívocamente todos y cada uno de los elementos que conforman su 5-tupla.
El nombre “máquina de Moore” viene de su promotor, Edward F. Moore, un pionero de las máquinas de estados, quien escribió Gedanken-experiments on Sequential Machines, pp 129 – 153, Estudios de Autómatas, Anuales de los Estudios Matemáticos, no. 34, Princeton University Press, Princeton, N. J., 1956.”↩︎
El nombre “Máquina de Mealy” viene del promotor del concepto, George H. Mealy, un pionero de las máquinas de estados, quien escribió Un Método para sintetizar Circuitos Secuenciales, Bell System Tech. J. vol 34, pp. 1045–1079, 1955↩︎