Chapter 2 Human brain
This dataset is high-quality and comes from the publication (Gaublomme et al. 2019) using anti–nuclear pore complex antibodies. It includes 2,754 cells from 8 dorsolateral prefrontal cortex donors, 4 females and 4 males.
The subset of hash count data is shown below:
## AAACCTGAGCAGGCTA-1 AAACCTGCACCAGATT-1 AAACCTGGTACTCAAC-1 AAACCTGGTATGCTTG-1 AAACCTGTCTACCAGA-1 AAACCTGTCTGGTATG-1
## S1HuF 35 37 27 46 50 27
## S2HuM 26 28 21 3884 89 22
## S3HuF 37 32 18 14 53 21
## S4HuM 18 21 30 21 80 30
## S5HuF 3267 15 7 8 11 5
## S6HuM 15 3719 8 19 1146 7
## S7HuF 60 53 44 44 76 49
## S8HuM 24 24 1709 39 56 1623
## AAACGGGAGACTACAA-1 AAACGGGAGATGTAAC-1 AAACGGGAGCAATATG-1 AAACGGGCAAGAGGCT-1
## S1HuF 52 39 33 56
## S2HuM 38 32 44 36
## S3HuF 46 14 6684 23
## S4HuM 22 22 44 39
## S5HuF 7 465 9 7
## S6HuM 580 12 16 15
## S7HuF 47 57 75 1034
## S8HuM 31 41 28 54The subset of gene expression data is shown below:
## AAACCTGAGCAGGCTA-1 AAACCTGCACCAGATT-1 AAACCTGGTACTCAAC-1 AAACCTGGTATGCTTG-1 AAACCTGTCTACCAGA-1 AAACCTGTCTGGTATG-1
## RP11-34P13.3 0 0 0 0 0 0
## FAM138A 0 0 0 0 0 0
## OR4F5 0 0 0 0 0 0
## RP11-34P13.7 0 0 0 0 0 0
## RP11-34P13.8 0 0 0 0 0 0
## RP11-34P13.14 0 0 0 0 0 0
## RP11-34P13.9 0 0 0 0 0 0
## FO538757.3 0 0 0 0 0 0
## FO538757.2 1 0 0 0 0 1
## AP006222.2 0 0 0 0 0 0
## AAACGGGAGACTACAA-1 AAACGGGAGATGTAAC-1 AAACGGGAGCAATATG-1 AAACGGGCAAGAGGCT-1
## RP11-34P13.3 0 0 0 0
## FAM138A 0 0 0 0
## OR4F5 0 0 0 0
## RP11-34P13.7 0 0 0 0
## RP11-34P13.8 0 0 0 0
## RP11-34P13.14 0 0 0 0
## RP11-34P13.9 0 0 0 0
## FO538757.3 0 0 0 0
## FO538757.2 0 0 3 0
## AP006222.2 0 0 1 02.1 Local CLR normalization
The first step of CMDdemux is to normalize the hash count data using a local CLR normalization.
## AAACCTGAGCAGGCTA-1 AAACCTGCACCAGATT-1 AAACCTGGTACTCAAC-1 AAACCTGGTATGCTTG-1 AAACCTGTCTACCAGA-1 AAACCTGTCTGGTATG-1
## S1HuF -0.3734377 -0.3367088 -0.2089518 0.02482044 -0.409641487 -0.18887048
## S2HuM -0.6611197 -0.6069991 -0.4501138 4.43955110 0.158342550 -0.38558077
## S3HuF -0.3193704 -0.4777874 -0.5967173 -1.11727696 -0.352483074 -0.43003254
## S4HuM -1.0125176 -0.8832525 -0.1071691 -0.73428471 0.052982035 -0.08708779
## S5HuF 4.1349769 -1.2017062 -1.4617148 -1.62810259 -1.856560470 -1.72931552
## S6HuM -1.1843679 4.2471840 -1.3439317 -0.82959489 2.703437997 -1.44163345
## S7HuF 0.1539173 0.0146891 0.2655062 -0.01866467 0.002338302 0.39094802
## S8HuM -0.7380808 -0.7554191 3.9030923 -0.13644771 -0.298415852 3.87157253
## AAACGGGAGACTACAA-1 AAACGGGAGATGTAAC-1 AAACGGGAGCAATATG-1 AAACGGGCAAGAGGCT-1
## S1HuF 0.17021384 -0.003142928 -0.5712813 0.2527484
## S2HuM -0.13651643 -0.195514820 -0.2909793 -0.1793849
## S3HuF 0.05006953 -0.983972181 4.7099797 -0.6122490
## S4HuM -0.66458386 -0.556528166 -0.2909793 -0.1014234
## S5HuF -1.72063653 2.452163252 -1.7950567 -1.7108613
## S6HuM 2.56467268 -1.127073024 -1.2644285 -1.0177141
## S7HuF 0.07112294 0.368420629 0.2330915 3.1518539
## S8HuM -0.33434217 0.045647237 -0.7303460 0.2170304The output of LocalCLRNorm is a normalized data matrix with rows representing hashtag samples and columns representing cells. Each entry is a normalized value.
2.2 K-medoids clustering
Then K-medoids clustering is performed on the local CLR-normalized data.
We use a box plot to assess whether the chosen number of clusters is appropriate for the data. Each panel represents one hashtag. Ideally, in each panel, a single cluster should show much higher expression of the corresponding hashtag compared with the other clusters. This pattern indicates good clustering.
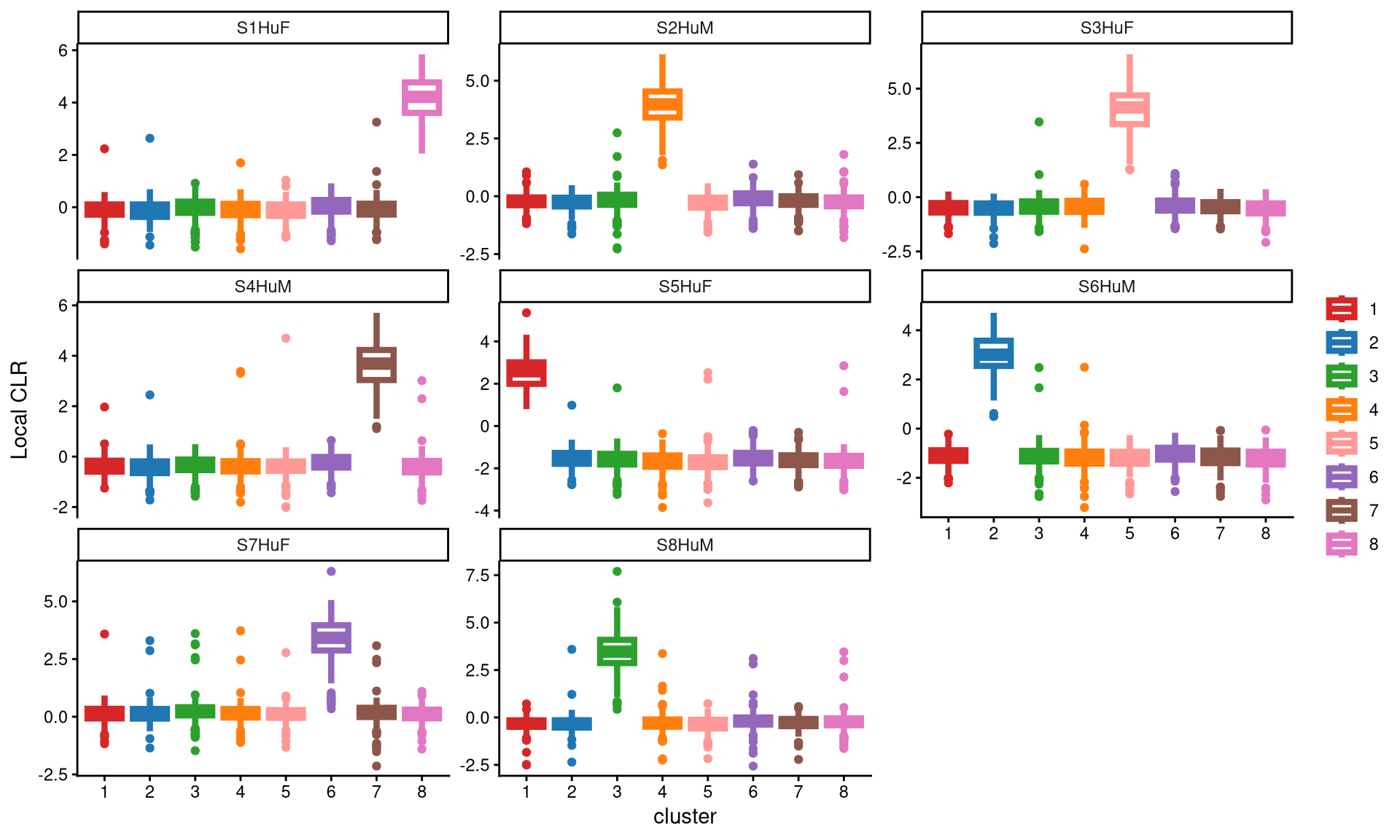
The plots above show that, in each panel, each hashtag is uniquely and highly expressed in a single cluster. This indicates clear clustering and suggests that eight clusters are sufficient for this dataset.
Next, we examine the distribution of the Euclidean distance of each cell to its cluster centroid within each cluster.
2.3 Definition of non-core cells
Core and non-core cells are determined by the DefineNonCore function, which requires the Euclidean distances from the output of the EuclideanClusterDist function and the clustering results from the output of the KmedCluster function. The eu_cut_q parameter can be examined using the EuclideanDistPlot function.
The basic idea for defining non-core cells is that non-core cells are those that have larger Euclidean distances and are farther away from their cluster centroids, whereas core cells are closer to their cluster centroids. A covariance matrix among clusters is required for computing the Mahalanobis distance, and we do not want non-core cells to bias this calculation. Therefore, non-core cells need to be defined in advance.
The distribution of the Euclidean distance to each cell’s cluster centroid is shown in the plot below. In the EuclideanDistPlot function, the length of the vector should match the number of clusters, and each element of the vector represents the cut-off for its corresponding cluster. The cut-off is shown as the red line, and users can adjust the parameter eu_cut_q to select different cut-offs.
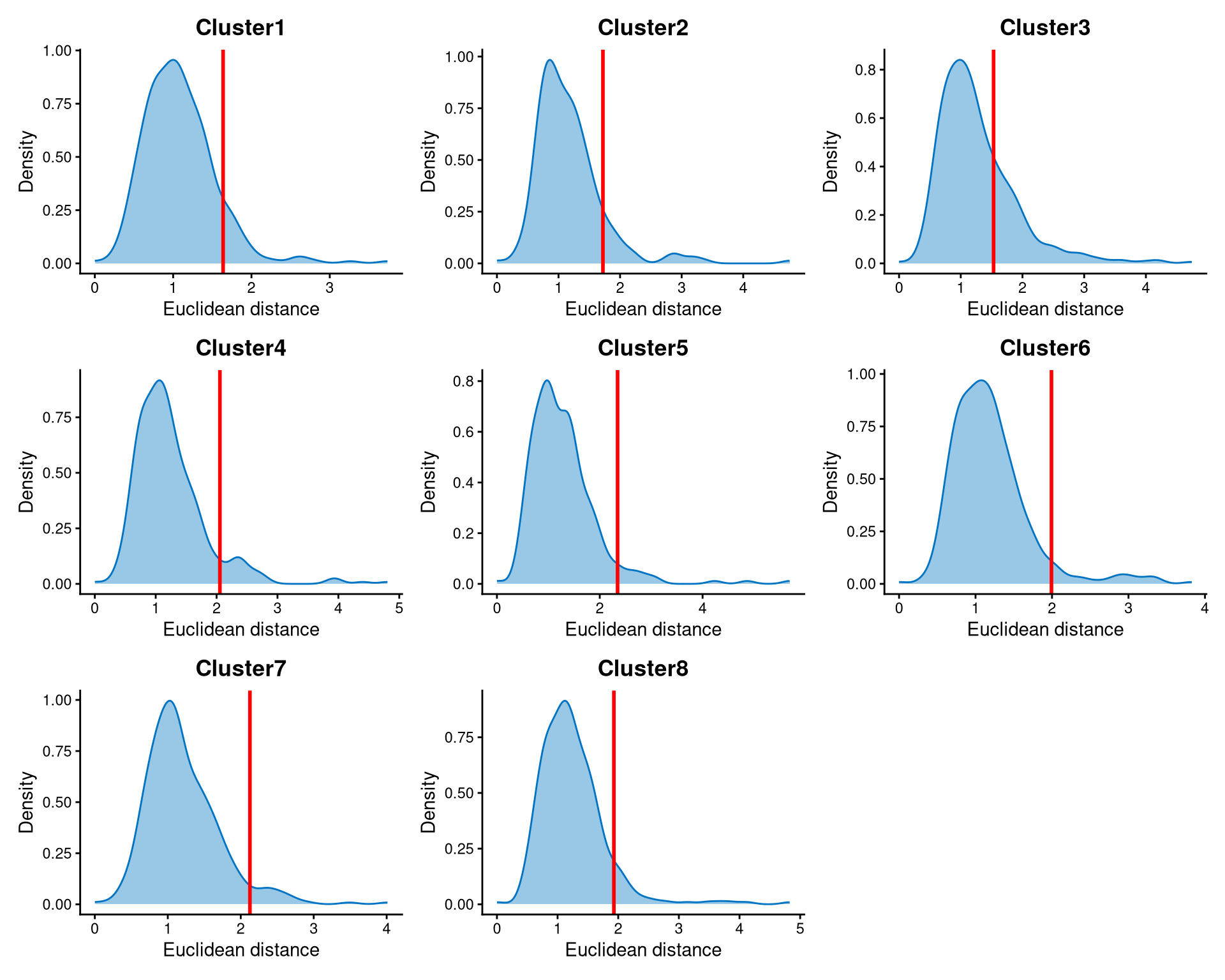
hu.noncore <- DefineNonCore(hu.cl.dist, hu.kmed.cl, eu_cut_q = c(0.9, 0.9, 0.75, 0.92, 0.95, 0.94, 0.95, 0.92))
table(hu.noncore)## hu.noncore
## Cluster1 Cluster2 Cluster3 Cluster4 Cluster5 Cluster6 Cluster7 Cluster8 non-core
## 295 215 340 338 235 384 356 306 285Next, we aim to check the definition of core and non-core cells to determine whether non-core cells are farther from the cluster centroids and core cells are closer to them.
The CLRPlot function requires the CLR-normalized values from LocalCLRNorm, the k-medoids clustering from KmedCluster, and the classified non-core cells from DefineNonCore.
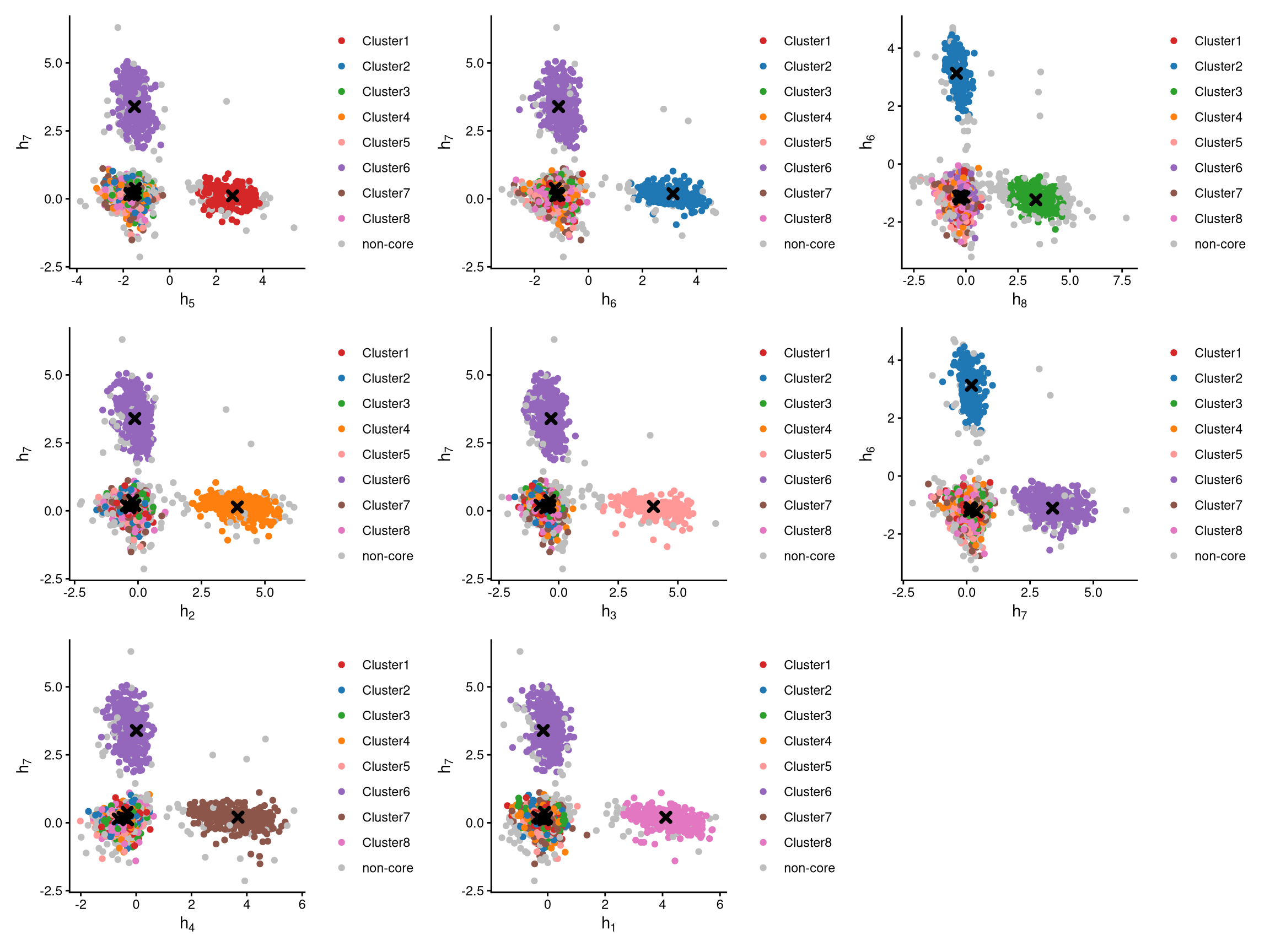
The pairwise CLR-normalized values are shown above. Each plot clearly presents two clusters of cells along with their cluster centroids. The remaining cells are positioned toward the corners. It is evident that core cells are located around the cluster centroid, whereas non-core cells are farther away from it.
2.4 Label clusters by sample
Next, we label each cluster by its original hashtag sample.
The input to LabelClusterHTO requires the CLR-normalized values from LocalCLRNorm, the k-medoids clustering from KmedCluster, and the classified non-core cells from DefineNonCore. For the label_method parameter, we commonly use the default option, but if the default does not work, we recommend using the alternative choice "expression".
hu.cluster.assign <- LabelClusterHTO(hu.clr.norm, hu.kmed.cl, hu.noncore, label_method = "medoids")
hu.cluster.assign## S1HuF S2HuM S3HuF S4HuM S5HuF S6HuM S7HuF S8HuM
## 8 4 5 7 1 2 6 3The output above shows each sample and its corresponding cluster index.
2.5 Computing the Mahalanobis distance
The input to CalculateMD requires the CLR-normalized values from LocalCLRNorm, the k-medoids clustering from KmedCluster, the classified non-core cells from DefineNonCore, and the sample for each cluster from LabelClusterHTO.
## AAACCTGAGCAGGCTA-1 AAACCTGCACCAGATT-1 AAACCTGGTACTCAAC-1 AAACCTGGTATGCTTG-1 AAACCTGTCTACCAGA-1 AAACCTGTCTGGTATG-1
## S1HuF 16.729513 16.734852 15.013791 14.317474 14.03400 14.948725
## S2HuM 16.264356 17.382339 15.166539 2.124494 13.49651 14.998851
## S3HuF 15.974767 15.951861 15.568014 15.512024 13.02795 15.279411
## S4HuM 16.464222 16.245151 13.677554 14.429557 12.04696 13.605766
## S5HuF 3.852669 16.421825 14.443228 14.499488 14.32579 14.757687
## S6HuM 17.021946 3.130796 15.668630 15.655158 2.37060 15.750980
## S7HuF 15.033548 16.005369 12.895535 13.425606 12.88418 12.627110
## S8HuM 16.557064 17.048728 1.747895 14.337369 13.61326 1.663073
## AAACGGGAGACTACAA-1 AAACGGGAGATGTAAC-1 AAACGGGAGCAATATG-1 AAACGGGCAAGAGGCT-1
## S1HuF 13.040572 13.180063 16.869362 11.578491
## S2HuM 13.620153 12.942741 14.834009 12.126149
## S3HuF 12.226865 14.316151 2.128978 12.831285
## S4HuM 12.917871 12.985433 14.676813 11.580369
## S5HuF 13.978824 1.790737 15.299652 12.497210
## S6HuM 1.957518 14.301855 15.290182 13.003293
## S7HuF 12.555800 11.544650 13.810904 1.773481
## S8HuM 13.456450 12.331772 16.092512 10.418022The output of CalculateMD is a matrix of Mahalanobis distances for each cell. Rows of the matrix correspond to hashtags, and columns correspond to cells.
2.6 Detect outlier cells
The outlier cells are defined based on the Mahalanobis distance, so it is necessary to examine the distribution of the Mahalanobis distances and determine an appropriate cut-off.
MDDensPlot is used to visualize the distribution of Mahalanobis distances. The cut-off is determined by md_cut_q, which specifies the quantile of the distribution and is shown in red. In general, we recommend selecting a cut-off near the tail of the distribution, although users can adjust this parameter.
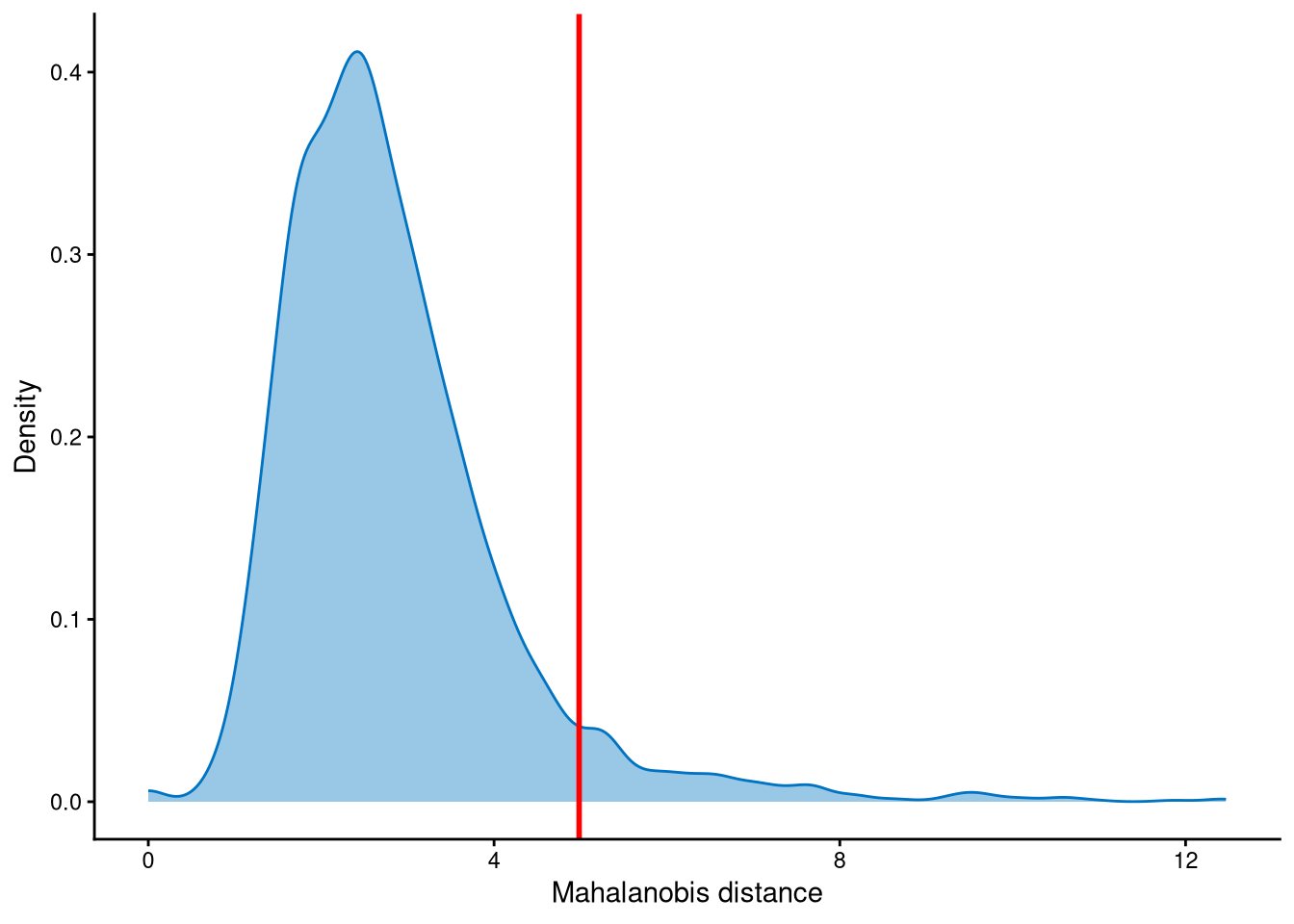
Cells with Mahalanobis distances greater than the cut-off shown in the figure are defined as outliers, whereas the remaining cells are considered singlets.
AssignOutlierDrop requires the Mahalanobis distances from CalculateMD and the md_cut_q value from the above plot to define outlier cells.
## hu.outlier.assign
## Outlier Singlet
## 166 2588The output of AssignOutlierDrop assigns each cell as either “Outlier” or “Singlet”.”
2.7 Demultiplexing
To distinguish negatives and doublets from outlier cells, the distribution of hashtag (HTO) library sizes within outlier cells is visualized using OutlierHTOPlot.
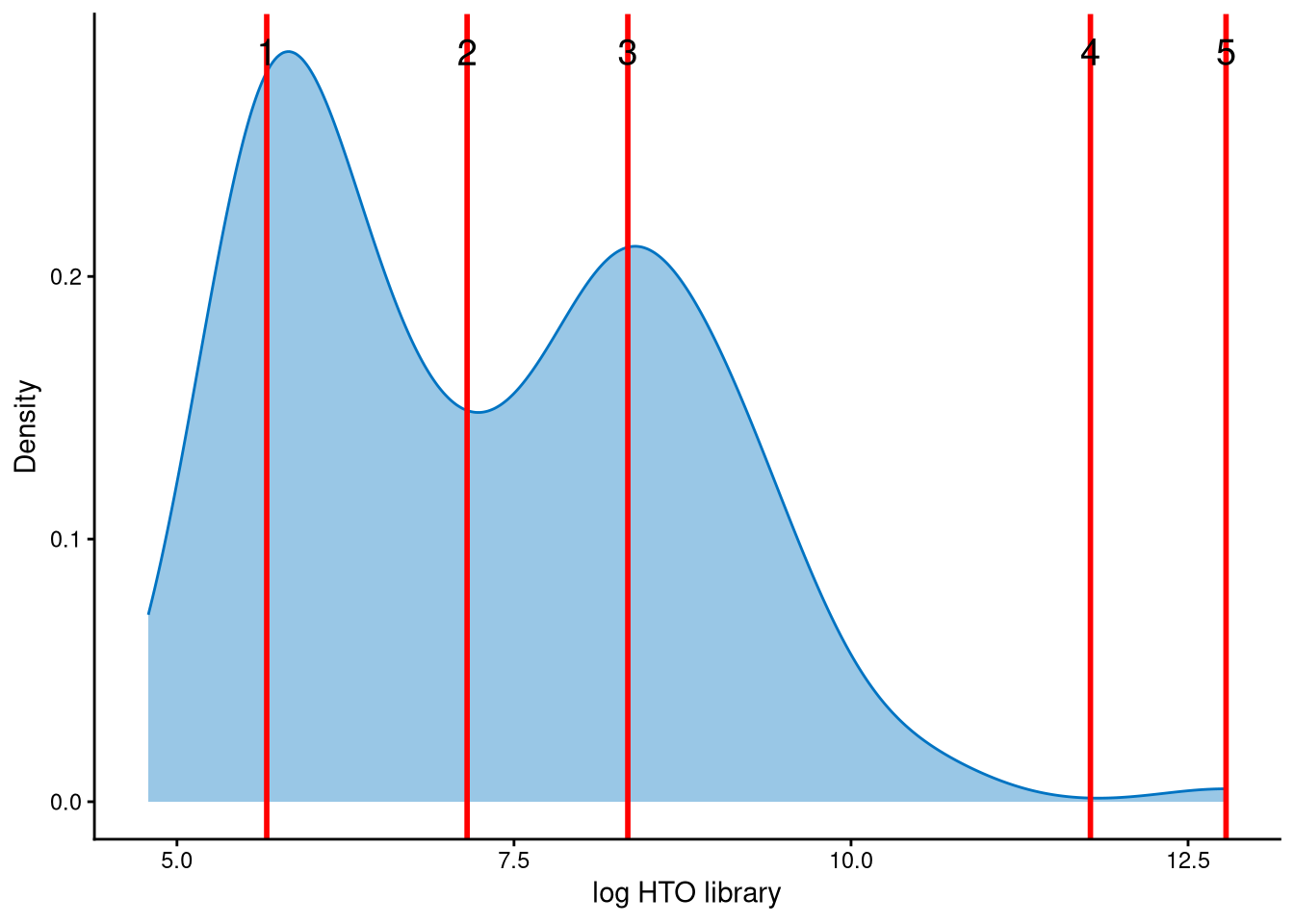
The distribution of HTO library sizes is bimodal. Cells with smaller HTO library sizes are likely negatives, whereas cells with larger HTO library sizes are likely doublets. The red lines in the plots above represent the modes and anti-modes of the distribution, which indicate potential cut-offs. The cut-off between negatives and doublets should be set at the anti-mode between the two peaks, which corresponds to index 2 of the red lines.
The final step is CMDdemux classification. Since this dataset contains gene expression data, we set use_gex_data to TRUE and provide the gene expression count data using the gex.count parameter. The num_modes parameter specifies the number of modes in the distribution, and cut_no specifies the index of the cut-off line. The appropriate number of modes and cut-off position can be determined from the OutlierHTOPlot above. For most high-quality datasets, the default values of num_modes and cut_no are sufficient.
hu.cmddemux.assign <- CMDdemuxClass(hu.md.mat, hu.hash.count, hu.outlier.assign, use_gex_data = TRUE, gex.count = hu.gex.count, num_modes = 3, cut_no = 2)
head(hu.cmddemux.assign)## demux_id global_class demux_global_class doublet_class
## AAACCTGAGCAGGCTA-1 S5HuF Singlet S5HuF S5HuF
## AAACCTGCACCAGATT-1 S6HuM Singlet S6HuM S6HuM
## AAACCTGGTACTCAAC-1 S8HuM Singlet S8HuM S8HuM
## AAACCTGGTATGCTTG-1 S2HuM Singlet S2HuM S2HuM
## AAACCTGTCTACCAGA-1 S6HuM Singlet S6HuM S6HuM
## AAACCTGTCTGGTATG-1 S8HuM Singlet S8HuM S8HuMAn example of the output is shown above.
CMDdemux provides four types of outputs:
demux_id: the identity for each cell, determined by the sample with the minimum Mahalanobis distance for that cell.
global_class: classification of each cell as Singlet, Doublet, or Negative.
demux_global_class: singlet cells are labeled with their original sample, while negatives and doublets are labeled accordingly.
doublet_class: similar to demux_global_class, but doublets are labeled with their sample of origin. This is particularly useful for combined-hashtag experiments.
##
## Doublet Negative S1HuF S2HuM S3HuF S4HuM S5HuF S6HuM S7HuF S8HuM
## 69 82 320 345 230 358 322 227 393 408The output above shows the number of cells demultiplexed into each category.