14.4 非线性规划

开源的非线性优化求解器，推荐使用 nloptr，它支持全局优化，同时推荐 ROI，它有统一的接口函数。

14.4.1 一元非线性优化

下面考虑一个稍微复杂的一元函数优化问题，求复合函数的极值

$g(x) = \int_{0}^{x} -\sqrt{t}\exp(-t^2) \mathrm{dt}, \quad f(y) = \int_{0}^{y} g(s) \exp(-s) \mathrm{ds}$

g <- function(x) {
  integrate(function(t) {
    -sqrt(t) * exp(-t^2)
  }, lower = 0, upper = x)$value
}

f <- function(y) {
  integrate(function(s) {
    Vectorize(g, "x")(s) * exp(-s)
  }, lower = 0, upper = y)$value
}

optimize(f, interval = c(10, 100), maximum = FALSE)

## $minimum
## [1] 66.84459
## 
## $objective
## [1] -0.3201572

计算积分的时候，输入了一系列 s 值，参数是向量，而函数 g 只支持输入参数是单个值，g(c(1,2)) 会报错，因此上面对函数 g() 用了向量化函数 Vectorize() 操作。

g(1)

## [1] -0.453392

类似地，同时计算多个目标函数 f(y) 的值，也需要Vectorize() 实现向量化操作。

Vectorize(f, "y")(c(1, 2))

## [1] -0.1103310 -0.2373865

14.4.2 多元非线性无约束优化

下面这些用来测试优化算法的函数来自维基百科

14.4.2.1 Himmelblau 函数

Himmelblau 函数是一个多摸函数，常用于比较优化算法的优劣。

$f(x_1,x_2) = (x_1^2 + x_2 -11)^2 + (x_1 + x_2^2 -7)^2$ 它在四个位置取得一样的极小值，分别是 $f(-3.7793, -3.2832) = 0$ ， $f(-2.8051, 3.1313) = 0$ ， $f(3, 2) = 0$ ， $f(3.5844, -1.8481) = 0$ 。函数图像见图 14.3。

# 目标函数
fn <- function(x) {
   (x[1]^2 + x[2] - 11)^2 + (x[1] + x[2]^2 - 7)^2
}

df <- expand.grid(
  x = seq(-5, 5, length = 101),
  y = seq(-5, 5, length = 101)
)

df$fnxy = apply(df, 1, fn)

library(lattice)
# 减少三维图形的边空
lattice.options(
  layout.widths = list(
    left.padding = list(x = -.6, units = "inches"),
    right.padding = list(x = -1.0, units = "inches")
  ),
  layout.heights = list(
    bottom.padding = list(x = -.8, units = "inches"),
    top.padding = list(x = -1.0, units = "inches")
  )
)

wireframe(
  data = df, fnxy ~ x * y,
  shade = TRUE, drape = FALSE,
  xlab = expression(x[1]), 
  ylab = expression(x[2]), 
  zlab = list(expression(
    italic(f) ~ group("(", list(x[1], x[2]), ")")
    ), rot = 90),
  shade.colors.palette = custom_palette,
  scales = list(arrows = FALSE, col = "black"),
  par.settings = list(axis.line = list(col = "transparent")),
  screen = list(z = -240, x = -70, y = 0)
)

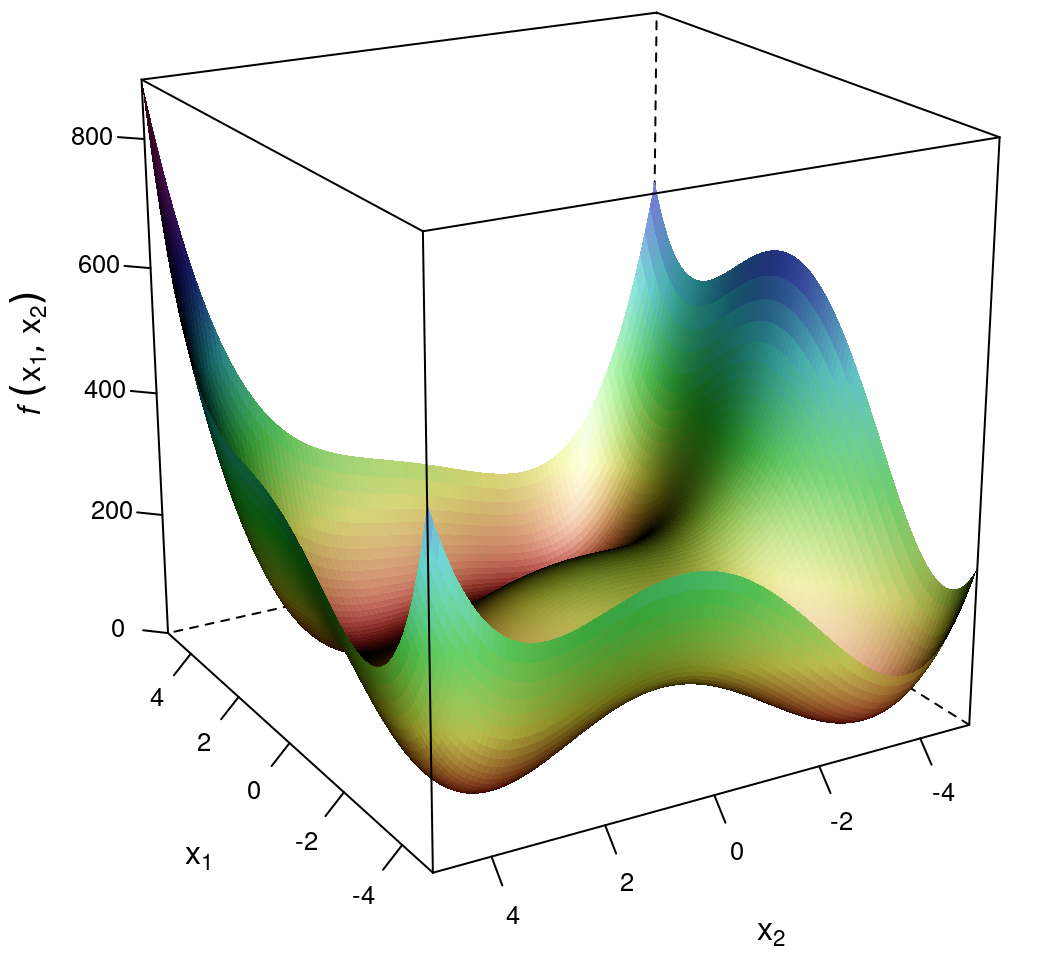
图 14.3: Himmelblau 函数图像

# 梯度函数
gr <- function(x) {
  numDeriv::grad(fn, c(x[1], x[2])) 
}
optim(par = c(-1.2, 1), fn = fn, gr = gr, method = "BFGS")

## $par
## [1] -2.805118  3.131313
## 
## $value
## [1] 2.069971e-27
## 
## $counts
## function gradient 
##       42       15 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

14.4.2.2 Peaks 函数

测试函数

$\begin{aligned} f(x,y) = &~ 3(1-x)\exp\{-x^2 - (y+1)^2\} \\ &- 10(\frac{x}{5} - x^3 - y^5)\exp\{-x^2-y^2\} \\ &- \frac{1}{3}\exp\{-(x+1)^2-y^2\} \end{aligned}$

peaks <- expression(3*(1-x)*exp^(-x^2 - (y+1)^2) - 10*(x/5 - x^3 - y^5)*exp^(-x^2-y^2) -1/3*exp^(-(x+1)^2-y^2))

D(peaks, "x")

## -(3 * (1 - x) * (exp^(-x^2 - (y + 1)^2) * (log(exp) * (2 * x))) + 
##     3 * exp^(-x^2 - (y + 1)^2) + (10 * (1/5 - 3 * x^2) * exp^(-x^2 - 
##     y^2) - 10 * (x/5 - x^3 - y^5) * (exp^(-x^2 - y^2) * (log(exp) * 
##     (2 * x)))) - 1/3 * (exp^(-(x + 1)^2 - y^2) * (log(exp) * 
##     (2 * (x + 1)))))

D(peaks, "y")

## -(3 * (1 - x) * (exp^(-x^2 - (y + 1)^2) * (log(exp) * (2 * (y + 
##     1)))) - (10 * (x/5 - x^3 - y^5) * (exp^(-x^2 - y^2) * (log(exp) * 
##     (2 * y))) + 10 * (5 * y^4) * exp^(-x^2 - y^2)) - 1/3 * (exp^(-(x + 
##     1)^2 - y^2) * (log(exp) * (2 * y))))

library(Deriv)
Simplify(D(peaks, "x"))

## -(10 * ((0.2 - 3 * x^2)/exp^(x^2 + y^2)) + 3/exp^((1 + y)^2 + 
##     x^2) + log(exp) * (x * (6 * ((1 - x)/exp^((1 + y)^2 + x^2)) - 
##     20 * ((x * (0.2 - x^2) - y^5)/exp^(x^2 + y^2))) - 0.666666666666667 * 
##     ((1 + x)/exp^((1 + x)^2 + y^2))))

Simplify(D(peaks, "y"))

## -((6 * ((1 - x) * (1 + y)/exp^((1 + y)^2 + x^2)) - 0.666666666666667 * 
##     (y/exp^((1 + x)^2 + y^2))) * log(exp) - y * (20 * (log(exp) * 
##     (x * (0.2 - x^2) - y^5)/exp^(x^2 + y^2)) + 50 * (y^3/exp^(x^2 + 
##     y^2))))

fn <- function(x) {
  3 * (1 - x[1])^2 * exp(-x[1]^2 - (x[2] + 1)^2) -
    10 * (x[1] / 5 - x[1]^3 - x[2]^5) * exp(-x[1]^2 - x[2]^2) -
    1 / 3 * exp(-(x[1] + 1)^2 - x[2]^2)
}
# 梯度函数
gr <- function(x) {
  numDeriv::grad(fn, c(x[1], x[2]))
}

optim(par = c(-1.2, 1), fn = fn, gr = gr, method = "BFGS")

## $par
## [1] -1.3473958  0.2045192
## 
## $value
## [1] -3.049849
## 
## $counts
## function gradient 
##       28       10 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

在 $(-1.3473958, 0.2045192)$ 处取得极小值

df <- expand.grid(
  x = seq(-3, 3, length = 51),
  y = seq(-3, 3, length = 51)
)

df$fnxy <- apply(df, 1, fn)

wireframe(
  data = df, fnxy ~ x * y,
  shade = TRUE, drape = FALSE,
  xlab = expression(x[1]),
  ylab = expression(x[2]),
  zlab = list(expression(
    italic(f) ~ group("(", list(x[1], x[2]), ")")
  ), rot = 90), aspect = c(1, 0.75), 
  shade.colors.palette = custom_palette,
  scales = list(arrows = FALSE, col = "black"),
  par.settings = list(
    axis.line = list(col = "transparent")
    ),
  screen = list(z = 45, x = -70, y = 0)
)

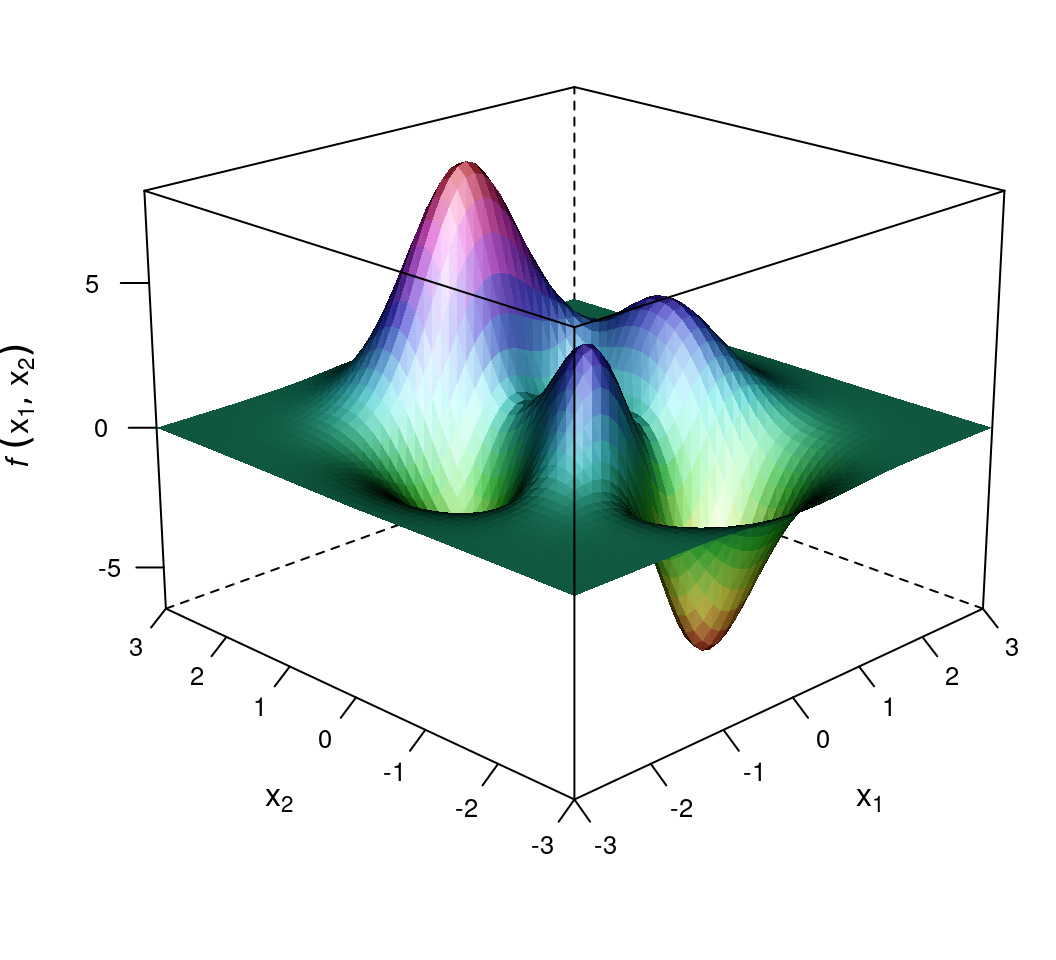
图 14.4: Peaks 多峰图像

函数来自 Octave 内置的 peaks() 函数，它有很多的局部极大值和极小值，可在 Octave Online 上输入命令 help peaks 查看其帮助文档。

14.4.2.3 Rosenbrock 函数

香蕉函数定义如下：

$f(x_1,x_2) = 100 (x_2 -x_1^2)^2 + (1 - x_1)^2$

fn <- function(x) {
  (100 * (x[2] - x[1]^2)^2 + (1 - x[1])^2)
}

df <- expand.grid(
  x = seq(-2.5, 2.5, length = 101),
  y = seq(-2.5, 2.5, length = 101)
)
df$fnxy = apply(df, 1, fn)

wireframe(
  data = df, fnxy ~ x * y,
  shade = TRUE, drape = FALSE,
  xlab = expression(x[1]), 
  ylab = expression(x[2]), 
  zlab = list(expression(italic(f) ~ group("(", list(x[1], x[2]), ")")), rot = 90),
  scales = list(arrows = FALSE, col = "black"),
  par.settings = list(axis.line = list(col = "transparent")),
  screen = list(z = 120, x = -70, y = 0)
)

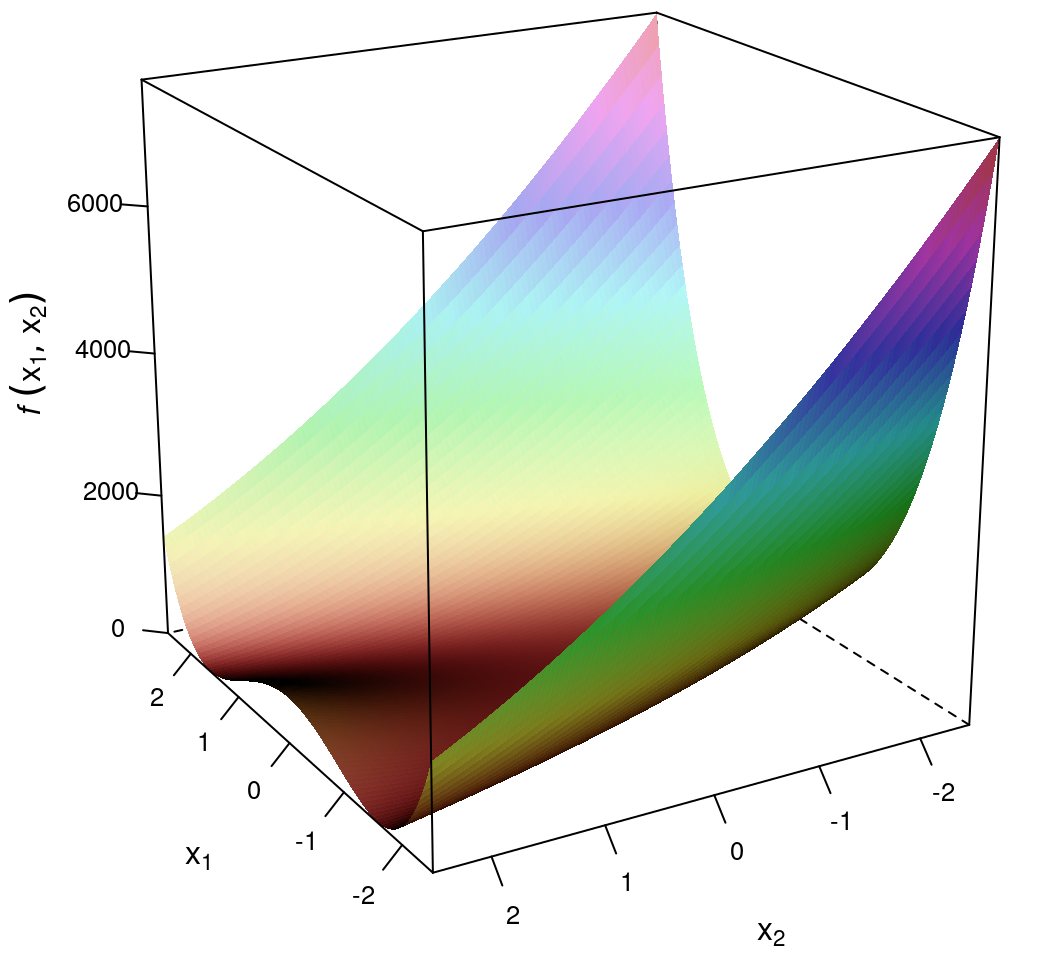
图 14.5: 香蕉函数图像

r <- raster::rasterFromXYZ(df, crs = CRS("+proj=longlat +datum=WGS84"))
rasterVis::vectorplot(r, par.settings = RdBuTheme())

# 梯度函数
gr <- function(x) {
  numDeriv::grad(fn, c(x[1], x[2])) 
}
optim(par = c(-1.2, 1), fn = fn, gr = gr, method = "BFGS")

## $par
## [1] 1 1
## 
## $value
## [1] 9.595012e-18
## 
## $counts
## function gradient 
##      110       43 
## 
## $convergence
## [1] 0
## 
## $message
## NULL

op <- OP(
  objective = F_objective(fn, n = 2L, G = gr),
  bounds = V_bound(ld = -3, ud = 3, nobj = 2L)
)
nlp <- ROI_solve(op, solver = "nloptr.lbfgs", start = c(-1.2, 1))
nlp$objval

## [1] 1.364878e-17

nlp$solution

## [1] 1 1

14.4.2.4 Ackley 函数

Ackley 函数是一个非凸函数，有大量局部极小值点，获取全局极小值点是一个比较有挑战的事。它的 $n$ 维形式如下： $f(\mathbf{x}) = - a \mathrm{e}^{-b\sqrt{\frac{1}{n}\sum_{i=1}^{n}x_{i}^{2}}} - \mathrm{e}^{\frac{1}{n}\sum_{i=1}^{n}\cos(cx_i)} + a + \mathrm{e}$ 其中， $a = 20, b = 0.2, c = 2\pi$ ，对 $\forall i = 1,2,\cdots, n$ ， $x_i \in [-10, 10]$ ， $f(\mathbf{x})$ 在 $\mathbf{x}^{\star} = (0,0,\cdot,0)$ 取得全局最小值 $f(\mathbf{x}^{\star}) = 0$ ，二维图像如图 14.6。

fn <- function(x, a = 20, b = 0.2, c = 2 * pi) {
  mean1 <- mean(x^2)
  mean2 <- mean(cos(c * x))
  -a * exp(-b * sqrt(mean1)) - exp(mean2) + a + exp(1)
}

df <- expand.grid(
  x = seq(-10, 10, length.out = 201),
  y = seq(-10, 10, length.out = 201)
)

df$fnxy = apply(df, 1, fn)

wireframe(
  data = df, fnxy ~ x * y,
  shade = TRUE, drape = FALSE,
  xlab = expression(x[1]), 
  ylab = expression(x[2]), 
  zlab = list(expression(italic(f) ~ group("(", list(x[1], x[2]), ")")), rot = 90),
  scales = list(arrows = FALSE, col = "black"),
  par.settings = list(axis.line = list(col = "transparent")),
  screen = list(z = 120, x = -70, y = 0)
)

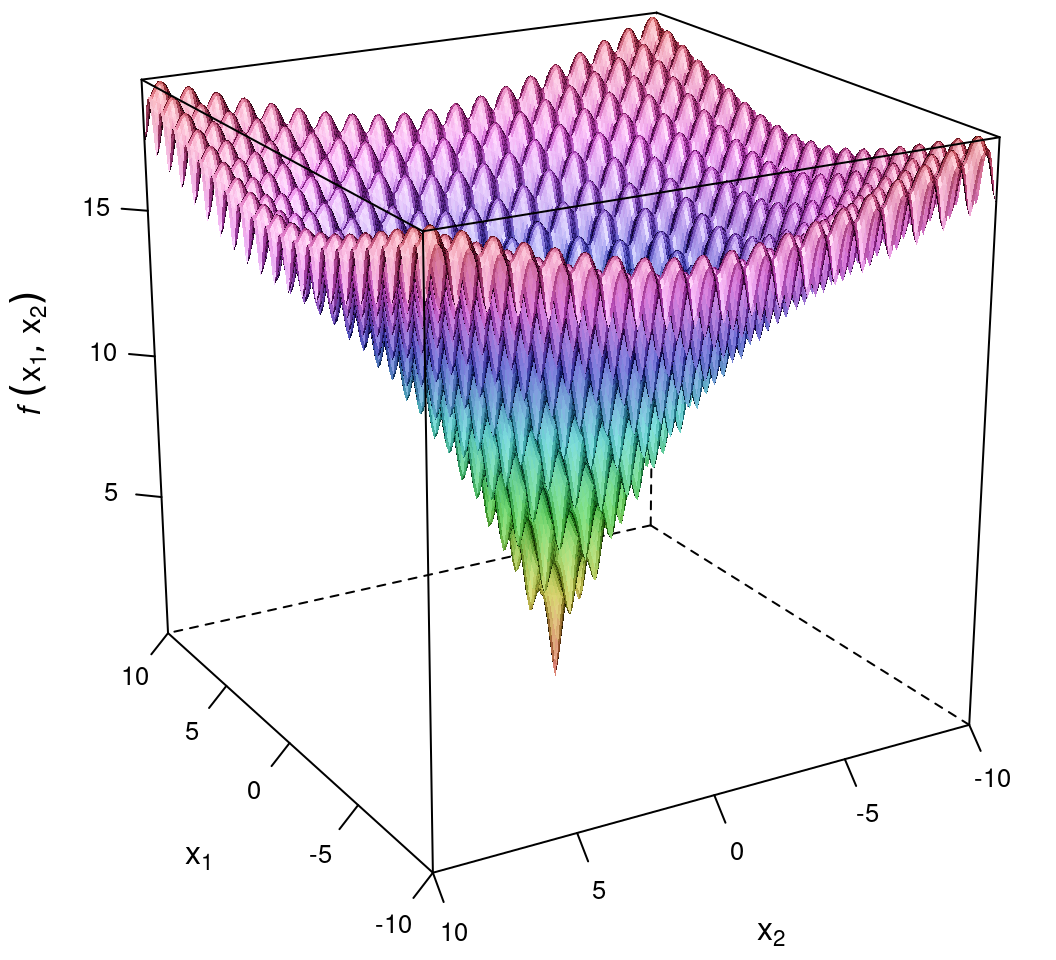
图 14.6: 二维 Ackley 函数图像

以 10 维的 Ackley 函数为例，先试一下普通的局部优化算法 — Nelder–Mead 算法，选择初值 $(2,2,\cdots,2)$ ，看下效果，再与全局优化算法比较。

op <- OP(
  objective = F_objective(fn, n = 10L),
  bounds = V_bound(ld = -10, ud = 10, nobj = 10L)
)

nlp <- ROI_solve(op, solver = "nloptr.neldermead", start = rep(2, 10))
nlp$solution

##  [1] 2 2 2 2 2 2 2 2 2 2

nlp$objval

## [1] 6.593599

可以说完全没有优化效果，已经陷入局部极小值。根据nloptr 全局优化算法的介绍，这里采用 directL 算法，因为是全局优化，不用选择初值。

# 调全局优化器
nlp <- ROI_solve(op, solver = "nloptr.directL")
nlp$solution

##  [1] 0 0 0 0 0 0 0 0 0 0

nlp$objval

## [1] 4.440892e-16

fn(x = c(2, 2))

## [1] 6.593599

fn(x = rep(2, 10))

## [1] 6.593599

14.4.2.5 Schaffer 函数

$f(x_1,x_2) = 0.5 + \frac{\sin^2(x_1^2 - x_2^2) - 0.5}{ [1 + 0.001(x_1^2 + x_2^2)]^2}$

在 $\mathbf{x}^\star = (0,0)$ 处取得全局最小值 $f(\mathbf{x}^\star) = 0$

fn <- function(x) {
  0.5 + ((sin(x[1]^2 - x[2]^2))^2 - 0.5) / (1 + 0.001*(x[1]^2 + x[2]^2))^2
}

df <- expand.grid(
  x = seq(-50, 50, length = 201),
  y = seq(-50, 50, length = 201)
)
df$fnxy = apply(df, 1, fn)

wireframe(
  data = df, fnxy ~ x * y,
  shade = TRUE, drape = FALSE,
  xlab = expression(x[1]), 
  ylab = expression(x[2]), 
  zlab = list(expression(italic(f) ~ group("(", list(x[1], x[2]), ")")), rot = 90),
  scales = list(arrows = FALSE, col = "black"),
  par.settings = list(axis.line = list(col = "transparent")),
  screen = list(z = 120, x = -70, y = 0)
)

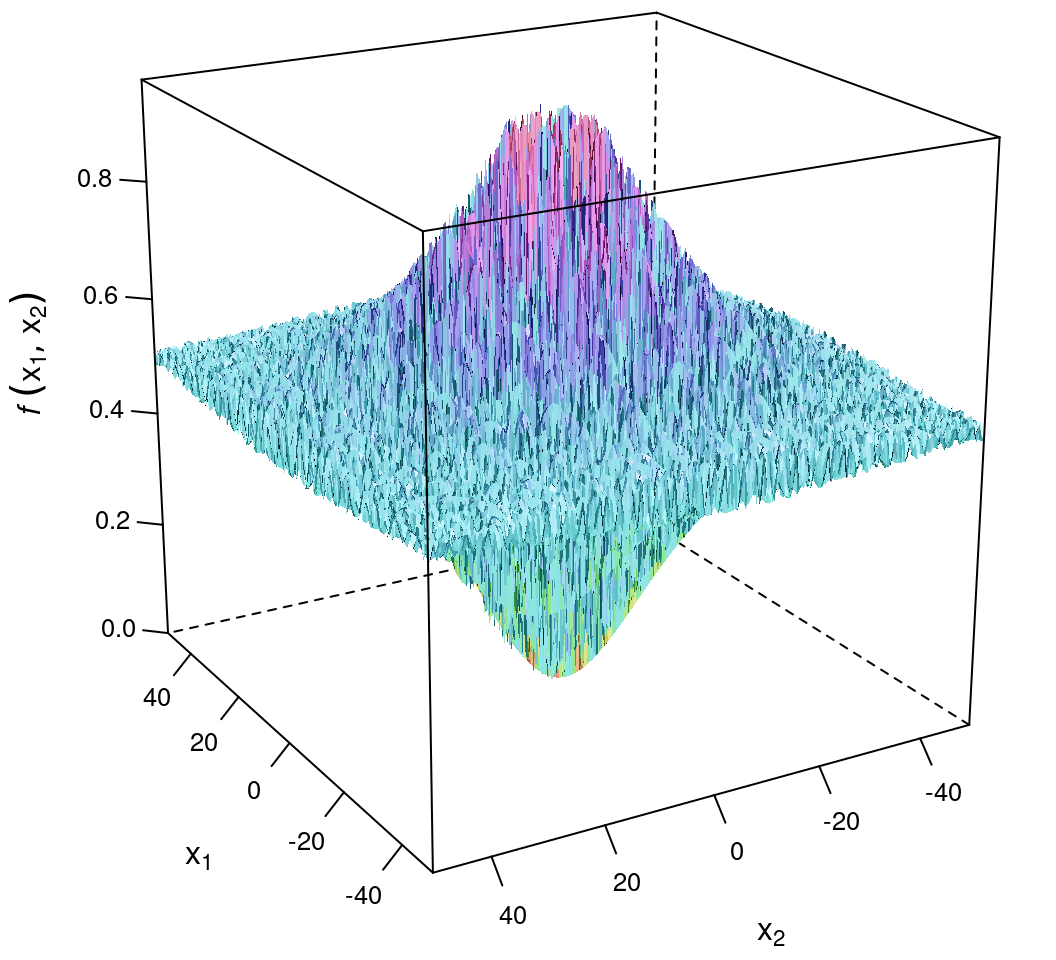
图 14.7: Schaffer 函数

df <- expand.grid(
  x = seq(-2, 2, length = 101),
  y = seq(-2, 2, length = 101)
)
df$fnxy = apply(df, 1, fn)

wireframe(
  data = df, fnxy ~ x * y,
  shade = TRUE, drape = FALSE,
  xlab = expression(x[1]), 
  ylab = expression(x[2]), 
  zlab = list(expression(italic(f) ~ group("(", list(x[1], x[2]), ")")), rot = 90),
  scales = list(arrows = FALSE, col = "black"),
  par.settings = list(axis.line = list(col = "transparent")),
  screen = list(z = 120, x = -70, y = 0)
)

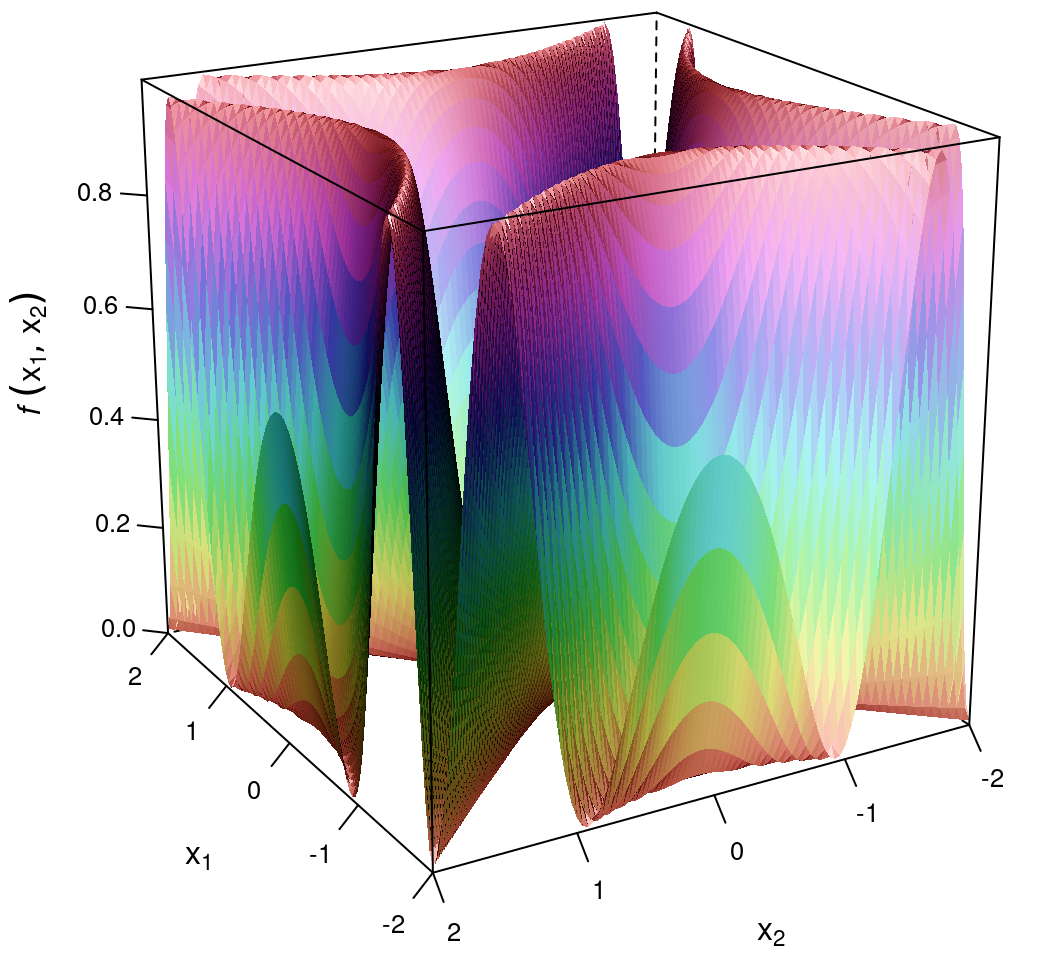
图 14.8: Schaffer 函数

14.4.2.6 Hölder 函数

Hölder 桌面函数

$f(x_1,x_2) = - | \sin(x_1)\cos(x_2)\exp\big(| 1 - \frac{\sqrt{x_1^2 + x_2^2}}{\pi}|\big) |$

在 $(8.05502, 9.66459)$ 、 $(-8.05502, 9.66459)$ 、 $(8.05502, -9.66459)$ 、 $(-8.05502, -9.66459)$ 同时取得最小值 $-19.2085$ 。

fn <- function(x) {
  -abs(sin(x[1]) * cos(x[2])) * exp(abs(1 - sqrt(x[1]^2 + x[2]^2) / pi))
}

df <- expand.grid(
  x = seq(-10, 10, length = 101),
  y = seq(-10, 10, length = 101)
)
df$fnxy = apply(df, 1, fn)

wireframe(
  data = df, fnxy ~ x * y,
  shade = TRUE, drape = FALSE,
  xlab = expression(x[1]), 
  ylab = expression(x[2]), 
  zlab = list(expression(italic(f) ~ group("(", list(x[1], x[2]), ")")), rot = 90),
  scales = list(arrows = FALSE, col = "black"),
  par.settings = list(axis.line = list(col = "transparent")),
  screen = list(z = 120, x = -60, y = 0)
)

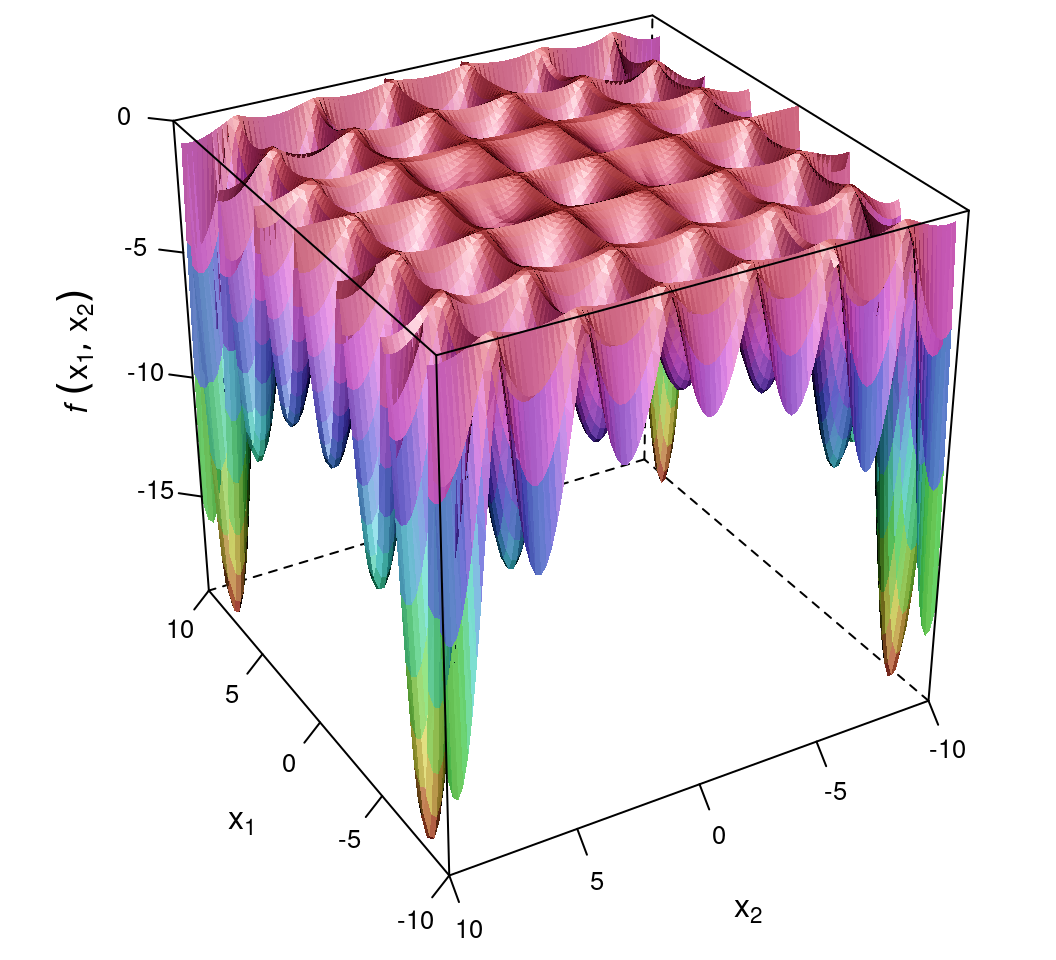
图 14.9: Hölder 函数

14.4.2.7 Trid 函数

$n \geq 2$ 维 Trid 函数

$f(x) = \sum_{i=1}^{n}(x_i - 1)^2 - \sum_{i=2}^{n}x_i x_{i-1}$ $\forall i = 1,2,\cdots, n$ ， $f(x)$ 在 $x_i = i(n+1-i)$ 处取得全局极小值 $f(\mathbf{x}^\star)=-n(n+4)(n-1)/6$ ，取值区间 $x \in [-n^2, n^2], \forall i = 1,2,\cdots,n$

fn <- function(x) {
  n <- length(x)
  sum((x - 1)^2) - sum(x[-1] * x[-n])
}

df <- expand.grid(
  x = seq(-4, 4, length = 101),
  y = seq(-4, 4, length = 101)
)
df$fnxy = apply(df, 1, fn)

wireframe(
  data = df, fnxy ~ x * y,
  shade = TRUE, drape = FALSE,
  xlab = expression(x[1]), 
  ylab = expression(x[2]), 
  zlab = list(expression(italic(f) ~ group("(", list(x[1], x[2]), ")")), rot = 90),
  scales = list(arrows = FALSE, col = "black"),
  par.settings = list(axis.line = list(col = "transparent")),
  screen = list(z = -60, x = -70, y = 0)
)

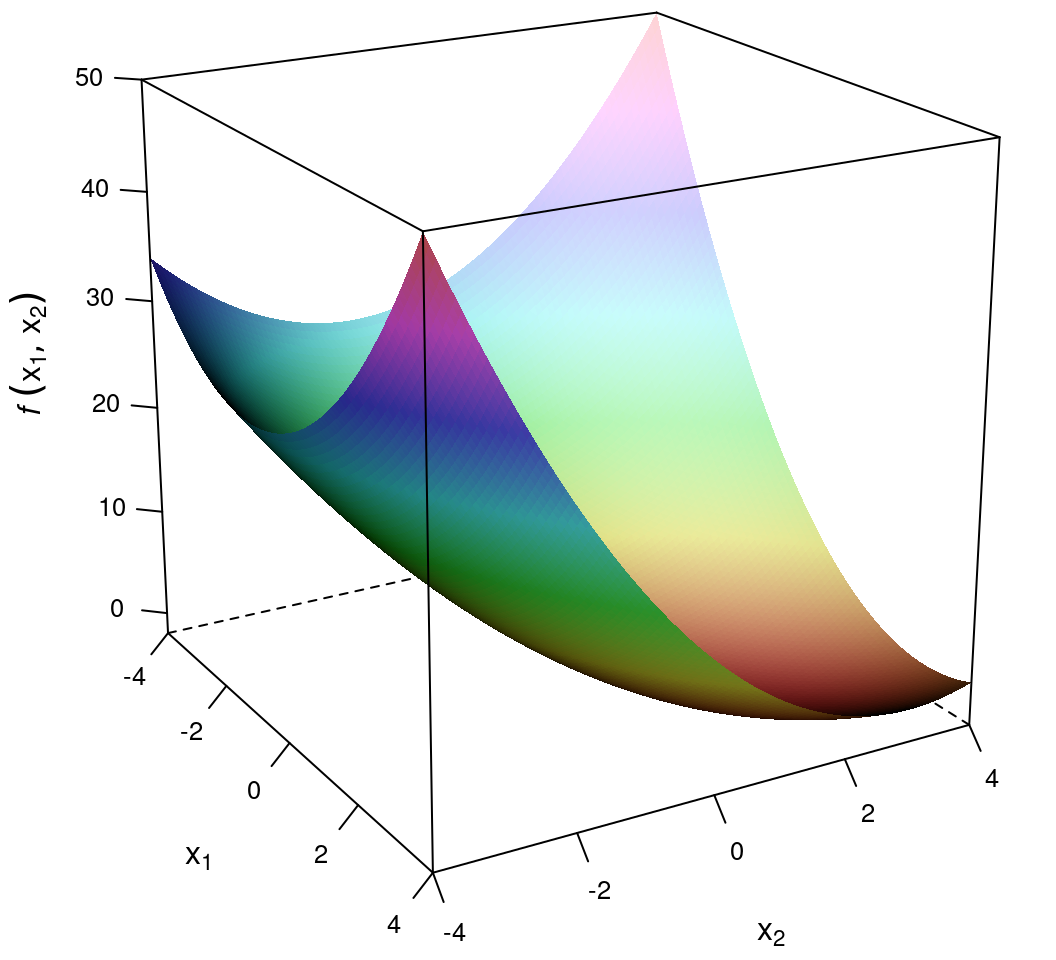
图 14.10: Trid 函数

14.4.3 多元非线性约束优化

14.4.3.1 非线性严格不等式约束

第一个例子，目标函数是非线性的，约束条件也是非线性的，非线性不等式约束不包含等号。

$\begin{equation*} \begin{array}{l} \min_x \quad (x_1 + 3x_2 + x_3)^2 + 4(x_1 - x_2)^2 \\ s.t.\left\{ \begin{array}{l} x_1 + x_2 + x_3 = 1 \\ 6 x_2 + 4 x_3 - x_1^3 > 3 \\ x_1, x_2, x_3 > 0 \end{array} \right. \end{array} \end{equation*}$

# 目标函数
fn <- function(x) (x[1] + 3 * x[2] + x[3])^2 + 4 * (x[1] - x[2])^2
# 目标函数的梯度
gr <- function(x) {
  c(
    2 * (x[1] + 3 * x[2] + x[3]) + 8 * (x[1] - x[2]), # 对 x[1] 求偏导
    6 * (x[1] + 3 * x[2] + x[3]) - 8 * (x[1] - x[2]), # 对 x[2] 求偏导
    2 * (x[1] + 3 * x[2] + x[3]) # 对 x[3] 求偏导
  )
}
# 等式约束
heq <- function(x) {
  x[1] + x[2] + x[3] - 1 
}
# 等式约束的雅可比矩阵
# 这里只有一个等式约束，所以雅可比矩阵行数为 1
heq.jac <- function(x) {
  matrix(c(1, 1, 1), ncol = 3, byrow = TRUE)
}
# 不等式约束
# 要求必须是严格不等式，不能带等号，方向是 x > 0 
hin <- function(x) {
  c(6 * x[2] + 4 * x[3] - x[1]^3 - 3, x[1], x[2], x[3])
}
# 不等式约束的雅可比矩阵
# 其实是有 4 个不等式约束，3 个目标变量约束，雅可比矩阵行数是 4
hin.jac <- function(x) {
  matrix(c(
    -3 * x[1]^2, 6, 4,
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ), ncol = 3, byrow = TRUE)
}

调用 alabama 包的求解器

set.seed(12)
# 初始值
p0 <- runif(3)
# 求目标函数的极小值
ans <- alabama::constrOptim.nl(
  par = p0,
  # 目标函数
  fn = fn,
  gr = gr,
  # 等式约束
  heq = heq,
  heq.jac = heq.jac,
  # 不等式约束
  hin = hin,
  hin.jac = hin.jac,
  # 不显示迭代过程
  control.outer = list(trace = FALSE)
)
ans

## $par
## [1] 7.390292e-04 4.497160e-12 9.992610e-01
## 
## $value
## [1] 1.000002
## 
## $counts
## function gradient 
##     1230      163 
## 
## $convergence
## [1] 0
## 
## $message
## NULL
## 
## $hessian
##           [,1]      [,2]      [,3]
## [1,] 120517098 120517087 120517091
## [2,] 120517087 120517115 120517095
## [3,] 120517091 120517095 120517091
## 
## $outer.iterations
## [1] 13
## 
## $lambda
## [1] 4.481599
## 
## $sigma
## [1] 120517089
## 
## $barrier.value
## [1] 0.003472071
## 
## $K
## [1] 4.269112e-08

ans 是 constrOptim.nl() 返回的一个 list， convergence = 0 表示迭代成功收敛，value 表示目标函数在迭代终止时的取直，par 表示满足约束条件，成功收敛的情况下，目标函数的参数值，counts 表示迭代过程中目标函数及其梯度计算的次数。

# 不提供梯度函数，照样可以求解
ans <- alabama::constrOptim.nl(par = p0, fn = fn, heq = heq, hin = hin)

等式和不等式约束的雅可比矩阵必须以 matrix 数据类型存储，而不能以 vector 类型存储。要注意和后面 ROI 包的调用形式区别。

实际上，可以用 ROI 调用 alabama 求解器的方式，这种方式可以简化目标函数梯度和约束条件的表示

# 目标函数
fn <- function(x) (x[1] + 3 * x[2] + x[3])^2 + 4 * (x[1] - x[2])^2
# 目标函数的梯度
gr <- function(x) {
  c(
    2 * (x[1] + 3 * x[2] + x[3]) + 8 * (x[1] - x[2]),
    6 * (x[1] + 3 * x[2] + x[3]) - 8 * (x[1] - x[2]),
    2 * (x[1] + 3 * x[2] + x[3])
  )
}
heq <- function(x) {
  x[1] + x[2] + x[3]
}
heq.jac <- function(x) {
  c(1, 1, 1)
}
hin <- function(x) {
  6 * x[2] + 4 * x[3] - x[1]^3
}
hin.jac <- function(x) {
   c(-3 * x[1]^2, 6, 4)
}

通过 ROI 调用 alabama 求解器

set.seed(2020)
# 初始值
p0 <- runif(3)
# 定义目标规划
op <- OP(
  objective = F_objective(F = fn, n = 3L, G = gr), # 4 个目标变量
  constraints = F_constraint(
    F = list(heq = heq, hin = hin),
    dir = c("==", ">"),
    rhs = c(1, 3),
    # 等式和不等式约束的雅可比
    J = list(heq.jac = heq.jac, hin.jac = hin.jac)
  ),
  bounds = V_bound(ld = 0, ud = +Inf, nobj = 3L),
  maximum = FALSE # 求最小
)
nlp <- ROI_solve(op, solver = "alabama", start = p0)
nlp$solution

## [1] 1.674812e-06 9.994336e-08 9.999982e-01

nlp$objval

## [1] 1

14.4.3.2 非线性混合整数约束

$\begin{equation*} \begin{array}{l} \max_x \quad 1.5(x_1 - \sin(x_1 - x_2))^2 + 0.5x_2^2 + x_3^2 - x_1 x_2 - 2x_1 + x_2 x_3 \\ s.t.\left\{ \begin{array}{l} -20 < x_1 < 20 \\ -20 < x_2 < 20 \\ -10 < x_3 < 10 \\ x_1, x_2 \in \mathbb{R}, \quad x_3 \in \mathbb{Z} \end{array} \right. \end{array} \end{equation*}$

fn <- function(x) {
  1.5 * (x[1] - sin(x[1] - x[2]))^2 + 0.5 * x[2]^2 + x[3]^2
  -x[1] * x[2] - 2 * x[1] + x[2] * x[3]
}
gr <- function(x) {
  c(
    3 * (x[1] - sin(x[1] - x[2])) * (1 - cos(x[1] - x[2])) - x[2] - 2,
    3 * (x[1] - sin(x[1] - x[2])) * cos(x[1] - x[2]) - x[2] - x[1] + x[3],
    2 * x[3] + x[2]
  )
}

目前 ROI 还解不了

# 初始值
p0 <- c(2.1, 5.1, 5)
# 定义目标规划
op <- OP(
  objective = F_objective(F = fn, n = 3L, G = gr), # 3 个目标变量
  types = c("C", "C", "I"), # 目标变量的类型
  bounds = V_bound(lb = c(-20, -20, -10), ub = c(20, 20, 10), nobj = 3L),
  maximum = FALSE # 求最小
)
nlp <- ROI_solve(op, solver = "auto", start = p0)
nlp$solution

目标函数在 $(4.49712, 9.147501, -4)$ 取得最小值 -86.72165

fn(x = c(4.49712, 9.147501, -4))

## [1] -86.72165

14.4.3.3 含复杂目标函数

下面这个目标函数比较复杂，约束条件也是非线性的

$\begin{equation*} \begin{array}{l} \max_x \quad \frac{(\sin(2\pi x_1))^3 \sin(2\pi x_2)}{x_1^3 (x_1 + x_2)} \\ s.t.\left\{ \begin{array}{l} x_1^2 - x_2 + 1 \leq 0 \\ 1 - x_1 + (x_2 - 4)^2 \geq 0 \\ 0 \leq x_1, x_2 \leq 10 \end{array} \right. \end{array} \end{equation*}$

# 目标函数
fn <- function(x) (sin(2*pi*x[1]))^3 * sin(2*pi*x[2])/(x[1]^3*(x[1] + x[2]))
# 目标函数的梯度
gr <- function(x) {
  numDeriv::grad(fn, c(x[1], x[2]))
}

hin <- function(x) {
  c(
    x[1]^2 - x[2] + 1,
    1 - x[1] + (x[2] - 4)^2
  )
}

hin.jac <- function(x) {
  matrix(c(
    2 * x[1], -1,
    -1, 2 * x[2]
  ),
  ncol = 2, byrow = TRUE
  )
}

# 初始值
p0 <- c(2, 5)
# 定义目标规划
op <- OP(
  objective = F_objective(F = fn, n = 2L, G = gr), # 2 个目标变量
  constraints = F_constraint(
    F = list(hin = hin),
    dir = c("<=", "<="),
    rhs = c(0, 0),
    # 不等式约束的雅可比
    J = list(hin.jac = hin.jac)
  ),
  bounds = V_bound(ld = 0, ud = 10, nobj = 2L),
  maximum = TRUE # 求最大
)
nlp <- ROI_solve(op, solver = "nloptr.isres", start = p0)
nlp$solution

## [1] 1.227969 4.245379

nlp$objval

## [1] 0.09582504