Practical 4 Solutions
Try to at least finish Questions 1 and 2 from Practical 3 before continuing with this practical! It might be tempting to skip some stuff if you’re behind, but you may end up more lost\(...\)we will happily answer questions from any previous practical each session.
In this practical, we will start by considering the seatpos dataset in library faraway.
Q1 Data Analysis
This question focuses on generally improving your data analytical skills, so just go with it! A subsequent lasso regression analysis follows in Question 2.
- Load library
farawayand check the help file for datasetseatpos.
library(faraway)
?seatpos- Looking at the help file, which variable might the researchers at the HuMoSim laboratory consider to be a good response variable?
# hipcenter would be a good response variable, as it is the only variable
# in the dataset that considers the location of a person within the car.
# This can be used as a proxy for where different drivers will position the
# seat, which is the quantity of interest for car designers.- Using the help file only for the moment (that is, without performing any analysis on the dataset), are there any predictor variables that we think may be likely to be highly correlated?
# Many of the predictors could be highly correlated.
# Examples include:
# - height and weight (a whole analysis could be done on this
# pairing),
# - lower leg length and thigh length - I would suspect people with
# longer lower legs also have longer thighs, but maybe I'm wrong.
# - Ht and HtShoes - these two variables measure height bare foot and in
# shoes - given that people's heights are in general not going to increase
# much by putting on a pair of shoes (and possibly by roughly a similar
# amount for each person), these variables are likely to be (very) highly
# correlated. I would question including both of these variables
# in an analysis, although our computational analyses will confirm whether
# this is the case.
#
# Perhaps Age is unlikely to be too highly correlated with any of the other
# variables.
# Note that the aim of this question is to get you to think about the
# dataset before we go headlong into applying computational methods, since
# this is what a statistician/data scientist/machine learner should do!- What is the dimension of the dataset? Check whether there is any missing data.
dim( seatpos ) # 38 samples, 9 variables.## [1] 38 9sum(is.na(seatpos)) # no missing data.## [1] 0- Use exploratory data analysis commands and plots to investigate the correlation of
hipcenterwith the other (possible predictor) variables. With which predictor variables ishipcentermost correlated? Are those predictor variables correlated with each other? Does this exploratory analysis support your initial thoughts from part (c)? What do your findings here suggest about the fixed location referred to in the help file for description ofhipcenter(is it in front or behind the driver)?
# We can calculate the correlation of `hipcenter` to the other variables.
# Note that the response is the ninth variable in this dataset.
cor(seatpos[,9], seatpos[,-9]) ## Age Weight HtShoes Ht Seated Arm Thigh
## [1,] 0.2051722 -0.640333 -0.7965964 -0.7989274 -0.7312537 -0.585095 -0.5912015
## Leg
## [1,] -0.7871685# From this we see that `hipcenter` has a reasonable negative correlation
# with most of the predictors, apart from age.
# We display the correlation matrix across the eight predictors as follows.
cor( seatpos[,-9] )## Age Weight HtShoes Ht Seated Arm Thigh
## Age 1.00000000 0.08068523 -0.07929694 -0.09012812 -0.1702040 0.3595111 0.09128584
## Weight 0.08068523 1.00000000 0.82817733 0.82852568 0.7756271 0.6975524 0.57261442
## HtShoes -0.07929694 0.82817733 1.00000000 0.99814750 0.9296751 0.7519530 0.72486225
## Ht -0.09012812 0.82852568 0.99814750 1.00000000 0.9282281 0.7521416 0.73496041
## Seated -0.17020403 0.77562705 0.92967507 0.92822805 1.0000000 0.6251964 0.60709067
## Arm 0.35951115 0.69755240 0.75195305 0.75214156 0.6251964 1.0000000 0.67109849
## Thigh 0.09128584 0.57261442 0.72486225 0.73496041 0.6070907 0.6710985 1.00000000
## Leg -0.04233121 0.78425706 0.90843341 0.90975238 0.8119143 0.7538140 0.64954120
## Leg
## Age -0.04233121
## Weight 0.78425706
## HtShoes 0.90843341
## Ht 0.90975238
## Seated 0.81191429
## Arm 0.75381405
## Thigh 0.64954120
## Leg 1.00000000# Many of the predictors are reasonably highly correlated with each other,
# except for Age.
# As suspected the pairing with greatest correlation is Ht and HtShoes.
# We could obtain a pairs plot across the dataset.
pairs( seatpos, pch = 16, col = 2 )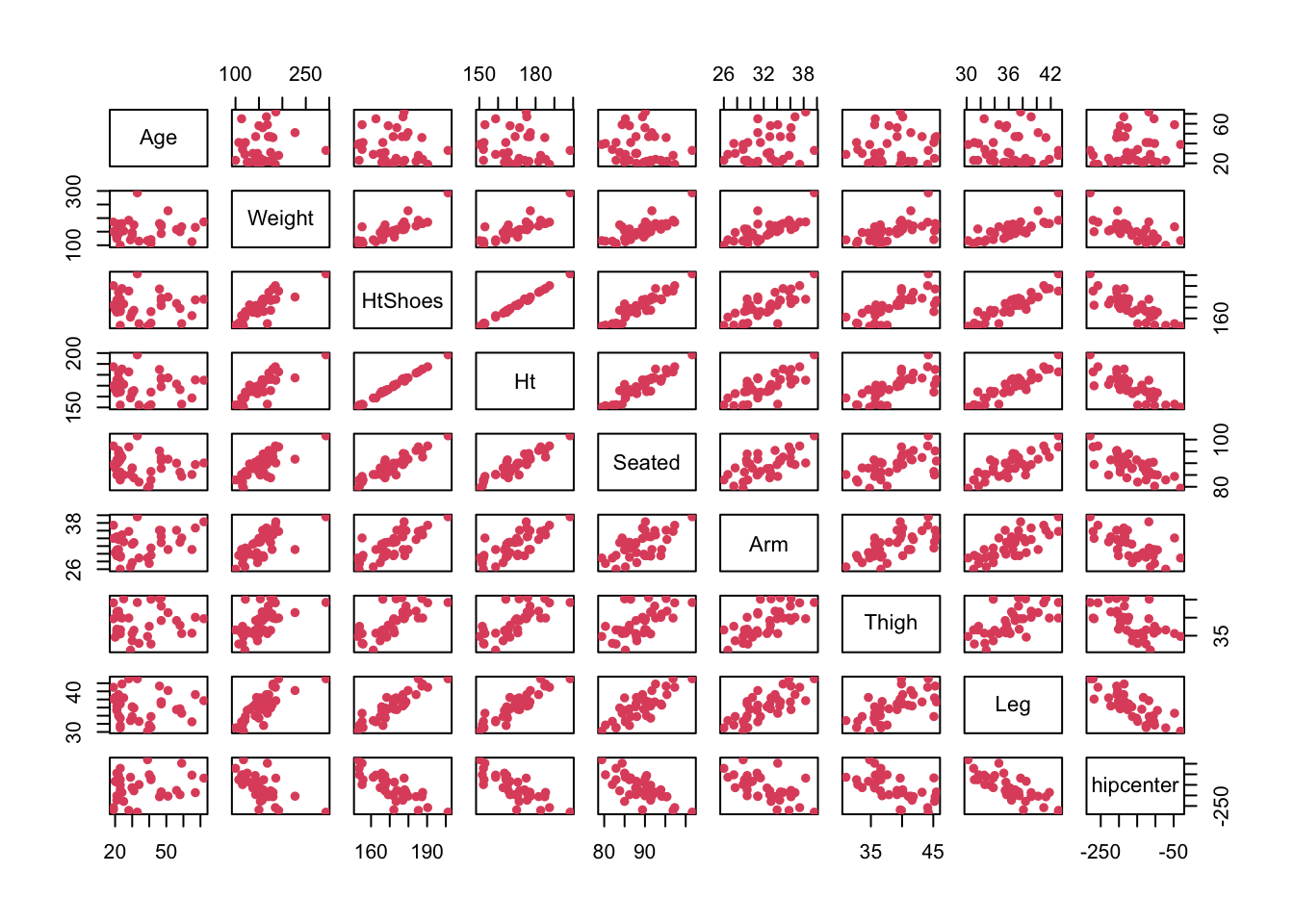
# These support the comments and correlations seen above.
# I would hazard a guess that the fixed location in the car is behind the
# driver, since the distance from it to the drivers hips gets smaller as
# the driver's various dimensions (in general) get larger. Larger drivers
# are likely to move their seat back, so to make the distance shorter, the
# fixed position should be behind the driver.
# Note: these are my interpretations of the dataset, but again the purpose
# of this question is about getting you to think logically about the data
# you have been presented with.
# This can sometimes be harder than the computational side of things.
# In particular it may help to catch any coding errors (and potential
# illogical reasonings and conclusions) later! Q2 Lasso Regression
Load library glmnet. Fit a model of all of the remaining variables for hipcenter using lasso regression. Plot regularisation paths against log \(\lambda\) and \(\ell_1\) norm values. Investigate which variables are included under various values of \(\lambda\). Do you notice anything interesting about the trends for the predictors Ht and HtShoes? Do the findings here support exploratory analysis of Question 1?
library("glmnet")
y = seatpos$hipcenter
x = model.matrix(hipcenter~., seatpos)[,-1]
lasso = glmnet(x, y)
par(mfrow = c(1,2))
plot(lasso, xvar = 'lambda')
plot(lasso)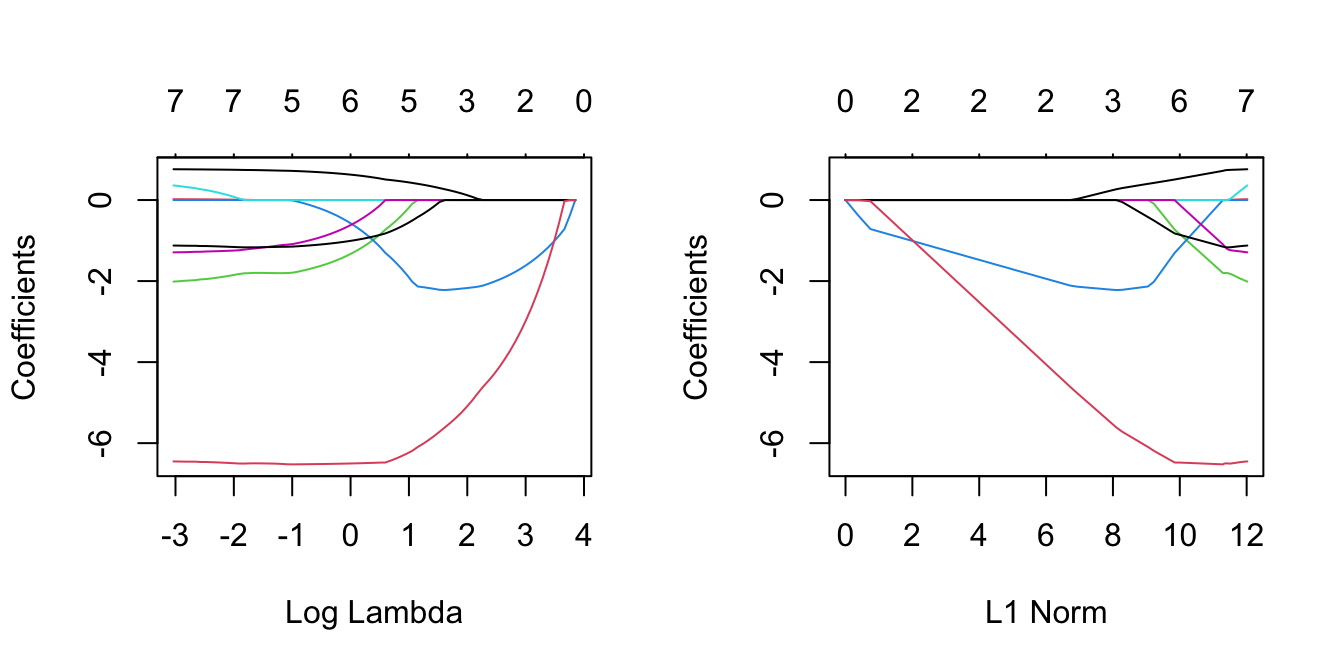
# We can see which values of lambda were in the grid.
lasso$lambda## [1] 47.02272566 42.84535631 39.03909294 35.57096752 32.41094081 29.53164215 26.90813246
## [8] 24.51768813 22.33960429 20.35501542 18.54673195 16.89909140 15.39782269 14.02992256
## [15] 12.78354291 11.64788819 10.61312191 9.67028141 8.81120026 8.02843751 7.31521325
## [22] 6.66534987 6.07321856 5.53369056 5.04209274 4.59416712 4.18603397 3.81415825
## [29] 3.47531895 3.16658119 2.88527084 2.62895133 2.39540254 2.18260158 1.98870527
## [36] 1.81203418 1.65105806 1.50438261 1.37073740 1.24896487 1.13801027 1.03691258
## [43] 0.94479612 0.86086304 0.78438634 0.71470362 0.65121132 0.59335950 0.54064708
## [50] 0.49261748 0.44885470 0.40897969 0.37264706 0.33954212 0.30937814 0.28189383
## [57] 0.25685116 0.23403321 0.21324235 0.19429849 0.17703754 0.16131002 0.14697968
## [64] 0.13392241 0.12202511 0.11118474 0.10130739 0.09230752 0.08410718 0.07663533
## [71] 0.06982726 0.06362399 0.05797181 0.05282176 0.04812922# We can see which variables were included under each of those.
lasso$beta## 8 x 75 sparse Matrix of class "dgCMatrix"## [[ suppressing 75 column names 's0', 's1', 's2' ... ]]##
## Age . . . . . . . .
## Weight . . . . . . . .
## HtShoes . . . . . . . .
## Ht . -0.3788888 -0.71690000 -0.8815363 -1.031066 -1.168389 -1.292464 -1.406576
## Seated . . . . . . . .
## Arm . . . . . . . .
## Thigh . . . . . . . .
## Leg . . -0.03001398 -0.5709448 -1.065255 -1.512438 -1.923026 -2.293971
##
## Age . . . . . . . .
## Weight . . . . . . . .
## HtShoes . . . . . . . .
## Ht -1.509502 -1.604347 -1.689716 -1.768569 -1.839363 -1.904943 -1.963641 -2.017036
## Seated . . . . . . . .
## Arm . . . . . . . .
## Thigh . . . . . . . .
## Leg -2.635099 -2.942743 -3.226199 -3.481281 -3.716848 -3.928280 -4.124080 -4.302752
##
## Age . . 0.03026313 0.07914329 0.123651 0.164252 0.2011991
## Weight . . . . . . .
## HtShoes . . . . . . .
## Ht -2.066746 -2.111083 -2.13956040 -2.15657249 -2.172738 -2.186422 -2.1999306
## Seated . . . . . . .
## Arm . . . . . . .
## Thigh . . . . . . .
## Leg -4.462389 -4.610703 -4.77565830 -4.94857151 -5.104146 -5.249008 -5.3779072
##
## Age 0.2349099 0.2656318 0.29557296 0.3254539 0.3526374 0.3774918 0.4000568
## Weight . . . . . . .
## HtShoes . . . . . . .
## Ht -2.2112247 -2.2213847 -2.21537008 -2.1919535 -2.1710512 -2.1509204 -2.1336034
## Seated . . . . . . .
## Arm . . . . . . .
## Thigh . . -0.04904616 -0.1550600 -0.2512560 -0.3396447 -0.4194801
## Leg -5.4983751 -5.6085302 -5.71786751 -5.8252121 -5.9220281 -6.0129224 -6.0932133
##
## Age 0.42215302 0.4425705 0.4611742 0.4781344 0.4935876 0.507660431 0.5325412
## Weight . . . . . . .
## HtShoes -0.08747275 -0.2410930 -0.3810765 -0.5094711 -0.6264423 -0.732315652 -0.8541160
## Ht -2.02086133 -1.8495163 -1.6933835 -1.5502583 -1.4198654 -1.301776165 -1.1523513
## Seated . . . . . . .
## Arm . . . . . -0.003724438 -0.1356874
## Thigh -0.50353183 -0.5808560 -0.6513109 -0.7155662 -0.7741120 -0.825232452 -0.8617522
## Leg -6.18702261 -6.2568841 -6.3205372 -6.3785468 -6.4314027 -6.478380251 -6.4798559
##
## Age 0.5538978 0.5733715 0.5910974 0.6072458 0.6219709 0.6353911 0.6476155
## Weight . . . . . . .
## HtShoes -0.9612630 -1.0599721 -1.1485746 -1.2290941 -1.3032866 -1.3710911 -1.4325446
## Ht -1.0218632 -0.9018626 -0.7938899 -0.6957256 -0.6054368 -0.5229599 -0.4481416
## Seated . . . . . . .
## Arm -0.2445963 -0.3438619 -0.4342699 -0.5166409 -0.5917202 -0.6601388 -0.7224752
## Thigh -0.8945363 -0.9244800 -0.9516743 -0.9764387 -0.9990584 -1.0196829 -1.0384553
## Leg -6.4847698 -6.4892510 -6.4933288 -6.4970433 -6.5004312 -6.5035202 -6.5063374
##
## Age 0.6587657 0.6689108 0.6781749 0.6865932 0.6942714 0.7012737 0.70765527
## Weight . . . . . . .
## HtShoes -1.4893806 -1.5398858 -1.5875253 -1.6288279 -1.6673273 -1.7029099 -1.73553063
## Ht -0.3791066 -0.3175022 -0.2597176 -0.2091840 -0.1622689 -0.1190003 -0.07936592
## Seated . . . . . . .
## Arm -0.7793014 -0.8310560 -0.8782503 -0.9212114 -0.9603579 -0.9960311 -1.02852223
## Thigh -1.0556179 -1.0711783 -1.0854622 -1.0983601 -1.1101614 -1.1209538 -1.13080691
## Leg -6.5089124 -6.5112740 -6.5134288 -6.5154515 -6.5172794 -6.5189702 -6.52053931
##
## Age 0.71346592 0.7187507 0.7228005 0.7250685 0.7283275 0.731506 0.734511
## Weight . . . . . . .
## HtShoes -1.76517488 -1.7918480 -1.8012793 -1.8042393 -1.8036976 -1.802075 -1.800008
## Ht -0.04332879 -0.0108381 . . . . .
## Seated . . . . . . .
## Arm -1.05809285 -1.0849764 -1.1006536 -1.1107097 -1.1284351 -1.145882 -1.162368
## Thigh -1.13978543 -1.1479486 -1.1525898 -1.1535925 -1.1565048 -1.159510 -1.162575
## Leg -6.52200063 -6.5233662 -6.5216161 -6.5131065 -6.5068898 -6.503318 -6.501111
##
## Age 0.737307 0.739810222 0.741186412 0.742529970 0.745354326 0.74742495
## Weight . 0.001075362 0.003693442 0.006652873 0.008513292 0.01013531
## HtShoes -1.797816 -1.798603166 -1.803557433 -1.808553585 -1.827269779 -1.85186185
## Ht . . . . . .
## Seated . . . 0.002378954 0.040515474 0.08294766
## Arm -1.177701 -1.194759877 -1.207604764 -1.224531973 -1.239936898 -1.24773622
## Thigh -1.165548 -1.166929365 -1.167273424 -1.167232842 -1.163875042 -1.15825820
## Leg -6.499640 -6.497567833 -6.499442317 -6.503591032 -6.502812684 -6.49475353
##
## Age 0.7490595 0.75051743 0.75188196 0.75309161 0.75422793 0.75592912
## Weight 0.0117728 0.01326849 0.01463865 0.01587222 0.01700937 0.01736582
## HtShoes -1.8757287 -1.89667200 -1.91673747 -1.93407617 -1.95075883 -1.95798264
## Ht . . . . . .
## Seated 0.1225952 0.15754489 0.19096305 0.21992109 0.24771599 0.26649454
## Arm -1.2530833 -1.25803785 -1.26232015 -1.26641490 -1.26997742 -1.27709493
## Thigh -1.1526247 -1.14780561 -1.14306697 -1.13909162 -1.13514900 -1.13506802
## Leg -6.4872853 -6.48122990 -6.47512351 -6.47010118 -6.46501672 -6.46519803
##
## Age 0.75628200 0.75774078 0.75870481 0.75951416 0.76009998
## Weight 0.01888635 0.01919551 0.01980897 0.02057163 0.02118573
## HtShoes -1.97774056 -1.98463485 -1.99295752 -2.00426952 -2.01275176
## Ht . . . . .
## Seated 0.29335360 0.31078418 0.32692789 0.34634309 0.36049535
## Arm -1.27745387 -1.28286904 -1.28666067 -1.28881721 -1.29085662
## Thigh -1.12899125 -1.12874195 -1.12739244 -1.12473708 -1.12283674
## Leg -6.45672861 -6.45697888 -6.45593029 -6.45313255 -6.45077390# In particular, high values of lambda leads to inclusion of Ht only.
# Other variables start to come in; leg, followed by Age,
# followed by Thigh, as lambda gets smaller.
# It is interesting that Age comes in third, despite having a reasonably
# small correlation with the response.
# However, this may be as expected, since the other variables also have
# high correlations with each other (collinearity), whereas Age may
# contain alternative predictive information.
# Interestingly, HtShoes enters only for small enough values of lambda, at
# which point its coefficients increase whilst the Ht coefficients
# decrease, eventually to zero.
# This is to do with the ridiculously high correlation between Ht
# and HtShoes (spotted in Q1) - even for really low values of lambda,
# we don't need both of these variables.Q3 Principal Component Regression
- Load library
pls(required for PCR).
library("pls")- Use the command
pcrto fit a principal component regression model tohipcenterbased on the remaining variables. Select the number of principal components using cross-validation. Remember to standardise the variables. How many principal components are recommended, according to the cross-validation error?
pcr.fit=pcr(hipcenter~., data=seatpos, scale = TRUE, validation = "CV" )
summary(pcr.fit)## Data: X dimension: 38 8
## Y dimension: 38 1
## Fit method: svdpc
## Number of components considered: 8
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
## CV 60.45 38.21 36.74 37.84 37.57 38.69 39.77 43.3
## adjCV 60.45 38.09 36.60 37.65 37.33 38.42 39.41 42.7
## 8 comps
## CV 43.69
## adjCV 43.07
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps
## X 70.91 86.37 92.17 95.18 97.61 99.35 99.98 100.00
## hipcenter 61.89 66.34 66.48 67.82 68.02 68.58 68.63 68.66# The summary suggests use of 2 principal components.- Approriately plot the mean squared validation error.
validationplot( pcr.fit, val.type = 'MSEP' )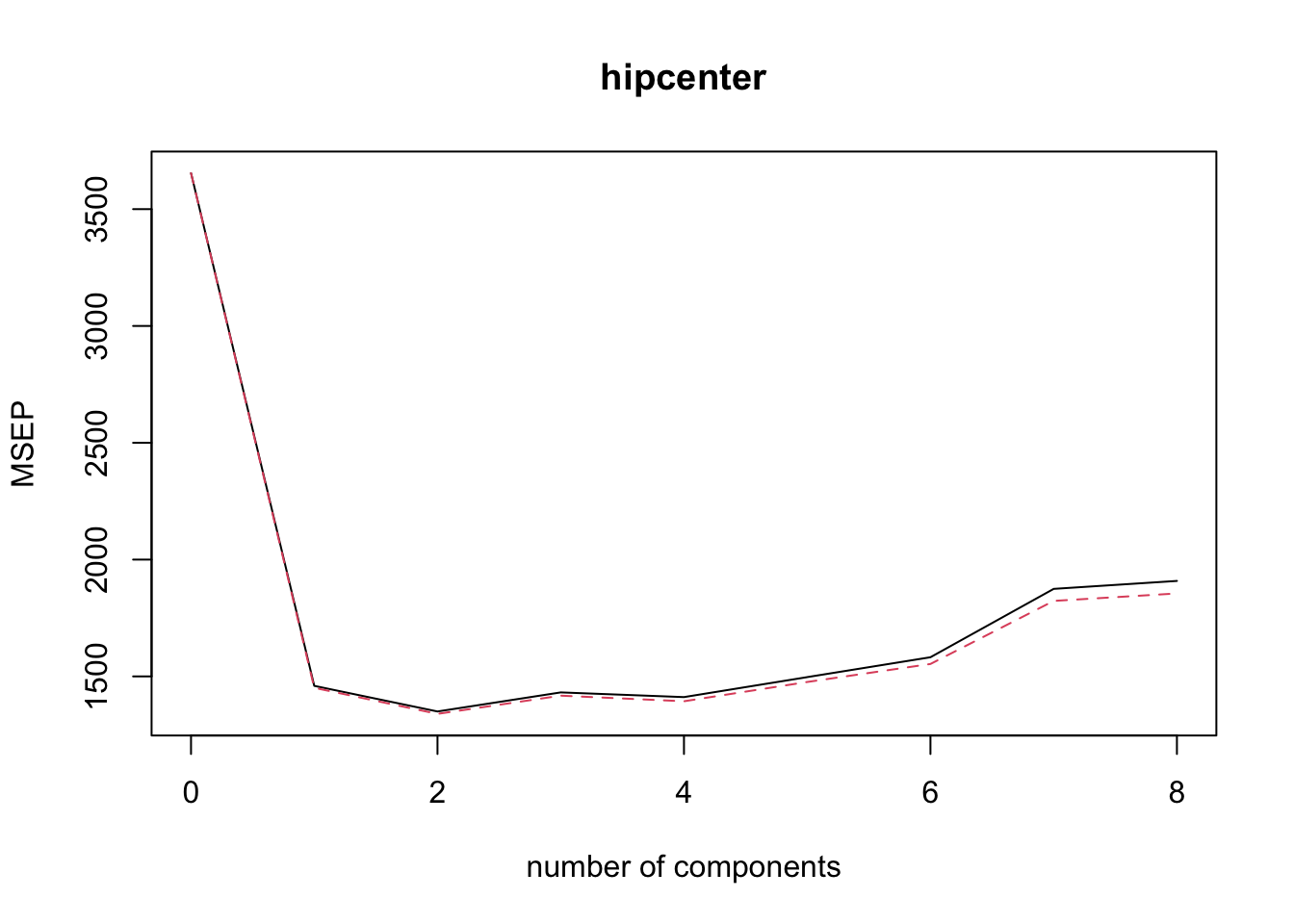
- Use the command
coef()to find corresponding coefficient estimates in terms of the original \(\hat{\beta}\)’s. How do these estimates coincide with the exploratory analysis of Question 1?
coef(pcr.fit, ncomp = 2)## , , 2 comps
##
## hipcenter
## Age 9.779064
## Weight -6.721580
## HtShoes -9.301406
## Ht -9.385585
## Seated -9.978190
## Arm -2.633940
## Thigh -5.035274
## Leg -8.307696# Since Age had a positive correlation with hipcenter, the coefficient
# is positive. For the remaining variables the correlation was negative,
# so the coefficients are negative.
# Notice how the size of the coefficients is relatively similar across
# all predictor variables.
# This is to do with how Principal Component Analysis works.Q4 Predictive Accuracy of Methods
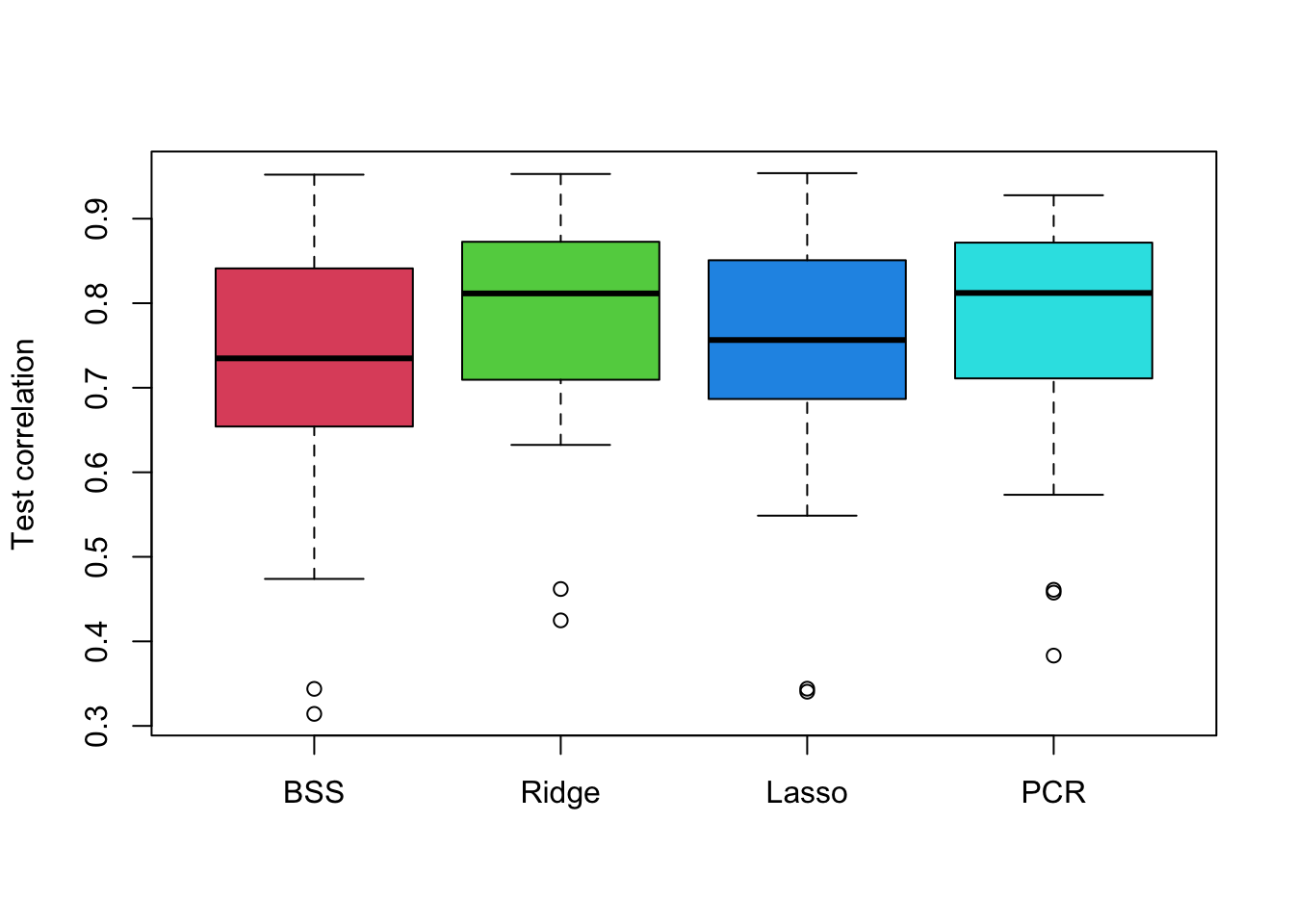
Use 50 repetitions of data-splitting with 28 samples for training (10 for testing) to compare the predictive performance of the following models of the remaining predictors for hipcenter:
- Best subset selection with \(C_p\)
- Ridge with min-CV \(\lambda\) (5 folds)
- Lasso with min-CV \(\lambda\) (5 folds)
- PCR with min-CV number of principal components.
# Load R libraries.
library(leaps)
# Predict function for regsubsets
predict.regsubsets = function(object, newdata, id, ...){
form = as.formula(object$call[[2]])
mat = model.matrix(form, newdata)
coefi = coef(object, id = id)
xvars = names(coefi)
mat[, xvars]%*%coefi
}
repetitions = 50
cor.bss = c()
cor.ridge = c()
cor.lasso = c()
cor.pcr = c()
set.seed(1)
for(i in 1:repetitions){
# Step (i) data splitting
training.obs = sample(1:38, 28)
y.train = seatpos$hipcenter[training.obs]
x.train = model.matrix(hipcenter~., seatpos[training.obs, ])[,-1]
y.test = seatpos$hipcenter[-training.obs]
x.test = model.matrix(hipcenter~., seatpos[-training.obs, ])[,-1]
# Step (ii) training phase
bss.train = regsubsets(hipcenter~., data=seatpos[training.obs,], nvmax=8)
min.cp = which.min(summary(bss.train)$cp)
ridge.train = cv.glmnet(x.train, y.train, alpha = 0, nfolds = 5)
lasso.train = cv.glmnet(x.train, y.train, nfold = 5)
pcr.train = pcr(hipcenter~., data =seatpos[training.obs,],
scale = TRUE, validation="CV")
min.pcr = which.min(MSEP(pcr.train)$val[1,1, ] ) - 1
# Step (iii) generating predictions
predict.bss = predict.regsubsets(bss.train, seatpos[-training.obs, ], min.cp)
predict.ridge = predict(ridge.train, x.test, s = 'lambda.min')
predict.lasso = predict(lasso.train, x.test, s = 'lambda.min')
predict.pcr = predict(pcr.train,seatpos[-training.obs, ], ncomp = min.pcr )
# Step (iv) evaluating predictive performance
cor.bss[i] = cor(y.test, predict.bss)
cor.ridge[i] = cor(y.test, predict.ridge)
cor.lasso[i] = cor(y.test, predict.lasso)
cor.pcr[i] = cor(y.test, predict.pcr)
}
# Plot the resulting correlations as boxplots.
boxplot(cor.bss, cor.ridge, cor.lasso, cor.pcr,
names = c('BSS','Ridge', 'Lasso', 'PCR'),
ylab = 'Test correlation', col = 2:5)