3.2 Random Number Generation

Sheldon: I’ll create an algorithm that will generate a pseudorandom schedule. Do you know why it will not be a “true” random schedule?

Amy: Because the generation of true random numbers remains an unsolved problem in computer science?

- Big Bang Theory, Season 12, Episode 1

Many of the methods in computational statistics require the ability to generate random variables from known probability distributions.

Random numbers have been used for thousands of years in decision-making, divination, and games. Ancient civilizations cast lots, rolled dice, and drew straws; Babylonians held lotteries, while Greeks and Romans used dice for leisure and governance.

With the rise of gambling in the 17th and 18th centuries, randomness gained prominence in games of chance, coinciding with the development of probability theory by mathematicians like Pascal and Fermat.

But gambling aside, randomness has many uses in science, statistics, cryptography and more.

The use of random numbers in statistics has expanded beyond random sampling or random assignment of treatments to experimental units. More common uses now are in simulation studies of stochastic processes, analytically intractable mathematical expressions, or a population by resampling from a given sample from that population.

In this section, we explore how to generate random numbers using computers.

3.2.1 How do computers do it?

Using dice, coins, or similar media as a random device has its limitations.

Thanks to human ingenuity—and computers—we have more powerful tools and methods at our disposal.

The 20th century saw the shift from mechanical methods to electronic ones, with early computers generating random numbers for scientific applications such as the Manhattan Project.

Random numbers play a crucial role in computing, simulations, cryptography, and statistical sampling. However, not all random numbers are created in the same way.

Let’s consider first the two principal methods used to generate random numbers: true random numbers and pseudorandom numbers.

True Random Numbers

Definition 3.6 True Random Numbers are based on a physical process, and harvests the source of randomness from some physical phenomenon that is expected to be random.

Such a phenomenon takes place outside of the computer. It is measured and adjusted for possible biases due to the measurement process.

Examples include the following.

Radiation decay: The decay of unstable atomic nuclei is fundamentally unpredictable. This is detected by a Geiger counter (an electronic instrument used for detecting and measuring ionising radiation) attached to a computer.
Photon Measurements: Photons travelling through a semi-transparent mirror (or a beam splitter). The mutually exclusive events (reflection/transmission) are detected and associated to ‘0’ or ‘1’ bit values respectively.
Thermal noise: Random fluctuations in electrical circuits due to temperature variations. Thermal noise from a resistor are amplified to provide a random voltage source.

Thus, random numbers generated based on such randomness are said to be “true” random numbers.

Pseudorandom Numbers

As an alternative to “true” random numbers, the second method of generating random numbers involves computational algorithms that can produce apparently random results.

Why apparently random? Because the end results obtained are in fact completely determined by an initial value also known as the seed value or key. Therefore, if you knew the key value and how the algorithm works, you could reproduce these seemingly random results.

Definition 3.7 Pseudorandom numbers (PRNs) are generated by deterministic algorithms that produce sequences of numbers that appear random but are fully determined by an initial value, known as a seed.

Even though this type of generator typically doesn’t gather any data from sources of naturally occurring randomness, such gathering of keys can be made random when needed.

This is ideal for simulations that you want to be replicated.

Let’s compare some aspects of true random number generators or TRNGs and pseudorandom number generators or PRNGs.

Feature	True Random Numbers	Pseudorandom Numbers
Source	Physical Process	Algorithmic Computation
Reproducability	No	Yes (with seed)
Speed	Slower	Faster
Security	High	Lower
Usage	Cryptography, security	Simulations, Modelling

PRNGs are faster than TRNGs. Because of their deterministic nature, they are useful when you need to replay a sequence of random events. This helps a great deal in code testing, for example. On the other hand, TRNGs are not periodic and work better in security sensitive roles such as encryption. A period is the number of iterations a PRNG goes through before it starts repeating itself. Thus, all other things being equal, a PRNG with a longer period would take more computer resources to predict and crack.

In most statistical and computational contexts, pseudorandom numbers are sufficient, but for security-sensitive applications, true randomness is preferred.

3.2.2 General techniques for Generating Random Variables

In this section, we will demonstrate 3 methods of generating pseudorandom numbers in computers.

Linear Congruential Generator
Uniform Random Number Generator
Inverse Transform Method

The Linear Congruential Generator

Preliminaries: The modulo operator

The modulo operator finds the remainder when one number is divided by another. Mathematically, for integers $a$ and $m$ :

$a \mod m \quad =\quad \text{remainder of } \frac{a}{m}$ Properties of the Modulo Operator

Modulo Bounds

The result of $a \mod m$ is always between $0$ and $m-1$

$0 \leq (a \mod m) < m$

In the following demonstration, we will see that the value of $a \mod 3$ will just be from $0$ to $2$ .
```
a <- -5:5
a %% 3
```
```
##  [1] 1 2 0 1 2 0 1 2 0 1 2
```
Periodicity

Any integer shifted by multiples of $m$ has the same remainder.

$(a + km) \mod m \quad =\quad a \mod m$
```
1 %% 3
7 %% 3
```
```
## [1] 1
## [1] 1
```
A more general demonstration, let $a =7$ and $m = 3$ :
```
a <- 7
m <- 3

a %% m
```
```
## [1] 1
```
Now, showing for different values of $k$ , we expect that $7 + k*3 = 1$ :
```
k <- 1:5
(a + k*m) %% m
```
```
## [1] 1 1 1 1 1
```

Now, using this concept, we create an algorithm that generates a series of pseudorandom numbers.

Definition 3.8 (Linear Congruential Generator) Given an initial seed $X_0$ and integer parameters $a$ as the multiplier, $b$ as the increment, and $m$ as the modulus, the generator is defined by the linear relation:

$X_n =(aX_{n-1}+b) \quad \text{mod} \quad m$

The output is is sequence $\{X_n\}$ containing pseudorandom numbers.

Each of these members have to satisfy the following conditions:

$m > 0$ (the modulus is positive)
$0 < a < m$ (the multiplier $a$ is positive but less than the modulus $m$ ).
$0 \leq b < m$ (the increment $b$ is nonnegative but less than the modulus), and
$0 \leq X_0 < m$ (the seed $X_0$ is nonnegative but less than the modulus).

Let’s create an R function that takes the initial values as arguments and returns an array of random numbers of a given length.

lcg <- function(seed, a, b, m, n) {
    # Pre-allocate vector for efficiency
    numbers <- numeric(n)  
    x <- seed
    for (i in 1:n) {
        x <- (a * x + b) %% m
        numbers[i] <- x
    }
    return(numbers)
}

# Example: Parameters from Numerical Recipes (a common choice)
seed <- 12345
a <- 1664525
b <- 1013904223
m <- 2^32
n <- 10

lcg(seed, a, b, m, n)

##  [1]   87628868   71072467 2332836374 2726892157 3908547000  483019191
##  [7] 2129828778 2355140353 2560230508 3364893915

Key considerations:

The modulus m is often a very large prime number or power of 2 (e.g. $2^{31}-1$ or $2^{32}$ ).
The multiplier a affects the change in output for a unit increase in seed number.
The increment b determines the distance of numbers between each other in a single run of the algorithm.

Poor choices of $a,b,m$ can lead to poor randomness, producing patterns in the output vector.

$(a X_0 + b) \mod m$ should not be equal to $X_0$ , otherwise, you will have the following:

lcg(seed = 2, a = 5, b = 8, m = 16, n = 25)

##  [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

The sequence below has low periodicity, with the pattern repeating at $X_{17}$

lcg(seed = 7, a = 5, b = 3, m = 16, n = 25)

##  [1]  6  1  8 11 10  5 12 15 14  9  0  3  2 13  4  7  6  1  8 11 10  5 12 15 14

We want a very high value for the modulo $m$ so that the sequence needs to be very long before the elements repeat.

lcg(seed = 1, a = 1234, b = 9876, 
    m = 1000, n = 30)

##  [1] 110 616  20 556 980 196 740  36 300  76 660 316 820 756 780 396 540 236 100
## [20] 276 460 516 620 956 580 596 340 436 900 476

How do we make this more random?

As mentioned, this is just a pseudorandom number: every time we run the function, the output is the same.

What if we include a factor that the user (theoretically) cannot control, and may change every time the random generator is executed?

For this, we use the time of the computer.

In R, Sys.time() is a function that shows the current date time of the computer.

Sys.time()

## [1] "2025-05-13 23:01:28 PST"

If we apply the as.integer function to a POSIXct object, it gets the number of seconds since the Unix epoch (1970-01-01 00:00:00 UTC)

time_ct <- as.POSIXct("1970-01-01 00:00:00", tz = "UTC")
as.integer(time_ct)

## [1] 0

Since we are in the Philippines, this gets the number of seconds since 1970-01-01 08:00:00 PST

as.POSIXct("1970-01-01 08:00:00 PST") |> 
    as.integer()

## [1] 0

How do we make a random number out of this?

Every second that you run as.integer(Sys.time()), you will get a different number:

as.integer(Sys.time())
profvis::pause(1)
as.integer(Sys.time())
profvis::pause(1)
as.integer(Sys.time())

## [1] 1747148488
## NULL
## [1] 1747148489
## NULL
## [1] 1747148490

We will make the computer system time as our default seed number.

lcg_2 <- function(n = 1,  seed = as.integer(Sys.time())) {
    a <- 1664525
    b <- 1013904223
    m <- 2^32

    numbers <- numeric(n)  
    x <- seed
    for (i in 1:n) {
        x <- (a * x + b) %% m
        numbers[i] <- x
    }
    return(numbers)
}

Now, every second that you run the following, you will get a different result:

lcg_2(n=5)

## [1] 3755124142 3055726901 2633634064 2189308207 4060556482

If you want a fixed value every time, you just set the value of the seed number:

lcg_2(n = 5, seed = 1782)

## [1] 3980087773 3919915416 4164722711 2710257290  115743841

Uniform Random Numbers

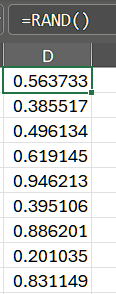
Most methods for generating random variables start with random numbers that are uniformly distributed on an interval. We denote this by $U$ .

In Excel, the function =RAND() returns a random number greater than or equal to 0 and less than 1, evenly distributed.

Now, we modify the Linear Congruential Generator such that it will only output values from 0 to 1.

Recall that the $m-1$ is the maximum possible value generated by LCG, from the properties of the modulo operator, before it circles back to 0. We normalize the generated vector $\{X_n\}$ to $[0,1]$ by dividing the elements by $m-1$ .

lcg_unif <- function(n = 1, 
                     seed = as.integer(Sys.time())) {

    a <- 1664525123
    b <- 1013904223
    m <- 2^32-1
    
    numbers <- numeric(n)  
    x <- seed
    for (i in 1:n) {
        x <- (a * x + b) %% m
        numbers[i] <- x
    }
    return(numbers/(m-1)) # normalize to [0,1]
}

lcg_unif(1)

## [1] 0.6688525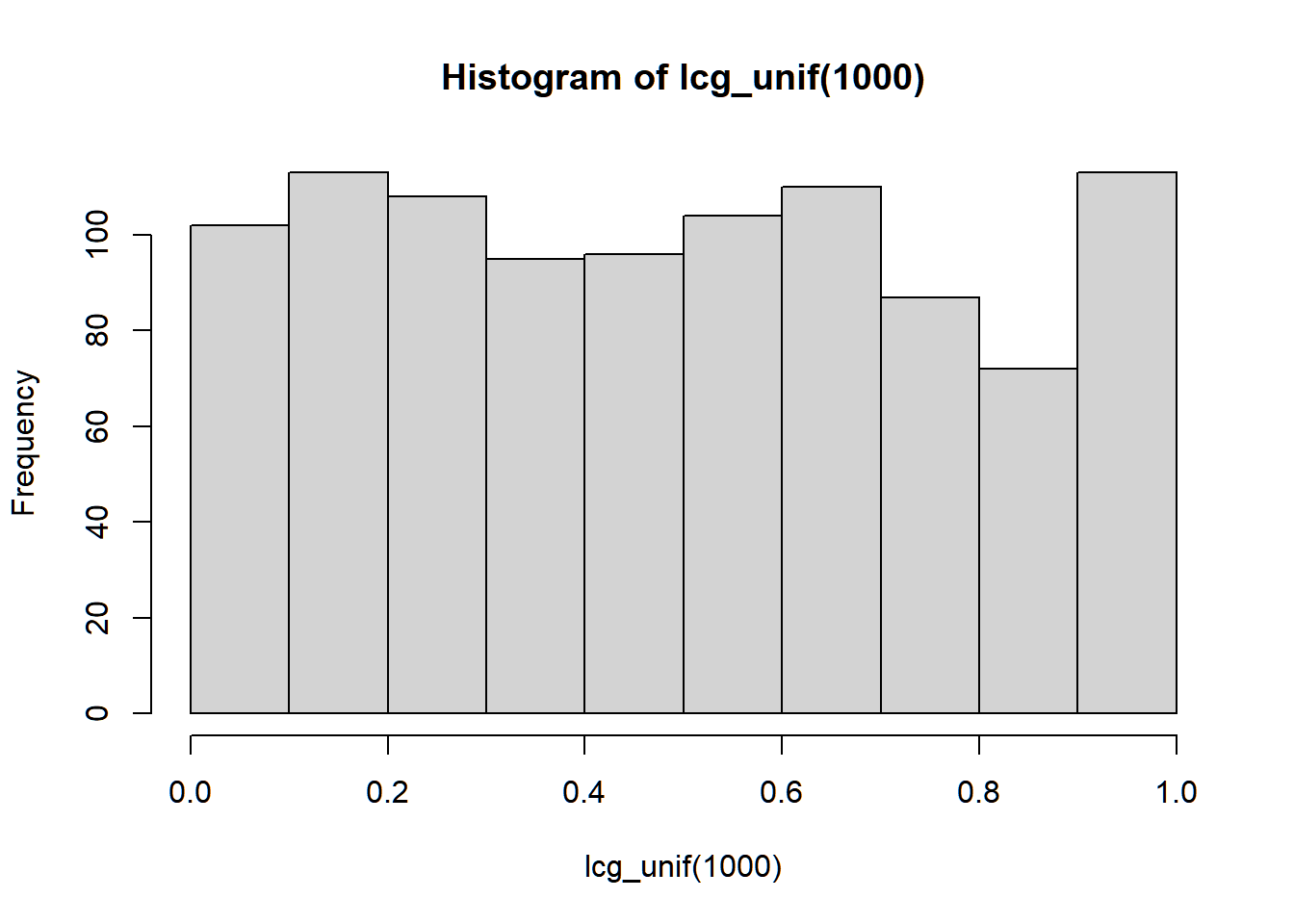

hist(lcg_unif(1000))

If $U\sim Uniform(0,1)$ , then any uniformly distributed randomly variable over an interval $a$ and $b$ may be generated by a simple transformation:

$X=(b-a)\cdot U+a \sim Uniform(a,b)$

For example, we want to generate a (continuous) random number from 10 to 20:

U <- lcg_unif(100)
X <- (20-10)*U + 10
hist(X)

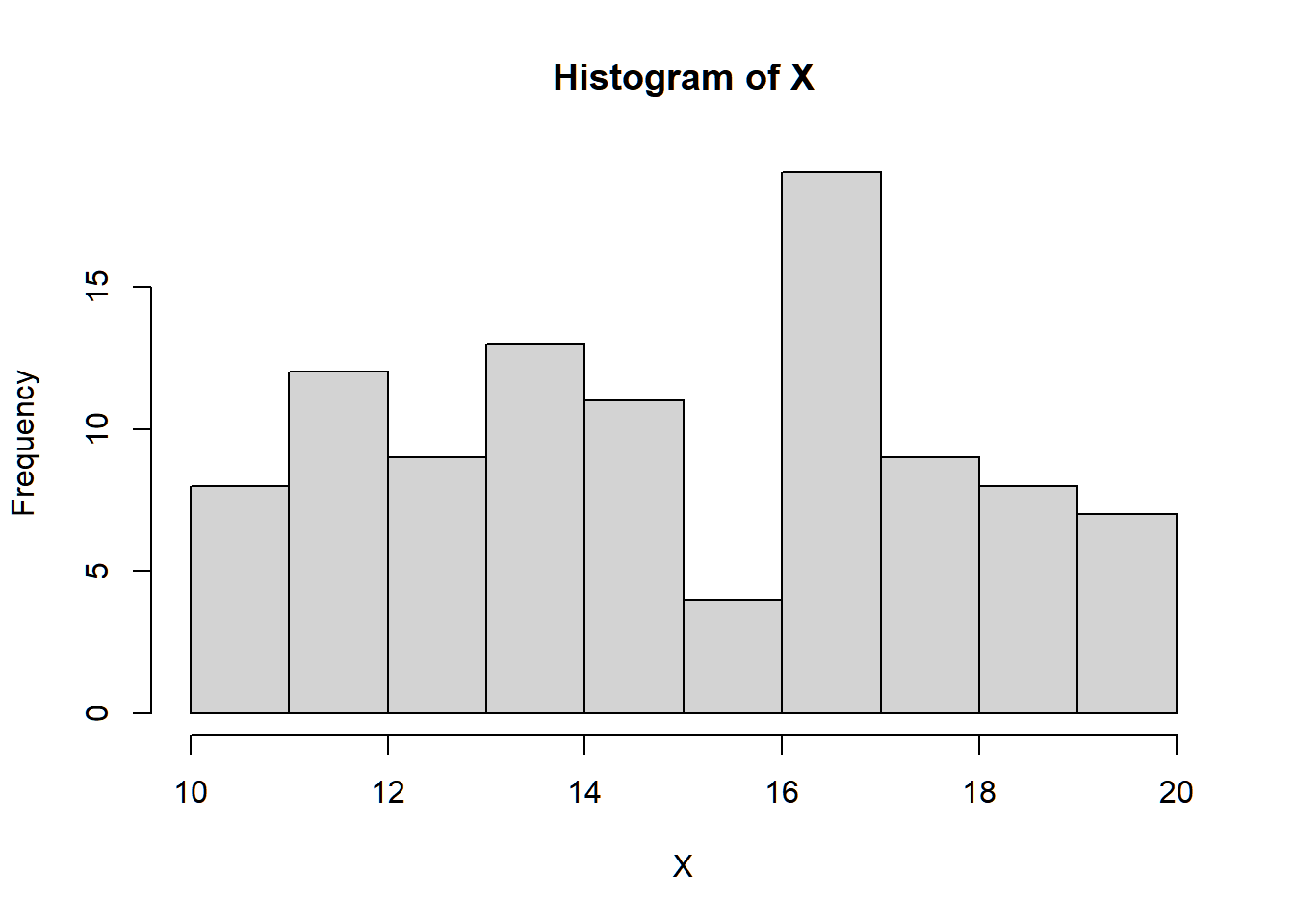
Inverse Transform Method

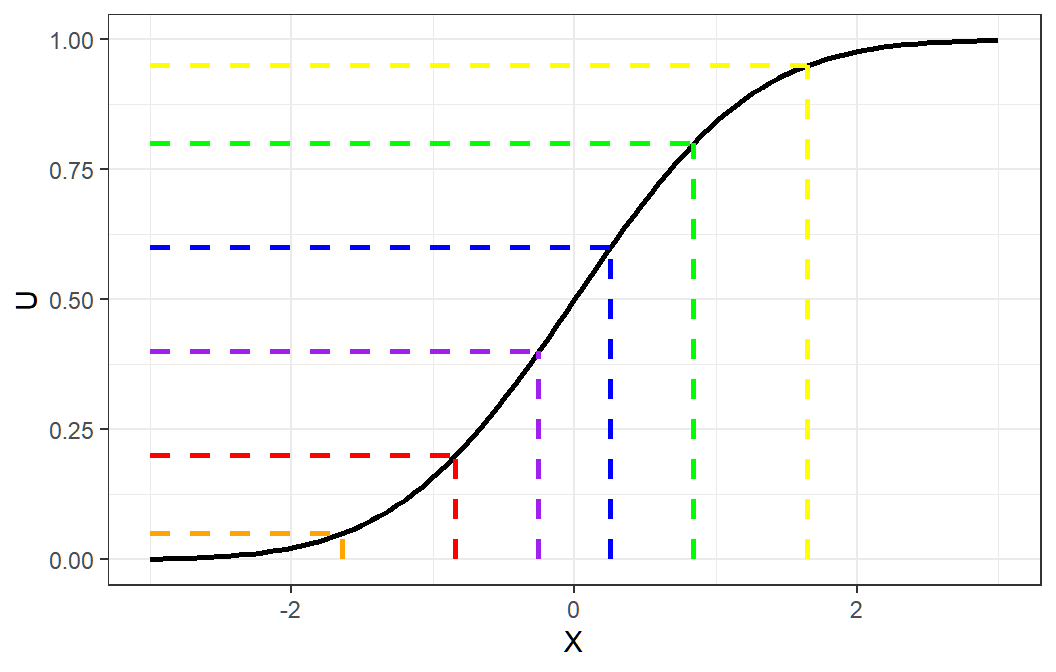
Recall Probability Integral Transform in your Stat 122 class.

Theorem 3.1 (Probability Integral Transform) If $X$ is a continuous random variable with cdf $F_X$ , then the random variable $F^{-1}(U)$ , where $U\sim Uniform(0,1)$ , has distribution $F_X$ .

We can use this concept to generate a random variable from a specified distribution, assuming that we can derive the inverse of its cumulative distribution function.

Visualization

Inverse Transform Method (Continuous Case)

Derive the expression for the inverse distribution function $F^{-1}(U)$ .
Generate standard uniform number $U$ .
Obtain desired $X$ from $X=F^{-1}(U)$

Example: Exponential Distribution

If $X \sim exponential(\lambda)$ , with cdf $F_X(x) = 1-e^{-\lambda x}$ then

$F_X^{-1}(U) = -\log(1-U)/\lambda$
U   <- lcg_unif(1000, seed = 100)
lam <- 2
X   <- -log(U)/lam
hist(X)

Inverse Transform Method (Discrete Case)

Define a probability mass function for $x_i$ , $i=1,\dots,k$ . Note that $k$ could grow infinitely.
Generate a uniform random number $U$ .
If $U\leq p_0$ , set $X=x_0$
- else if $U \leq p_0 + p_1$ , set $X = x_1$
- else if $U \leq p_0 + p_1 + p_2$ , set $X=x_2$
  
  $\vdots$
- else if $U \leq p_0 + p_1 + \cdots + p_k$ , set $X=x_k$

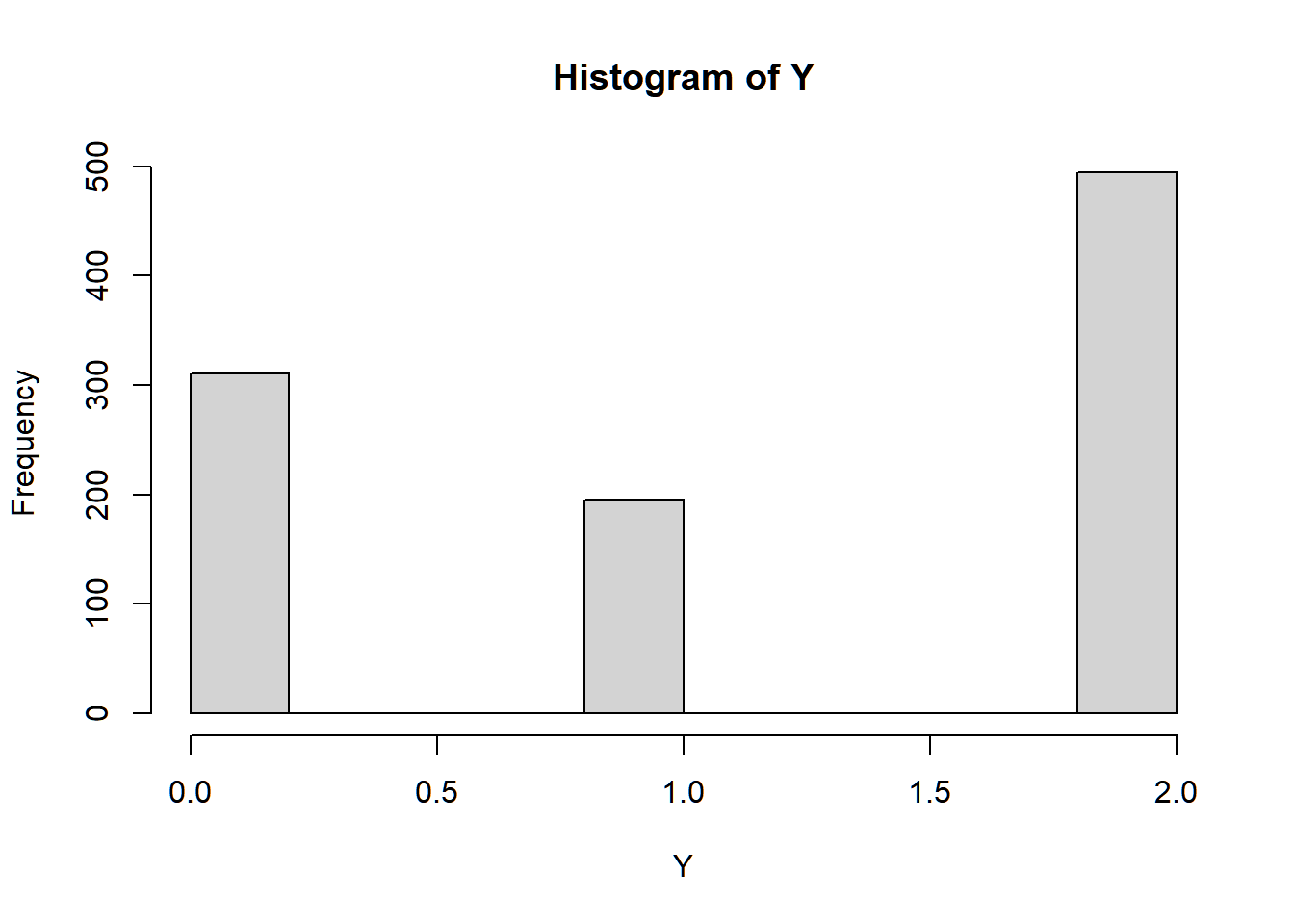
Example: Discrete Distribution

We would like to simulate a discrete random variable $Y$ that has probability mass function given by

$P(Y=0) = 0.3 \\ P(Y=1) = 0.2 \\ P(Y=2) = 0.5$

The CDF is

$F(y)=\begin{cases} 0 & y<0 \\ 0.3 & 0 \leq y < 1 \\ 0.5 & 1 \leq y < 2 \\ 1.0 & 2 \leq y \end{cases}$

We generate the random variable $Y$ according to the following scheme:

$Y=\begin{cases} 0 & U\leq 0.3 \\ 1 & 0.3 < U \leq 0.5 \\ 2 & 0.5 < U \leq 1 \end{cases}$

In R, the case_when function from the dplyr library is convenient for transforming values from a vector.
U   <- runif(1000)
Y   <- dplyr::case_when(
    U <= 0.3 ~ 0,
    U > 0.3 & U <=0.5 ~ 1,
    U > 0.5 ~ 2
)

hist(Y)

Exercise 3.1 The Cauchy Distribution has the following CDF

$F(x)=\frac{1}{\pi}\tan^{-1}\left(\frac{x-\theta}{\gamma}\right) + \frac{1}{2}$

Derive its inverse $F^{-1}(u)$ , and obtain a sample from $Cauchy(\theta=0,\gamma=1)$ . Use lcg_unif(n=1000) for generating numbers from $Unif(0,1)$ .

Box-Muller Algorithm

Again, the inverse transform method is only useful if the inverse of the CDF of a random variable has a closed form.

Recall, what is the CDF of the Normal Distribution?

The following algorithm helps us with generating numbers from a Normal Distribution, given that we can generate Uniform Random Numbers.

Definition 3.9 (Box-Muller Algorithm) Generate $U_1$ and $U_2$ , two independent $Uniform(0,1)$ random variables, and set

$R = \sqrt{-2 \log{U_1}} \quad \text{and} \quad \theta =2\pi U_2$

Then

$X = R \cos(\theta) \quad \text{and}\quad Y = R \sin (\theta)$

are independent $Normal(0,1)$ random variables.

Although we have no quick transformation for generating a single $N(0,1)$ , this is a method for generating two $N(0,1)$ random variables.

Unfortunately, solutions such as the Box-Muller algorithm are not plentiful. Moreover, they take advantage of the specific structure of certain distributions and are, thus, less applicable as general strategies.

3.2.3 Random Number Generation in R

There are built-in functions in R to generate random numbers from standard distributions like normal, uniform, binomial distributions, etc.

In the next part, we will see different functions like runif, rnorm, rbinom, and rexp to generate random numbers.

sample will also be introduced, which is used to obtain sample elements from a vector.

`runif`

In R, the runif generates a random number from a to b, inclusive.

Default range is 0 to 1.

# To get 5 uniformly distributed random numbers
set.seed(142)
runif(5)

## [1] 0.8952099 0.6990317 0.9558174 0.5615036 0.8106578

# To get 10 uniformly distributed random numbers from 5 to 50
set.seed(142)
runif(n=10, 5, 50)

##  [1] 45.28445 36.45643 48.01178 30.26766 41.47960 44.05095 17.61965 35.74645
##  [9] 24.47709 24.45205

`rnorm`

To generate numbers from a normal distribution rnorm is used, where default mean is 0 and the default standard deviation is 1.

$X_1,X_2,...,X_{10} \overset{iid}{\sim} N(0,1)$

rnorm(10)

##  [1]  1.06477887  0.71837549  0.03824233 -1.04966394  0.21231350  1.47579912
##  [7] -1.63618618  1.29561942 -0.13780914  0.49654749

$X_1,X_2,...,X_{300} \overset{iid}{\sim} N(\mu=15,\sigma^2 = 16)$

x <- rnorm(300, mean = 15, sd = 4)

ggplot(data.frame(x), aes(x)) +
    geom_histogram(aes(y=..density..), bins = 15,
                   fill = "gray", color = "black") + 
    geom_function(fun = dnorm, args = list(mean =15, sd = 4)) +
  theme_light()

## Warning: The dot-dot notation
## (`..density..`) was
## deprecated in ggplot2 3.4.0.
## ℹ Please use
##   `after_stat(density)`
##   instead.
## This warning is displayed
## once every 8 hours.
## Call
## `lifecycle::last_lifecycle_warnings()`
## to see where this warning was
## generated.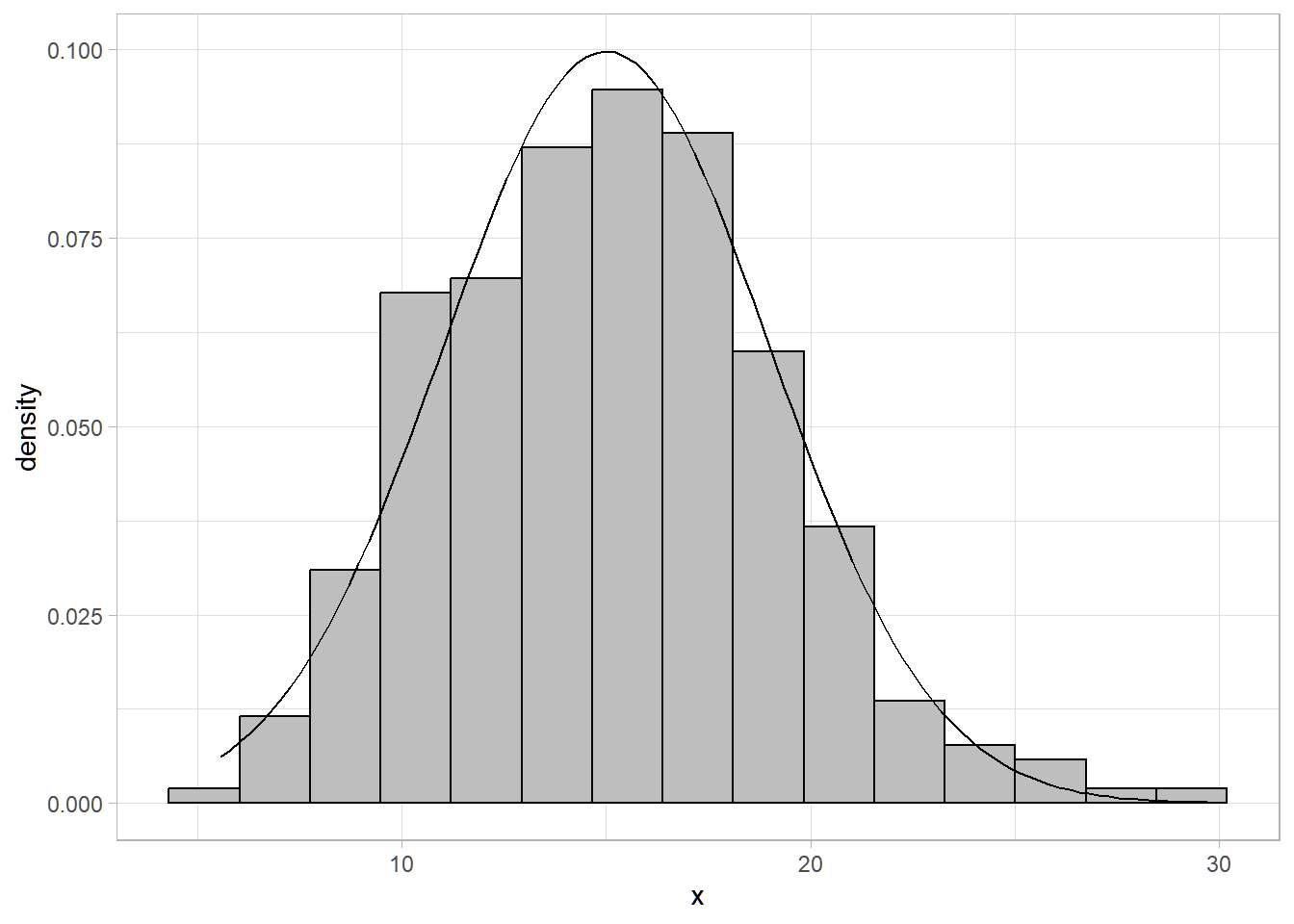

`rexp`

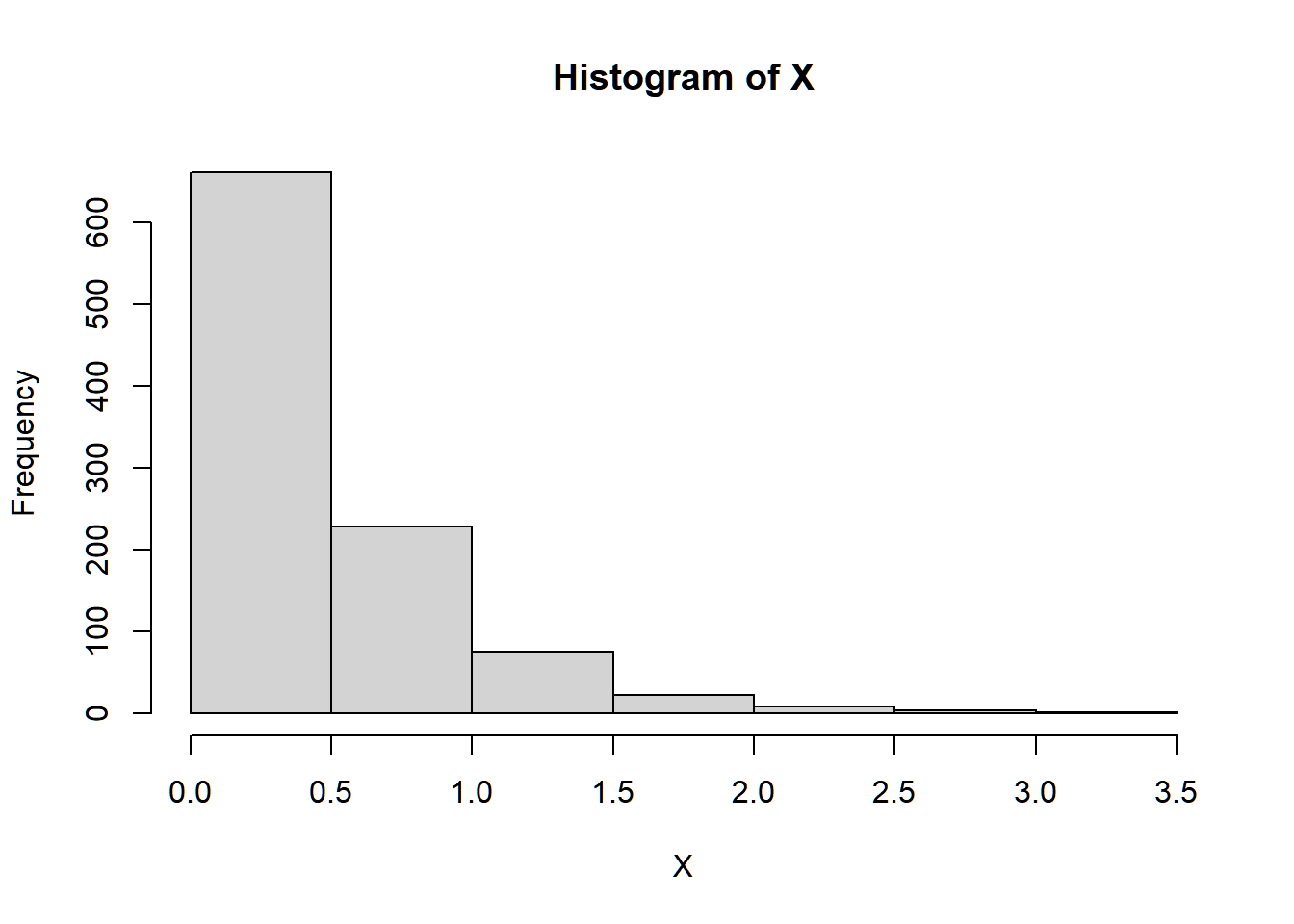
The function rexp is used to generate random numbers in which n is the number of observations or number of random numbers to be generated, rate is $λ=1/μ$ , and the numbers come from the exponential distribution with mean $μ$ .

$X_1,X_2,...,X_{20} \overset{iid}{\sim} Exp(\lambda=1/5)$

rexp(20, rate = 1/5)

##  [1]  6.3294394  0.7209384  4.2253274  5.9634621  1.2608964  0.9035019
##  [7]  1.3297511  9.4898247  3.5248339  4.5293381 12.9522758  1.4201563
## [13]  1.4115444  1.0991022  9.8878263 18.7116675  0.4939968  0.9492593
## [19]  2.0177106  3.8920139

$Y_1,Y_2,...,Y_{1000} \overset{iid}{\sim} Exp(\lambda=1/6)$

Y <- rexp(1000, 1/6)

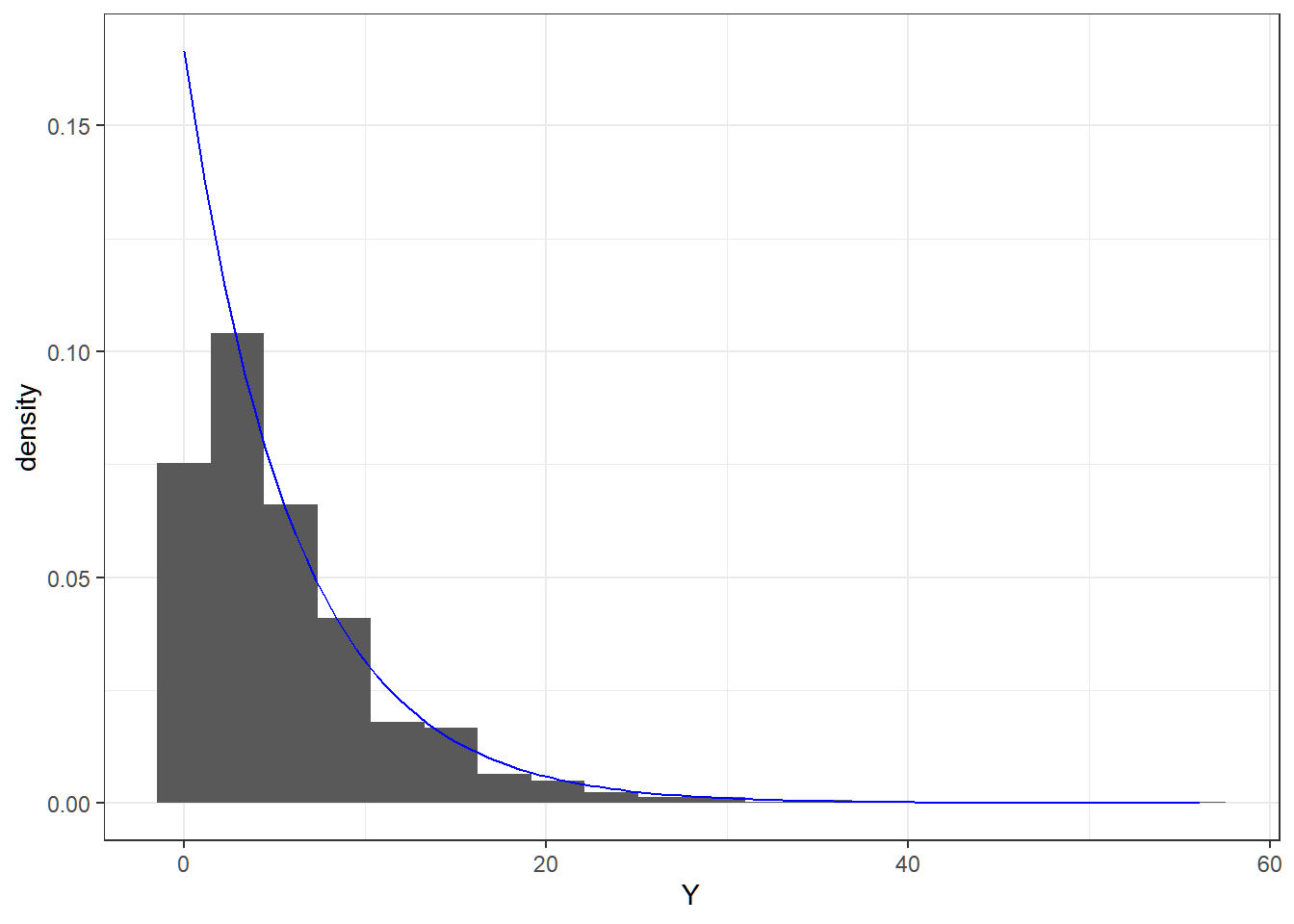
`rbinom`

The binomial random numbers are a discrete set of random numbers. To derive binomial number, value of size is changed to the desired number of trials. For instance when there were 5 trials, we set size = 5

set.seed(1)
rbinom(1, size = 5, p = 0.5)

## [1] 2

We call also have 10 binomial experiments, where each experiment has 20 Bernoulli trials, and each trial has probability of success equal to 0.2

$X_1,X_2,...,X_{10} \overset{iid}{\sim} Binom(n=20,p=0.2)$

rbinom(10,20,0.2)

##  [1] 3 4 6 2 6 7 5 4 1 2

`sample`

This function is used to generate a random element from a vector.

Generate a random name from a vector of names.

names <- c("Anna", "Betty", "Charice")
sample(names,size = 1)

## [1] "Charice"

Generate a sample of size 10 from sequence of integers from 1 to 100, without replacement:
```
sample(1:100, size = 10, replace = F)
```
```
##  [1] 97 85 21 54 74  7 73 79 99 37
```

Generate a sample of size 10 from sequence of integers from 1 to 15, with replacement:

sample(1:15, size = 10, replace = T)
sample(1:15, size = 10, replace = T)
sample(1:15, size = 10, replace = T)

##  [1]  9  9 14  5  5  2 10 14  9 12
##  [1] 15  1  4  3  6 10 10  6 15  4
##  [1] 12  4 10 12  9  7  6  9  8 12

Bernoulli Experiment, where TRUE is success, FALSE is failure, with probability of success $p=0.7$ .

sample(c(TRUE,FALSE), 
       size = 1, 
       prob = c(0.7,0.3))

## [1] TRUE

10 independent and identical Bernoulli trials. replace=T ensures that each element in the sample are IID.

sample(c(TRUE,FALSE), 
       size = 10, 
       prob = c(0.7,0.3),
       replace = T)

##  [1]  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE

Exercise 3.2 Obtaining random observations from a dataset:

Explore the dataset mtcars

It has 32 rows and 11 columns.

Obtain a random sample of size 5 by sampling from the vector 1:32, and using dataframe indexing, and the sample function.

(Optional) Acceptance Rejection Method

The problem with the Inverse Transform method is that the CDF must have a closed form and the inverse must be derivable.

This cannot be achieved in some cases.

Suppose that $X$ and $Y$ are random variables with density with density pmf $f$ and $g$ respectively, and there exists $c$ such that

$\frac{f(t)}{g(t)}\leq c$

for all $t$ such that $f(t)>0$ . Then the acceptance-rejection method (or rejection method) can be applied to generate the random variable $X$ . It is required that there is already a method to generate $Y$ .

Procedure: Acceptance-Rejection Method (Continuous Case)

Choose a density $g(y)$ that is easy to sample from, preferrably a known and common distribution.
Find a constant $c$ such that $\frac{f(t)}{g(t)}\leq c$ is satisfied.
Generate a random number $Y$ from the density $g(y)$ .
Generate a uniform random number $U$ .
If

$U\leq \frac{f(Y)}{cg(Y)}$

then accept $X = Y$ . Else, go to step 3.