Preface
“Probability? What do you mean?” - The Hitchhiker’s Guide to the Galaxy, Adams (2010)
Foreword
Late in the fall of 2016, Professor Nicholas J. Horton gave the fourth biannual David K. Pickard Memorial Lecture to the Harvard Statistics Department. Professor Horton discussed the current ‘national climate’ of Statistics in higher education, and presented this graphic:
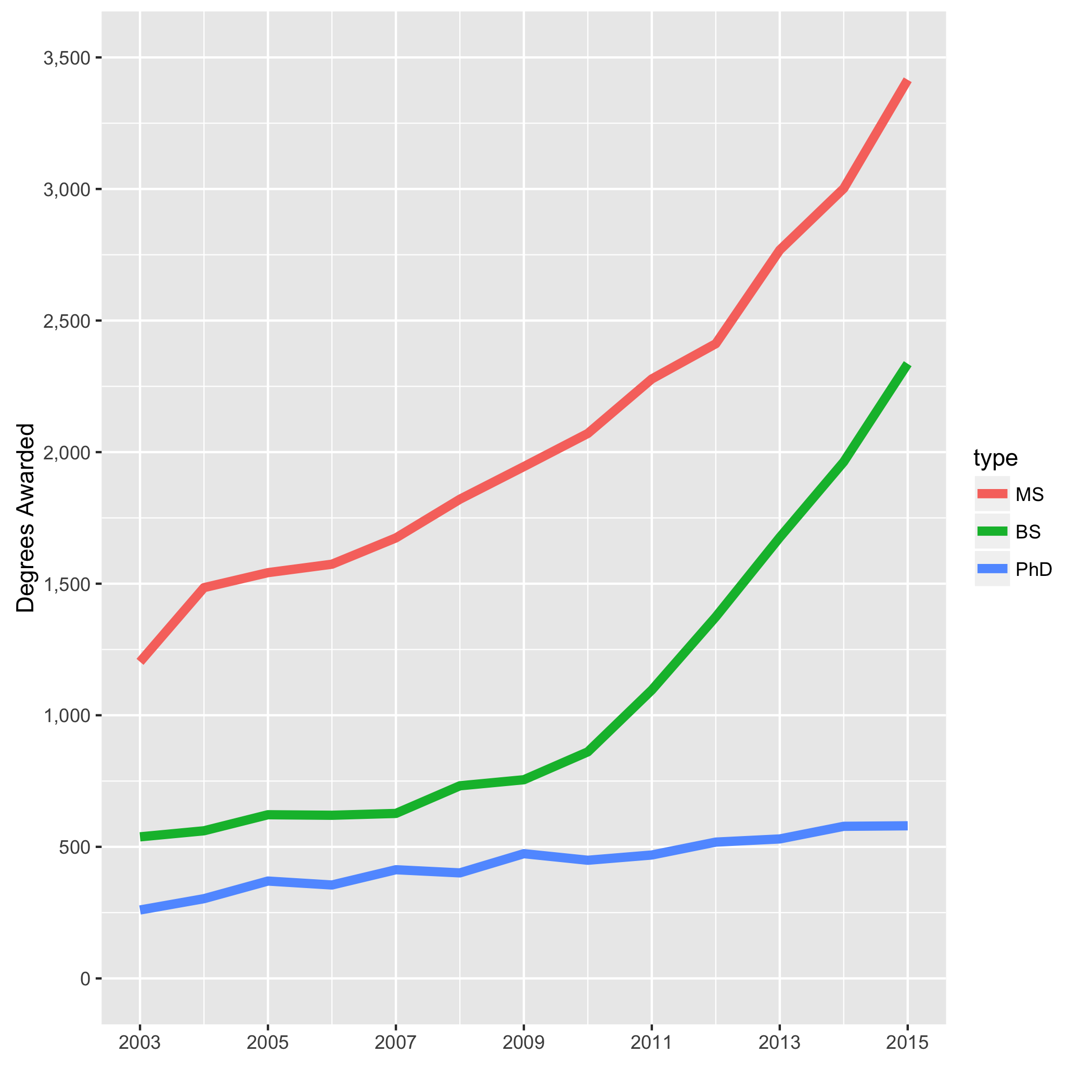
Despite the upward trend in Bachelor’s Degrees (BS) awarded annually, there still aren’t relatively many undergraduates pursuing Statistics compared to other fields of study. According to the National Center for Education Statistics (NCES), 20.5 million students were expected to attend college in 2016. We can estimate, then, that there are roughly 5 million students per grade (freshmen, sophomore, etc.), and since the above graph shows that there were about 2,300 undergraduate Statistics degrees awarded in 2015, we can approximate that about 2,300/5,000,000 < .05% of college students (less than 1 in every 2,000) focuses on Statistics. Compare this to other fields of undergraduate study - according to NCES, in the 2014-2015 academic year, there were nearly 60,000 Bachelor’s degrees awarded in “Computer and information sciences,” over 360,000 in Business, and over 95,000 in “Visual and performing arts” - and Statistics undergraduates seem a rare commodity.
However, despite the low numbers in the national context, it’s undeniable that Statistics is quickly gaining momentum as an academic field. Per the above graphic, the number of undergraduate degrees is rapidly climbing (more than quadrupled over this 12 year span), and stories with significant statistical themes and applications, like Moneyball and The Big Short, captivate national audiences (both the books - Lewis (2004), Lewis (2011) - and the movies - 2011, 2015). Statistical computing software like R and Python are gaining popularity across the nation, and analytical statistical methods dominate conversations across many disciplines, from sports to public health to finance.
Ultimately, as ‘big data’ becomes more accessible and more widely used, this rapid growth of Statistics is likely just beginning. We may well be on the forefront of a massive swell in this academic field, meaning that there is no better or more exciting time to read this book!
About this book
This book began as a thesis by Matt DosSantos DiSorbo (who you may reach at mattdisorbo@gmail.com) with Harvard Statistics Professor Joe Blitzstein. To reference the original thesis, please visit the Harvard Archives or click here (please contact Matt if you would like access). You currently reading an updated version of the book, which we are actively working on and which we hope will continue to educate students in Statistics.
The impetus for the project largely sprung from Joe’s course, Stat 110; in fact, this book can largely be considered a companion to this course. It covers many of the most interesting and important topics in introductory probability, from Counting and Combinatorics to Random Variables (both Discrete and Continuous), finishing with Markov Chains (see the table of contents on the left side of the page for a more thorough topic summary). The structure of this book is largely modeled off of Stat 110, and we will often draw on examples and explanations from lectures and other course material. The book co-written by Professor Blitzstein and Jessica Hwang, which is used in Stat 110 (Blitzstein and Hwang (2014)) often serves as a model for this book.
The writing style in this book may be described as ‘wordy.’ It certainly reads quite differently than conventional textbooks, which rarely waste words (consider the classic refrain: “this is trivial and left as an exercise to the reader”). Indeed, if you are already familiar and comfortable with this material, the prose of this book may feel inelegant, excessive and even awkward. However, for students who are new to these concepts, excessive explanation can often be a blessing. While the elegance of textbooks may please the authors (who are themselves masters of the material) it can frustrate students; this is too often forgotten in classrooms around the country. Ultimately, under-explaining is far worse than over-explaining, and therefore we will risk the latter. In general, this book will subvert many themes of conventional textbooks (minimal use of propositions, theorems, proofs, etc.) in an effort to produce a streamlined, engaging narrative for students who are new to the ‘language’ of rigorous Statistics.
This book is primarily a teaching tool, and thus we are not very concerned with proofs unless they promote understanding. Therefore, we will generally only present proofs when they allow us to practice our mastery of the material or shed light on a specific concept. The only prerequisite for this book is knowledge of math up to multivariable calculus. However, if you do not know multivariable calculus but are very familiar with single variable calculus, this book may be manageable; ‘multivariable’ calculus only shows up when we take multiple derivatives and integrals, which is very easily generalizable from the one-dimensional case (instead of taking just one derivative, take a few more!). There are no Statistics or linear algebra prerequisites (we will work a bit with matrices, but at a low level and always with thorough explanation).
The book is currently undergoing a ‘dynamic editing’ phase; that is, we would love to get your input, comments and corrections. At the start of every chapter, you will notice a link that will direct you to a form designed to mark your feedback. Please do not hesitate to contribute; every suggestion, large or small, helps to improve the book and thus ease the learning process for future students.
Further, since this book was originally launched, other works have been developed as part of a series dedicated to providing free and open access to educational resources for topics in Statistics. Specifically, you can find further study in Introductory Statistics, Inference and Stochastic Processes.
Features
This book is intended to engage with the young, modern reader, largely by leveraging the capacities of an online interface. If you asked the average student to list their mental associations with the word “Statistics,” they might conjure up images of dry textbooks, terse theorems and stuffy explanations (many will recall thumbing through pages of Normal distribution tables in their high school AP Statistics class to find a p-value). The goal of this book is to make Statistics ‘sexy’ again; to present the material, without sacrificing its integrity, in new and exciting ways.
This book is written in R Bookdown, an extension of R Markdown used for, well, writing books. This interface allows us to link to external pages, cross-reference within the book (i.e., you can easily skip to Chapter 1), present dynamic aesthetics (be sure to toggle the font/page options at the top of your screen), implement rapid search and navigation (table of contents is on the left side of the page), and streamline the citation process (i.e., see Xie (2016) for much more on using Bookdown).
This book will explore and present data science techniques using R, a popular statistical computing software, in addition to discussing theoretical probability. Each chapter includes chunks of R code that explore our results via simulation, generate data, produce graphics, etc. In this way, R can be a vital tool because it helps to build intuition and even checks our results in difficult cases (if you don’t know the answer to something, you can almost always simulate it!). Within the book itself, R sections will be clearly marked and separated from the rest of the text. Here, we calculate \(2 + 2\) using R and print the output:
2 + 2## [1] 4As well as in-chapter problems and examples, this book provides problems at the end of each chapter to help the reader develop relevant skills; these problems can be solved with analytical approaches (i.e., solved with pencil and paper) and empirical approaches (i.e., solved or approximated with a simulation or calculation in R). Many problems from Blitzstein and Hwang (2014) are restated here; the analytical solutions to these selected problems are freely available online (which is why they were selected to be restated in this book). In addition, many new problems are presented in this book (again, nearly all of them have both analytical and empirical solutions).
Bookdown allows us to include Shiny applications, which are interactive tools that we will use to help build intuition. We are working on being able to embed the applications directly into the Bookdown interface; for now, however, they will be available at an external source. In the current version of the book, we will instead have ‘tutorial’ videos that provide demonstrations for each of the applications. You can freely download the relevant code to run these applications on your local machine here. For help on the installation process, you can reference this tutorial. One of the tutorial videos is presented below to demonstrate the general layout of a Shiny application; of course, we do not expect you to understand the theory behind this application yet!
Click here to watch this video in your browser. As always, you can download the code for these applications here.
The art for this book was created in Sketchpad. Finally, to maintain as much of the human element as possible, we will include instructional videos that focus on specific topics and concepts:
Acknowledgements
This project would not be possible without the hard work, dedication and support of many, many people.
First, we thank Jessica Hwang for her incredible work on the textbook co-written with Professor Blitzstein. This book, titled “Introduction to Probability” (Blitzstein and Hwang (2014)), was an enormous help for this project, and will be referenced many times. We also thank Yihui Xie, who graciously created and shared his base R Bookdown template, as well as authoring a book about writing in R Bookdown (Xie (2016)).
We are in debt to a great number of Harvard Professors and Teaching Staff for their guidance: Mike Parzen, Mayumi Marimoto, Kevin Rader, Samuel Kou, Edo Airoldi, William Chen, Jimmy Looney, Ryan Lee, Angela Fan, Advik Shreekumar, Theresa Gebert, Grace Young, Peter Der Manuelian, Joshua Walton, Gregory Nagy, David Elmer, Sergios Paschalis, John Coglianese and David Johnson. Many provided revisions, advice and support for the project; specifically, we thank Peter Tu, Matt Goldberg, Dan Fulop, Nathaniel Ver Steeg, Jimmy Loomos, David Steinbach, Peter Wu, Sanjey Sivanesan, Simon Merriweather, Lucas Farewell, Josh Friedman, Bo Yarabe, Tarek Austin, Andrew Wyner, Marlee Ehrlich, Mike Ross, Stephen Turban, Nayiri Ayanian, Katherine Cohen, Sinclair Bush, Daniel Evans, Alec Lotstein, Patrick Keegan, Matt Draper, Isaac Abreu, Dwight Harris, Nina Fournier, Dan Czuchta, the Zacchio Family, Nathan Nye, Cameron Flower, Ben Kulas, Bernie Horovitz, Eric Kirsten, Scott, Liz, Tony and Linda Santos, Leo, Steve and Domenic DiSorbo, Jim Barone, and Maura Duggan, as well as the many Stat 110 students over the years.
A special thanks to Renan Carneiro, Juan Perdomo, CJ Christian, Nicholas Larus-Stone, Demren Sinik, Anne, Tony, Tommy and Sammy DiSorbo.
Dedication
This book is currently in a ‘dynamic editing’ stage and we are asking for edits from our readers; this version, then, is dedicated to you!