Chapter 2 Conditional Probability

“Smoking is one of the leading causes of statistics.” -Fletcher Knebel

We are currently in the process of editing Probability! and welcome your input. If you see any typos, potential edits or changes in this Chapter, please note them here.

Motivation

‘Thinking conditionally,’ that is, thinking given certain information, is one of the most important concepts discussed in this book. In this chapter, we will engage in some of the basics of conditional probability and the associated concepts. We will also delve further into one of the largest topics of this book: Random Variables. Specifically, we will start with Binomial Random Variables.

Conditional Probability

Recall in Chapter 1 that we began to work with probability; however, we only operated in a ‘naive’ setting. That is, we worked with cases where we assumed that all outcomes were equally likely: i.e., coin flips. die rolls, etc. It was ok, then, to just use the naive definition of probability: count all of the favorable outcomes and divide by the number of total outcomes (in turn, this required us to learn a variety of counting methods and strategies). However, it’s clear that outcomes are often not equally likely, or that the probabilities of certain events depend on the outcomes of other events. This is why we need conditional probability. In our notation, $P(A|B)$ means “the probability of $A$ given that $B$ occurred.”

Let’s consider an example. Say a Professor is interested in the probability that over 300 students take his class next semester. Well, this is likely conditional on the ratings that his previous students have given the class (if you see a class is poorly rated, you’re less likely to take it). So, we could say that given the fact that his ratings were very poor, the probability that the Professor has over 300 students drops.

In general, we can define the probability that event $A$ occurs given that event $B$ occurred as:

\[P(A|B) = \frac{P(A \cap B)}{P(B)}\]

Recall that $A \cap B$ is the intersection of $A$ and $B$ (the middle part of the Venn Diagram), so $P(A \cap B)$ is the probability that both $A$ and $B$ occur. When we condition on $B$ occurring, then, we are simply parsing down a sample space: reducing the entire sample space to the space when $B$ occurs. Within this space of ‘$B$ occurring,’ the space where $A$ occurs is clearly the intersection of $A$ and $B$ (it’s a given that $B$ has occurred, so if $A$ occurs it must be the intersection), and then we divide by the total ‘size’ of the ‘new’ sample space, or the probability of $B$. From this concept, many complexities arise.

Concept 2.1 Law of Total Probability:

For two events $B$ and $A$, you can find the overall probability of $A$ using the following formula:

\[P(A) = P(A|B)P(B) + P(A|B^c)P(B^c)\]

Take a minute to convince yourself why this makes sense. We are simply parsing down $A$ into two cases: when $B$ occurs and when $B$ does not occur. We take the conditional probabilities of each case, and then weight them by the probability that we are in that space ($P(B)$ and $P(B^c)$). Indeed, you can think of LOTP as a weighted average! In this case, we consider two cases (when $B$ occurs and when $B$ does not occur) but we can continue to split the probability into more cases if necessary.

Let’s consider a specific example. Anne is an accountant. She lives in rural Connecticut and has to walk to work every day, which means that the probability she goes to work is reliant on the weather. If it is sunny, she will go to work with probability .95. If it is raining, she will go to work with probability .3. Imagine that, on any given day, there is a .6 probability that it is sunny.

Let $P(W)$ be the probability that she goes to work, and $P(S)$ be the probability that it is sunny. Intuitively, if we want to find $P(W)$, we can break the probability into two cases: when $S$ occurs and when $S^c$ occurs (remember, $S^c$ means that ‘$S$ does not occur’). By employing LOTP, we get:

\[P(W) = P(W|S)P(S) + P(W|S^c)P(S^c)\] \[= .95 \cdot .6 + .3 \cdot .4 = .69\]

Intuitively, Anne goes to work 95% of the time on sunny days, and 30% of the time on rainy days, so we weight these cases accordingly.

We can confirm our intuition with a simulation in R. We will create vectors that we will fill with 0 or 1 (based on the outcome of a random simulation that tells us if the above events occur); 0 means that the event didn’t occur, 1 means that it did. This ‘binary’ vector is a useful convention, since we only have to take the mean of the vector to find the empirical probability of the event (i.e., if a vector has half 1’s and half 0’s, then the mean is 1/2, correctly implying that the event occurred 50% of the time). Recall that we can use runif(1) to generate a random number between 0 and 1; this allows us to simulate the above events (i.e., if runif(1) spits out a value less than .6, we say it is a sunny day, and if it spits out a value greater than .4, we say it is a rainy day). We will discuss more about what runif, or ‘generating a random value from a Uniform distribution,’ actually means in Chapter 4.

#replicate
set.seed(110)
sims = 1000


#create vectors to track if it is sunny/if Anne goes to work
sun = rep(0, sims)
work = rep(0, sims)


#run the loop
for(i in 1:sims){
  
  #flip to see what the weather is
  weather = runif(1)
  
  #flip to see if Anne goes to work
  go = runif(1)
  
  #the case where it is sunny
  if(weather <= .6){
    
    #mark that it was sunny
    sun[i] = 1
    
    #Anne goes to work with probability .95 in this case
    if(go <= .95){
      work[i] = 1
    }    
  }
  
  #the case where it is rainy
  if(weather > .4){
    
    #Anne goes to work with probability .3 in this case
    if(go <= .3){
      work[i] = 1
    }
  }
}

#we should get .6 for sun and .69 for work
mean(sun); mean(work)

## [1] 0.639

## [1] 0.705

Concept 2.2 Bayes’ Rule:

For our purposes, Bayes’ Rule provides a useful way of going between $P(A|B)$ and $P(B|A)$; on a larger scale, it is the cornerstone of an entire field within Statistics (‘Bayesian Statistics’). The formula is as follows:

\[P(A|B) = \frac{P(B|A)P(A)}{P(B)}\]

Note how we get this formula: we know that $P(A|B) = \frac{P(A \cap B)}{P(B)}$ by the definition of conditional probability from above, and we can then get $P(A|B)P(B) = P(A \cap B)$ if we multiply both sides by $P(B)$. Then, by symmetry, we know that $P(A|B)P(B) = P(B|A)P(A)$. Dividing everything by $P(B)$ gives the formula above.

However, we often write the marginal $P(B)$ in the denominator by using the Law of Total Probability, simply because it’s often easier to calculate in actual examples. So, the more common form of Bayes’ Rule is:

\[P(A|B) = \frac{P(B|A)P(A)}{P(A)P(B|A) + P(A^c)P(B|A^c)}\]

Bayes’ rule is an enormous part of Statistics, as mentioned above: Bayesian Statistical methods are becoming wildly more popular in the academic and professional worlds.

Let’s consider an example. Frodo needs to return a piece of jewelry to the store (Mordor Arts & Crafts, Inc.). His friend, Sam, has a car, and if Sam goes with Frodo, there is a .9 probability that Frodo gets the jewelry to the store. However, if Sam doesn’t go with Frodo (and Frodo must get there by himself), he only has a .1 probability of making it to the store. Sam is a good friend, and there is a .8 probability that he goes with Frodo. Conditioned on the fact that Frodo successfully returned the jewelry to Mordor, what is the probability that Sam went with him?

This is a classic example of Bayes’ Rule. Let $F$ be the event that Frodo gets the jewelry to the store, and $S$ be the event that Sam goes with Frodo to the store. We are interested in $P(S|F)$, which, using the definition of Bayes’ Rule, we can write as:

\[P(S|F) = \frac{P(F|S)P(S)}{P(F)}\]

The terms in the numerator of the RHS are relatively straightforward to find: based on the prompt, we are given $P(F|S) = .9$ (if Sam comes, Frodo has a .9 probability of making it) and $P(S) = .8$ (Sam has a .8 probability of coming). We aren’t given the denominator $P(F)$, though, and to find this we will have to employ LOTP (recall that we discussed how this form, Bayes’ Rule with the LOTP expansion in the denominator, is more ‘useful’ in general).

\[P(S|F) = \frac{P(F|S)P(S)}{P(F|S)P(S) + P(F|S^c)P(S^c)}\]

The two ‘new’ terms are given to us in the prompt: $P(F|S^c) = .1$ (if Sam doesn’t go, Frodo only has a .1 probability of making it) and $P(S^c) = .2$ (Sam has a .8 probability of going, so he has a .2 probability of not going). Plugging in:

\[=\frac{.9 \cdot .8}{.9 \cdot .8 + .1 \cdot .2} = .97\]

It makes sense that this probability is high; Frodo has a very good chance of making it if Sam is with him, and a very bad chance of making it if Sam is not with him, so if he made it, Sam was probably there! In addition, Sam had a pretty high probability of coming (.8) to start out with (although note that the probability that Sam came increased from the .8 baseline, which is intuitive).

We can confirm our intuition with a simulation in R. As before, we will fill vectors with 0 or 1 to indicate if the events in question occurred or didn’t occur, respectively.

#replicate
set.seed(110)
sims = 1000

#set paths for Sam coming/Frodo making it
Sam = rep(0, sims)
Frodo = rep(0, sims)

#run the loop
for(i in 1:sims){
  
  #flip for each Sam and Frodo
  Sam.flip = runif(1)
  Frodo.flip = runif(1)
  
  #the case where Sam comes
  if(Sam.flip <= .8){
    
    #mark that Sam came
    Sam[i] = 1
    
    #Frodo makes it with .9 probability
    if(Frodo.flip <= .9){
      Frodo[i] = 1
    }
  }
  
  #the case where Sam didn't come
  if(Sam.flip > .8){
    
    #Frodo makes it with .1 probability
    if(Frodo.flip <= .1){
      Frodo[i] = 1
    }
  }
}

#should get .8 overall for Sam
mean(Sam)

## [1] 0.829

#find the mean of Sam conditioned on Frodo making it; should get .97
mean(Sam[Frodo == 1])

## [1] 0.9789196

Concept 2.3 (Inclusion/Exclusion):

This is a very useful way to find the probability of the union of multiple events. Remember that the union of two sets is essentially the entire Venn Diagram (each set by itself, and then the intersection of the two sets, or the middle part of the diagram). Just imagine extending this concept to more than two events or sets; like a Venn Diagram but with more than two circles. If we’re interested in finding the probability of a union, the simplest form (where we have two sets) is:

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

If we want to extend this probability to more than two sets, we use the form:

\[P(Union \; of \; Many \; Events) = P(Singles) -P(Doubles) + P(Triples) - P(Quadruples)...\]

The reason why we’re doing this is because, as so often is the case, we need to adjust for overcounting. Consider the simplest case when we are interested in finding $P(A \cup B)$. When we add the marginal probabilities, $P(A)$ and $P(B)$ (which we denote as $Singles$ above), we are double counting the intersection $P(A \cap B)$. Since, by definition, this intersection is in both $A$ and $B$, we add it twice (once when we add each marginal probability), when we only want to add it once. Therefore, we have to subtract out the $Double$, or the intersection $P(A \cap B)$, so that we are only adding it once. This adding/subtracting pattern continues ad nauseam as you add more and more events, which is how we get the general formula above. Importantly, you might not always have just one $Double$, $Triple$, etc. For example, in a Venn Diagram with three circles $A$, $B$ and $C$, there are ${3 \choose 2} = 3$ possible doubles: $P(A \cap B)$, $P(A \cap C)$ and $P(B \cap C)$. Here, we would just have to add all of the probabilities, as we’ve been doing with the singles; that is, $P(Doubles)$ represents more than just one term!

Inclusion/Exclusion is far easier to understand with a visual explanation:

Click here to watch this video in your browser.

Now consider an example that is very similar in structure to ‘de Montmort’s matching problem,’ a classic example fully discussed here by Professor Joe Blitzstein. There are $n$ couples at the hospital, and each has 1 baby (for a total of $n$ babies). All of the couples leave their babies in the hospital and go home to rest, and come back in the morning to pick up their babies. However, there is a horrible mix-up in the nursery, and each couple is simply given a random baby. Let $A$ be the probability that at least one couple gets their baby back. Find $P(A)$.

This is a very interesting problem with many applications: in later chapters, we will discuss how to find how many couples get their baby back on average (the Expectation, as we will then define it). It’s not immediately obvious why this is any different from the birthday problem (which we will see below): we are just sampling babies instead of days, and we are still looking for the probability of a ‘match.’ However, consider that we are now sampling without replacement (once you give a baby out, the baby is gone) as opposed to sampling with replacement in the birthday problem (there can be as many birthdays on a single day as you like; i.e., that day can be ‘sampled’ over and over again). Also, the ‘matches’ here are fundamentally different: we need the correct couple to pick the correct baby, not for multiple people to be born on an arbitrary day (these comparisons will make more sense when you refer to the ‘birthday problem’ section later in this chapter).

In any case, as you might have guessed, we can solve this problem using Inclusion-Exclusion. That’s because $A$ is the union of many events; specifically, $A = A_1 \cup A_2 \cup ... \cup A_n$, where $A_i$ is the event that the $i^{th}$ couple gets their baby back. In general, if a union occurs, then we know that ‘at least one event’ occurred, and here we want the probability of ‘at least one couple’ getting their baby back. With $A$ defined in this way, we can write, straight from the definition of Inclusion-Exclusion:

\[P(A) = P(A_1) + P(A_2) + ... + P(A_n) - P(A_1 \cap A_2) - P(A_1 \cap A_3) - ... - P(A_{n - 1} \cap A_n) + ...\]

Remember, we just have to add all of the ‘singles,’ then subtract all of the ‘double’ intersections, all the way up to the ‘$n$-way’ intersection. It might seem like this could be computationally intense, but we now have a perfect opportunity to use symmetry. That is, there’s no reason to think that $P(A_1)$ is different from $P(A_{14})$, or $P(A_2 \cap A_3)$ is different from $P(A_1 \cap A_9)$. Since the set-up of the problem is completely symmetric with respect to all of the different couples, we expect these probabilities to be the same by symmetry. Therefore, we can combine the terms (i.e., we have $n$ ‘singles,’ so we can just write $nP(A_1)$). Recall that for a $k$-way intersection, we have ${n \choose k}$ possible combinations.

\[P(A) = nP(A_1) - {n \choose 2}P(A_1 \cap A_2) + ...\]

Now, we simply have to find the probability of a $k$-way intersection. That is, what is $P(A_1 \cap A_2 \cap ... \cap A_k)$ for any $k$? Consider $P(A_1 \cap A_2)$. We can employ the naive definition of probability. In the denominator, there are $n!$ total ways to hand out the babies to the parents (since there are $n!$ ways to line the babies up). The numerator is a bit trickier. If we know that $A_1$ and $A_2$ occurred, that means the first two couples got their baby back, which means the first two babies are accounted for. There are then $(n - 2)!$ ways to arrange the rest of the $n - 2$ babies among the $n - 2$ remaining couples. So, we get $P(A_1 \cap A_2) = \frac{(n - 2)!}{n!}$ and, in the more general case, $P(A_1 \cap A_2 \cap ... \cap A_k) = \frac{(n - k)!}{n!}$. Consider this in the simple and extreme cases. We get $\frac{(n - 1)!}{n!} = 1/n$ when $k = 1$; this makes sense, because the probability that the first couple gets their baby is just $1/n$ (there are $n$ babies, and only one of them is their baby). We get $\frac{(n - n)!}{n!} = 1/n!$, since $0! = 1$, in the case where $k = n$. This also makes sense; there are $n!$ ways to line the babies up, and only one way results in every single couple getting their baby back. If we expand the binomial coefficient term in the above formula, we can then write:

\[P(A) = \frac{n(n - 1)!}{n!} - \frac{n!}{(n - 2)! 2!} \frac{(n - 2)!}{n!} + \] \[=1 - \frac{1}{2!} +...\]

We can write this sequence in a summation (if you’re not convinced, try writing a few more terms):

\[\sum_{k = 1}^n (\frac{1}{k!})\cdot(-1)^{k + 1}\]

Why the $(-1)^{k + 1}$ term? We want the sign of our series to alternate, and here we are raising $-1$ to alternating powers and thus alternating the sign. We want to start with a positive value, so we have $k + 1$ in the exponent (we start the sum at $k = 1$, and thus get $(-1)^2 = 1$ in the first term).

Does this sum simplify? Well, recall the Taylor Series expansion for $e^x$ (if you are rusty, you can find an excellent cheatsheet on Taylor Series here).

\[e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ...\]

Now imagine plugging in $x = -1$:

\[e^{-1} = 1/e = 1 - 1 + \frac{1}{2!} - \frac{1}{3!} + ...\] \[\frac{1}{2!} - \frac{1}{3!} + ...\]

If we compare this to our above answer of $P(A) = \sum_{k = 1}^n (\frac{1}{k!})\cdot(-1)^{k + 1}$, we quickly see that:

\[P(A) \approx 1 - 1/e\]

For large $n$ (write out the first few terms in the $P(A)$ sum to convince yourself).

Phew! That was a lot of work, but we got a pretty neat result: as $n$ grows, the probability of at least one match (which we notated as $P(A)$ in this problem) approaches $1 - 1/e$. It’s pretty incredible how this famous mathematical constant showed up in this problem! We can confirm the work we’ve done here with a simulation in R, and compare the empirical probability of matches with the analytical result we’ve seen. Notice how both the empirical and analytical results quickly approach the asymptotic result of $1 - 1/e$, and the empirical result is slightly more jagged (it is, after all, a random simulation).

#replicate
set.seed(110)
sims = 1000

#define different values of n to iterate over
n = 2:10

#set paths for the empirical and analytical solutions
sol.a = rep(NA, length(n))
sol.e = rep(NA, length(n))

#iterate over n
for(j in 1:length(n)){
  
  #first, calculate the analytical solution
  k = 1:n[j]
  sol.a[j] = sum((1/factorial(k))*(-1)^(k + 1))
  
  #now run the empirical simulation
  #indicate if we get a match or not
  match = rep(0, sims)
  
  #run the loop
  for(i in 1:sims){
    
    #generate the 'random order' to give the babies out
    babies = sample(1:n[j])
    
    #calculate 'ratios' of couple-to-baby. If the couple gets
    #   their baby, ratio should be 1
    ratios = babies/(1:n[j])
    
    #see if we got a match (at least 1 ratio is 1)
    if(length(ratios[ratios == 1]) > 0){
      match[i] = 1
    }
  }
  
  #mark the empirical probability
  sol.e[j] = mean(match)
}



#graphics
plot(n, sol.a, main = "Hospital Matching Problem",
     xlab = "n", ylab = "P(At Least One Match)",
     type = "p", lwd = 3, col = "firebrick3",
     ylim = c(0, 1), pch = 16)
lines(n, sol.e, col = "black", lwd = 3, 
  type = "p", pch = 16)

#put in the asymptotic result
abline(h = 1 - 1/exp(1))

#legend
legend("topright", legend = c("Empirical Result", "Analytical Result"),
       lty=c(2,2), lwd=c(2.5,2.5),
       col=c("black", "red"))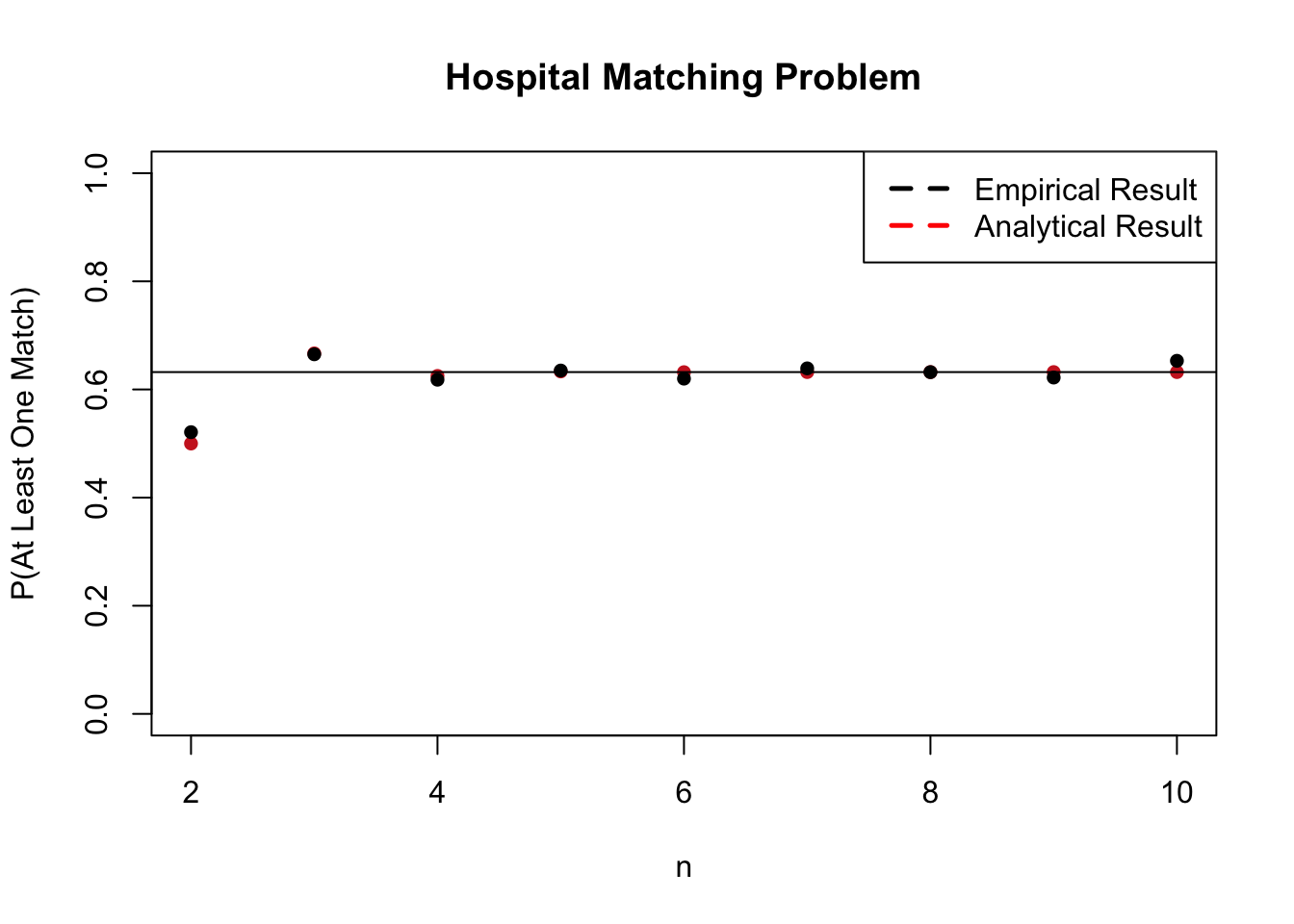

Concept 2.4 (Independence):

Two events are independent if knowing the outcome of one event does not affect the probability of the other event occurring. Let’s consider trivial examples in a couple of cases. Two seemingly independent events are $H$, the event that my little brother grows an inch this year, and $G$, the event that the Boston Red Sox win the World Series this year. Unless there is some crazy butterfly effect, it is safe to say that these events are independent: my brother does not play for the Red Sox, and thus his growing an inch does not affect the Red Sox (nor will a Red Sox World Series championship ‘inspire’ him to grow an extra inch!). Knowing that he has grown an inch does not affect the probability that the Boston baseball team will bring home the hardware, and vice versa.

Two events that may be dependent (not independent) are $S$, the event that a nasty snowstorm occurs, and $C$, the event where someone gets in a car crash. It make sense that if $S$ occurs, then $C$ will be more likely. Likewise, you could imagine that if you heard that someone gets in a car crash without knowing the weather outside (you observe $C$), you might imagine that it was more likely to be snowing ($S$ occurs).

So, let’s define this with notation. If events $A$ and $B$ are independent, we can say:

\[P(A|B) = P(A), P(B|A) = P(B)\]

This basically means that the conditional probability of $A$ given $B$, or the probability that $A$ occurs given that $B$ occurred, is the same as the marginal probability of $A$ (and vice versa for $B$ given $A$). That is, thinking conditionally gives us no extra information about an event occurring. This makes sense, because we know that if two events are independent, then the occurrence of one does not affect the other, so this conditioning doesn’t change the probability of the event.

We can also apply this logic to intersections. We know that, by rearranging the equation $P(A|B) = \frac{P(A \cap B)}{P(B)}$ for conditional probability (multiplying both sides by $P(B)$), we can get an expression for the intersection:

\[P(A \cap B) = P(A|B)P(B) = P(B|A)P(A)\]

If events $A$ and $B$ are independent, we can just plug in $P(A)$ for $P(A|B)$, and this reduces to:

\[P(A \cap B) = P(A)P(B)\]

It’s clear, then, why it’s pretty convenient to have independent events: it means that you can just multiply marginal probabilities to get probabilities of intersections (if you want the probability of $A$ an $B$ occurring and $A$ is independent of $B$, you could just multiply $P(A)$ by $P(B)$). This is pretty useful, but, of course, you have to be careful: you must prove that events are independent before you multiply the marginal probabilities. In fact, this is one of the most common probabilistic fallacies: multiplying the marginal probabilities of events to find the probability of the intersection (and, in truth, a mistake you may have made when working with probabilities in the past). Often, events are positively correlated, meaning that conditional on one event occurring, another is more likely (we will discuss this concept much more in depth in Chapter 7). This makes the probability of the intersection much higher than the simple product of all of the marginal probabilities!

A quick note: independent events are different from disjoint events. Remember, disjoint events are events without overlap. That is, for disjoint events $A$ an $B$:

\[P(A \cap B) = 0\]

This actually means that $A$ and $B$ are dependent; if we know that $A$ occurs, then we know that $B$ cannot occur, since there is no intersection!

Let’s explore independence further with a simulation in R. Imagine that we flip a fair coin and roll a fair die each ‘round.’ Let $H$ be the event that we get ‘heads’ on the coin, $E$ be the event that we get an even roll on the die and $O$ be the event that we get the odd roll on the die. Based on what we’ve just discussed, we can easily see that $H$ is independent of $E$ and $O$: knowing that the coin is heads gives no information about the die roll! However, $E$ and $O$ are highly dependent: if we know that $E$ occurs, then $O$ cannot occur (if we have an even number, we know it’s not odd). We’ll conduct a simulation by creating ‘binary vectors’ that code the value 0 when an event does not occur and a 1 when an event does occur (which is useful here because, as we have seen, we can take the mean of the vector to find the empirical probability). Then, we will examine the independence/dependence between the random variables.

#replicate
set.seed(110)
sims = 1000

#keep track if these events occurred or not
H = rep(0, sims)
E = rep(0, sims)
O = rep(0, sims)

#run the loop
for(i in 1:sims){
  
  #flip to see if we get heads
  flip = runif(1)
  
  #roll the die
  roll = sample(1:6, 1)
  
  #see if we got heads
  if(flip <= 1/2){
    H[i] = 1
  }
  
  #see if we got an even number
  if(roll%%2 == 0){
    E[i] = 1
  }
  
  #see if we got an odd number
  if(roll%%2 == 1){
    O[i] = 1
  }
}

#should get 1/2 for all
mean(E); mean(O); mean(H)

## [1] 0.513

## [1] 0.487

## [1] 0.521

#the probability of heads doesn't change if we condition on O and E,
#   and vice versa: they are independent!
mean(H[O == 1]); mean(H[E == 1])

## [1] 0.5051335

## [1] 0.5360624

mean(O[H == 1]); mean(E[H == 1])

## [1] 0.4721689

## [1] 0.5278311

#however, the mean of E changes when O is 1; they are dependent!
mean(E[O == 1])

## [1] 0

Let’s take this concept a step further: we can generalize this idea of independence to the concept of Conditional Independence. Events $A$ and $B$ are conditionally independent given $C$ if:

\[P(A \cap B | C) = P(A|C)P(B|C)\]

Just imagine that we are living in a world where $C$ occurred (conditioning on $C$) and $A$ and $B$ are independent in this world. An important note is that conditional independence does not imply regular independence, and vice versa. Let’s imagine an example.

You roll two fair die, one white and one red. Intuitively, the results of the two rolls are independent. Knowing that the white die is a 6 does not change the probabilities of the outcomes of the red die; they are both fair, after all! However, if we condition on the fact that the total between the two dies was 7, then the two die rolls are no longer independent. If I tell you now that the white die shows 4, then you know with certainty that the red die shows 3. In this case, the two are marginally independent, but conditionally dependent when we condition on the extra variable (the sum of the two die rolls). We can confirm this thought experiment with a simulation in R.

#replicate
set.seed(110)
sims = 1000

#generate the random variables
white = sample(1:6, sims, replace = TRUE)
red = sample(1:6, sims, replace = TRUE)


#calculate the sum of the rolls
S = white + red

#compare the distribution of white overall compared to white when red is 3
#   they should both be uniform

#set graphics
par(mfrow = c(1,2))

#graphics
hist(white, main = "White", xlab = "Roll",
     freq = FALSE,
     col = rgb(1, 0, 0, 1/4))
hist(white[red == 3], main = "White | Red = 3", xlab = "Roll",
     freq = FALSE,
     col = rgb(0, 1, 0, 1/4))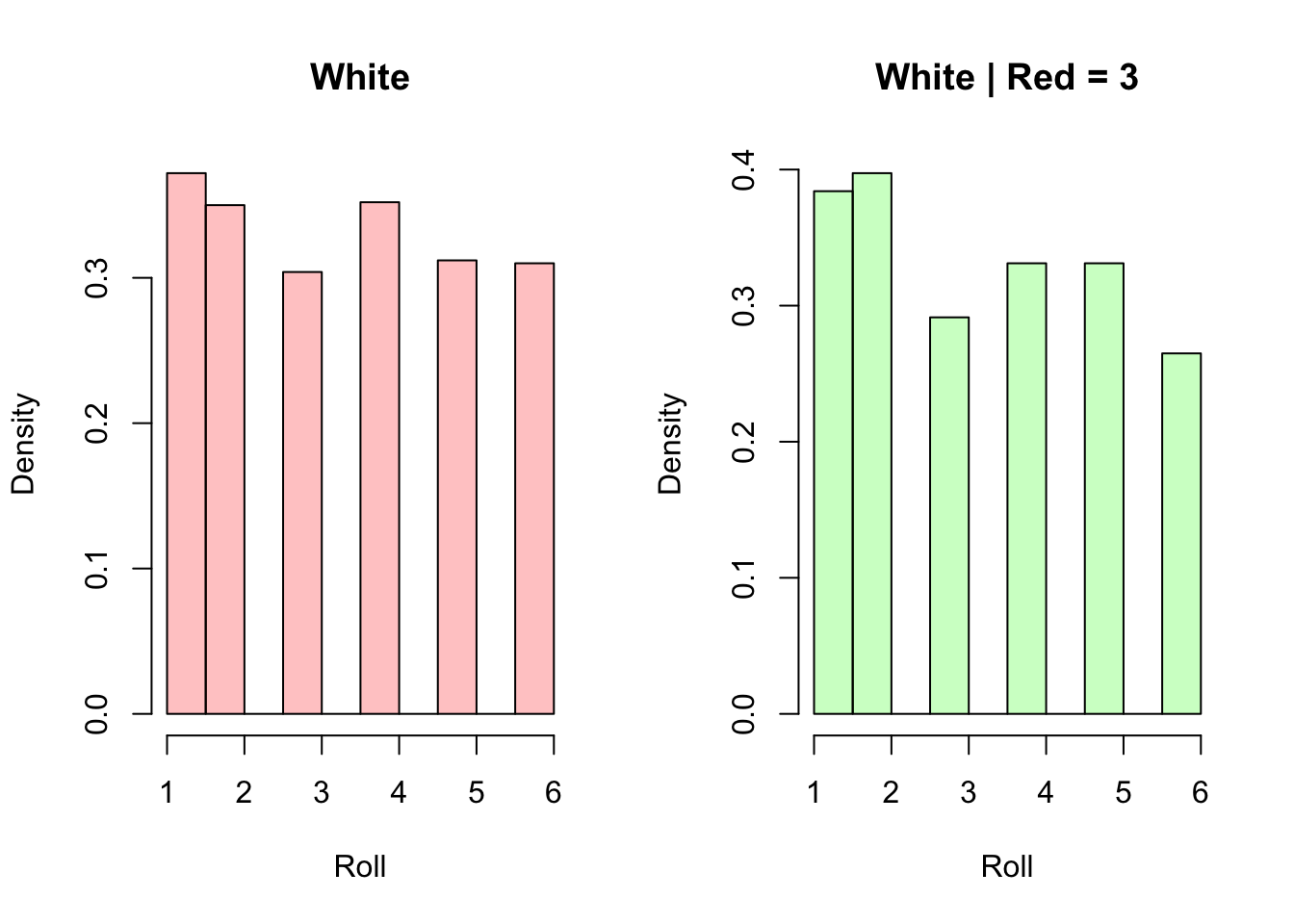

#re-set graphics
par(mfrow = c(1,1))


#now compare when we also condition on the sum being 6
#   now, we only have one option for the white roll

#set graphics
par(mfrow = c(1,2))

#graphics
hist(white, main = "White", xlab = "Roll",
     freq = FALSE,
     col = rgb(1, 0, 0, 1/4))
hist(white[red == 3 & S == 6], main = "White | Red = 3, Sum = 6", xlab = "Roll",
     freq = FALSE, breaks = 1:6,
     col = rgb(0, 1, 0, 1/4))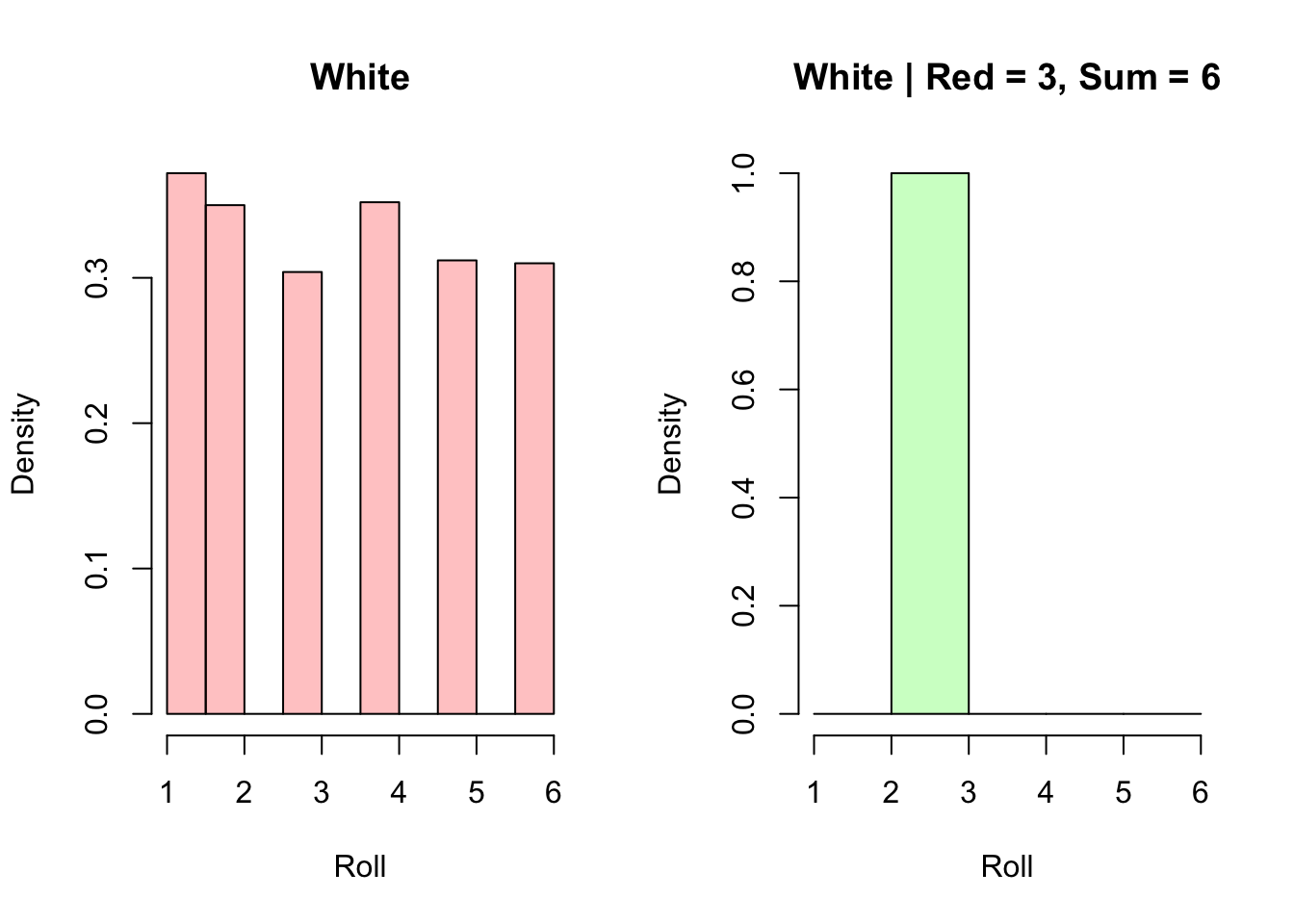

#re-set graphics
par(mfrow = c(1,1))

The Birthday Problem

Now that we have a better handle on Conditional Probability, we’ll discuss with a classic problem in Statistics: The Birthday Problem.

In case you have not heard this before, we will start with the problem statement. Consider a room of $n$ people. Imagine that their birthdays are randomly distributed among the 365 days of the year (for the sake of simplicity, assume that it is not a leap year); that is, there is a 1/365 probability of a random person being born on April 2nd, a 1/365 probability of a random person being born on May 5th, etc. Define a match as a day that more than one person has a birthday. Note that a match can occur across years; that is, January 1st, 1950 and January 1st, 1999 constitute a match (we are only interested in days of the year, not the actual year). Also note that we may have more than two people born on a specific day (i.e., 3 people on January 1st) and this still counts as a match.

This problem is concerned with finding the probability of at least one match, in terms of the number of people $n$. Specifically, the fame of this problem arises from the question “how large does $n$ have to be before we have a greater than .5 probability of getting at least one match?” Usually, the first time you see this problem, you guess somewhere around 175, because it is around half of 365 (half of the people means a .5 probability, right?). Consider the following graph that plots the actual probabilities for different values of $n$.

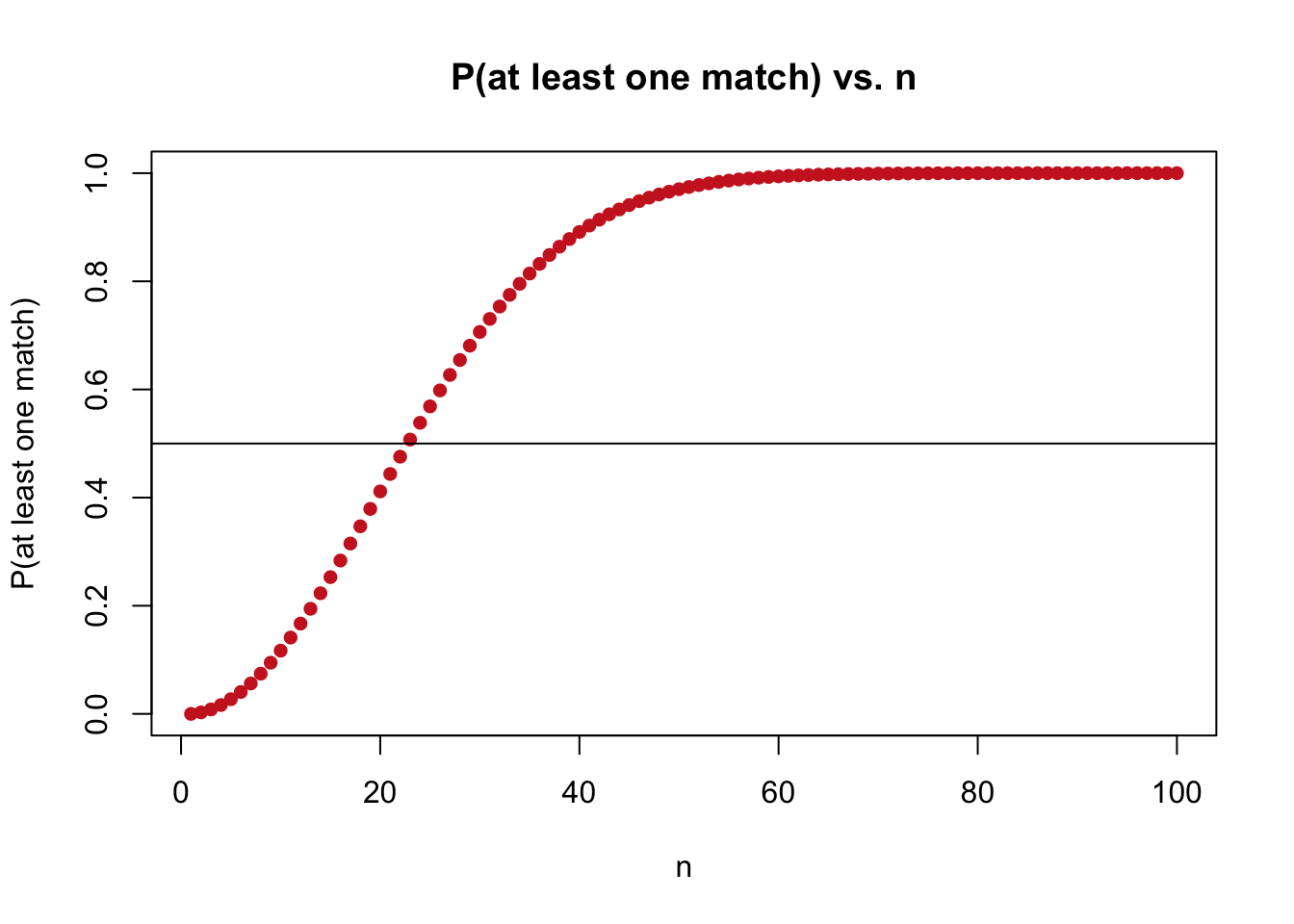
Notice that the x-axis, which counts the number of people, only runs from 0 to 100, yet the probability increases dramatically (at around 60 people, it’s almost a certainty that we get at least one match; of course, the probability only truly hits 1 when there are 366 people and it is impossible to put the people down without getting a match because there are more people than days). Astonishingly, the .5 threshold for probability (horizontal black line) is crossed at 23 people! That means, if we have 23 people in a room, the probability is over .5 that there is at least one match.

How could it be that, among all 365 days, such a small number of people lead to such high probabilities of matches? It simply doesn’t seem possible that 23 people cover enough of the 365 days to make the probability so high. You could try this for yourself in a large group, or we could solve this problem using the probability skills we have developed so far.

We’ll start by trying to solve analytically for the probability of ‘at least one match’ for a general value of $n$. Consider for a moment solving this probability directly. This problem could get very tricky, very quickly. We could have 2 people being born on the same day, 3 people born on the same day, all the way up to $n$ people; each of these constitutes as having ‘at least one match.’ In addition, we have to consider that any combination of the $n$ people could make up these matches. We also would have to consider that there could be multiple ‘match days’: perhaps there are two days that both have 2 people born on them!

Instead, it will be easier here to use the complement (usually, whenever you need the probability of ‘at least’ something, the complement is useful). Recall this concept introduced in the Chapter 1: if $A$ is an event (or ‘set’), then $A$ complement (often denoted $A^c$ or $\bar{A}$) is the event ‘$A$ doesn’t occur.’ Here, letting $A$ be the event that at least one match occurs, we know:

\[P(A) = 1 - P(A^c)\]

Remember, in our notation, $P(A)$ means in english ‘the probability that $A$ occurs.’ Anyways, in this case, it will be a lot easier to find $P(A^c)$ than $P(A)$. In words, this is finding the probability of no matches among all $n$ people.

For there to be no matches among $n$ people, we need each person to have a unique birthday. That is, the first person must have a birthday that is different from all of the other birthdays in the sample. Consider now iterating through each person, and putting them down on the calendar one by one. The first person has 365/365 probability of getting a unique birthday: there are 365 possible days, and all of them are unique (so far, since no one else has been put down yet). Now consider the second person. They have a 364/365 probability of getting a unique birthday: there are 365 possible days, and all but one of them (the birthday of the first person, who we have already ‘put down’ on the calendar) are unique.

Imagine the simple case when $n = 2$ (we have two people). To find the probability of no match, $P(A^c)$, we would multiply the two above numbers:

\[P(A^c) = \frac{365 \cdot 364}{365^2}\]

Why did we multiply? Recall from earlier that $P(B|A) = \frac{P(A \cap B)}{P(A)}$, which implies $P(A \cap B) = P(B|A)P(A)$ (the left hand side means ‘the probability that $A$ and $B$ occur, the right side is the probability that $A$ occurs times the probability that $B$ occurs given that $A$ occurred). Now imagine that we let $A_1$ be the event that the first person has a unique birthday and $A_2$ be the event that the second person has a unique birthday. In the two person case, $P(A^c) = P(A_1 \cap A_2)$. That is, the probability of no match is the probability that both the first two people have unique birthdays. By the formula above, this can be written as $P(A_1 \cap A_2) = P(A_1)P(A_2|A_1)$. We found $P(A_1)$ with the 365/365 argument in a previous paragraph. For $P(A_2|A_1)$, recall that we are ’putting people down’ one by one, so we put person 2 down after person 1; this means that we are essentially conditioning on the first person having a unique birthday. Therefore, $P(A_2|A_1) = 364/365$, as we found above (based on the first person having a unique birthday/being on the calendar, there are 364 unique days left for the second person). For even more intuition, consider how we can cancel a 365 in the numerator and denominator above and be left with $364/365$. Again, this means that it doesn’t matter where the first person ends up, only that the second person doesn’t match the first person’s birthday.

Now imagine that we have the case with general $n$, not just $n = 2$. This multiplication pattern continues (the notation for the conditional probabilities changes and grows more complex, but the principle behind it is the same). If we extend this to the general case, we get:

\[P(A) = 1 - P(A^c) = 1 - \frac{365 \cdot 364 \cdot ... \cdot (365 - n + 1)}{365^n}\]

Of course, we could cancel the 365 term like we just mentioned, but leaving it in gives us more intuition (it’s easier to remember how we got to the result; that is, the ‘story’ behind it).

Remember, we just achieved this result by putting the first person down and seeing the probability of a unique birthday, then the second person, then the third (if the first two birthdays are unique) etc. Just imagine putting people down 1 by 1, with the probability of a unique birthday decreasing slightly every time (since if the people before them all have unique birthdays, each person takes away 1 day of the year). This result, which is a function of $n$, increases quickly, as evidenced by the fact that $n = 23$ yields a probability over .5. For intuition on this surprising result, consider this: 23 people seems much smaller than the 365 days, but there are ${23 \choose 2} = 253$ pairs of people; this certainly seems to take up more of the 365 days in the calendar than the 23 individual people!

We can confirm our intuitions with some code in R that compares the analytical result to an empirical simulation. For the empirical simulation, we will iterate over different values of $n$ (10 to 50), running a loop for each value of $n$ that generates random birthdays and keeps track of how many times we get at least one match. For the analytical solution, we define a function based on our result above (we could also use the pbirthday() function, which is built into R and is designed to calculate these probabilities). The results match in the below plot, which confirms our intuition.

#replicate
set.seed(110)
sims = 1000

#define a function to calculate the analytical result
match.prob <- function(n){
  
  #define the vector in the numerator
  v = 365:(365 - n + 1)
  
  #return the correct probability
  return(1 - prod(v)/365^n)
}

#run from 10 to 50 people
people = 10:50

#keep track of the match probability
p.match = rep(NA, length(people))

#iterate over the people
for(j in 1:length(people)){
  
  #keep track of matches
  matches = rep(0, sims)
  
  #run the inner loop (actually generate birthdays)
  for(i in 1:sims){
    
    #generate the birthdays
    bdays = sample(1:365, people[j], replace = TRUE)
    
    #see if we got a match (i.e., less unique bdays than people)
    if(length(unique(bdays)) < people[j]){
      matches[i] = 1
    }
  }
  
  #track the mean
  p.match[j] = mean(matches)
}

#compare the plots
plot(1:100, sapply(1:100, function(x) match.prob(x)),
     main = "P(at least one match) vs. n",
     xlab = "n", ylab = "P(at least one match)",
     col = "firebrick3", type = "l",
     lwd = 4)
abline(h = 1/2, col = "black")

#plot the empirical result
lines(people, p.match, col = "dodgerblue4",
      lwd = 4, type = "p", pch = 16)

#add a legend
legend("bottomright", legend = c("Empirical Result", "Analytical Result"),
       lty=c(2,1), lwd=c(2.5,2.5),
       col=c("dodgerblue4", "firebrick3"))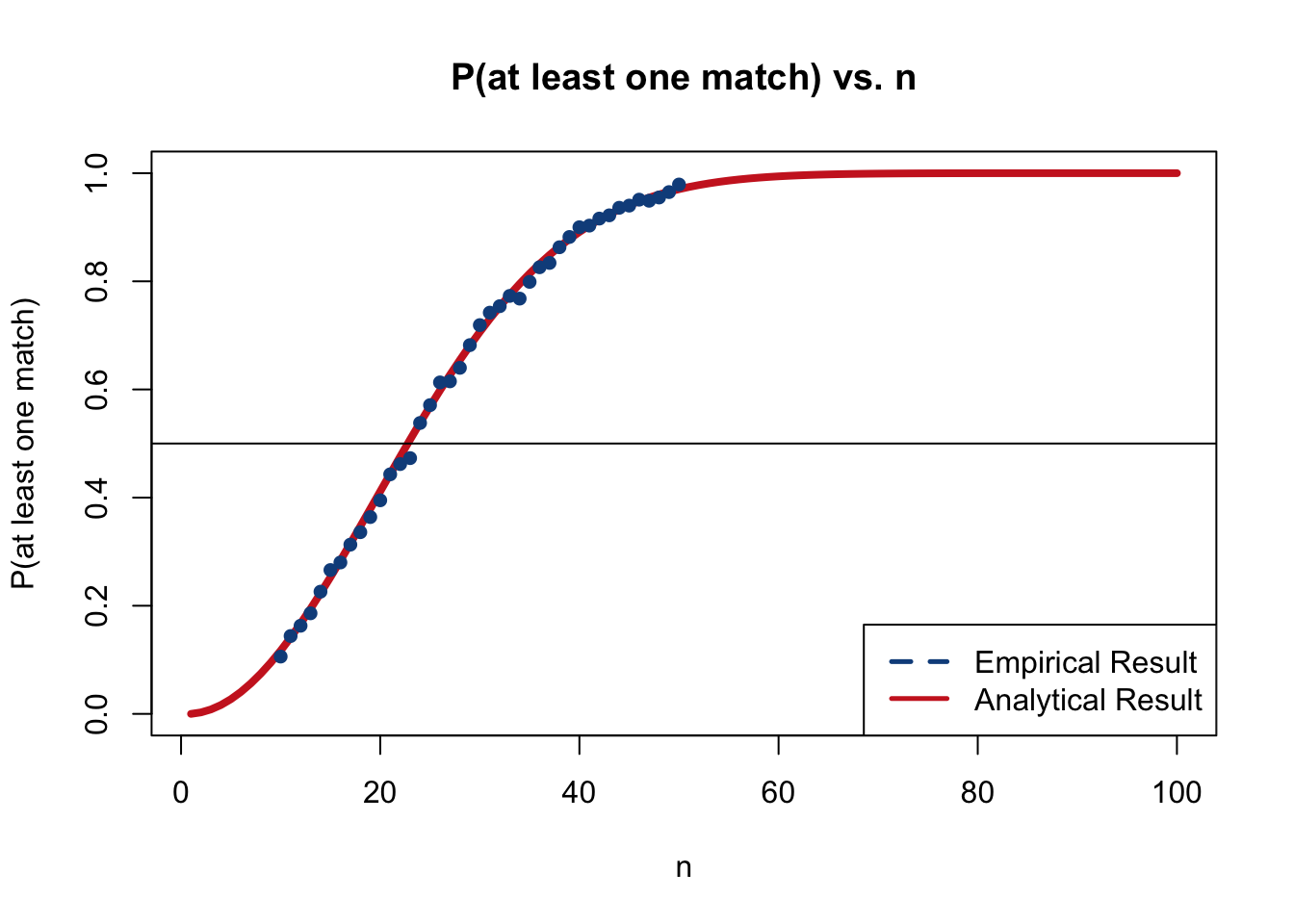

If you are still skeptical of this result, the best way to explore the idea more is to actually try it yourself. Because you probably don’t have a limitless supply of large, random crowds of people at your disposal, we built a Shiny app instead. Reference this tutorial video for more.

Click here to watch this video in your browser. As always, you can download the code for these applications here.

Monty Hall

It would be irresponsible to write a probability textbook without including the Monty Hall problem. You’ve likely heard of this infamous example before. Marilyn vos Savant discussed this question in her column, calling it the “Game Show Problem.” She gave the correct response to the question; however, the solution is so un-intuitive that scholars throughout the country vehemently disagreed with her conclusion (and let her know with some nasty fan mail). It wasn’t until people actually ‘simulated’ the problem by playing the game themselves that they agreed Marilyn was right (note the power of simulation; if you are unsure of an answer, you can always simulate it).

The problem statement is as follows. You are on a game show, where Mr. Monty Hall is the host. There are three closed doors. A car has been placed behind one of the doors at random; there are goats behind the other two doors (assume that you prefer the car to the goat). You pick a door; say, for the purpose of this example, you pick Door 1. Monty, who knows where the car is, then opens up Door 2 to reveal a goat (importantly, Monty will always open a door with a goat, and if you pick the door with the car so that the other two doors have goats behind them, he will select one of the goat doors to open with equal probabilities). He then offers you the option to stay with Door 1 or switch to Door 3. Should you switch doors?

Most people would automatically guess that the probability of winning if you stay is the same as the probability of winning if you switch (1/2, since there is one door left with the car and one with the goat). However, like Marilyn correctly answered, there is actually now a 2/3 probability that the car is behind Door 3, and thus you should switch.

This is certainly an un-intuitive result. However, it’s fairly straightforward to think about in terms of Bayes’ Rule and conditional probability. Assume that you pick Door 1 (it doesn’t matter what door you pick, but specifying the door helps us to visualize the problem). Let’s define some events. Let $C$ be the event that the car is behind Door 1. Let $G$ be the event that Monty opens Door 2 (remember, Monty will always open a ‘goat’ door, so if Monty opens Door 2 he will be revealing a goat; that’s why we name this event $G$). We are interested in $P(C|G)$, or the probability that the car is behind Door 1 (which we picked) given that Monty opened Door 2. By Bayes’ Rule:

\[P(C|G) = \frac{P(G|C)P(C)}{P(G)}\]

Let’s consider each of the probabilities on the RHS. $P(C)$ is simply $1/3$, since marginally the car is equally likely to be behind any of the 3 doors, so by symmetry it has probability $1/3$ of being behind Door 1. $P(G)$ is $1/2$; remember, we are always going to select Door 1, which means Monty can open Door 2 or Door 3, and by symmetry they both have equal probability. Finally, consider $P(G|C)$, or the probability that Monty opens Door 2 given that the car is behind Door 1. If the car is behind Door 1, that means there are goats behind Doors 2 and 3, and the problem specifies that if Monty has a choice of what door to open he picks a door to open with equal probabilities. So, $P(G|C) = 1/2$, and putting it all together yields:

\[P(C|G) = \frac{\frac{1}{2} \cdot \frac{1}{3}}{\frac{1}{2}} = \frac{1}{3}\]

So, the probability that the car is behind Door 1, conditioned on Monty opening Door 2, is $1/3$, which means the probability that the car is behind Door 3 is $2/3$ (since the car must either be behind Door 1 or Door 3 if Monty opens Door 2 to reveal a goat).

We can confirm this result with a simulation in R. In this simulation, we will again assume that we always select Door 1 (this does not change the problem, it simply makes it easier to visualize and code). We place the car randomly behind a door each time, and then generate which door Monty opens based on the context of the problem (i.e., if there is a goat behind Door 1, then Monty must open the other goat door, and if the car is behind Door 1, then Monty opens Door 2 or Door 3 with equal probabilities).

#replicate
set.seed(110)
sims = 1000

#door that monty opens
monty = rep(NA, sims)

#keep track of where the car is
car = rep(NA, sims)

#run the loop
for(i in 1:sims){
  
  #generate the doors randomly; 1 is the car, 0 is a goat
  doors = sample(c(1, 0, 0))

  #mark where the car is
  car[i] = which(doors == 1)
  
  #if we picked the car, monty opens another door at random
  if(car[i] == 1){
    monty[i] = sample(c(2, 3), 1)
  }
  
  #if we picked a goat, monty opens the other goat door
  if(car[i] != 1){
    
    #label the picked door; always pick door 1
    doors[1] = 1
    
    #monty picks the other goat
    monty[i] = which(doors == 0)
  }
}

#probability that the car is behind door 1 or door 3
#   should be 1/3 and 2/3, respectively
length(car[car == 1 & monty == 2])/length(car[monty == 2])

## [1] 0.326087

length(car[car == 3 & monty == 2])/length(car[monty == 2])

## [1] 0.673913

You can read more about the Monty Hall problem (as well as some interesting expansions and variants) in Rosenthal (2008). This article also serves to build some intuition about the seemingly strange result of this problem.

Gambler’s Ruin

Before we dive into Random Variables (which are, probably, the most significant concept in this book) let’s discuss an interesting and exciting probability problem: Gambler’s Ruin. Even the name is dramatic and exciting!

Let’s start with the problem prompt. You have two gamblers, named $A$ and $B$, such that $A$ starts with $i$ dollars and $B$ starts with $N - i$ dollars (so that there are $N$ total dollars in the game, since if you add together the gamblers’ purses you get $i + N - i = N$). They play repeated ‘rounds’; for each round, player $A$ has probability $p$ of winning the round, and player $B$ has probability $q = 1 - p$ of winning. The rounds are independent (i.e., the outcome of a previous round does not affect the outcome of the current round). If $A$ wins a round, $B$ gives a dollar to $A$; if $B$ wins a round, $A$ gives a dollar to $B$. They play until one player is out of money (has 0 dollars, so that the winning player has all of the money, or $N$ dollars).

Consider tracking the amount that $A$ has throughout the game. This value oscillates between 0 and $N$, each step moving up one with probability $p$ and moving down one with probability $q$, until hitting 0 or $N$ (i.e., $A$ goes bankrupt or wins all of the money in the game). This process is called a random walk (aptly named) and is a simple example of a ‘stochastic process,’ or a random variable that evolves through time (we’ll see more stochastic processes when we study Markov Chains in Chapter 10).

A couple of interesting questions arise when we consider this type of random walk. For example, one might ask how long the average game takes, or how much variance there is in game length. Perhaps the most enticing question is “what is the probability that player $A$ wins?”

Here, we will deal with the final question (the probability that $A$ wins). We could solve this with a difference equation (i.e., we condition on one round of the game and then solve the resulting equation). However, this type of solution is a bit outside of this book’s mathematical purview. Instead, we will just report the solution here.

Let $P(A)$ be the probability that player $A$ wins. If we have $p \neq 1/2$ (that is, the probability that $A$ wins each round is not $1/2$) then:

\[P(A) = \frac{1 - (\frac{q}{p})^i}{1 - (\frac{q}{p})^N}\]

And, if we have $p = 1/2$ (the probability that $A$ wins each round is $1/2$) then:

\[P(A) = \frac{i}{N}\]

Recall that $i$ is the amount of money that player $A$ starts with, and $N$ is the total money in the game.

Let’s think about this result for a moment. The second case, where $p = 1/2$, is very intuitive; when we increase the value of $i$ (the amount that player $A$ starts with) the probability of player $A$ winning increases. When we increase $N$ (the total amount of money in the game) and keep $i$ fixed, the probability of player $A$ winning decreases; this is intuitive because increasing $N$ and keeping $i$ fixed is the same as giving player $B$ extra money! In the simple case when $i = N/2$, the probability that $A$ wins is $1/2$, which makes sense because the game is perfectly symmetric.

The first case, where $p \neq 1/2$, is a bit trickier to intuit, just because the result is less simple to look at. We can plot how the probability of $A$ winning changes as we adjust the levels of $i$, $N$ and $p$ (the three parameters) in the $p \neq 1/2$ case.

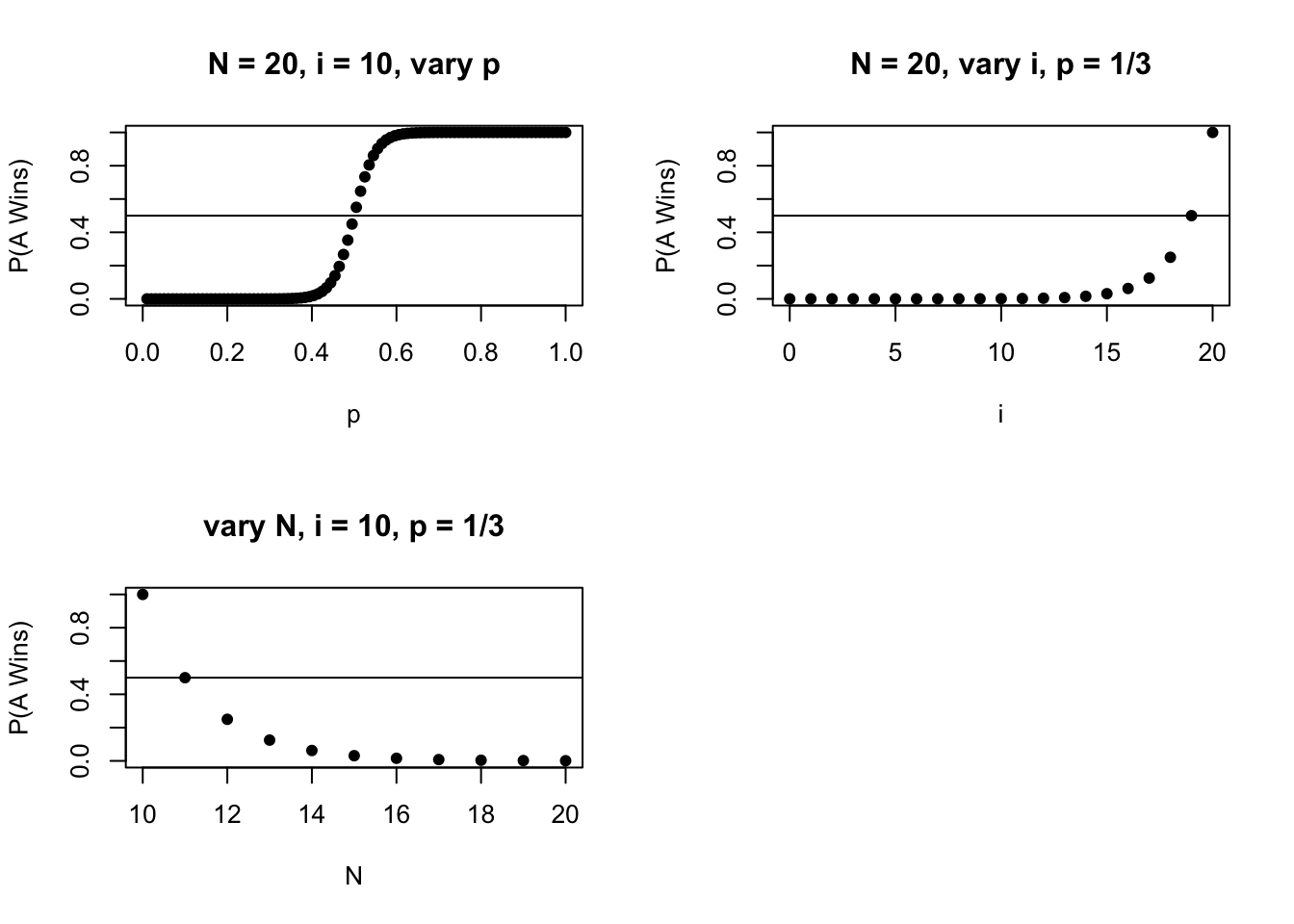
The results are intuitive: as $p$ and $i$ increase (i.e., the probability that $A$ wins each round and the money that $A$ starts with) $P(A)$ increases, and as $N$ increases while $i$ stays fixed (the money that $B$ starts with increases) $P(A)$ decreases.

Finally, one more interesting result about the Gambler’s Ruin (which we won’t fully solve here) is that you can solve for the probability that gambler $B$ wins, and this probability, plus the probability that $A$ wins, is 1. That is, there is probability 1 that someone wins, meaning that the game will end; we are certain that it won’t continue forever (Blitzstein and Hwang (2014)). This may sound obvious, but it is not necessarily a given when we are working with random walks and, by extension, stochastic processes.

You can further explore the Gambler’s Ruin problem with our Shiny app; reference the tutorial video for more.

Click here to watch this video in your browser. As always, you can download the code for these applications here.

For our purposes, it is important to understand the set-up of the Gambler’s Ruin problem, as well as the result (the probability that $A$ wins for $p = 1/2$ and $p \neq 1/2$). It is less important to understand the actual steps in the solution; i.e., solving the ‘difference equation’ to get the stated result. For example, consider the problem presented in this video:

Click here to watch this video in your browser.

Essentially, as mentioned in this video, we want to be able to recognize when we can use the set-up and result of Gambler’s Ruin to solve problems.

Introduction to Random Variables

Random variables and their distributions are probably the most important concept in this book. We’ve learned how probabilistic events are just events with uncertainty about their potential outcomes, unlike deterministic events where we are certain of the outcome (for example, $2 + 2$ is deterministic. It’s 4, every time! However, we need $P(A)$ to tell us the probability that $A$ occurs, because $A$ is not a sure thing). When you flip a coin, a probabilistic event, you aren’t sure which way it will land: there is some chance that it shows up tails, and some chance it shows up heads. We can apply this concept of uncertainty to understanding random variables.

Perhaps the best way to start thinking about a random variable is as a sort of machine that randomly spits out numbers (yes, we will define this much more rigorously in Chapter 3, but this is a good place to start the discussion for intuition’s sake). Compare this to some function $f(x)$; specifically, say you have a function $f(x) = 2x$. The behavior of the output of this function is very well defined and completely certain (or deterministic, as mentioned above): whatever you plug in, you get twice that value back (plug in $5$, get $10$, etc.). Unlike a function, the output of a random variable has uncertainty; we’re never as sure as we are with the function (although the output follows some distribution, or structured pattern, which we will get to later). It’s essentially a machine that spits out random outputs, but often with certain specific characteristics.

We generally denote random variables with capital letters, and usually we use $X$. So, we know that if you have some random variable $X$, it acts like a random function that spits out numbers (one example of such a ‘machine’ is an experiment that flips a coin 10 times and counts the number of heads).

Properties of Random Variables

As we begin to make the definition of random variables rigorous, let’s start with discussing different properties of random variables; these will help you to more fully understand the structure of these ‘machines’ that ‘spit out random numbers.’

Concept 2.5 (Distribution):

This is essentially the name of the machine or ‘type’ of the random variable. A distribution describes the ‘pattern’ that the random variable follows. Imagine a ‘recipe,’ (the distribution) that gives the instructions to make a specific ‘meal’ (the random variable). We will be covering plenty of different distributions in this book, as you can likely see by scrolling through the table of contents on the left side of the page.

So, we call a random variable a ‘Binomial random variable’ if it has a Binomial distribution, much like we call a ‘hamburger’ a meal that came from a recipe for hamburgers. Each distribution has it’s own properties (expectation, variance, probability mass function, etc.), just like menus have ingredients, different cooking tools, etc. This ‘menu’ analogy will come in handy when we consider the distinction between a random variable and its distribution.

Concept 2.6 (Expectation):

A random variable’s expectation is another name for its average, and it is denoted by $E(X)$ (which means, in english, ‘the expectation of random variable $X$’). The expectation of the number of heads in one coin flip (which is a random variable) is $.5$ (we will formalize why this is true later, but for now just use your intuition: there is a 50/50 chance of the outcomes 0 and 1). Note that the expectation might not necessarily be a value that the random variable can possibly take on; we can’t actually flip .5 heads, it’s just the numeric average of all of the probabilistic outcomes. Just like averages are incredibly useful for summarizing data, expectation is a key part of surmising a specific random variable (a central piece in the ‘menu’).

Concept 2.7 (Variance):

As the name overtly suggests, this describes how much spread is inherent in a certain random variable, and is notated $Var(X)$ (in english, ‘the variance of the random variable $X$’). Without first even considering how to calculate variance, it is probably reasonable to think about it in relative terms: if you were counting the number of heads, you would expect higher variance in the number of heads from flipping a coin 10 times than just flipping it 5 times, for example.

Concept 2.8 (PMFs and CDFs):

Random variables have probability mass functions, or PMFs (for discrete random variables), and probability density functions, or PDFs (for continuous random variables). For the moment, we will only focus on the former: the PMF gives the probability that the random variable takes on a certain value. Usually this is denoted $P(X=x)$, where $x$ represents the value that the random variable $X$ takes on (it’s very important to remember that $X$ is a random variable and $x$ is the specific, known constant that $X$ ‘crystallizes’ to). So, if we were flipping a coin 10 times, you could use the probability mass function to find $P(X=3)$. In this case, you would just plug $3$ into the function (we’ll learn more about the specific functions when we get into specific random variables: for now, just imagine plugging it into something like $x/15 + 1/10$. This specific function would tell us that $P(X = 3) = 3/15 + 1/10 = .3$).

A step further than the PMF is the cumulative density function (which is the same for continuous and discrete variables; both have CDFs, there is no CMF!). This gives $P(X \leq x)$, or the probability that a random variable takes on the value $x$ or less. We saw that if we plugged 3 into the PMF of a random variable, we would get the probability that the random variable takes on 3 (in the example of flipping a coin 10 times and measuring the number of heads, this would be the probability that you flip exactly 3 heads). If you plug 3 into the cumulative distribution function, or CDF, then you get the probability that you flip three heads or less (so 0, 1, 2 or 3 heads). The notation for a CDF is $F(x)$ with a capital $F$, where $X$ is the random variable. Therefore, $F(4)$ gives the probability that the random variable $X$ takes on a value 4 or less (in both the discrete and continuous cases). Perhaps not surprisingly, the CDF is the sum of the PMF up to a specific point. They also have a few special properties: they are increasing functions, right-continuous (when you approach from the right, they are continuous), approach 0 as $x$ approaches $-\infty$ (makes sense, nothing is smaller than negative infinity) and 1 as $x$ approaches $\infty$ (also makes sense, everything is smaller than infinity, so as you get to infinity, 100$\%$ of your random variable output is accounted for, since it is all less than infinity).

Concept 2.9 (Support):

The support of a distribution is simply the set of possible values that the random variable can take on. For example, if you had a random variable that could only spit out negative numbers or 0, then the support would be negative infinity to 0. Supports seem trivial, but they are often very useful and important in fundamentally understanding a distribution. In the coin example before (flipping 10 coins and counting the number of heads), the support is the integers 0 to 10: we can get 0 heads, 1 heads, all the way up to 10 heads (but no other numbers of heads are possible).

Example 2.1 (Calculating Expectation and Variance):

Before we go any further, let’s ground what we’ve learned by exploring two of the properties - expectation and variance - in a brute force example. We are going to learn much more in later chapters about both of these properties (including ways to calculate them). For now, though, let’s review the basic formula to calculate expectation and variance that you might see in an introductory Statistics class. Again, we will formalize and discuss these types of calculations later, this is just to develop some intuition. First, the general formula for expectation:

\[E(X) = \sum\limits_{i} x_iP(X=x_i)\]

So, the expectation of random variable $X$ equals the sum of all the values in the support $x_i$ times the probability that each value occurs (again, this is a very important equation in Statistics that will be covered extensively later on). The best way to think of this is as a weighted average, where each value/outcome $x_i$ is weighted by the probability that it occurs. If you think back to the simple coin flipping example (random variable that counts the number of heads in 1 flip of a fair coin) this equation makes sense: $X$, or the random number of heads, takes on the value 1 with probability $.5$ (that is, $P(X = 1) = .5$), since this is just the probability of flipping a heads. It’s the same with $P(X = 0)$, so when we plug in we get $(0)(.5) + (1)(.5) = .5$, which we said before was the average number of heads in one flip of the coin. Variance has a similar looking equation:

\[Var(X) = \sum\limits_{i} (x_i - E(X))^2P(X=x_i)\]

So, the variance is the sum of the distances from the mean, squared, with all of these values weighted by the probability that each value/outcome occurs. The standard deviation is the square root of the variance.

Let’s apply these concepts, with these introductory formulas, to a basic lottery game. Say that you are rolling a fair, six-sided die. You win $\$10$ if the die roll is 5 or greater, $\$0$ if the die roll is 2, 3 or 4, and lose $\$5$ if the roll is 1.

How would you determine if this is a good game to play? It’s not immediately obvious if this is a game you would want to play (assuming that your goal is to make money). One way to find out is to calculate the expectation and variance of the game using the formulas above. For example, if the expectation is positive, then you will earn money on average. If the variance is large, though, then you could lose a lot of money (i.e., there would be big swings).

Let’s go through and calculate the expectation and variance. There are three outcomes/values that your bet can take on: $\$10$, $\$0$ and $-\$5$, all based on probabilities associated with the die: $\frac{2}{6}, \; \frac{3}{6}, \; \frac{1}{6}$, respectively. So:

\[E(X) = (10)(\frac{2}{6}) + (0)(\frac{3}{6}) - (5)(\frac{1}{6}) = 2.5\]

So the expectation of every game is $\$2.5$. Since it’s a positive value, it seems like a pretty good game to play, since on average you will win $\$2.5$ (even if there was an upfront cost of $\$1$ to play, you would still make a profit on average; in fact, you make a profit on average as long as the cost to play is under $\$2.5$). Let’s find the variance; we just found the expectation, so we can use it in the variance formula:

\[Var(X) = (10 - 2.5)^2(\frac{2}{6}) + (0 - 2.5)^2(\frac{3}{6}) - (-5-2.5)^2(\frac{1}{6}) = 31.25\]

So the variance of every game is $\$31.25$. At this point in our statistical development, it’s kind of hard to visualize what this means exactly (if it’s big or small); we can really only compare it to other variances (for some named variables, we will have a better gauge). For example, if there was another game with expectation $\$2.5$ but variance of only $\$10$, it would be a less risky game.

Let’s check our work by playing this game over and over in R, tracking our winnings and calculating the mean and variance with the mean and var functions.

#replicate
set.seed(110)
sims = 1000

#generate winnings
winnings = sample(c(10, 0, -5), sims, replace = TRUE, prob = c(2/6, 3/6, 1/6))

#the mean and variance should match above (2.5 and 31.25)
mean(winnings); var(winnings)

## [1] 2.545

## [1] 30.6286

Binomial

We’ve seen what random variables are and the properties that make each unique. Now, we will explore specific, well-defined distributions; i.e., the ‘hot-dogs,’ ‘hamburgers,’ and ‘pizzas’ (famous, well-defined recipes for food). Each one has their own structured expectation, variance, probability mass function, etc. (just like hamburgers have structured ingredients, cooking tools etc.). This is not only one of the most interesting portions of the book but one of the most applicable to real life problems, and some of the best preparation for future education in Statistics. Hopefully this section will clear things up a little bit; while we’ve discussed all of these properties, we haven’t yet seen them in action.

Specifically, we’re going to start with the Binomial Distribution. It is a discrete distribution: it takes on discrete values (like ${1,2,3}$), not continuous values (like all of the values between $1$ and $2$). That is, the support is discrete.

This wasn’t mentioned in the previous section, but we say that each distribution has a Story (terminology adapted from Professor Blitzstein). Beyond all of the math, what really makes these distributions interesting is a summary of what is actually going on in plain english; what kind of random process is occurring. The story of the Binomial is we perform $n$ independent trials, each with only two outcomes (usually we think of these two outcomes as success or failure) and with a probability of success $p$ that stays constant from trial to trial.

Sounds a little tricky, but consider flipping a fair coin $n$ times and hoping to get heads (counting heads as a ‘success’). This is the prototypical example of a Binomial random variable. It meets all of the requirements: there are a set of $n$ trials, each trial has only two outcomes (heads, which we’ll define as success here, and tails, which we’ll define as failure here), the probability of success/heads is .5 for every trial, and each flip of the coin is independent from the other flips.

How about some more examples? Remember Charlie from Charlie and the Chocolate Factory? The noble, humble child who sought out lottery-esque golden tickets in random Willy Wonka chocolate bars? If chocolate bars are independent of each other, and Charlie buys $10$ bars, where each bar has a $1\%$ chance of having a golden ticket, than the random variable $G$ that measures how many golden tickets Charlie wins has a Binomial distribution (you might argue that the probability isn’t a constant .01 for every bar, since we are sampling ‘without replacement’; once we eat many ticket-less bars, there are less ticket-less bars in the population, meaning a ticket bar is more likely on the next try. Anyways, assume that the probability is constant here! This is probably a reasonable assumption because there are so many bars that the probability change from sampling is negligible). What about a college student asking people out on dates? If prospective dates make their decisions independently, and the college student asks out 30 people, where each has a probability .2 of saying yes, than the random variable $D$ that measures how many dates he gets is Binomial.

Hopefully, then, we have a general sense of what the Binomial represents. If indeed some random variable has a Binomial distribution (remember, it’s important to realize that random variables have distributions, just like meals have recipes, and multiple random variables can have the same distribution, just like multiple meals might have the same recipe), we use the following notation:

\[X \sim Bin(n,p)\]

Where $X$ is the random variable.

The $\sim$ means, in english, “has the distribution….” So, here, the random variable $X$ has a Binomial distribution. The $n$ and $p$ are the parameters of the distribution. As you may have guessed, the $n$ represents the number of trials, while the $p$ represents the probability of success on each trial.

The parameters are very important: in addition to the specific distribution, they essentially give us all the information we need about a specific random variable, and they will soon fuel our calculations of expectation, variance and probability mass (they govern the distribution). You should get familiar with defining a Binomial distribution with these parameters given some sort of verbal set up (or ‘story’). For example, if we were running an experiment for a random variable $T$ that measures the number of tails that we get from flipping a fair coin 30 times, we could write:

\[T \sim Bin(30,.5)\]

Since 30 = $n$ = total number of trials and .5 = $p$ = probability of success on each trial.

Now that we’ve established the set-up for a Binomial, we can discuss the characteristics that make it unique: its expectation, variance, and probability mass function. For a Binomial random variable $X$, we have:

\[E(X) = np, \; Var(X) = npq\]

Where $q = 1 - p$ (this is relatively common notation in Statistics). So, the expectation of successes in a Binomial random variable is the total number of trials times the probability of success on each trial (intuitive) and Variance is the number of trials times the probability of success times the complement of the probability of success (unfortunately, not intuitive. However, it makes sense that the variance grows when $n$ grows - more trials means more variance - and is maximized when $p = 1/2$ - the farther we get from a 50/50 chance, the more ‘consistent’ the results become. Consider when $p = 1$ or $p = 0$; we have no variance, because we either have all successes or all failures with total certainty).

So, consider our previous example, $T \sim Bin(30,.5)$, where $T$ represents number of tails in 30 coin flips. We expect $30\cdot .5 = 15$ tails on average, with the variance of these tails being $30\cdot.5\cdot(1 - .5)= 7.5$ (remember, the standard deviation is always just the square root of the variance, so the standard deviation is $\sqrt{7.5}$).

Finally, then, we have the probability mass function of a Binomial (PMF). Recall that a probability mass function gives the probability that a random variable $X$ takes on any one value $x$, or $P(X=x)$ for all $x$. For a Binomial, we have:

\[P(X=x) = {n \choose x}p^x q^{n - x}\]

With our extensive knowledge of counting that we developed in Chapter 1, we are not deterred by the ${n \choose x}$ and can now break this formula down.

Let’s consider an easy example. Let $X$ be a random variable that represents the heads flipped from flipping a fair coin 5 times. We know this is Binomial (set number of trials, same probability across trials, only two outcomes on each trial, trials are independent), so we know $X \sim Bin(5,.5)$. Plugging in for $n$, $p$ and $q$ (remember, $q = 1 - p$ in this notation):

\[P(X=x) = {5 \choose x}.5^x .5^{5 - x}\]

So, this becomes a function where we plug in $x$ to find the probability of $x$ successes.

A simple example would be finding the probability that exactly 3 heads occur in the 5 flips. Plugging in 3 for $x$ (again, we interpret this as the ‘value that the random variable $X$ takes on’), we would get:

\[P(X=x) = {5 \choose 3}.5^3 .5^{5 - 3}\]

Which comes out to .3125.

Why does this PMF correctly give the desired probability? Let’s break down the components of the equation.

First, consider the ‘probability’ portions, $.5^3$ and $.5^{5-3}$. Think about what these are saying. When you get 3 heads in a row followed by 2 tails in a row, what is the probability that this sequence occurred? Remember, since each flip is independent from the other flips, we can multiply the marginal probabilities of each flip to get the probability of the intersection, or combination of flips. Therefore, the probability of 3 heads is just $.5\cdot.5\cdot.5$, or $.5^3$, and the probability of 2 tails (you must get 2 tails, since there are 5 total flips and exactly 3 are heads) is just $.5\cdot.5$, or $.5^2$ (we have it written as $.5^{5-3}$, which is the same thing, and actually is more commonly used notation).

Therefore, it turns out in this case that $.5^3 .5^2 = .5^5$ (again, we can multiply because flips are independent) gives the probability of three heads heads in a row followed by two tails in a row (you won’t usually be able to combine terms because the probability of success won’t always be $.5$ and thus the probability of success and failure won’t always be equal). However, $.5^5 = .03125$, which is not the answer our probability mass function gave us. Why is this?

What we just found is the probability of any one desirable permutation occurring (specifically, 3 heads and then 2 tails, or $HHHTT$ in this example). However, this is only one way of many desirable permutations (3 heads in 5 flips) can occur; two other examples are HHTTH and HHTHT. In this case, we want to count these different orderings. Our random variable is asking for instances when we flipped 3 heads out of 5 flips; it doesn’t care about the order in which we got them!

Of course, we know that the probability of each individual permutation is the exact same, since they all have 3 heads and 2 tails. Therefore, we merely have to multiply the probability of a desirable permutation, $.5^5$, by the number of desirable permutations that can occur (imagine that we are just summing up the probabilities of all of the favorable outcomes). How many desirable permutations are there? Well, how many ways can you get 3 heads out of 5 flips? As we learned in a previous chapter, this is exactly the concept counted by the binomial coefficient, ${n \choose x}$. In this case, ${5 \choose 3}$ gives the number of ways that you can pick 3 heads out of 5 flips (or, the number of ways to pick 3 coins out of 5 to make heads). Here, this comes out to 10 ways.

So, we multiply the probability of each desirable permutation (3 heads in 5 flips) by the total number of desirable permutations to get the overall probability that we find a desirable permutation. Here, $.03125\cdot10 = .3125$, which matches what we got from our PMF.

Remember, then, the $p^x q^{n - x}$ as the ‘probability’ part of the desirable permutation, and the ${n \choose x}$ part as the ‘number of desirable permutations.’ It’s a good exercise in counting/probability to go through the PMF and understand it, since it can often give you new insights into the story of the distribution itself.

Lastly, the support of a binomial is the integers 0 to n, inclusive. This is intuitive, since if we are flipping coins we can get 0 and any positive number up to (and including) n, but not negative numbers (and they must be integers; we can’t have 3.7 flips of a coin). Remember, even if the support consists of integers, that doesn’t mean that the expectation or variance must also be integers; the expectation does not have to be a value that the random variable actually takes on!

One of the best capabilities of R is that all of the famous distributions are included in the base package. It’s good practice to play around with some of the important functions: rbinom, dbinom, pbinom and qbinom help you generate random values, evaluate the PMF, evaluate the CDF and find quantiles, respectively. We’ll do some examples here; see the Glossary in the R Chapter for more.

#find P(X = 3), where X ~ Bin(10, 1/2)
dbinom(3, 10, 1/2)

## [1] 0.1171875

#find P(X <= 6), where X ~ Bin(15, 1/3)
pbinom(6, 15, 1/3)

## [1] 0.7969611

#find the value of x such that P(X <= x) = .9, where X ~ Bin(50, 1/5)
qbinom(.9, 50, 1/5)

## [1] 14

#generate 5 random draws from X, where X ~ Bin(30, 1/4)
rbinom(5, 30, 1/4)

## [1]  8  5 12  9  5

You can further explore the Binomial distribution with our Shiny app; reference this tutorial video for more.

Click here to watch this video in your browser. As always, you can download the code for these applications here.

So, to surmise, a Random Variable is essentially a machine that spits out random numbers. Certain ‘machines’ follow certain patterns: these are the our named distributions that we will work with. Each distribution has a ‘story’ that explains what type of ‘machine’ it is (Binomial story is essentially flipping coins), an expectation and a variance, a probability mass/density function and a cumulative density function (that give probabilities at specific points and probabilities up to a certain point) and a support. We will formalize the definition of a random variable in the next chapter.

We talked a lot about individual distributions here but, as you are probably starting to grasp, everything in Statistics is connected, and something even more important than the individual distributions are their connections. Keep an eye out for these relationships as we learn about more and more distributions.

Practice

Problems

2.1

Juan has $n = 10$ different pairs of socks ($2n$ socks total). Every morning when we wakes up, he randomly chooses socks one at a time until he gets a pair (i.e., both socks from the fifth pair). Let $X$ be the number of socks he chooses before he gets a pair (not including the sock that makes a pair). Find the PMF of $X$.

Hint: Define a ‘double factorial’ $n!!$ as a factorial that skips every other number; for even numbers the factorial iterates down to 2, and for odd numbers the factorial iterates down to 1. For example, $10!! = 10\cdot 8 \cdot 6 \cdot ... \cdot 2$ and $9!! = 9\cdot 7 \cdot 5 \cdot ... \cdot 1$. This may be useful in counting the number of ways to select socks in a way that doesn’t create a pair.

2.2

You flip a fair, two-sided coin 5 times. Let $X$ be the length of the longest streak in the 5 flips (i.e., if you flip $TTTTH$, the longest streak is the $TTTT$, so $X = 4$). Given that you flip 3 heads, find the PMF of $X$.

2.3

CJ is trick-or-treating on a street with 10 houses. He selects houses at random to visit; however, if he visits any one house a second time, he is turned away. If CJ selects 5 houses randomly (of course, he may select the same one multiple times) what is the probability that he never gets turned away?

2.4

Your friend has two six-sided dice in his pocket. One is a fair die, and thus has an equal probability of landing on each number. The other is weighted, and has the following probability distribution: $\frac{1}{6}$ probability of rolling a 1, 2 or 3, $\frac{1}{8}$ probability of rolling a 4 or 5, and a $\frac{1}{4}$ probability of rolling a 6.

He takes a die blindly and randomly from his pocket and rolls it four times: the outcomes are 6, 1, 2, 3.

Given these results, what is the probability that he is rolling the fair die?

2.5

There is a disease such that $P(D)$, the probability of contracting the disease, is $.1$ for any random person. There are two symptoms, $S_1$ and $S_2$, that always occur if someone has the disease. Overall (in general), each symptom has .2 probability of occurring in a random person. Aside from the relationship to $D$, symptoms 1 and 2 are unrelated to each other.

Find the probability that you have the disease given that you experience the first symptom.
Given that you don’t have the disease, what’s the probability that you still experience the first symptom?
Given that you experience Symptom 2, what is the probability that you also experience Symptom 1?
Discuss the dependence between $S_1$ and $S_2$.
If we observe both symptoms, what is the probability that we have the disease?

2.6

You are part of a diving competition. Each dive receives a score from 1 to 10 (integers only, so the possible scores are $1,2,...,10$), with 10 being the best. You are allowed to dive three times and take your best score; this is your overall competition score. Unfortunately, the judge is not at all qualified to be at this competition, and just assigns your scores randomly from 1 to 10. However, he won’t assign the same score twice, in case the audience catches on that he knows nothing.

Find the PMF and CDF (which you can leave as a sum) of $C$, your overall competition score. You can leave the CDF as a summation. How could you find the expectation (no need to calculate here)?

2.7

Many music fans claim that sound quality is far enhanced on vinyl (i.e., record players); however, people are often skeptical that vinyl sounds any different from more modern audio methods (i.e., digital speakers).

Freddie claims that he can reliably discern vinyl audio from digital audio. If he is right, then he will correctly identify the mode of audio, digital or vinyl, with probability .8. If he is wrong, as many would claim, then he has probability .5 of correctly identifying the mode of audio.

Freddie listens to 50 songs and tries to identify the mode of audio. Let $V$ be the event that he can reliably discern vinyl from audio. Unconditionally, assume that $P(V) = 1/2$. Let $X$ be the number of songs he correctly identifies, and then $P(V|X)$ be the updated probability that he can discern vinyl from digital after observing him identify $X$ songs correctly. How large does $X$ have to be for $P(V|X) >= .9$?

2.8

You roll a fair, six-sided die twice. Let $X$ be the sum of the two rolls. Find $P(X = 7)$ using a conditioning argument; that is, do not simply count the number of ways to roll a 7 and divide by the number of possible combinations for the two rolls.

2.9

Imagine generating a random word by sampling $3 < n < 26$ letters, with replacement (from the 26 letters in the alphabet). What is the probability that this word has no repeats; i.e., $n$ unique letters?

2.10

Ali and Bill are taking a test. For any single question, Ali has equal probabilities of answering correctly or incorrectly, and Bill also has equal probabilities of answering correctly or incorrectly. For any single question, the probability that both Ali and Bill get the question correct is .4. Given that Bill gets a question wrong, what is the probability that Ali gets it right?

2.11

Consider the birthday problem with the usual assumptions. Previously, we’ve considered a ‘match’ as a single day with multiple birthdays; here, imagine a week match, which consists of a week with multiple birthdays. Find the probability that, among $n \leq 52$ people, there are no week matches and no day matches. For what value of $n$ does this probability drop below 1/2?

You may have noticed that, by daycount conventions, the ‘52 weeks’ of the year do not go evenly into the 365 days. For this problem, assume that there are 364 days in the year, not 365, just for simplicity, so that the weeks perfectly divide up the year.

2.12

Consider the birthday problem with the usual assumptions. Define a ‘month match’ as a month with more than one birthday. Given that there is at least one ‘month match,’ find the probability that there is at least one ‘day match’ (i.e., a day where multiple people are born) among $n \leq 12$ people. Compare this probability to the ‘unconditional’ probability of at least one day match in the standard birthday problem.

For this problem, assume 360 days in a year, and that each of the 12 months has 30 days, just so we don’t have to worry about the fact that months have irregular amounts of days.

2.13

Cameron is wandering around on the alphabet (A, B, etc.). He goes ‘up’ a letter (i.e., from D to C) and ‘down’ a letter (i.e., D to E) with equal probabilities. He cannot go from A to Z, nor Z to A (i.e., the alphabet isn’t circular).

If he starts at M, what is the probability that Cameron spells “HI” before he spells “NO?” Here, we equate ‘spelling’ a word to wandering around on its letters in the correct order; i.e., if Cameron wanders on PQPQR as a part of his path, then he spelled PQPQR (among other words).

2.14

(With help from Matt Goldberg, CJ Christian, Nicholas Larus-Stone, Juan Perdomo and Dan Fulop)

Imagine the standard Monty Hall problem, but Monty does not actually know what is behind each door; he picks one of the two remaining doors at random.

You pick Door 1 (for this problem, assume that you always pick Door 1), and Monty opens Door 2 to reveal a goat. Should you switch to Door 3?

See Rosenthal (2008) for variants and intuition on this type of problem.

2.15

Brandon is a cell. He splits into 2 with probability $1/2$ and dies with probability $1/2$. His offspring do the same, independently (each splits into 2 or die with equal probabilities). Let $E$ be the probability that Brandon’s population goes extinct. Find $P(E)$.

Hint: condition on the first step.

2.16

The little hand on a standard clock moves clockwise one unit (i.e., from 5 to 6) or counter-clockwise 1 unit (i.e., 1 to 12) with equal probabilities.

Find the probability that, from its starting spot, the little hand makes it a full day forward (24 hours, clockwise) before it makes it a half day backward (12 hours, counterclockwise). It does not matter how long the little hand takes to get to these endpoints; we only care about the location of the little hand relative to its starting spot.

2.17

The ‘Prisoners with Three Hats’ riddle is a common interview question. The problem statement is as follows:

There are three prisoners in a room. Each will be independently given a red hat or a green hat to wear on their head (each has a 50/50 chance of a red or a green hat and, again, the colors that they are assigned are independent). The prisoners can see each others hats, but no prisoner can see his own hat. Each prisoner is given a chance to guess the color of his own hat (which he cannot see); they can either guess a color (red or green) or pass. If at least one prisoner correctly guesses the color of his own hat and no prisoners incorrectly guess the color of their own hat, they are free to go (‘passing’ cannot count as either a correct or incorrect guess; it is merely a pass). The prisoners are not allowed to communicate with each other in any way once in the room, and they must cast their guesses simultaneously (i.e., one prisoner cannot adapt his strategy based on another prisoner guessing). The prisoners are allowed a strategy session before where they can discuss the best approach.

Upon first hearing this riddle, it seems like the best chance the prisoners have of escaping is assigning one person to randomly guess the color of their own hat, and the other two to simply pass. This results in a 50/50 chance of success (either the person guessing gets his color, or not). However, there is a superior strategy: if a prisoner sees two hats of the same color (i.e., he sees that the other two prisoners both have red hats) he guesses the other color for his own hat. If he sees that the other two prisoners have different color hats, he passes.

Find the probability of winning with the ‘superior strategy.’
You should have arrived at a probability greater than .5 in part (a). Your friend Nick hears about this strategy and says “well, then, if I see that the other two prisoners both have green hats, then there is a greater than .5 probability that my hat is red.” Is Nick correct? Explain.

BH Problems

The problems in this section are taken from Blitzstein and Hwang (2014). The questions are reproduced here, and the analytical solutions are freely available online. Here, we will only consider empirical solutions: answers/approximations to these problems using simulations in R.

BH 2.1

A spam filter is designed by looking at commonly occurring phrases in spam. Suppose that 80$\%$ of email is spam. In 10$\%$ of the spam emails, the phrase “free money” is used, whereas this phrase is only used in 1$\%$ of non-spam emails. A new email has just arrived, which does mention “free money.” What is the probability that it is spam?

BH 2.2

A woman is pregnant with twin boys. Twins may be either identical or fraternal (nonidentical). In general, 1/3 of twins born are identical. Obviously, identical twins must be of the same sex; fraternal twins may or may not be. Assume that identical twins are equally likely to be both boys or both girls, while for fraternal twins all possibilities are equally likely. Given the above information, what is the probability that the woman’s twins are identical?

BH 2.22

A bag contains one marble which is either green or blue, with equal probabilities. A green marble is put in the bag (so there are 2 marbles now), and then a random marble is taken out. The marble taken out is green. What is the probability that the remaining marble is also green?

BH 2.26

To battle against spam, Bob installs two anti-spam programs. An email arrives, which is either legitimate (event $L$) or spam (event $L^c$), and which program $j$ marks as legitimate (event $M_j$) or marks as spam (event $M^c_j$) for $j \in \{1,2\}$. Assume that 10% of Bob’s email is legitimate and that the two programs are each “90% accurate” in the sense that $P(M_j|L) = P(M^c_j|L^c) = 9/10$. Also assume that given whether an email is spam, the two programs’ outputs are conditionally independent.

Find the probability that the email is legitimate, given that the 1st program marks it as legitimate (simplify).

Find the probability that the email is legitimate, given that both programs mark it as legitimate (simplify).

BH 2.30

A family has 3 children, creatively named $A, B,$ and $C$.

Discuss intuitively (but clearly) whether the event “$A$ is older than $B$” is independent of the event “$A$ is older than $C$.”
Find the probability that $A$ is older than $B$, given that $A$ is older than $C$.

BH 2.31

Is it possible that an event is independent of itself? If so, when is this the case?

BH 2.32

Consider four nonstandard dice (the Efron dice), whose sides are labeled as follows (the 6 sides on each die are equally likely).

A: 4, 4, 4, 4, 0, 0

B: 3, 3, 3, 3, 3, 3

C: 6, 6, 2, 2, 2, 2

D: 5, 5, 5, 1, 1, 1

These four dice are each rolled once. Let A be the result for die A, B be the result for die B, etc.

Find P(A > B), P(B > C), P(C > D), and P(D > A).
Is the event A > B independent of the event B > C? Is the event B > C independent of the event C > D? Explain.

BH 2.35

You are going to play 2 games of chess with an opponent whom you have never played against before (for the sake of this problem). Your opponent is equally likely to be a beginner, intermediate, or a master. Depending on which, your chances of winning an individual game are 90%, 50%, or 30%, respectively.

What is your probability of winning the first game?
Congratulations: you won the first game! Given this information, what is the probability that you will also win the second game (assume that, given the skill level of your opponent, the outcomes of the games are independent)?
Explain the distinction between assuming that the outcomes of the games are independent and assuming that they are conditionally independent given the opponent’s skill level. Which of these assumptions seems more reasonable, and why?

BH 2.38

Consider the following 7-door version of the Monty Hall problem. There are 7 doors, behind one of which there is a car (which you want), and behind the rest of which there are goats (which you don’t want). Initially, all possibilities are equally likely for where the car is. You choose a door. Monty Hall then opens 3 goat doors, and offers you the option of switching to any of the remaining 3 doors. Assume that Monty Hall knows which door has the car, will always open 3 goat doors and offer the option of switching, and that Monty chooses with equal probabilities from all his choices of which goat doors to open. Should you switch? What is your probability of success if you switch to one of the remaining 3 doors?

Generalize the above to a Monty Hall problem where there are $n \geq 3$ doors, of which Monty opens m goat doors, with $1 \leq m \leq n - 2$.

BH 2.39

Consider the Monty Hall problem, except that Monty enjoys opening door 2 more than he enjoys opening door 3, and if he has a choice between opening these two doors, he opens door 2 with probability $p$, where $1/2 \leq p \leq 1$.

Find the unconditional probability that the strategy of always switching succeeds (unconditional in the sense that we do not condition on which of doors 2 or 3 Monty opens).
Find the probability that the strategy of always switching succeeds, given that Monty opens door 2.
Find the probability that the strategy of always switching succeeds, given that Monty opens door 3.

BH 2.42

A fair die is rolled repeatedly, and a running total is kept (which is, at each time, the total of all the rolls up until that time). Let $p_n$ be the probability that the running total is ever exactly $n$ (assume the die will always be rolled enough times so that the running total will eventually exceed n, but it may or may not ever equal $n$).

Write down a recursive equation for $p_n$ (relating $p_n$ to earlier terms $p_k$ in a simple way). Your equation should be true for all positive integers n, so give a definition of $p_0$ and $p_k$ for $k$ < 0 so that the recursive equation is true for small values of $n$.
Find $p_7$.
Give an intuitive explanation for the fact that $p_n \rightarrow$ 1/3.5 = 2/7 as $n \rightarrow \infty$

BH 2.44

Calvin and Hobbes play a match consisting of a series of games, where Calvin has probability p of winning each game (independently). They play with a “win by two”” rule: the first player to win two games more than his opponent wins the match. Find the probability that Calvin wins the match (in terms of p), in two different ways:

by conditioning, using the law of total probability.
by interpreting the problem as a gambler’s ruin problem.

BH 3.6

Benford’s law states that in a very large variety of real-life data sets, the first digit approximately follows a particular distribution with about a 30% chance of a 1, an 18% chance of a 2, and in general \[P(D = j) = \log_{10} \left(\frac{j+1}{j}\right), \textrm{ for } j \in \{1,2,3,\dots,9\},\] where $D$ is the first digit of a randomly chosen element. Check that this is a valid PMF (using properties of logs, not with a calculator).

BH 3.21

Let $X \sim \textrm{Bin}(n,p)$ and $Y \sim \textrm{Bin}(m,p)$, independent of $X$. Show that $X-Y$ is not Binomial.

3.25

Alice flips a fair coin $n$ times and Bob flips another fair coin $n+1$ times, resulting in independent $X \sim \textrm{Bin}(n,\frac{1}{2})$ and $Y \sim \textrm{Bin}(n+1,\frac{1}{2})$.

Show that $P(X < Y) = P( n - X < n+1-Y)$.
Compute $P(X<Y)$.

Hint: Use (a) and the fact that $X$ and $Y$ are integer-valued.

BH 3.35

Players A and B take turns in answering trivia questions, starting with player A answering the first question. Each time A answers a question, she has probability $p_1$ of getting it right. Each time B plays, he has probability $p_2$ of getting it right.

If A answers $m$ questions, what is the PMF of the number of questions she gets right?
If A answers $m$ times and B answers $n$ times, what is the PMF of the total number of questions they get right (you can leave your answer as a sum)? Describe exactly when/whether this is a Binomial distribution.

BH 3.45

A new treatment for a disease is being tested, to see whether it is better than the standard treatment. The existing treatment is effective on 50% of patients. It is believed initially that there is a 2/3 chance that the new treatment is effective on 60% of patients, and a 1/3 chance that the new treatment is effective on 50% of patients. In a pilot study, the new treatment is given to 20 random patients, and is effective for 15 of them.

Given this information, what is the probability that the new treatment is better than the standard treatment?
A second study is done later, giving the new treatment to 20 new random patients. Given the results of the first study, what is the PMF for how many of the new patients the new treatment is effective on? (Letting $p$ be the answer to (a), your answer can be left in terms of $p$.)

References

Blitzstein, J. K., and J. Hwang. 2014. Introduction to Probability. Chapman & Hall/CRC Texts in Statistical Science. CRC Press. https://books.google.com/books?id=z2POBQAAQBAJ.

Rosenthal, Jeffrey S. 2008. “Monty Hall, Monty Fall, Monty Crawl.” Math Horizons 16 (1): 5–7. http://www.jstor.org/stable/25678763.