Chapter 3 Discrete Random Variables

“When you flip a coin, there is a very small but finite chance you will never ever see that coin again.” - Scott Edward Shjefte

We are currently in the process of editing Probability! and welcome your input. If you see any typos, potential edits or changes in this Chapter, please note them here.

Motivation

It’s no coincidence that the named statistical distributions provide the fundamental underpinnings in this book; they are likely the most important concepts that we will discuss. Although we will cover many different types of distributions and random variables, we will also explore what connects them: often the links between them are more interesting than the distribution by themselves (truly, no distribution is an island!).

Random Variable Recap

We introduced the concept of a random variable in the last chapter and even discussed Binomial random variables. However, we didn’t exactly ‘formalize’ the definition very much (instead, we imagined a ‘machine spitting out random numbers’). Officially, a random variable is a function that maps a sample space onto the real line. Unsurprisingly, this formal definition doesn’t provide too much clarity. Perhaps the best way to envision this is with a concrete example: rolling two dice.

We know enough about experiments to say that the sample space (i.e., the listing of all possible outcomes) of this specific experiment is $S = \{(1,1),(1,2),(1,3)...(6,5),(6,6)\}$ (there are 36 outcomes by the multiplication rule, since each die has 6 possible outcomes). Here, we can immediately define a random variable (function) that maps this sample space to the real line. One example would be $X$, where $X$ is the sum of the two die rolls. This maps our sample space $S$ to $\{2,3,4,...,12\}$ (note that it’s not necessarily a one-to-one mapping; there are multiple outcomes of the experiment that map to 7 in the sample space, for example). How about $Y$, where $Y$ is the average of the two die rolls? This maps our sample space $S$ to $\{1,1.5,...,5.5,6\}$.

Both $X$ and $Y$ are random variables because they take our sample space and map it to some real number. The randomness comes from the fact that the outcomes are, well, random; rolling two dice constitutes as a random experiment. We could think now about events related to random variables: $X = 8$ would be the event that our dice sum to 8 (maybe you rolled a 2 and a 6). $Y = 1$ means that the average of the rolls is 1 (you rolled snake eyes). Probabilities work the same way: $P(X = 12)$ just means ‘the probability the sum of the dice is 12’ (we know this has probability $\frac{1}{36}$, of course: rolling two sixes).

This is a bit more formal than our ‘random machine’ definition from earlier on. Let’s refresh other characteristics of random variables that were discussed more fully in Chapter 2. There are different ‘types’ of random variables (different ‘recipes’) that spit out random numbers in different ways: different Distributions (just like there are some recipes that make hot dogs and some recipes that make hamburgers). We’ve already seen one, the Binomial, and we’ll cover a lot more in this chapter. Again, consider the distinction between a recipe and the meal that it creates: one ‘hamburger recipe’ can make multiple hamburgers (each hamburger is from the same recipe, but they are all different hamburgers!). Remember that you can have many different random variables (counting number of heads in 10 coin flips, counting number of tails in 20 coin flips, etc.) all with a Binomial distribution.

Random variables are governed by parameters (the Binomial takes number of trials and probability of success in a trial, $n$ and $p$, as the parameters). They have Expectations (essentially the average of the random variable) and Variances (the spread of the values that a random variable spits out). We defined these in the last chapter, although we’ll talk more about them at the end of this one.

Random variables also have PDFs/PMFs, depending on if they are continuous or discrete (notated by $P(X = x)$ and $f(x)$) that give the probability (or ‘density,’ in the continuous case) of a random variable crystallizing in a specific area. They also have CDFs (notated by $F(X)$), which are increasing, right continuous functions that give the probability that a random variable takes on a value less than or equal to a certain number: $P(X \leq x)$. Unsurprisingly, CDFs approach 0 as values approach $-\infty$, and 1 as values approach $\infty$ (the probability that our random variable takes on a value smaller than $-\infty$ is 0 and the probability that it takes on a value smaller than $\infty$ is 1, because nothing is smaller than $-\infty$ or larger than $\infty$).

Now, then, let’s add to our repertoire: we are going to walk through a number of distributions, talking about their stories, their expectations, etc. Usually the most complicated parts of these distributions (in the discrete case) are the PMFs. However, these are also often the best ways to understand the nature of the distribution. So, please, for the sake of Statistics, don’t brush over an ugly PMF when you see it: read through the explanation and intuition. This extra effort will often go far in helping you to understand the fundamental structure of the distribution.

Bernoulli

Since you already are familiar with the Binomial distribution, the Bernoulli should be easy to master. It’s essentially the simplest case, or a special generalization, of a Binomial: when we only have one trial ($n = 1$ for a Binomial; think about just flipping the coin once).

The Story of the Bernoulli Distribution is what you would expect: one trial with a probability $p$ of success and probability $1-p$ of failure (recall that we often use $p$ to denote a probability). Since the only parameter of interest is the probability (it’s a given that we’ll only be doing one trial, so $n = 1$ is not even considered a parameter) you can write the distribution as $X \sim Bern(p)$, where $X$ is a Bernoulli random variable with probability of success $p$. Yes, you could write the same distribution as $Bin(1,p)$, but it’s not as elegant.

The Expectation of the Bernoulli random variable is simply $p$ (if you have a .5 chance of success, then you expect .5 successes!). This makes good sense intuitively, but it also agrees with the formal definition that we learned previously: recall that the expectation of a Binomial is simply $np$, and here $n=1$. This is actually pretty interesting and, as we’ll see later, a useful result: we’ve bridged Expectation and probability (the expectation of a Bernoulli is the probability that the success actually occurs, or $p$) which will come in handy with something called ‘Indicator random variables’ later in this chapter.

The Variance is also simple: just $p(1-p)$, since the Binomial Variance is $np(1-p)$, and again $n = 1$.

Finally, our PMF, or probability that the random variable takes on a value, is simple because it can only take on two values (1 success or 0 successes). It can be written, if $X \sim Bern(p)$, as:

\[P(X = x) = p^x(1-p)^{1-x}\]

Remember, $X$ can only take on two values, 0 or 1, which means $x$ (the value that $X$ crystallizes to) in the above equation can only be 0 or 1. That means that this PMF simplifies to $p$ when $x=1$, or the probability of having a success, and $1-p$ when $x=0$, or the probability of having a failure. This makes sense because we defined $p$ and $1-p$ as probabilities of success and failure, respectively, to begin with.

The last interesting aspect of the Bernoulli distribution, which was hinted at above, is a trait called the “Fundamental Bridge”; an extremely useful tool in probability. The idea here is that we can build a link between probability and expectation: the expected value of the Bernoulli is simply the probability that the event in question occurs, or $P(X=1) = E(X)$ (since a Bernoulli random variable takes on value 1 with probability $p$ and value 0 with probability $1-p$). This will surface when we have to deal with complicated expectation problems. We’ll see it at the end of this chapter!

Geometric

So far we’ve worked with the Binomial and the Bernoulli, which, in their simplest terms, can be thought of as counting the number of successes in $n$ trials for the former and just 1 trial for the latter. Now comes the Geometric distribution, which counts something completely different.

We’ll start with the Story of the Geometric distribution. Imagine, similar to the Binomial, that we are conducting repeated, independent trials. The trials can either result in a success or failure, and the probability of success on every trial is $p$. If $X \sim Geom(p)$, then $X$ is the number of failures before we achieve our first success (not counting the success).

What’s a good example to really illustrate what this means? Say that we are interested in the number of times we would have to roll a fair, six-sided die until we get a 6. Here, rolling the 6 is the success, and rolling anything but a 6 is a failure. Therefore, we have a probability of $\frac{1}{6}$ for success on every trial, and $\frac{5}{6}$ for failure on every trial (remember, the trials are independent). We could say that the number of failures until success (number of times we roll the die before rolling the 6, and it’s key that we don’t count the roll of the eventual success) is distributed $Geom(\frac{1}{6})$.

The Expectation of the Geometric distribution is simply $\frac{1-p}{p}$, which simplifies to $\frac{1}{p} - 1$. Does this make sense? Well, if something occurs 5$\%$ of the time, than we expect it to occur 1 in 20 tries, since 1 is 5$\%$ of 20. What we just did is pretty much what the Geometric expectation is saying: if we reasoned that the $5\%$ event will occur 1 in 20 tries, than it’s reasonable to think on average that it will take 20 - 1 = 19 tries before we see a success (we expect to see a success on the 20th try, and we don’t want to count the success). This is a long-winded explanation, but it helps to sort of give context as to why we have this value for expectation, especially because this ‘off by one’ structure can be kind of confusing. Again, take note that we are not counting the success here. We could parameterize the random variable differently and say that our distribution counts the number of failures before the success and the success and the expectation would become just $\frac{1}{p}$ (in this case, we would call this a “First Success” distribution, which we will see in a moment). The convention with the Geometric, though, will be to not count the eventual success.

The Variance of the Geometric distribution is $\frac{1-p}{p^2}$. Unfortunately, there is not much here we can do by way of intuition to reason through this.

Lastly, and perhaps most importantly, the PMF of $X$, if $X \sim Geom(p)$, is:

\[ P(X = x) = (1-p)^x(p)\]

We can in fact intuit our way out of this one. Let’s go back to the die roll, where we hoped that we get a 6 and counted the number of failures (non-6 rolls) before that 6. Say that you wanted to find the probability that the number of failures before you rolled a 6 was 4 (that is, $x=4$). What’s the only way that this can occur? Well, you roll 4 non-sixes, and then roll one 6. The probability of each of the non-sixes is $(1 - p)$, or here, $(1 - \frac{1}{6}) = \frac{5}{6}$, and the probability of the 6 is $p$, or here $\frac{1}{6}$. Since each roll is independent, we can multiply and get $(1 - \frac{1}{6})^4(\frac{1}{6})$ to get the probability that all of the events occur, which is what the PMF would give. We don’t have to worry about any sort of counting complications because there is only one permutation: 4 non-sixes and one 6, which must come at the end of the sequence, and all of the non-sixes are identical. Even though the PMF can be tedious to work through, it helps us to understand the distribution on a deeper level.

You can further explore the Geometric distribution with our Shiny app; reference this tutorial video for more.

Click here to watch this video in your browser. As always, you can download the code for these applications here.

First Success

We just learned about the Geometric distribution, which counts the number of failures before the first success for repeated, independent trials with a constant probability $p$ of success. The First Success distribution counts the numbers of failures and the first success; it’s simply the Geometric shifted by 1. That is, if $X \sim Geom(p)$ and $Y = X + 1$, then $Y \sim FS(p)$, where $FS$ stands for First Success.

It seems foolish to define a completely new distribution based on this technical counting difference, but it simply makes it easier to consider different counting cases (sometimes we want to count the first success, sometimes we don’t, so we might as well develop the machinery for both cases). The expectation of a First Success is $1/p$, which is intuitive (as we explained above, if $p = .05$, we expect one success in 1/.05 = 20 trials, but this time we want to count the success). We can also see that this is simply 1 plus the expectation of a $Geom(p)$ random variable, which makes sense (since we can think of a First Success random variable as a Geometric random variable plus 1).

The PMF of a $X \sim FS(p)$ random variable is given by:

\[P(X = x) = (1 - p)^{x - 1}p\]

This actually has similar intuition to the PMF of a Geometric (and even looks similar although, of course, it is off by 1). Imagine the event $X = 5$. This means we want 4 failures, and then 1 success (remember, this distribution counts the success). What is the probability of 4 failures and 1 success? Simply $(1 - p)^4$ (since each failure has probability $1 - p$, and 4 in a row has probability $(1 - p)^4$ because the trials are independent and thus we can multiply marginal probabilities) times $p$ (the eventual probability of success). Again, we know we don’t have to adjust for any overcounting, since there is only one way to get 4 failures and then one success (i.e., there is no other way to order the word FFFFS, where F is failure and S is success, such that we have 4 failures first and then 1 success. If we ordered this FFSFF, for example, then we really observed $X = 3$, or 2 failures before the first success). In this case, we had $(1 - p)^4p$ for $P(X = 5)$, so in the general case we have $P(X = x) = (1 - p)^{x - 1}p$, as given above ($x - 1$ failures and then one success).

The variance of a First Success is given by $\frac{1-p}{p^2}$. Again, not much to intuit; however, it is interesting that the variance is the same as a Geometric. We haven’t learned enough about properties of variance to prove this rigorously yet or even understand it on a deeper level, but realize that we are just shifting a random variable by a constant, so the variance (‘spread’) shouldn’t really change. The location of the distribution changes, but the spread remains the same.

Negative Binomial

Much like how the Binomial is an extension of the Bernoulli, the Negative Binomial is actually an extension of the Geometric (even though the name is misleading, because it appears to connect somehow to the Binomial). The Story goes: if $X \sim NBin(r,p)$, then $X$ counts the number of failures before our $r^{th}$ success, where each trial has probability $p$ of success.

You can see how this is an extension of the Geometric; in fact, $NBin(1,p)$ is the same as $Geom(p)$, since in both cases we are counting the number of failures before the first success. You can see how it’s very similar to the Binomial-Bernoulli connection: both are the same when dealing with 1 trial (in the case of the Binomial-Bernoulli) or 1 success (in the case of the Geometric-Negative Binomial). Of course, we’ll mostly be using the Negative Binomial for cases of greater than 1 success: for example, if we were interested in the number of tails before we flipped 3 heads (generally, you will not see $NBin(1,p)$, since you could just write $Geom(p)$ for the sake of elegance).

The Expectation and Variance of the Negative Binomial are very similar to the Geometric, but multiplied by $r$: $\frac{r(1-p)}{p}$ and $\frac{r(1-p)}{p^2}$. Let’s think about why the expectation makes sense: we have basically the same set-up as the Geometric, but with $r$ times the successes needed, so it makes sense that we’ll have $r$ times the failures.

Lastly, let’s take a look at the PMF of a Negative Binomial:

\[P(X = x) = {x + r - 1 \choose r -1}p^r(1-p)^x\]

This looks intimidating at first glance, but let’s approach it the same way we did with the Geometric. First, the ‘probability part’: the $p^r$ and $(1-p)^x$. Let’s envision the probability that we get 5 tails before we get 3 heads when flipping a fair coin (here, Heads are successes and Tails are failures). One possible iteration is TTTTTHHH. To find this probability, of course, we can raise the probability of success to the number of successes: just $.5^3$, which is $p^r$ in general. Then, we multiply by the probability of the five failures, which is $(1-.5)^5$, or $(1-p)^x$ in general (yes, in this case, the successes and failures have the same probability so the terms combine to $.5^8$, but in general you won’t have $p = 1 - p = .5$ and thus the terms won’t combine). So, we agree with the probability part, but why the binomial coefficient term? Well, unlike the Geometric, where there was only one way to organize the failures and singular success, here there are multiple ways. We imagined the example of TTTTTHHH, but HHTTTTTH would also work. How do we count those ways? Well, we know that the final trial must be a success (since the experiment is over when you find the last success), so we have to find all the possible ways to order the other $r - 1$ successes with the $x$ failures. In this coin example, we know that the last coin must be an H, but then we still have to order the other two heads and the five tails. That’s just ${7 \choose 2}$, which is the same as ${x + r - 1 \choose r -1}$ (choose the locations for the heads, and then the locations for the tails are determined. You could also choose the tails first, of course: this counts the same thing, by the symmetry of the binomial coefficient). So, the key is that we are ordering all of the failures and all of the successes but one (the last one, since its place is given: it must end the sequence).

You can further explore the Negative Binomial distribution with our Shiny app; reference this tutorial video for more.

Click here to watch this video in your browser. As always, you can download the code for these applications here.

Poisson

Thanks to its characteristics, which we will discuss in a moment, the Poisson is one of the most widely used distributions in modeling real-world phenomena.

The Story goes: if we have many chances at success (i.e., many trials), each with a very small probability of success, then we can use the Poisson to model the total number of occurrences of the event. One example might be lottery tickets: many lottery tickets are sold (there are many chances at success) but the probability that any one ticket is the jackpot winner is very low. If $X$ were the number of jackpot winners, then, $X \sim Pois(\lambda)$. You can think of the parameter $\lambda$ as sort of the number of occurrences of the rare events/successes (more on this parameter later).

One of the reasons that the Poisson is so useful is that we can use it for approximations. Here is another example of where the Poisson is relevant, often called the Poisson Paradigm: if we have multiple events $A_1, A_2, ... , A_n$ where $n$ is large (so we have many events), and some $P(A_j) = p_j$ where $p_j$ is small (so $p_j$ is the slim chance that event $A_j$ occurs) then the number of events that actually occur can be modeled by $Pois(\lambda)$ where $\lambda = \sum_{j=1}^{n} p_j$. This is extremely useful because, if we are approximating, then we don’t need all of the $A_j$ events to be independent (they can be weakly dependent) or all of the $p_j$ probabilities to be the same (they can be slightly different).

Obviously ‘weakly’ and ‘slightly’ are hard to quantify; don’t really worry about this here, we’re just trying to show how this can be used as an approximation. In the real world, where things aren’t perfect, there may be some small level of dependence and the probabilities may be slightly different. Since we are approximating, it’s no big deal.

So, you should think of the Poisson Paradigm as a sort of application of the story to the real world. It can also help you understand the nature of the distribution. Most importantly, though, the Poisson Paradigm sheds light on what the parameter $\lambda$ means. Thanks to the Paradigm, you can think of the parameter $\lambda$ as sort of a ‘rate of occurrence’ or ‘number of occurrences’; after all, it is the sum of the probabilities of a bunch of events $A_j$, which we know (via the Fundamental Bridge) is just the expectation of all of these Bernoulli random variables (i.e., we can say that ‘$A_1$ occurring’ is a Bernoulli random variable with probability $p_1$ of success).

Both the Expectation and Variance of a Poisson are $\lambda$. Thinking about the expectation can help us to understand the $\lambda$ parameter even more: remember that we said that this gives the rate of occurrence of a rare event, so it makes sense that on average we will get this value. Say that we expect that 5 lottery tickets win out of all of the lottery tickets out there. Then, $\lambda = 5$, which makes sense in terms of expectation because we expect to see 5 winners throughout all of the lottery tickets. The Variance is less intuitive, but it is easy to remember, since it is the same as the expectation!

The PMF of a Poisson is:

\[P(X = x) = \frac{e^{-\lambda} \lambda^x}{x!}\]

Where $x \in \{0,1,2,..., \infty\}$.

Unfortunately, there is not much we can do with this PMF by way of intuition. An interesting thing about this PMF, though, is that, as $n \rightarrow \infty$ and $p \rightarrow 0$ (lots of trials with very small probability of success on each trial) a $Bin(n,p)$ converges to a Poisson distribution. You can prove this with the Binomial PMF: it actually becomes the Poisson PMF (although this takes a fair amount of algebra). Anyways, the point is that when you have a ton of trials with small probabilities, computing with the Binomial can be challenging (need a lot of computing power for such large parameters). Using the Poisson as an approximation can make life much easier. It also makes sense because it matches the story of a Poisson: lots of opportunities for success (large $n$) but small probability of success each time (small $p$).

The Poisson has other connections to more distributions that we’ll study; just remember that it’s a very useful distribution, especially for approximating real world counts. You can further explore the Poisson distribution with our Shiny app. Reference this tutorial video for more.

Click here to watch this video in your browser. As always, you can download the code for these applications here.

Hypergeometric

Last one for today (or tomorrow, or yesterday, whenever you are reading this). Unfortunately, this distribution isn’t related to the others as neatly as we’ve seen thus far (even though it sounds like an ‘excited’ Geometric distribution). The Story goes: if $X \sim HGeom(w,b,n)$, then $X$ counts the number of successes in $n$ draws from a population of $b$ undesired objects and $w$ desired objects (picking $w$ is marked as a success, $b$ as a failure) without replacement (you don’t put an object back after you pick it).

A concrete example to envision this is to think of a jar with $b$ blue balls and $w$ white balls. If you are drawing $n$ balls total and are hoping to pick the white balls and not pick the blue balls and you then $X$ be the number of white balls that you pick, then $X$ has a Hypergeometric distribution, specifically $X \sim HGeom(w, b, n)$.

The Expectation of a Hypergeometric is $\frac{nw}{w+b}$. This expectation is reasonable; when you start to draw, the probability that you select a white ball is the number of white balls ($w$) divided by the total amount of balls ($w + b$), and you draw $n$ times (although, of course, the probabilities of drawing a white ball do change as we conduct the experiment; this explanation is merely for intuition).

The Variance is complicated. We’re not going to include it here because it doesn’t help with any type of intuition, but you can always reference it (as well as facts about all of the important distributions) on Professor Blitzstein and William Chen’s cheatsheet.

Finally, we again reach the PMF. For a Hypergeometric, we have:

\[P(X = x) = \frac{ {w \choose x} {b \choose n - x}}{ {w + b \choose n}}\]

This is definitely the most complicated looking PMF we have seen thus far, but we are still able to work through it intuitively. A big key here, which we haven’t really dealt with yet, is that we are picking without replacement. After a ball comes out, it’s out of the bag for good; this means chiefly that trials are not independent (the make-up of the bag changes because balls are constantly being removed). Picking a lot of white balls now decreases the chances of picking white balls later (there’s just less in the bag).

So, our PMF has to deal with that ‘dynamic’ structure, since the bag changes every pick. Since we are choosing balls out of the bag, we can just count the number of ways to select the desired amount (if we wanted $P(X = 3)$, count the number of ways to select 3 white balls). After all, we remember from the ‘Sampling Table’ in Chapter 1 that the binomial coefficient models counting without replacement.

This shouldn’t be too bad, right? If we are selecting $n$ balls, then we should quickly see that there are a total of ${w + b \choose n}$ combinations for selecting these balls. That goes in the denominator, since it is the total number of outcomes. Let’s consider the numerator: the desired number of outcomes, where we pick an $x$ number of desired $w$ balls. Of course, there are ${w \choose x}$ ways to select these balls, and then, with $n-x$ selections left over for the $b$ undesired balls, there are ${b \choose n - x}$ ways to choose the rest of the balls. We multiply them (multiplication rule) and divide by the total number of outcomes, which gives us our the above PMF.

You can further explore the Hypergeometric distribution with this Shiny app; reference this tutorial video for more.

Click here to watch this video in your browser. As always, you can download the code for these applications here.

Expectation, Indicators and Memorylessness

Now that we’ve discussed all sorts of random variables, it’s a good time to talk about some related topics that arise, especially with these distributions. Chiefly, we’re going to talk about Expectation, Indicator Random Variables, and Memorylessness.

Expectation

We started to talk about Expectation in the Chapter 2, and we sort of discussed a brute force formula to calculate it. Specifically:

\[E(X) = \sum\limits_{i} x_iP(X=x_i)\]

We’re going to discuss this specific formula more in the coming chapters, and we’ll push a little deeper on expectation in general now. First, Expectation is a linear operator, which means for our purposes it has a couple of nice properties:

\[E(X + Y) = E(X) + E(Y), \; E(aX) = aE(X)\]

For random variables $X$ and $Y$ and constant $a$. A key note: the first expression holds even if $X$ and $Y$ are dependent random variables. This is where we get Linearity of Expectation, which is the name for the expression on the left: the expectation of the sum of random variables is just the sum of the expectations of the random variables. More on this when we get to Indicators.

Expectation is also linked to Variance. Keep these following expressions in mind when you need to find the Variance of a random variable:

\[Var(X) = E(X^2) - (E(X))^2\]

Generally, $(E(X))^2$ is pretty easy to find (just square the mean), but $E(X^2)$ is trickier; we’ll get to that in Chapter 4. For now, just remember that Variance originates from every point’s distance from the mean squared.

Indicators

Indicator random variables (Indicators for short) are extremely useful tools for solving problems, even if they don’t seem relevant at first. Technically, Indicators are just Bernoulli random variables: $I_A$ is an Indicator random variable that takes on the value 1 if event $A$ occurs, and the value 0 if event $A$ does not occur. We can say that $A$ occurs with probability $p$, so $P(I_A = 1) = p$ and $P(I_A=0) = 1 - p$ (just think of it as a light that switches on if some event happens, and stays off otherwise).

From here, we can use the Fundamental Bridge, alluded to earlier with the Bernoulli distribution, which basically states that the probability that an event occurs is also the expectation of the Indicator random variable (makes sense, since $I_A$ takes on value 1 with probability $p$ and value 0 with probability $1-p$). Formally, $E(I_A) = P(I_A = 1) = p$.

This seems so simple; how could Indicators be useful? It’s difficult to envision until you see an example. The basic principle is that when you have a problem that looks convoluted and you are asked for an expectation amidst a complicated set-up, you can often define simple Indicator random variables for each outcome. Then, by linearity of expectation and the fundamental bridge, you can sum up the expectations of all of the Indicator random variables to get the expectation of the event as a whole. Again, probably tough to visualize; let’s do an example. We saw this problem in Chapter 2, where we learned how to calculate probabilities associated with matches. We’ll re-introduce the problem here and instead focus on finding an expectation.

Example 3.1 (Hospital Problem, re-visited):

Say that there are $n$ couples on a given day at the hospital and they each have 1 baby, so that there are $n$ total babies in the hospital. Due to some mishap, though, the nurses lose all medical records and don’t know which baby is which. So, they just start giving each couple a random baby, and, since there are $n$ couples and $n$ babies, every couple gets a baby. What is the expected number of couples that get their own baby back?

Pattern-recognition is a very important part of solving problems in this book; that is, it’s important to realize what type of problem is being asked so that you can figure out what tool is best to use. The key here is that you have this sort of crazy scenario with all types of possibilities, and the question is asking for an expectation or average. These are hot button words that should make you think that Indicator random variables may be the best tools.

Let’s define $X$ as the number of families that get their baby back. We can also define $I_j$ as an indicator variable that the $j^{th}$ family gets their baby back; of course, $j$ runs from 1 to $n$ to cover all of the couples (if the $j^{th}$ couple gets their baby back, then $I_j = 1$). It’s a certainty, then, that $X = \sum_{j=1}^{n} I_j$. That is, the total number of couples that get their baby back is just the sum of the indicators for all couples (this is a big step, so be sure to convince yourself of it. If you think of indicator random variables as lights that ‘turn on’ when their event occurs, just think of $X$ as the number of these ‘lights’ that ‘turn on’).

Now, then, we are actually very close to finding our answer. By linearity, $E(X)$ equals the sum of the expectations of all of the Indicators: $E(I_1 + I_2 ... + I_n) = E(I_1) + E(I_2) ... + E(I_n)$. This might feel weird at first, since we’re not sure if the indicators are independent; in fact, they are definitely dependent (for example, if every other couple gets their baby back, then you know that you will get your baby back). However, remember that linearity of expectation holds even in dependent cases!

Anyways, it’s now just a matter of finding the expectation of the indicators. Since all of the families are the same in the eyes of the problem, the expectation should be the same for each indicator. And, by the fundamental bridge, we know that the expectation of the indicators is just the probability that the indicator takes on the value 1 (probability that the event occurs). So, if we can find the probability that the Indicator is 1 (the probability that one family gets their baby back), we can just multiply by $n$ and be done. That is, we have:

\[E(I_1) + E(I_2) + ... + E(I_n) = nE(I_1) = nP(I_1 = 1)\]

Of course, for any one couple, they can get $n$ possible babies, and only 1 is their own, so they have a $\frac{1}{n}$ chance of getting their baby back (this is where the problem can differ across contexts: finding the probability of the event). Multiply this by $n$ people and we expect exactly 1 family to get their baby back.

Such a simple answer for such a complicated problem! For this type of problem, it is useful to think about the simple cases: when $n = 1$, we of course expect 1 couple to get their baby back (there is only one couple and one baby!). When $n = 2$, half of the time each couple gets their baby back and half of the time neither does, so we have an average of $(.5)(2 + 0) = 1$ babies back. This sort of ‘trade-off’ - lower probabilities of matches, but more potential matches - continues as $n$ grows, and the expectation (incredibly) always balances to 1. We can confirm this result with a simulation in R.

#replicate
set.seed(110)
sims = 1000

#define different values of n to iterate over
n = 2:10

#keep track of mean number of matches
means = rep(NA, length(n))

#iterate over n
for(j in 1:length(n)){
  
  #count number of matches
  match = rep(0, sims)
  
  #run the loop
  for(i in 1:sims){
    
    #generate the 'random order' to give the babies out
    babies = sample(1:n[j])
    
    #calculate 'ratios' of couple-to-baby. If the couple gets
    #   their baby, ratio should be 1
    ratios = babies/(1:n[j])
    
    #count how many matches we got
    match[i] = length(ratios[ratios == 1])
  }
  
  #find the mean
  means[j] = mean(match)
}

#should be a vector filled with 1
means

## [1] 1.042 1.035 0.987 0.999 0.981 1.022 1.006 1.005 1.026

Hopefully this example illuminated the power of indicator random variables. This was a relatively easy problem, but only because the expectation of the indicator was easy to find (often the expectation of an indicator, or the probability that an event occurs will be more difficult to calculate). The set-up is generally pretty consistent: define an indicator, sum all of them, find the expectation of one indicator (which, again, is just the probability) and multiply it by the number of indicators there are. Remember, if you see a structurally large, complicated scenario with a lot of possible outcomes asking for an expectation, you should probably be thinking indicators. This is definitely a tricky concept and not something that you’ll likely master right away, but practice makes perfect. If you need any more convincing about the usefulness of indicator random variables, consider this ‘speed dating’ problem:

Click here to watch this video in your browser.

Memorylessness

Memorylessness is a ‘property of random variables.’ Perhaps the best way to describe it is to think about waiting for your food in a restaurant. Say that $T$ is the amount of time you spend waiting for your food, $E(T) = 10$, and $T$ has this ‘memoryless’ property. Given that $T$ is memoryless, it does not matter how long you have been waiting for you food; you still should expect to wait the same amount going forward (which is 10 minutes here because $E(T) = 10$). That is, no matter what has happened in the past, you still have the same expected wait time going forward (and, in fact, the distribution of $T$ going forward is the same as the marginal distribution of $T$). Obviously this might not hold too often in the real world; if you’ve been waiting 9 minutes for your food, you probably shouldn’t expect to wait another 10 (it will likely come sooner because the real process is not memoryless). If you’ve been waiting 5 hours for your food, you probably shouldn’t expect to have to wait 10 more minutes (something probably happened in the kitchen, and it’s unlikely that your food will come out at all!).

So, what random variable have we already learned about that seems like it could fit this property? Well, the random variable in which we are waiting for something to happen is the Geometric: we are waiting for the first failure. How could we test if the Geometric is in fact memoryless? If we can prove…

\[P(X \geq n + k | X \geq n) = P(X \geq k)\]

…then a distribution is memoryless. This is pretty intuitive: given that we have already waited for $n$ minutes, what’s the probability that we wait for $k$ more (left side of the equation)? Well, if the distribution is memoryless, than it should be the same as waiting for $k$ minutes from the very beginning (right side of the equation).

Let’s try and prove memorylessness, then, with the Geometric. First, we should consider the CDF of a Geometric random variable. Let $X \sim Geom(p)$. The CDF is defined by $P(X \leq x) = 1 - P(X > x)$. Consider the RHS: for the event $X > x$ to occur, we need at least $x + 1$ failures (since $X$ counts the number of failures and this ensures that, at the least, we will have more than $x$ failures). Since the probability of failure is $q$, we know $P(X > x) = q^{x + t}$ and thus the CDF is given by $P(X \leq x) = 1 - q^{x + t}$. From here, recalling our knowledge of conditional probability, which states that $P(A|B) = \frac{P(A \cap B)}{P(B)}$, we can re-write the above as:

\[P(X \geq n + k | X \geq n) = \frac{P(X \geq n + k \; \cap \; X \geq n)}{P(X \geq n)}\]

The numerator simplifies to $P(X \geq n + k)$, since if $X$ is greater than $n + k$ it’s also greater than $n$ (that is, the intersection is just when $X$ is greater than or equal to $n + k$, since the set $X \geq n + k$ is a subset of $X \geq n$). Now, since we just have the probabilities that $X$ is greater than or equal to some value, we essentially have the complement of the CDF, or just one minus the CDF evaluated at the point minus 1 (that is, $P(X \geq n) = 1 - P(X < n) = 1 - P(X \leq n - 1)$). Putting it all together:

\[\frac{P(X \geq n + k)}{P(X \geq n)} = \frac{q^{n + k}}{q^n} = q^k\]

This is clearly the same as $P(X \geq k) = 1 - P(X < k)$, which means that the Geometric distribution is indeed memoryless. After waiting for $n$ failures to see a success, the probability of seeing $k$ more failures until a success does not change. That is, going forward, you still have the same Geometric distribution. Thinking conditionally, in this case, doesn’t give any more information!

It might be helpful to test this property in R. We can generate ‘wait times’ from a Geometric distribution using rgeom, and then compare the overall histogram to the histogram of ‘wait times’ conditioned on waiting for more than a specific time; the histogram should not change. We can compare this to similar plots for the Binomial distribution, which is not memoryless and thus the ‘wait time’ changes when we condition on waiting longer than $k$ time units!

#replicate
set.seed(110)
sims = 1000

#define simple parameters (n, p for binomial and geometric) and value of k
n = 10
p.geom = 1/10
p.binom = 7/10
k = 5

#generate the r.v.s
X = rgeom(sims, p.geom)
Y = rbinom(sims, n, p.binom)

#graphics
#set graphic grid
par(mfrow = c(2,2))

#overall histogram
hist(X, main = "X ~ Geom(p)", xlab = "", freq = FALSE,
     col = rgb(1, 0, 0, 1/4))

#condition
hist(X[X > k] - k, main = "(X - k)|X > k", freq = FALSE,
     xlab = "", col = rgb(1, 0, 0, 1/4))


#overall histogram
hist(Y, main = "Y ~ Bin(n, p)", xlab = "", freq = FALSE,
     col = rgb(0, 0, 1, 1/4))

#condition
hist(Y[Y > k] - k, main = "(Y- k)|Y > k", freq = FALSE,
     xlab = "", col = rgb(0, 0, 1, 1/4))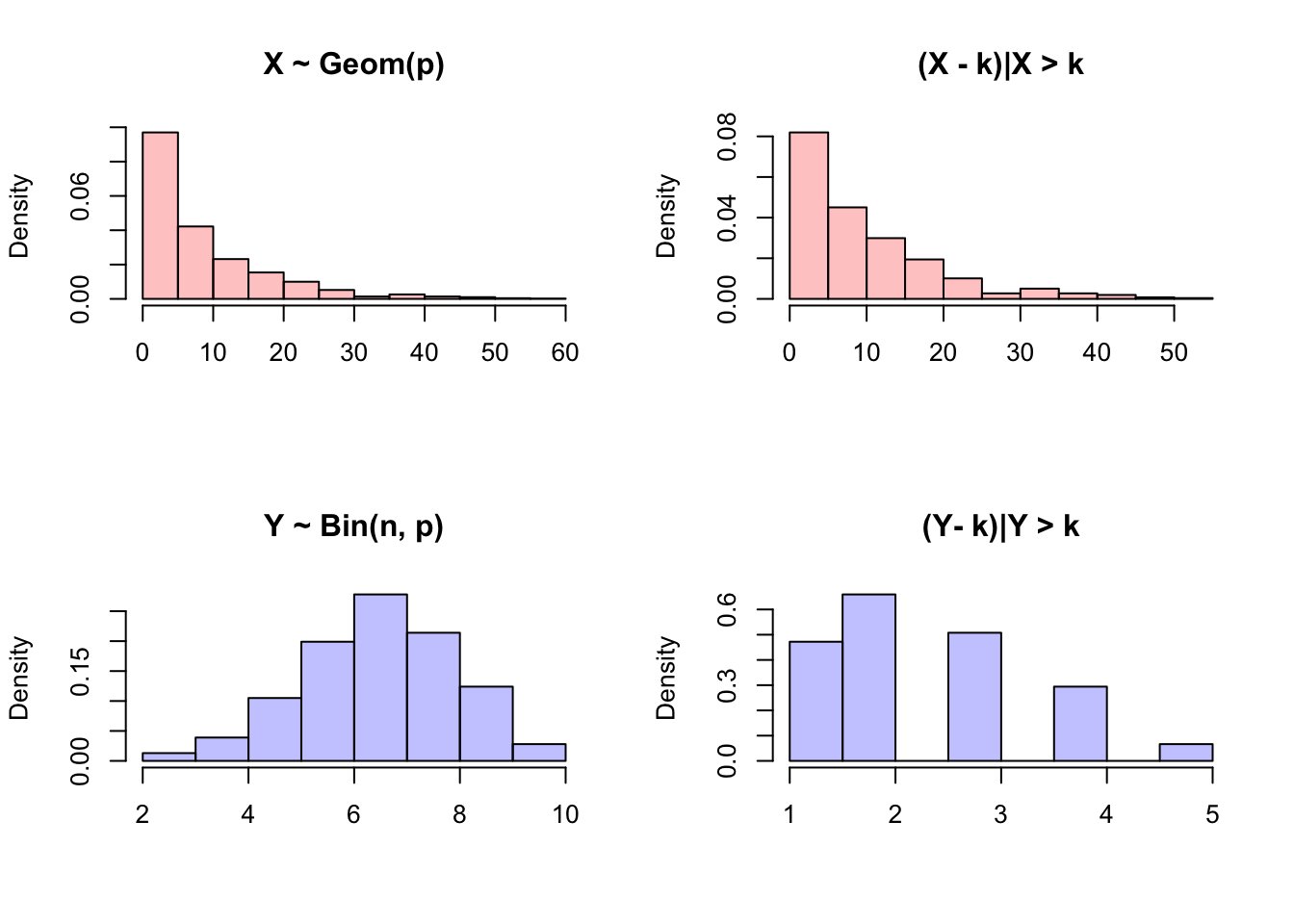

#re-set graphic state
par(mfrow = c(1,1))

We’ll see more of memorylessness in the future, especially when we delve into continuous random variables; for now, remember the concept of the property, and that it applies to the Geometric distribution. In fact, in the discrete case, it only applies to the Geometric distribution; there is no other memoryless discrete distribution!

Practice

Problems

3.1

With help from Matt Goldberg

You are playing a game of Russian Roulette with one other person. The rules of game are as follows: a bullet is placed randomly in one of six chambers of a gun, and the players take turns pulling the trigger (if the bullet chamber comes up, the bullet fires and the player loses, otherwise the gun does not fire and the game continues). Every time the trigger is pulled, the chambers rotate so that a new chamber comes into the ‘firing position’ (so at maximum, the gun is fired six times).

If you would like to maximize your chances of winning this game, should you go first or second?
Re-solve part (a) in the case of a game of Russian Roulette using a gun with $n$ chambers, where $n \geq 2$ is an even number.
Re-solve part (b) in the case where $n > 2$ is an odd number. Discuss what happens as $n \rightarrow \infty$.
Return to the conventional set-up of the game as described at the start of the problem. Let $X$ be the number of blanks fired (trigger pulls before the bullet is fired, not including the bullet firing). Remember that the game ends when the bullet is fired. Explain why $X$ is NOT Geometric.
Continuing as in (d), find $E(X)$.

3.2

(Help from Matt Goldberg) The Negative Hypergeometric distribution is a discrete distribution that takes three parameters, $n$ = total number of balls, $k$ = number of white balls, and $r$ = number of black balls when the experiment is stopped (i.e., after observing $r$ black balls, we stop drawing balls). If $X \sim NHgeom(n, k, r)$, then $X$ counts the number of white balls sampled from $n$ balls (without replacement) until we have sampled $r$ black balls.

Explain how this distribution is similar to and different from a Hypergeometric distribution.
If $X \sim NHgeom(n, k, r)$, $E(X) = \frac{rk}{n - k + 1}$. Use this fact to provide a more elegant Solution to 3.1 (the Russian Roulette problem.)

3.3

Let $X \sim Pois(c\lambda)$, where $c$ is a positive integer. Let $Y \sim Pois(\lambda)$ and $Z \sim cY$. Are $X$ and $Z$ identically distributed? That is, do they have the same distribution (i.e., two quarters, when flipped, are different random variables, but both have a $Bern(1/2)$ distribution if we are counting the number of heads)?

3.4

Nick’s favorite word is ‘no.’ In fact, he loves the word ‘no’ so much that he employs the following pattern of speech: for every word he speaks, he says ‘no’ with probability $1/4$ and some word other than ‘no’ with probability $3/4$, independently across words. You have a conversation with Nick where he says $n \geq 3$ words. Find the expected number of times that he says “no no no.” If he says “no no no no,” this counts as two “no no no” phrases (the first ‘no’ to the third ‘no,’ and then the second ‘no’ to the fourth ‘no’).

3.5

The first chord in the song Bohemian Rhapsody by Queen is a ‘B flat 6,’ which is correctly played with 4 distinct keys on a 88 key piano.

You randomly select 4 distinct keys on a piano and play them together (as a chord) until you play the B flat 6 (in the correct key; again, there are only 4 correct keys). Let $X$ be the number of chords you play (including the B flat 6), and find $E(X)$.

Hint: Remember, a Geometric random variable ‘doesn’t count the success,’ but a First Success distribution does.

The first lyrics in the song are “Is this the real life”. Imagine that you speak words at random until you have dictated these opening lyrics verbatim. Let $Y$ be the number of words you speak until you have recited these lyrics. Explain why $Y$ does not have the same distribution as $X$ (not just the same distribution with a different parameter, but a different distribution altogether).

3.6

Datamatch is a Harvard Valentine’s day program where you fill out a questionnaire and are matched based on some ‘compatability scores’ with other students who filled out the questionnaire.

Say, for the purpose of this problem, that Harvard Datamatch is undergoing some reconstruction. Instead of giving you your top 10 matches as in the past, intimacy is being brought up a notch, and you are only given one match: the top person that you were compatible with. However, sadly, that doesn’t necessarily mean that they were matched with you: they could be given anyone. Say also that, even more unfortunately, the secret love algorithm is just a random generator that assigns you your top ‘match’ completely randomly, and there is no special sauce behind the scenes (you have an equal chance of getting everyone else in Datamatch as your top match).

Finally, you can’t be matched with yourself, and assignments do not have to be unique (one person can be the top match for multiple other people). This year, 100 people decided to fill out Datamatch.

Say that you are one of the 100 people doing Datamatch and are given your true love for your top intimacy match. What is the probability that they also got you as their top match?
A ‘lovebird pair’ occurs when two people get each other as their top intimacy match. Let $M$ be the number of lovebird pairs. Find $E(M)$.

3.7

Recall the ‘hospital problem.’ There are $n$ couples (two parents), each of which has exactly 1 child. There is a mix-up at the hospital, and the $n$ children are distributed randomly among the $n$ couples. Let $X$ be the number of couples that get their baby back.

As a refresher, find $E(X)$.
Approximate $P(X = 0)$, the probability that no one gets their baby back, as $n \rightarrow \infty$.

3.8

There are 50 states in the USA; assume for this problem that you have been to none of them. You visit the states at random (for each ‘round’ you randomly select one of the 50 to visit, even if you have already visited it) until you have visited every state. On average, how many visits will you make before you visit every state?

3.9

Let $I_A$ and $I_B$ be the indicators for events $A$ and $B$, respectively. Let $p_A = P(A)$ and $p_B = P(B)$. Find the distribution of $I_A^{I_B}$.

3.10

(With help from Juan Perdomo)

Recall the ‘pentagon problem,’ which we will restate here.

Consider these 5 points:

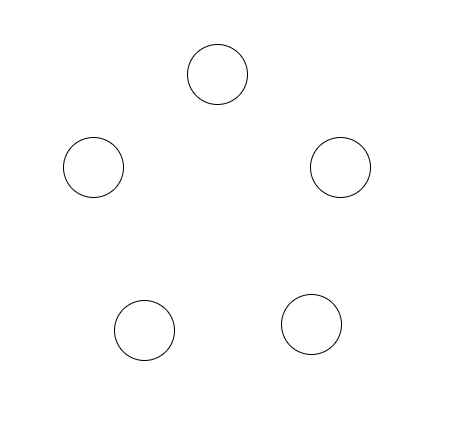
You can make plots like this in Latex here.

Imagine selecting two points at random and drawing a straight line in between the two points. Do this 5 times, with the constraint that you cannot select the same pair twice. What is the probability that the lines and points form a pentagon (i.e., a five-sided, five-angled, closed shape)?

We saw this problem earlier in a counting context. Now, solve this problem using the Hypergeometric distribution.

3.11

There are $n$ people with red hats and $n$ people with blue hats in a room. The people randomly pair off (i.e., they are each randomly paired with another person). Let $X$ be the number of pairs with matching hat colors (i.e., a pair where both people have red hats).

Find $E(X)$.
Let $Y$ be the number of pairs that don’t have matching hat colors (one in the pair has a red hat and one has a blue hat). Find $E(Y)$.
Which is larger, $E(X)$ or $E(Y)$? Why? How do they compare for large $n$?
What is $E(X) + E(Y)$?

3.12

Imagine a table with $n$ chairs. Each round, we ‘toggle’ each chair (chairs can either be occupied or empty, and ‘toggling’ means to switch to the other state, like from empty to occupied) independently with probability 1/2 (if we don’t toggle a chair, it stays in the same state). Let $X_t$ be the number of filled seats at round $t$, and start at $t = 1$.

Find $E(X_t)$.
Let $M$ be the first time that $X_t = n$; that is, the first time that the table is full. Find $E(M)$.

3.13

Imagine a restaurant with $n > 1$ tables. Each table has $k \leq n$ chairs. There are $n$ people in the restaurant, and they are randomly assigned to the chairs in the restaurant. Let $X$ be the number of empty tables. Find $E(X)$.

3.14

We know that the Geometric distribution is memoryless, and if $Y \sim Geom(p)$, that $(Y + 1) \sim FS(p)$.

Find the CDF of $X$ if $X \sim FS(p)$.
Recall the technical condition for memorylessness:

\[P(X \geq n + k | X \geq n) = P(X \geq k)\]

Test to see if $Y$ is memoryless.

Provide some intuition for your result in part b.

3.15

This problem is dedicated to Renan Carneiro, Nicholas Larus-Stone, CJ Christian, Juan Perdomo, Matt Goldberg and Dan Fulop.

“President” is a popular card game, and is played with a standard 52-card deck. Let’s consider a 4-person game. Each player is given a ‘title’ based on their past performance in the game. The best two players are “president” and “vice president” (best and second best, respectively) and the bottom two players are “scum” and “vice scum” (worst and second worst, respectively). Each player is dealt a random 13-card hand from the well-shuffled deck. The president gets to choose the two best cards in the scum’s hand; he then gives the scum his two worst cards. A similar transaction occurs between the vice president and vice scum, but with just 1 card.

The best card in the game is a 2, and since this is a standard deck, there are four 2’s in the deck (one for each suit).

Find the expected number of 2’s that each player gets before the ‘transactions’ (i.e., the hand they are dealt before they swap cards).
Assume that the president will always try to take as many 2’s as possible from the vice scum (and that he will never give up a 2). Let $X$ be the number of 2’s that the president will end up with post-transaction (after he has taken two cards from the scum). Find $E(X)$.

Hint: Consider $Y$, the number of 2’s the scum gets post transaction.

Explain why your answer to part (b) is not 2.

3.16

You are dealt a random 5-card hand from a standard, well-shuffled 52-card deck. Let $X$ be the number of Aces that you get. Find $Var(X)$.

3.17

Let $I_j$ be the indicator that you roll a $j$ on one roll of a fair die, and let $X = I_1 + I_2 + ... + I_6$. Nick claims that $X \sim Bin(1, 1/6)$, since $X$ is the sum of $Bern(1/6)$ r.v.’s. Argue for or against his claim.

3.18

Juan is reading a book with 10 pages. He starts on page 3 and flips forward a page (i.e., page 3 to 4) with probability $p$ and backwards with probability $1 - p$. What is the probability that he flips to the end of the book (flips to page 10) before flipping backwards more than once?

3.19

A binary number is a number expressed in the base-2 numeral system; it only includes the digits 0 and 1. It is perhaps best understood with an example. The binary number…

\[1 \; 0 \; 1 \; 1 \; 0\]

…can easily be written in our standard, decimal (base-10) system, by raising each digit in the binary number to the appropriate value of 2 (based on its location in the string). That is, we convert to decimal with the calculation $2^5 + 0 + 2^3 + 2^1 + 0 = 42$ (since there is a ‘1’ in the ‘fifth’ spot - that is, five spots from the left - so this marks that we should add $2^5$, and there is a 0 in the fourth spot, so we don’t have to add anything here).

Consider a binary number with $n$ digits. How many possible decimal numbers can we express with this binary number?

For the next two parts, consider a binary number with $n$ digits, where each digit is randomly assigned 0 or 1 with equal possibilities. Let $X$ be decimal value of this binary number (i.e., the value when we translate it to base-10).

Find the probability that $X$ is even.
Find the distribution of $X$.

3.20

This riddle is a common interview problem:

A king has imprisoned 10 subjects. He offers the prisoners a strange way that they can play for their release: each day, he will randomly and independently call one of the 10 prisoners in. That prisoner will be allowed to either guess if all of the prisoners have already been called in, or ‘pass’ and return to the dungeon for another day. If a prisoner correctly guesses that all of the prisoners have been called in already, the prisoners are set free; otherwise, they lose.

The prisoners are kept in different cells and are not allowed to communicate except through one strange channel: in the kings’ chamber sits a standard, two-sided coin, and every day, the prisoner that is randomly selected to be summoned may choose to flip the coin over (heads to tails or tails to heads) or simply leave the coin unflipped. The coin starts with heads showing.

The ‘random sampling’ of the king (picking one of the 10 prisoners each day) is truly random and independent across days. The prisoners are allowed to discuss a strategy session before entering their cells. How can they guarantee their escape?

The answer to the riddle is a follows: the prisoners assign one prisoner to be the ‘White Knight’ who simply keeps track of the number of prisoners that have been called. To do this, the prisoners institute a rule: if a prisoner that is not the White Knight is summoned and he sees that the coin shows heads, he flips the coin over to show tails. From there, no other non-White Knight prisoner will flip the coin (it shows tails, not heads) and when the White Knight enters and sees the coin showing tails, he will add one to his count and flip the coin back over to show heads (the process begins again). Once a non-White Knight prisoner has flipped the coin from heads to tails, he doesn’t flip it again, even if he sees heads (to avoid double-counting). When the White Knight has flipped the coin 9 times (he has counted the other 9 prisoners) he can safely tell the king that all of the prisoners have been called.

If the prisoners use this strategy, how long will it take, on average, for them to be freed? How does this compare to the actual average amount of time that it will take for each prisoner to be called in?

BH Problems

The problems in this section are taken from Blitzstein and Hwang (2014). The questions are reproduced here, and the analytical solutions are freely available online. Here, we will only consider empirical solutions: answers/approximations to these problems using simulations in R.

BH 3.18

In the World Series of baseball, two teams (call them A and B) play a sequence of games against each other, and the first team to win four games wins the series. Let $p$ be the probability that A wins an individual game, and assume that the games are independent. What is the probability that team A wins the series?
Give a clear intuitive explanation of whether the answer to (a) depends on whether the teams always play 7 games (and whoever wins the majority wins the series), or the teams stop playing more games as soon as one team has won 4 games (as is actually the case in practice: once the match is decided, the two teams do not keep playing more games).

BH 3.28

There are $n$ eggs, each of which hatches a chick with probability $p$ (independently). Each of these chicks survives with probability $r$, independently. What is the distribution of the number of chicks that hatch? What is the distribution of the number of chicks that survive? (Give the PMFs; also give the names of the distributions and their parameters, if applicable.)

BH 3.29

A sequence of $n$ independent experiments is performed. Each experiment is a success with probability $p$ and a failure with probability $q=1-p$. Show that conditional on the number of successes, all valid possibilities for the list of outcomes of the experiment are equally likely.

BH 3.37

A message is sent over a noisy channel. The message is a sequence $x_1,x_2, \dots, x_n$ of $n$ bits ($x_i \in \{0,1\}$). Since the channel is noisy, there is a chance that any bit might be corrupted, resulting in an error (a 0 becomes a 1 or vice versa). Assume that the error events are independent. Let $p$ be the probability that an individual bit has an error ($0<p<1/2$). Let $y_1, y_2, \dots, y_n$ be the received message (so $y_i = x_i$ if there is no error in that bit, but $y_i = 1-x_i$ if there is an error there).

To help detect errors, the $n$th bit is reserved for a parity check: $x_n$ is defined to be 0 if $x_1 + x_2 +\dots + x_{n-1}$ is even, and 1 if $x_1 + x_2+ \dots + x_{n-1}$ is odd. When the message is received, the recipient checks whether $y_n$ has the same parity as $y_1 + y_2+ \dots + y_{n-1}$. If the parity is wrong, the recipient knows that at least one error occurred; otherwise, the recipient assumes that there were no errors.

For $n=5,p=0.1$, what is the probability that the received message has errors which go undetected?
For general $n$ and $p$, write down an expression (as a sum) for the probability that the received message has errors which go undetected.
Give a simplified expression, not involving a sum of a large number of terms, for the probability that the received message has errors which go undetected.

BH 3.42

Let $X$ be a random day of the week, coded so that Monday is 1, Tuesday is 2, etc. (so $X$ takes values 1,2,…,7, with equal probabilities). Let $Y$ be the next day after $X$ (again represented as an integer between 1 and 7). Do $X$ and $Y$ have the same distribution? What is $P(X < Y)$?

BH 4.13

Are there discrete random variables $X$ and $Y$ such that $E(X) > 100E(Y)$ but $Y$ is greater than $X$ with probability at least 0.99?

BH 4.17

A couple decides to keep having children until they have at least one boy and at least one girl, and then stop. Assume they never have twins, that the “trials” are independent with probability 1/2 of a boy, and that they are fertile enough to keep producing children indefinitely. What is the expected number of children?

BH 4.18

A coin is tossed repeatedly until it lands Heads for the first time. Let $X$ be the number of tosses that are required (including the toss that landed Heads), and let $p$ be the probability of Heads, so that $X \sim FS(p)$. Find the CDF of $X$, and for $p=1/2$ sketch its graph.

Hint: Recall that a First Success ($FS$) distribution is a Geometric where we count the success.

BH 4.20

Let $X \sim \textrm{Bin}(n,\frac{1}{2})$ and $Y \sim \textrm{Bin}(n+1,\frac{1}{2})$, independently. (This problem has been revised from that in the first printing of the book, to avoid overlap with Exercise 3.25.)

Let $V = \min(X,Y)$ be the smaller of $X$ and $Y$, and let $W = \max(X,Y)$ be the larger of $X$ and $Y$. So if $X$ crystallizes to $x$ and $Y$ crystallizes to $y$, then $V$ crystallizes to $\min(x,y)$ and $W$ crystallizes to $\max(x,y)$. Find $E(V) + E(W)$.
Show that $E|X-Y| = E(W)-E(V),$ with notation as in (a).
Compute $Var(n-X)$ in two different ways.

BH 4.22

Alice and Bob have just met, and wonder whether they have a mutual friend. Each has 50 friends, out of 1000 other people who live in their town. They think that it’s unlikely that they have a friend in common, saying “each of us is only friends with 5% of the people here, so it would be very unlikely that our two 5%’s overlap.”

Assume that Alice’s 50 friends are a random sample of the 1000 people (equally likely to be any 50 of the 1000), and similarly for Bob. Also assume that knowing who Alice’s friends are gives no information about who Bob’s friends are.

Compute the expected number of mutual friends Alice and Bob have.
Let $X$ be the number of mutual friends they have. Find the PMF of $X$.
Is the distribution of $X$ one of the important distributions we have looked at? If so, which?

BH 4.24

Calvin and Hobbes play a match consisting of a series of games, where Calvin has probability $p$ of winning each game (independently). They play with a “win by two” rule: the first player to win two games more than his opponent wins the match. Find the expected number of games played.

BH 4.26

Let $X$ and $Y$ be $Pois(\lambda)$ r.v.s, and $T = X + Y$. Suppose that $X$ and $Y$ are not independent, and in fact $X=Y$. Prove or disprove the claim that $T \sim {Pois}(2\lambda)$ in this scenario.

BH 4.29

A discrete distribution has the memoryless property if for $X$ a random variable with that distribution, $P(X \geq j + k | X \geq j) = P(X \geq k)$ for all non negative integers $j,k$.

If $X$ has a memoryless distribution with CDF $F$ and PMF $p_i = P(X=i)$, find an expression for $P(X \geq j+k)$ in terms of $F(j), F(k), p_j,p_k.$
Name a discrete distribution which has the memoryless property. Justify your answer with a clear interpretation in words or with a computation.

BH 4.30

Randomly, $k$ distinguishable balls are placed into $n$ distinguishable boxes, with all possibilities equally likely. Find the expected number of empty boxes.

BH 4.31

A group of $50$ people are comparing their birthdays (as usual, assume their birthdays are independent, are not February 29, etc.). Find the expected number of pairs of people with the same birthday, and the expected number of days in the year on which at least two of these people were born.

BH 4.32

A group of $n \geq 4$ people are comparing their birthdays (as usual, assume their birthdays are independent, are not February 29, etc.). Let $I_{ij}$ be the indicator r.v. of $i$ and $j$ having the same birthday (for $i<j$). Is $I_{12}$ independent of $I_{34}$? Is $I_{12}$ independent of $I_{13}$? Are the $I_{ij}$ independent?

BH 4.33

A total of $20$ bags of Haribo gummi bears are randomly distributed to 20 students. Each bag is obtained by a random student, and the outcomes of who gets which bag are independent. Find the average number of bags of gummi bears that the first three students get in total, and find the average number of students who get at least one bag.

BH 4.40

There are 100 shoelaces in a box. At each stage, you pick two random ends and tie them together. Either this results in a longer shoelace (if the two ends came from different pieces), or it results in a loop (if the two ends came from the same piece). What are the expected number of steps until everything is in loops, and the expected number of loops after everything is in loops? (This is a famous interview problem; leave the latter answer as a sum.)

BH 4.44

Let $X$ be Hypergeometric with parameters $w,b,n$.

Find $E {X \choose 2}$ by thinking, without any complicated calculations.
Use (a) to find the variance of $X$. You should get \[Var(X) = \frac{N-n}{N-1} npq,\] where $N=w+b, p =w/N, q = 1-p$.

BH 4.47

A hash table is being used to store the phone numbers of $k$ people, storing each person’s phone number in a uniformly random location, represented by an integer between $1$ and $n$ (see Exercise 25 from Chapter 1 for a description of hash tables). Find the expected number of locations with no phone numbers stored, the expected number with exactly one phone number, and the expected number with more than one phone number (should these quantities add up to $n$?)

BH 4.50

Consider the following algorithm, known as bubble sort, for sorting a list of $n$ distinct numbers into increasing order. Initially they are in a random order, with all orders equally likely. The algorithm compares the numbers in positions 1 and 2, and swaps them if needed, then it compares the new numbers in positions 2 and 3, and swaps them if needed, etc., until it has gone through the whole list. Call this one ``sweep" through the list. After the first sweep, the largest number is at the end, so the second sweep (if needed) only needs to work with the first $n-1$ positions. Similarly, the third sweep (if needed) only needs to work with the first $n-2$ positions, etc. Sweeps are performed until $n-1$ sweeps have been completed or there is a swapless sweep.

For example, if the initial list is 53241 (omitting commas), then the following 4 sweeps are performed to sort the list, with a total of 10 comparisons: \[ 53241 \to 35241 \to 32541 \to 32451 \to 32415.\] \[ 32415 \to 23415 \to 23415 \to 23145.\] \[ 23145 \to 23145 \to 21345.\] \[ 21345 \to 12345.\]

An inversion is a pair of numbers that are out of order (e.g., 12345 has no inversions, while 53241 has 8 inversions). Find the expected number of inversions in the original list.
Show that the expected number of comparisons is between $\frac{1}{2} {n \choose 2}$ and ${n \choose 2}.$

BH 4.52

An urn contains red, green, and blue balls. Balls are chosen randomly with replacement (each time, the color is noted and then the ball is put back). Let $r,g,b$ be the probabilities of drawing a red, green, blue ball, respectively ($r+g+b=1$).

Find the expected number of balls chosen before obtaining the first red ball, not including the red ball itself.
Find the expected number of different colors of balls obtained before getting the first red ball.
Find the probability that at least 2 of $n$ balls drawn are red, given that at least 1 is red.

BH 4.53

Job candidates $C_1,C_2,...$ are interviewed one by one, and the interviewer compares them and keeps an updated list of rankings (if $n$ candidates have been interviewed so far, this is a list of the $n$ candidates, from best to worst). Assume that there is no limit on the number of candidates available, that for any $n$ the candidates $C_1,C_2,...,C_n$ are equally likely to arrive in any order, and that there are no ties in the rankings given by the interview.

Let $X$ be the index of the first candidate to come along who ranks as better than the very first candidate $C_1$ (so $C_X$ is better than $C_1$, but the candidates after $1$ but prior to $X$ (if any) are worse than $C_1$. For example, if $C_2$ and $C_3$ are worse than $C_1$ but $C_4$ is better than $C_1$, then $X = 4$. All $4!$ orderings of the first 4 candidates are equally likely, so it could have happened that the first candidate was the best out of the first 4 candidates, in which case $X > 4$.

What is $E(X)$ (which is a measure of how long, on average, the interviewer needs to wait to find someone better than the very first candidate)?

Hint: Find $P(X>n)$ by interpreting what $X>n$ says about how $C_1$ compares with other candidates, and then apply the result of Theorem 4.4.8.

BH 4.62

Law school courses often have assigned seating to facilitate the Socratic method. Suppose that there are 100 first-year law students, and each takes the same two courses: Torts and Contracts. Both are held in the same lecture hall (which has 100 seats), and the seating is uniformly random and independent for the two courses.

Find the probability that no one has the same seat for both courses (exactly; you should leave your answer as a sum).
Find a simple but accurate approximation to the probability that no one has the same seat for both courses.
Find a simple but accurate approximation to the probability that at least two students have the same seat for both courses.

BH 4.63

A group of $n$ people play ``Secret Santa" as follows: each puts his or her name on a slip of paper in a hat, picks a name randomly from the hat (without replacement), and then buys a gift for that person. Unfortunately, they overlook the possibility of drawing one’s own name, so some may have to buy gifts for themselves (on the bright side, some may like self-selected gifts better). Assume $n \geq 2$.

Find the expected value of the number $X$ of people who pick their own names.
Find the expected number of pairs of people, $A$ and $B$, such that $A$ picks $B$’s name and $B$ picks $A$’s name (where $A \neq B$ and order doesn’t matter).
Let $X$ be the number of people who pick their own names. What is the approximate distribution of $X$ if $n$ is large (specify the parameter value or values)? What does $P(X = 0)$ converge to as $n \to \infty$?

BH 4.65

Ten million people enter a certain lottery. For each person, the chance of winning is one in ten million, independently.

Find a simple, good approximation for the PMF of the number of people who win the lottery.
Congratulations! You won the lottery. However, there may be other winners. Assume now that the number of winners other than you is $W \sim Pois(1)$, and that if there is more than one winner, then the prize is awarded to one randomly chosen winner. Given this information, find the probability that you win the prize (simplify).

BH 4.75

A group of 360 people is going to be split into 120 teams of 3 (where the order of teams and the order within a team don’t matter).

How many ways are there to do this?
The group consists of 180 married couples. A random split into teams of 3 is chosen, with all possible splits equally likely. Find the expected number of teams containing married couples.

BH 4.76

The gambler de M’er’e asked Pascal whether it is more likely to get at least one six in 4 rolls of a die, or to get at least one double-six in 24 rolls of a pair of dice. Continuing this pattern, suppose that a group of $n$ fair dice is rolled $4 \cdot 6^{n-1}$ times.

Find the expected number of times that “all sixes” is achieved (i.e., how often among the $4 \cdot 6^{n-1}$ rolls it happens that all $n$ dice land $6$ simultaneously).
Give a simple but accurate approximation of the probability of having at least one occurrence of ``all sixes", for $n$ large (in terms of $e$ but not $n$).
de M’er’e finds it tedious to re-roll so many dice. So after one normal roll of the $n$ dice, in going from one roll to the next, with probability 6/7 he leaves the dice in the same configuration and with probability $1/7$ he re-rolls. For example, if $n=3$ and the $7$th roll is $(3,1,4)$, then $6/7$ of the time the $8$th roll remains $(3,1,4)$ and $1/7$ of the time the $8$th roll is a new random outcome. Does the expected number of times that “all sixes” is achieved stay the same, increase, or decrease (compared with (a))? Give a short but clear explanation.

BH 4.77

Five people have just won a $100 prize, and are deciding how to divide the $100 up between them. Assume that whole dollars are used, not cents. Also, for example, giving $50 to the first person and $10 to the second is different from vice versa.

How many ways are there to divide up the $100, such that each gets at least $10?
Assume that the $100 is randomly divided up, with all of the possible allocations counted in (a) equally likely. Find the expected amount of money that the first person receives.
Let $A_{j}$ be the event that the $j$th person receives more than the first person (for $2 \leq j \leq 5$), when the $100 is randomly allocated as in (b). Are $A_2$ and $A_3$ independent?

BH 4.78

Joe’s iPod has 500 different songs, consisting of 50 albums of 10 songs each. He listens to 11 random songs on his iPod, with all songs equally likely and chosen independently (so repetitions may occur).

What is the PMF of how many of the 11 songs are from his favorite album?
What is the probability that there are 2 (or more) songs from the same album among the 11 songs he listens to?
A pair of songs is a match if they are from the same album. If, say, the 1st, 3rd, and 7th songs are all from the same album, this counts as 3 matches. Among the 11 songs he listens to, how many matches are there on average?

BH 4.79

In each day that the Mass Cash lottery is run in Massachusetts, 5 of the integers from 1 to 35 are chosen (randomly and without replacement).

When playing this lottery, find the probability of guessing exactly 3 numbers right, given that you guess at least 1 of the numbers right.
Find an exact expression for the expected number of days needed so that all of the ${35 \choose 5}$ possible lottery outcomes will have occurred.
Approximate the probability that after 50 days of the lottery, every number from 1 to 35 has been picked at least once.

References

Blitzstein, J. K., and J. Hwang. 2014. Introduction to Probability. Chapman & Hall/CRC Texts in Statistical Science. CRC Press. https://books.google.com/books?id=z2POBQAAQBAJ.