3.9 Practice Problems
3.9.1
(#fig:directed_practice3_1)A directed graph
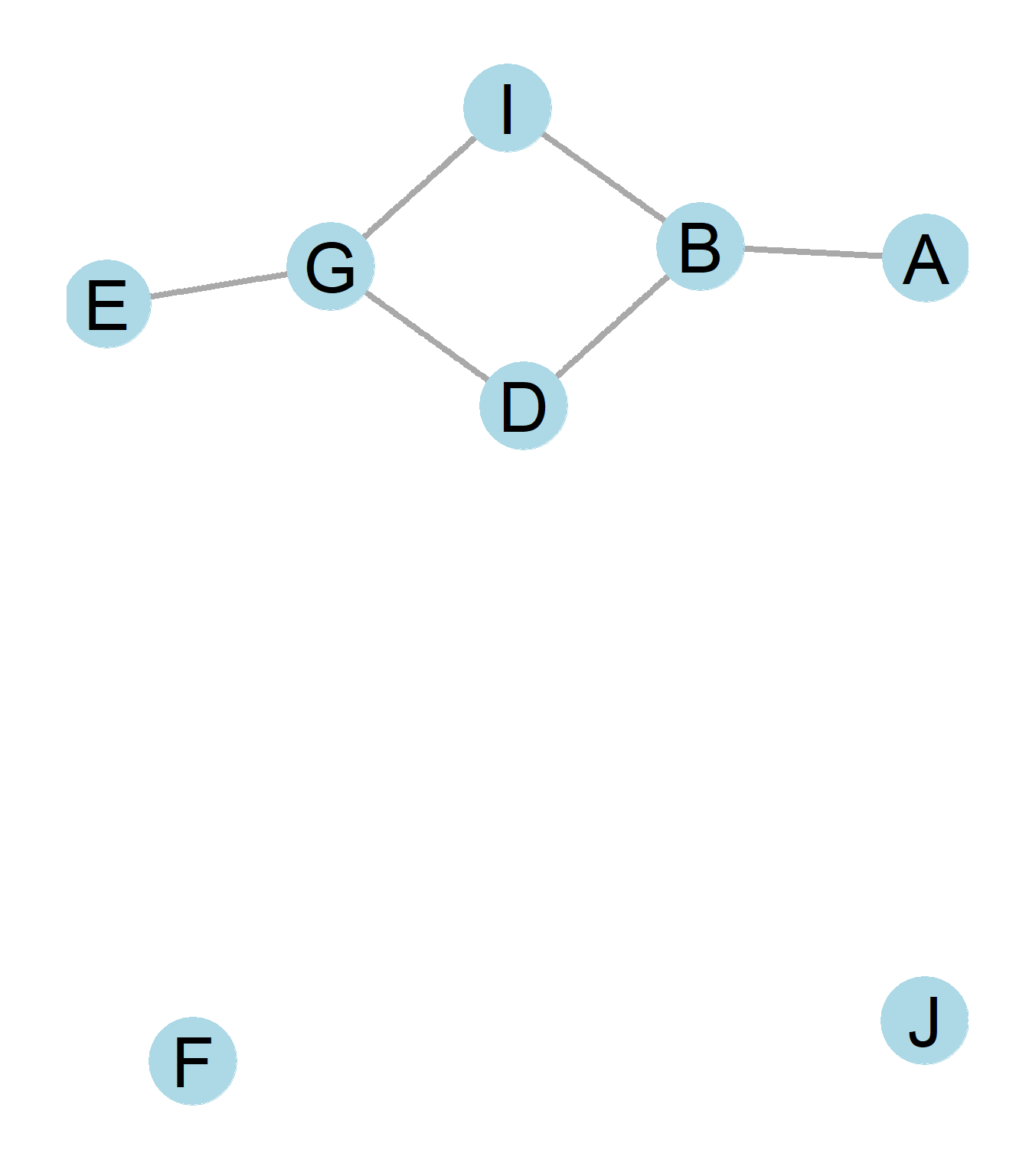
- Create a reachability matrix describing the above graph.
3.9.2
(#fig:directed_practice3_2)An undirected graph
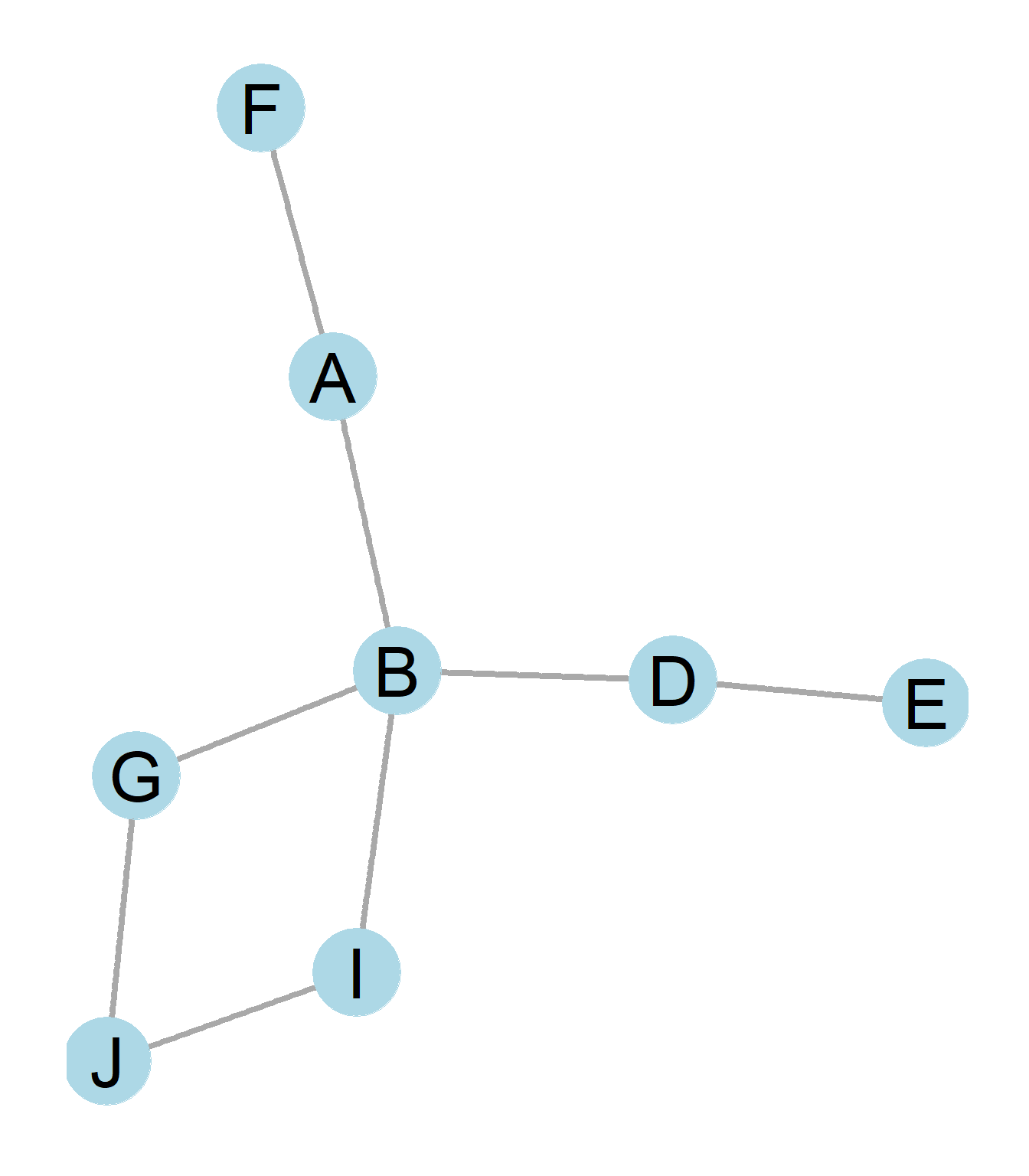
3.9.3
(#fig:directed_practice3_3)A directed graph
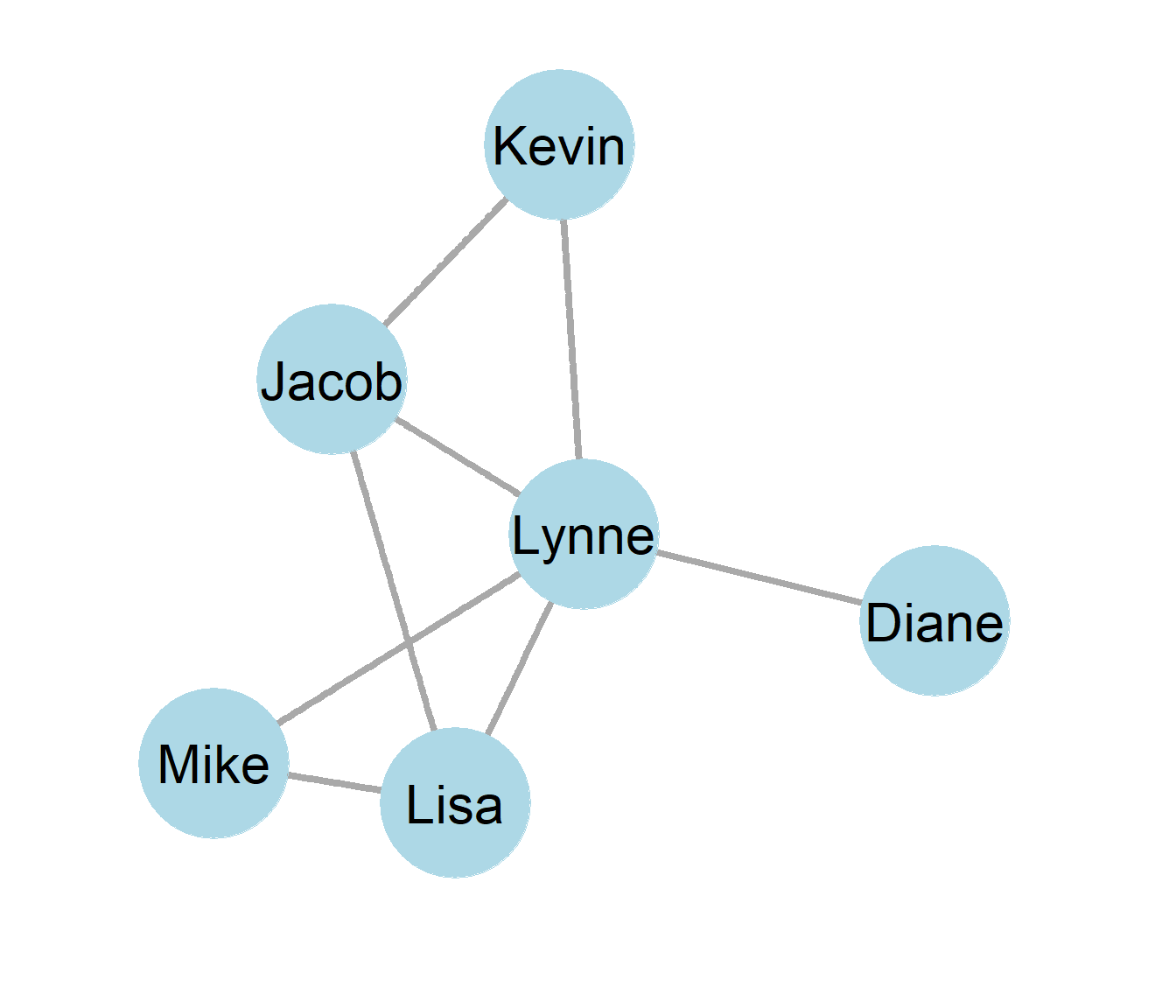
Above we have a made-up network consisting of academics who have worked together on projects that was presented in the exercises of Chapter 1. Please conduct the following exercises using data from the above graph.
- Please turn the above graph into an undirected matrix
- Is the above matrix an asymmetric, symmetric, or antisymmetric matrix?
- What are examples of non-adjacent ties in the graph?
3.9.4
Please solve the following matrix multiplication problems, if possible. \[ \begin{equation} \begin{bmatrix} 8 & 9 & 3\\ 3 & 2 & 2\\ \end{bmatrix} \begin{bmatrix} 5 & 4\\ 1 & 2\\ 3 & 2\\ \end{bmatrix} = \end{equation} \]
\[ \begin{equation} \begin{bmatrix} 2 & 1 & 4\\ \end{bmatrix} \begin{bmatrix} 3\\ 3\\ 0\\ \end{bmatrix} = \end{equation} \]
\[ \begin{equation} \begin{bmatrix} 8\\ 2\\ \end{bmatrix} \begin{bmatrix} 8 & 5\\ 7 & 6\\ 9 & 3\\ \end{bmatrix} = \end{equation} \]
\[ \begin{equation} \begin{bmatrix} 2 & 5\\ 3 & 5\\ 2 & 5\\ \end{bmatrix} \begin{bmatrix} 2\\ 3\\ \end{bmatrix} = \end{equation} \]
\[ \begin{equation} \begin{bmatrix} 5 & 9 & 1\\ 4 & 5 & 2\\ \end{bmatrix} \begin{bmatrix} 7 & 4\\ 1 & 2\\ 3 & 6 \end{bmatrix} = \end{equation} \]
\[ \begin{equation} \begin{bmatrix} 4 & 8 & 2\\ \end{bmatrix} \begin{bmatrix} 3\\ 7\\ 5\\ \end{bmatrix} = \end{equation} \]
\[ \begin{equation} \begin{bmatrix} 4\\ 5\\ \end{bmatrix} \begin{bmatrix} 4 & 8\\ 5 & 8\\ 9 & 7 \end{bmatrix} = \end{equation} \]
\[ \begin{equation} \begin{bmatrix} 4 & 8\\ 5 & 8\\ 9 & 7 \end{bmatrix} \begin{bmatrix} 4\\ 5\\ \end{bmatrix} = \end{equation} \]
3.9.5
(#fig:directed_practice3_5)An undirected graph
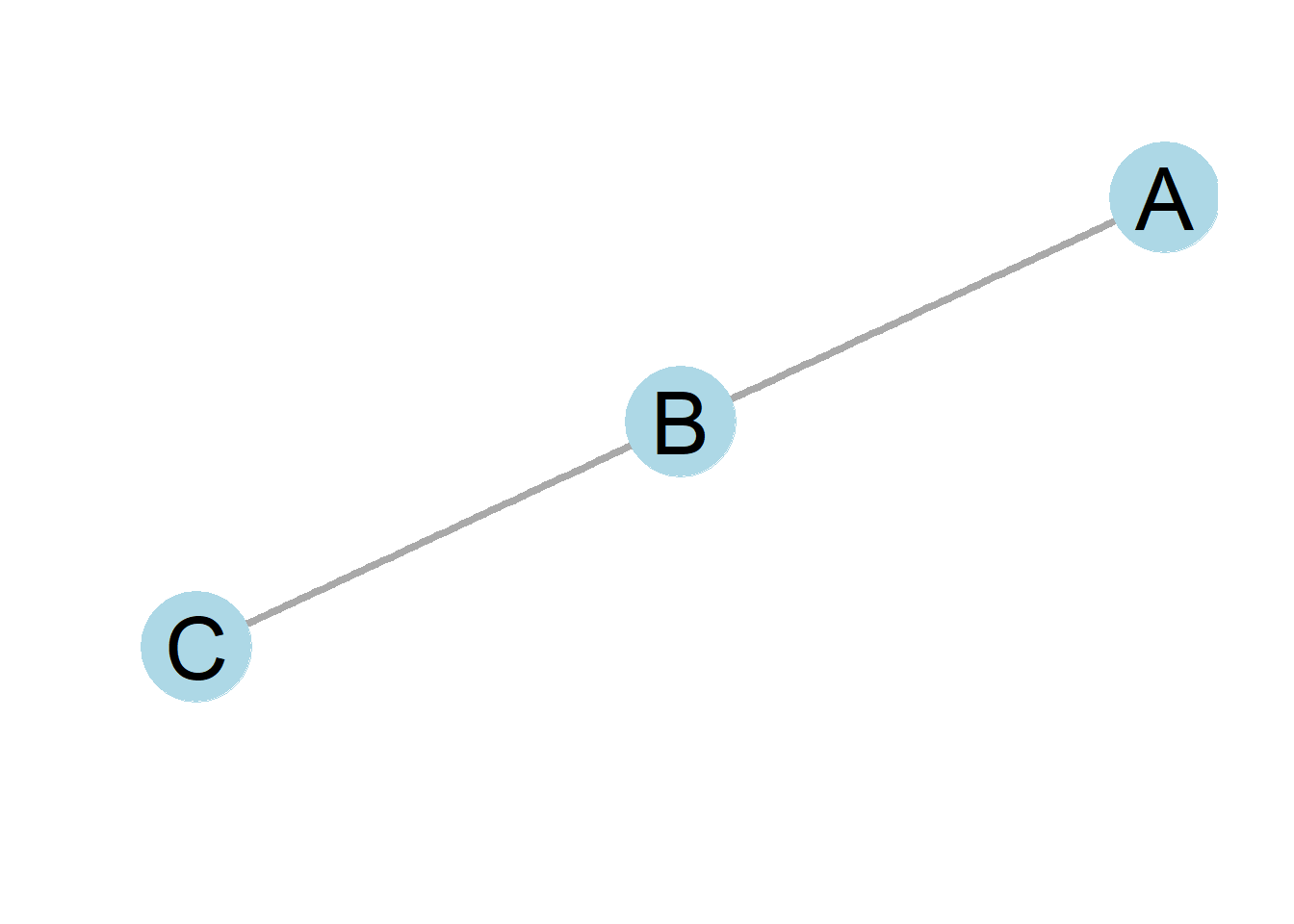
- Multiply the adjacency matrix for the above graph by itself. What is the resulting matrix and interpret the results