2.5 Anti-Symmetric Ties and Tree Graphs

There is a special type of directed relationship that has the property of only going in one direction. These are called anti-symmetric ties. Like asymmetric ties, anti-symmetric ties have a directionality (and thus source and destination nodes), but reciprocity is forbidden by definition. That means that if A is anti-symmetrically connected to B, then B cannot send the same type of tie back to A (although B may be connected, and typically is, to A via some other type of tie).

A common example of anti-symmetric ties in political sociology is patron-client ties (Martin ⊕2009Martin, John Levi. 2009. Social Structures. Princeton University Press.). Patrons can have many clients, but it is impossible for client of a patron to also be a patron to the same person. Other types of anti-symmetric ties are hierchical relations at work, and cross-generation linsk in families. Your boss is your boss, while you are not your boss’ boss. In armies ``giving orders to’’ is an anti-symmetric relation. An officer who gives orders to another officer (and thus commands them) cannot by definition also receive orders from them.

In the same way, your parents are your parents (but you can only be a son or daughter to your parents), and your grandparents are their parents, and so forth. “Being the parent of” thus counts as an anti-symmetric relation as we define here; it only goes way (from parents to children) but it cannot come back from children towards parents.

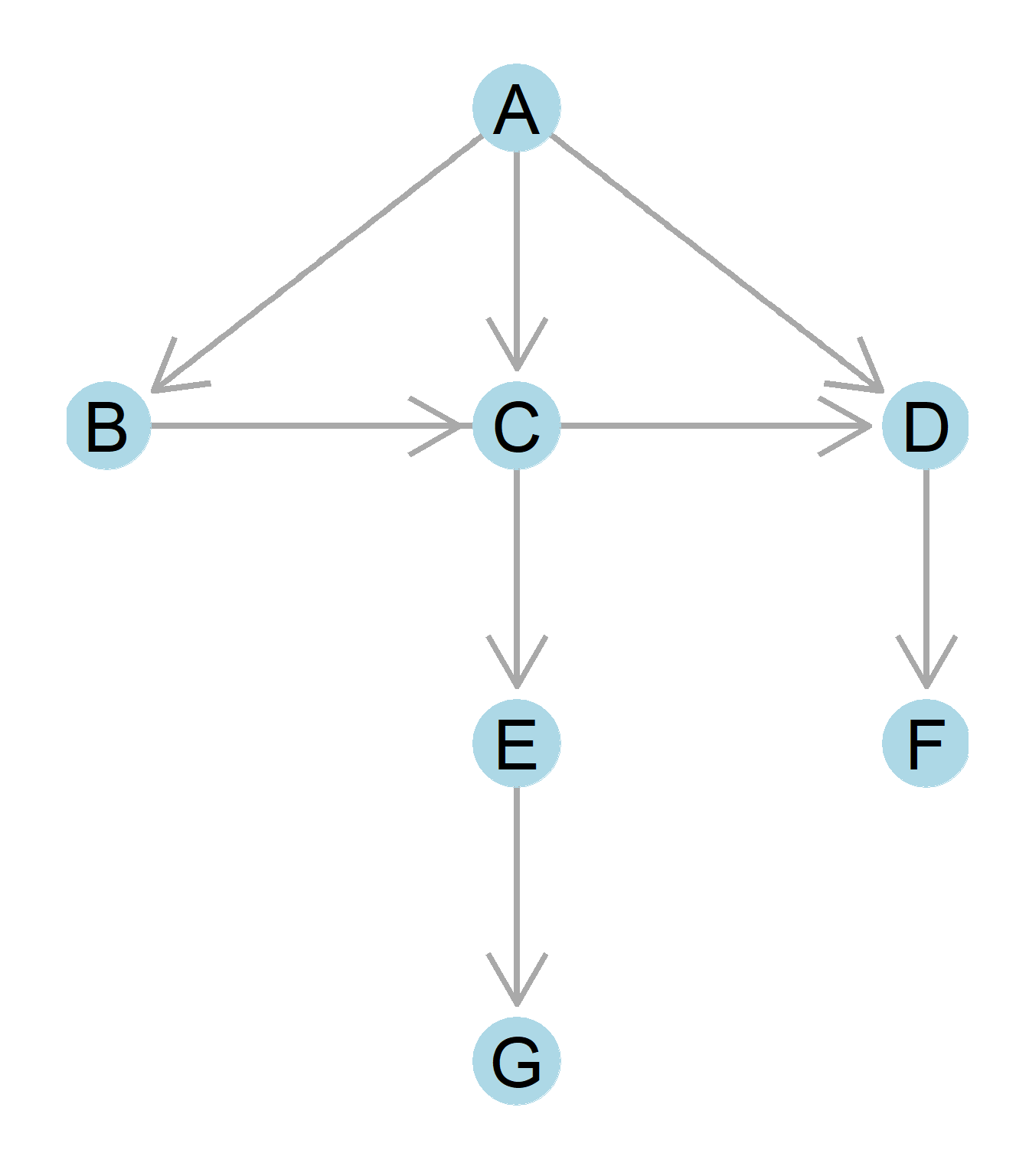Figure 0.11: A tree graph.

One feature of a network composed of only anti-symmetric relations is that its corrresponding graph can always be drawn from top to bottom, starting (at the top) with the node that only sends but does receive any ties and ending (at the bottom) with nodes that only receive, but do not send, ties. This is called a tree graph and an example, obtained from removing the reciprocal ties from Figure 0.10, is shown in Figure 0.11. Your family tree is an example of a tree graph of anti-symmetric kin ties. Teacher-student, coach-athlete, buyer-seller are all examples of anti-symmetric relationships that can be modeled as anti-symmetric networks and depcited as tree graphs.

For instance, Figure 0.11 could be a network in which the anti-symmetric links are directed “gives orders to” (in an army or an office) relations, where the source node directs commands toward the destination node. So A is the top boss and commands B, C, and D. Node B, in their turn, gives orders to C, who gives orders to C. Both B and C, are able to command nodes E and F. It is also clear from the graph that node G is at the lowest level of the hieararchy, receiving orders from E, but not commanding anybody in turn.