2.11 Weighted Ties as a Measure of Strength

In the preceding sections, our understanding of relationships have centered around their existence or absence. In certain situations, it may be socially meaningful to consider relationships in terms of their intensity or frequency- or what is often referred to as the “strength” of the tie.

For example, people might have many friends, and friendship ties can be turned into graphs as done in the above examples. However, people often have different types of friends, and some friends are more important than others. This is the concept behi0nd having a best friend. Your best friend might be more important to you than all your other friends, and it might be sociologically meaningful to the topic you are studying to capture this difference in your network. While it might be a little meaningless to just mark your best friend different from the rest, we can think of social situations where a series of gradations might make sense.

For example, let’s say that we want to understand who is the de facto leader in a group of friends. By definition, we’ve already bound the case as an existing group of friends. If everyone had a tie to the others, because they’re all friends, then we would not be able to detect any variation between these different friends. However, if we looked at the frequency of text messages sent from one of these friends to another one, then we would likely begin to detect variation.

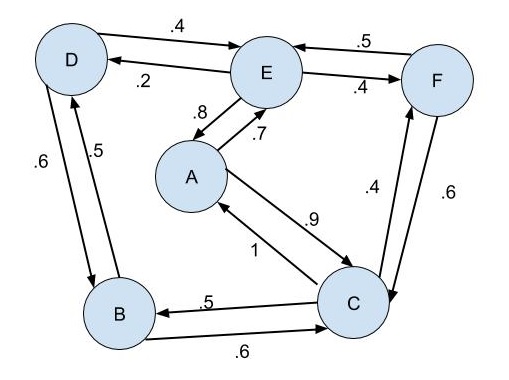
Figure 1.6

The variation in the strength of these ties is captured by weighting. Weighting is when the relative intensity of the relationships between actors in the network is mathematically standardized, thus facilitating the comparison of particular actors and relationships within the network. Thinking of Figure 1.6 as a text message or emailing network between a set of friends or coworkers at a company, the numbers can be thought of as the frequency of communication. Actors A and C communicate frequently, with C sending messages to A a little more often than A send messages to C. However, C sends messages to B half as frequently as C sends messages to A.

When one carefully looks at Figure 1.6, one can see that A is the most texted friend in the group, or the most emailed coworker. How this conclusion can be supported will be explored in greater detail in Chapter 3 in our discussion of Eigenvector Centrality, but essentially, actor E and C get more attention from actors B, D, and F than they give back. As A gives less attention to E and C than E and C give to A, A derives a central position from E and C being important to all the people A does not text.email with. While we will deal with this issue in more detail later, it is from varying weights, representing some varying frequency or intensity of the relationship in the real world, that we can understand certain social problems.