3.3 The Symmetric Adjacency Matrix

If we want to build an adjacency matrix of a network, we simply list all the actors in the rows and columns, and ask if the two share a relationship in order to fill in the values. A great way of understanding this is to start with a graph and to convert it into a matrix. This is done below where the undirected graph from Figure 0.15 is converted into its symmetric adjacency matrix equivalent.

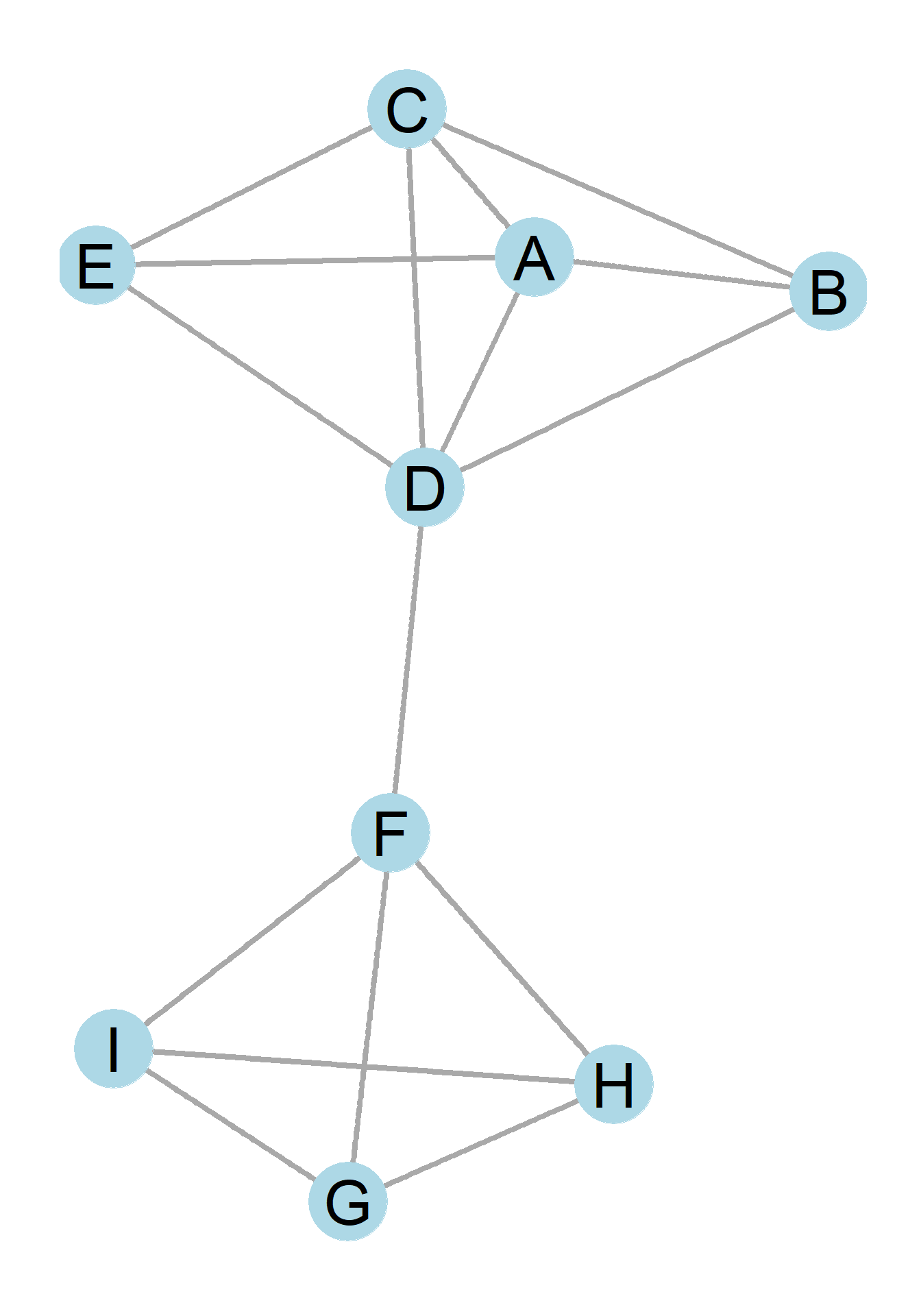Figure 0.15: A undirected graph

\[ \begin{array}{ccccccccc} & A & B & C & D & E & F & G & H & I \\ A & - & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ B & 1 & - & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ C & 1 & 1 & - & 1 & 1 & 0 & 0 & 0 & 0 \\ D & 1 & 1 & 1 & - & 1 & 1 & 0 & 0 & 0 \\ E & 1 & 0 & 1 & 1 & - & 0 & 0 & 0 & 0 \\ F & 0 & 0 & 0 & 1 & 0 & - & 1 & 1 & 1 \\ G & 0 & 0 & 0 & 0 & 0 & 1 & - & 1 & 1 \\ H & 0 & 0 & 0 & 0 & 0 & 1 & 1 & - & 1 \\ I & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & - \end{array} \]

The first step in building the adjacency matrix that represents the graph is to list all the nodes {A, B, C, D, E, F, G, H, I} as both a row and a column entry for each node. Next, one goes sequentially across the rows and columns, asking the question “does actor i have the relationship I am examining with actor j?” If the question asked is about the absence or presence of a relationship, 0’s and 1’s are used. If A has a relationship with B, the value 1 is marked. Otherwise, 0.

As we can see in matrix above, A indeed has a relationship with B, so the corresponding cell is marked 1. In fact, A has a relationship with B, C, D, and E and has 1’s in each of the cells corresponding to these actors, but not with F, G, H, or I and so 0’s are in these cells.

But what do we do about the cells where we are theoretically supposed to ask if A has a relationship with A? For most projects, it makes sense to just put a dash there. It’s not sociologically meaningful for A to have a relationship with itself in most cases. For example, asking “Is A friends with A?” does not make much sense, but there are rare cases when it does, such as when A is a group of people and not an individual, and the relationship under examination might occur both within and between groups. These are called reflexive-ties or loops, but they are quite uncommon.

After completing the first row, we ask does actor B have a relationship with actor A? Well yes, it does. In fact, we can know without even looking because if you recall, this network is defined ahead of time as reciprocal, meaning if A is friends with B, B is friends with A. We can remember this because the graph we are using is undirected. This means that the resulting matrix is going to be symmetric. Symmetric matrices are those that, when flipped along the diagonal (as shown in Figure ??), the two sides of the matrix will be mirror images of each other.