3.5 The Weighted Matrix

Remember the weighted graph from chapter 2? We can easily create a weighted matrix where, instead of using 0 and 1 to indicate the absence or presence of an edge between nodes, we use the weight as an indication of the strength of the tie between the two actors. Thus, a tie is not simply absent or present, but falls along some scale or absence to “maximum intensity,” which is a function of how the researcher thinks about the tie.

For example, your best friend might be a tie strength of 1, while people you do not know are 0’s. However, in the middle there are all types of people who fall along the spectrum between your best friend and someone you have never seen before. It might make sense if you are trying to study social influence that people’s best friend might have more influence on their choices than their 5th closest friend. What the weights for your 5th closest friend in this weighting system is a matter of research design which can be debated, but once the weights are determined, it is simple to incorporate them into a matrix.

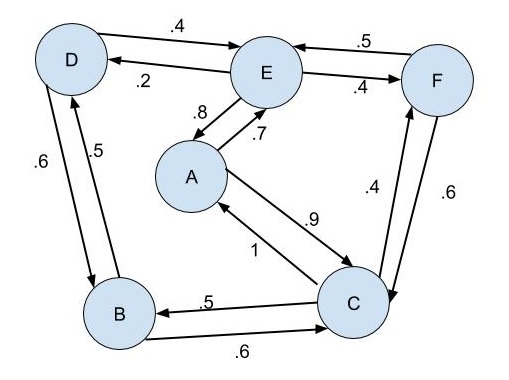(#fig:weighted_mat)A Weighted Network

\[ \begin{array}{ccccccccc} & A & B & C & D & E & F \\ A & - & 0 & .9 & 0 & .7 & 0 \\ B & 0 & - & .6 & .5 & 0 & 0 \\ C & 1 & .5 & - & 0 & 0 & .4 \\ D & 0 & .6 & 0 & - & .4 & 0 \\ E & .8 & 0 & 0 & .2 & - & .4 \\ F & 0 & 0 & 0 & .6 & .5 & - \\ \end{array} \]

This will be important when we do centrality measures in subsequent chapters. Looking at the graph, can you figure out which is highest status actor? In future chapters, we will present measures that can calculate just this question!