1.3 The Two Faces of Social Network Analysis
Social network analysis has two broad aspects. One, generally referred to as network theory is about figuring out how networks work and what networks do to and for people. In essence, social network theories are general statements about how people behave in networks and how networks themselves “behave”"; that is where network relations come from, what they do, and what consequences they have for the people involved.
For instance, the idea of social capital that is, that the connections that you have to others can bring you certain types of benefits, is part of network theory. In fact, as we will see in chapter 7, a good chunk of network theory (but not all!), such as the theory of structural holes, or the strength of weak ties theory, can be thought of as theories of social capital (Borgatti and Halgin 2011Borgatti, Stephen P, and Daniel S Halgin. 2011. “On Network Theory.” Organization Science 22 (5): 1168–81.). Other types of network theory deal with how networks of sentiment relations (e.g. likes and dislikes) form (see chapter 6), while other tell us about how things flow through networks (see chapter 9).
Figure 0.4: The two faces of Social Network Analysis.
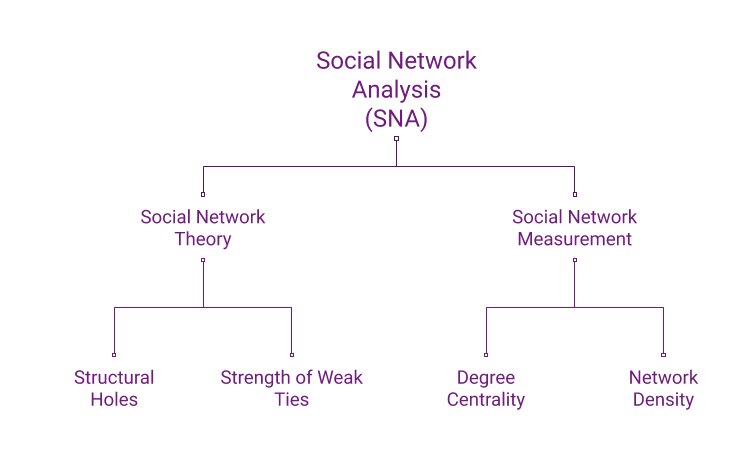
Another branch of social network analysis deals with how to measure various network properties. This branch of social network analysis, called network measurement links social network concepts to some type of matheatical or quantiative representation. Since this branch of network analysis deals with measurement, it is where mathematics and other forms of quantitative representation of networks (such as matrices) come in handy.
If math scares you, don’t worry. Our job is to walk you slowly through it. But you still may be asking: Why math though? The beauty of math, is that it allows us to take some fuzzy social science concepts, stated in natural language, such as the idea of “popularity” or “social position” or “strength of connection” and give it a precise representation. That way we can use networks to learn about what makes the social world go round or predict why some people, organizations, or even whole countries are successful and others are not (among other things).
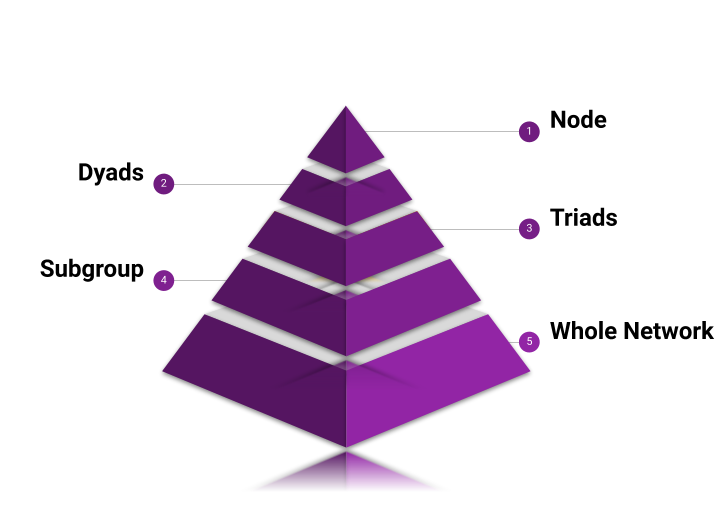
Figure 0.5: Levels of analysis in social networks.
The two “faces” of SNA (network theory and network measurement) as well as some choice examples are depicted in 0.4. Don’t get nervous if you do not know what the things at the bottom of the diagram (e.g., “density”), means. We will explain them to you in the forthcoming chapters!
We can develop theories or measure network properties at multiple levels of analysis. Like other complex systems, social networks feature dynamics at multiple nested levels. We will deal with four such leves in what follows. At the node level we may be interested in what properties nodes have by virtue of the connections they have within the network. Both the idea of an ego network and various measures of social position based on centrality are defined at this level.
At the dyad and triad levels, we may be interested in the properties that the edges or the links have by virtue of settling into certain configurations. Both the idea of tie strength and various theories dealing with triples of nodes such as Balance Theory (Davis 1963Davis, James A. 1963. “Structural Balance, Mechanical Solidarity, and Interpersonal Relations.” American Journal of Sociology 68 (4): 444–62.), Strength of Weak Ties Theory (Granovetter 1973Granovetter, Mark S. 1973. “The Strength of Weak Ties.” American Journal of Sociology 78 (6): 1360–80.), the theory of Structural Holes (Burt 1995Burt, Ronald S. 1995. Structural Holes. Harvard University Press.), and Simmmelian Tie Theory (Krackhardt 1999Krackhardt, David. 1999. “The Ties That Torture: Simmelian Tie Analysis in Organizations.” Research in the Sociology of Organizations 16 (1): 183–210.) are defined this level. At the subgroup We may be interested in properties that subset or cluster or nodes have by virtue of the set of connections they share. Here, theories and measures of group cohesion, and community structure in networks have been developed.
Finally, we may be interested in measuring properties and theorizing the structure and dynamics of the whole network. This may includes quantities that are sums or averages of features computed at lower levels, or they may include properties applicable to the system as a whole (e.g., whether it would take a short or a long time to get something from one randomly selected person in the network to another). Ideas of whether human networks constitute Small Worlds (Milgram 1967Milgram, Stanley. 1967. “The Small World Problem.” Psychology Today 2 (1): 60–67.) are defined at this level.
Figure 0.5 shows the nested structure of social networks. At all levels we can develop specific theories to understand what is happenning at that slice or develop special measures designed to link the concepts of those theories to a precise quantative representation.