2.10 Ego-Centric Networks

Ego-centric networks (or shortened to “ego” networks) are a particular type of network which specifically maps the connections of and from the perspective of a single person (an “ego”). For example, if you were to ask someone to name their friends (or any other type of “alter,” which is defined as someone who is not the ego), they will tell you who their friends are. However, they will not tell you who the friends of other people are. While in Figure 1.3 and 1.4 we had graphs of complete networks, in this case, we are only getting a small part of the overall social network.

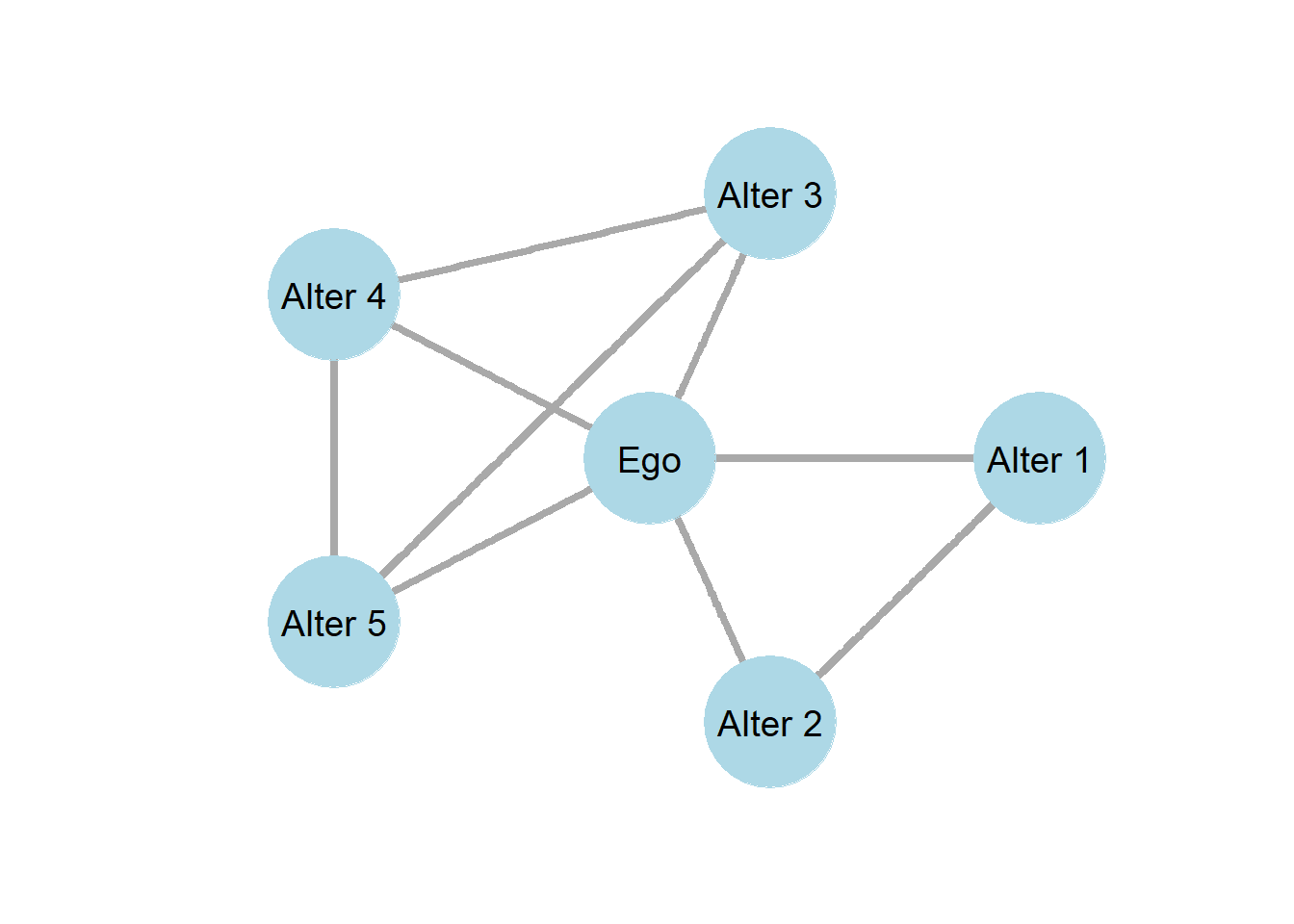Figure 1.5

While it might seem like we are unable to do much with ego-networks, that is definitely not the case! While having data on only one person’s ego does not tell scholars much, when we have tens, hundreds, or thousands of ego-networks we are able to analyze how different types of people have different ego-networks. For example, if all the students in the class fill out ego-networks of their friends and family, could we find that certain types of people have more friends? Do people with more family members also have more friends, or do they have fewer friends? These are empirical questions which, when scholars creatively compare ego-centric networks, we are able to potentially answer. Research does not have to only use one type of relationship when collecting network data, and this would be one such case when combining ego-centric networks of both friendship and family ties into a single personal network of emotional support or some other socially meaningful exchange. When discussing an ego network, size describes the number of alters that the ego has identified. Thus, the ego network graph in Figure 1.5 has a size of five.

Just as with a complete graph, we might be interested in the certain properties of the ego-network, such as how dense it is. By definition, everyone knows the ego, but to what extent does someone’s friends know each other? For ego-networks, the clustering coefficient is calculated as the density of ties amongst alters when ego is removed. As seen in Figure 1.5, some of ego’s friends do know each other. Calculating the clustering coefficient is the same as density, but with ego and ego’s ties removed.

Clustering Coefficient Calculated for Figure 1.5 \[ \begin{equation} \frac{m}{\frac{n(n-1)}{2}}=\frac{4}{\frac{5(4)}{2}}=.4 \end{equation} \]

Thus, as demonstrated by the resulting clustering coefficient, we can understand the 40% of all possible ties amongst ego’s friends exist. With multiple egos, we might thus be able to compare their personal networks to build theories about how the social world operates.