Capítulo 5 Probabilidades discretas

Empezaremos con algunos principios básicos de la data categórica. A las probabilidades de este tipo se les llama probabilidades discretas. Entender los principios básicos de las probabilidades discretas nos ayudar a entender las probabilidades continuas que son las más comunes en aplicaciones de data science.

Recordemos que una variable discreta es una variable que no puede tomar algunos valores dentro de un mínimo conjunto numerable, quiere decir, no acepta cualquier valor, únicamente aquellos que pertenecen al conjunto.

Por ejemplo, si tenemos en un salón sentados a 4 mujeres y 6 hombres e hiciésemos un sorteo de 1 premio intuitivamente sabríamos que la probabilidad de que el sorteado sea hombre es de 60%.

5.1 Cálculo usando la definición matemática

La probabilidad que obtuvimos por intuición en el ejemplo anterior se puede expresar de la siguiente forma:

\(P(A) = probabilidad\ del\ evento\ A = \frac{Veces\ en\ que\ el\ evento\ A\ se\ puede\ dar}{Total\ de\ resultados\ posibles}\)

\(P(Sorteado\ sea\ hombre) = \frac{6}{10} = 60\%\)

5.2 Simulación de Montecarlo para variables discretas

La simulación o método de Montecarlo es un método estadístico utilizado para resolver problemas matemáticos complejos a través de la generación de variables aleatorias. En este caso el problema no es complejo, pero se puede utilizar Montecarlo para ir familiarizándonos con un método que usaremos constantemente.

Usaremos simulación Montecarlo para estimar la proporción qué obtendríamos si repitiésemos este experimento de forma aleatoria un número determinado de veces. Es decir, la probabilidad del evento usando esta estimación sería la proporción de veces en que ocurrió ese evento en nuestra simulación.

En R podemos crear fácilmente muestras aleatorias utilizando la función sample(). Por ejemplo, creemos un vector de estudiantes y luego usemos la función sample(), para escoger uno al azar.

También podríamos usar la función rep() para crear más rápido el vector estudiantes. Para ello ingresaríamos como primer argumento un vector y como segundo otro vector indicando cuántas veces queremos que se creen. Así, crearíamos más rápido el vector estudiantes.

Ahora tenemos que simular un determinado número de veces el experimento de sacar un elemento aleatorio. Para ello usaremos la función replicate(). Repliquemos este experimento 100 veces:

Podemos ver cuál fue el resultado de cada uno de los 100 sorteos que simulamos.

Ahora usaremos la función table() para transformar nuestro vector resultados en una tabla resumida que nos muestre cuantas veces apareció cada valor.

Si este resultado lo almacenamos en un vector tabla_resultados, podemos luego usar la función prop.table() para saber la proporción de cada valor:

No nos debemos de preocupar por si la probabilidad de que sea hombre no nos ha salido 60% exacto. Recordemos que estamos estimando la probabilidad usando un método que depende del número de veces que simulemos el experimento. Mientras más veces repitamos el experimento más cercano estaremos al valor. Por ejemplo, repliquemos este experimento ahora 10,000 veces.

Vemos cómo el valor va convergiendo a 60%. No nos debemos de preocupar si el valor varía por algunos dígitos al presentado en este libro dado que estamos simulando un evento al azar.

Finalmente, para este ejemplo sencillo también podríamos haber utilizado la función mean(). Si bien esto nos calcula el promedio de un conjunto de números, podríamos convertir nuestro vector estudiantes a valores númericos, donde cada valor lo convirtamos en 1 o 0 dependiendo de alguna condicion.

Para ello, R nos hace muy sencilla la conversión de vectores a 1 y 0 utilizando el operador comparador ==:

Cuando aplicamos la función mean() a este resultado, ésta coerciona a los valores TRUE hacia 1 y los valores FALSE por 0. Así, si aplicamos el promedio de esta lista, tendríamos el porcentaje de hombres y con ello la probabilidad de que al escoger una persona ésta sea hombre:

5.2.1 Otras funciones para crear vectores

Ya hemos aprendido la función rep() para crear más rápido vectores. Otra función que encontramos en R es la función expand.grid(x, y) la cual nos crea un data frame de todas las combinaciones entre los vectores x e y.

Finalmente, tenemos la función paste(x,y), la cual nos concatena dos cadenas o vectores de cadenas agregando un espacio en el medio.

Así, podemos generar fácilmente, por ejemplo, una baraja de cartas distribuidas en 4 palos: corazones, diamantes, picas y tréboles. Las cartas de cada palo están numeradas del 1 al 10, donde el 1 es el As, y seguidas por Jack, la Reina y el Rey.

Para esto, tendríamos que crear un vector de palos y un vector de números para luego crear la combinatoria y tener la baraja completa.

numeros <- c("As", "Dos", "Tres", "Cuatro", "Cinco", "Seis", "Siete", 
             "Ocho", "Nueve", "Diez", "Jack", "Reina", "Rey")
palos <- c("de Corazones", "de Diamantes", "de Picas", "de Tréboles")

# Creamos la combinatoria de cartas
combinatoria <- expand.grid(numero = numeros, palo = palos)

# Concatenamos vectores para tener nuestra combinación final
paste(combinatoria$numero, combinatoria$palo)
#>  [1] "As de Corazones"     "Dos de Corazones"    "Tres de Corazones"  
#>  [4] "Cuatro de Corazones" "Cinco de Corazones"  "Seis de Corazones"  
#>  [7] "Siete de Corazones"  "Ocho de Corazones"   "Nueve de Corazones" 
#> [10] "Diez de Corazones"   "Jack de Corazones"   "Reina de Corazones" 
#> [13] "Rey de Corazones"    "As de Diamantes"     "Dos de Diamantes"   
#> [16] "Tres de Diamantes"   "Cuatro de Diamantes" "Cinco de Diamantes" 
#> [19] "Seis de Diamantes"   "Siete de Diamantes"  "Ocho de Diamantes"  
#> [22] "Nueve de Diamantes"  "Diez de Diamantes"   "Jack de Diamantes"  
#> [25] "Reina de Diamantes"  "Rey de Diamantes"    "As de Picas"        
#> [28] "Dos de Picas"        "Tres de Picas"       "Cuatro de Picas"    
#> [31] "Cinco de Picas"      "Seis de Picas"       "Siete de Picas"     
#> [34] "Ocho de Picas"       "Nueve de Picas"      "Diez de Picas"      
#> [37] "Jack de Picas"       "Reina de Picas"      "Rey de Picas"       
#> [40] "As de Tréboles"      "Dos de Tréboles"     "Tres de Tréboles"   
#> [43] "Cuatro de Tréboles"  "Cinco de Tréboles"   "Seis de Tréboles"   
#> [46] "Siete de Tréboles"   "Ocho de Tréboles"    "Nueve de Tréboles"  
#> [49] "Diez de Tréboles"    "Jack de Tréboles"    "Reina de Tréboles"  
#> [52] "Rey de Tréboles"

Una vez creada nuestra baraja podemos calcular algunas probabilidades fácilmente con el vector creado.

Calculemos la probabilidad de que al escoger una carta ésta sea “Rey de Diamantes”:

O también podemos calcular la probabilidad de que al escoger una carta ésta sea alguna Reina:

5.3 Ejercicios

  1. Almacena en la variable prob la probabilidad de que al tirar un dado no te salga el número 1. Utilizando la variable prob, ahora calcula la probabilidad de que al tirar 3 veces seguidas, una tras otra, en ninguna de esas veces salga el número 1.

Solución

  1. Dada un recipiente que contiene 5 canicas azules, 3 amarillas y 4 grises. ¿Cuál es la probabilidad de que si escoges una canica al azar ésta sea azul?

Solución

Matemáticamente sería:

Dado el evento: \(X = canica\ elegida\ sea\ de\ color\ azul\):

\(P(X)=\frac{5}{5+3+4}=\frac{5}{12}=41.67\%\)

La probabilidad de que la canica sea azul es de 41.67%.

  1. ¿Cuál es la probabilidad de que al escoger una canica al azar del recipiente anterior ésta no sea de color azul?

Solución

La probabilidad es de 58.33%.

Matemáticamente sería:

Dado el evento \(X = canica\ elegida\ sea\ de\ color\ azul\):

\(P(\sim~X)=1-P(X)=1-\frac{5}{12}=1-41.67\%=58.33\%\)

  1. Ahora vamos a sacar primero una canica, colocarla fuera de la caja y sacar otra canica adicional de la caja. ¿Cuál es la probabilidad de que la primera sea azul y la segunda no sea azul?. Esta vez, en vez de crear el vector canicas, crea las variables numéricas: azul, amarillo y gris asigándole como valor el número de canicas. Luego calcula matemáticamente las probabilidades.

Solución

A esto se le llama muestreo sin reemplazamiento. Tenemos dos eventos, estamos sacando dos canicas. El segundo evento depende del primero. Estos dos eventos no son independientes uno del otro.

  1. Ahora repetiremos el experimento anterior, pero después de sacar la primera canica volvemos a colocarla en la caja y sacamos una canica más al azar. ¿Cuál es la probabilidad de que la primera canica sea azul y la segunda no sea azul? Modifica el código en R que creaste anteriormente para calcular esta probabilidad.

Solución

A esto se le llama muestreo con reemplazamiento. Tenemos dos eventos, estamos sacando dos canicas nuevamente. El segundo evento no depende del primero. Estos dos eventos son independientes.

5.4 Combinaciones y permutaciones

Algunas situaciones de probabilidad implican múltiples eventos. Cuando uno de los eventos afecta a otros, se llaman eventos dependientes. Por ejemplo, cuando objetos son escogidos de una lista o grupo y no son devueltos, la primera elección reduce las opciones para futuras elecciones.

Existen dos maneras de ordenar o combinar resultados de eventos dependientes. Las permutaciones son agrupaciones en las que importa el orden de los objetos. Las combinaciones son agrupaciones en las que el contenido importa pero el orden no.

Para ello vamos a utilizar el paquete gtools, el cual nos incluye librerías como gtools que nos provee intuitivas funcionalidades para trabajar con permutaciones y combinaciones.

5.4.1 Permutaciones

Importa el orden cuando calculamos, por ejemplo, los ganadores de una competencia. Supongamos que tenemos 10 estudiantes que están compitiendo en igualdad de condiciones por quién construye el modelo en machine learning más preciso.

Solo los top 3 recibirán el premio. En este caso el orden importa, entonces usaremos la función permutations(total, seleccion, data) donde el total me indica el tamaño del vector, seleccion indica el tamaño del resultado que quiero, y finalmente data es mi vector fuente.

Ya hemos calculado todos los resultados posibles. Podemos sobre este resultado calcular la probabilidad de que Fredy gane la competencia y que Pamela quede en segundo lugar.

5.4.2 Combinaciones

No importa el orden cuando, por ejemplo, formamos grupos de a 2 para que participen en la competencia.

Si ahora es un solo equipo el que va a ganar el premio, podríamos calcular la probabilidad de que el equipo conformado por Pamela y Enrique sean quienes ganen.

Si bien podemos obtener la probabilidad calculando todas las combinaciones, en R será muy frecuente utilizar Montecarlo para estimar la probabilidad por simulación. Para el caso anterior no tendríamos que generar todas las combinaciones, sino simplemente sacar una muestra de dos personas que serían los miembros del equipo ganador. Recordemos que hemos asumido que todos tienen igualdad de posibilidades de ganar.

Luego, tendríamos que replicar este experimento una y otra vez, almacenar los resultados del muestreo y calcular la proporción de cuántas veces el equipo ganador fue compuesto por Pamela y Enrique.

Nótese que, como vimos anteriormente, el valor converge conforme aumentamos la cantidad de veces que repetimos el experimento n. Hemos simulado repetir el experimento 10 mil veces. Sin embargo, ¿cuántas veces se necesitaría replicar el experimento para confiar en los resultados de la simulación?

5.5 Experimentos suficientes con Simulación de Montecarlo

Intuitivamente podemos indicar que a mayor cantidad de experimentos es más precisa la probabilidad estimada. Podemos, así, hacer varias simulaciones con diferente número de experimentos para cada simulación. De esta forma podríamos encontrar un número razonable de experimentos para nuestra simulación. Para ello, primero creemos un vector numérico donde se indique la cantidad de veces que vamos a simular el experimento. Nuestro vector contendrá los siguientes valores: 10, 20, 40, 80, 160,…, etc. Esto quiere decir que la primera vez simularemos 10 veces el experimento, la segunda 20 veces y así sucesivamente.

Luego, utilizamos el código que creamos para replicar el experimento para crear una función llamada probabilidad_por_muestra:

Ya tenemos una función que nos permite replicar el experimento cuantas veces querramos. Por ejemplo, en la sección anterior simulamos 10 mil experimentos. Ahora que tenemos creada la función haríamos:

Nuevamente, esta es una simulación. Así que cada vez que ejecutemos esa función la probabilidad variará al ser una muestra al azar.

Para aplicar una función sobre cada uno de los valores de un vector utilizamos la función sapply(vector, funcion) donde vector es el vector donde están los datos sobre los cuales quiero aplicar la función y funciones la función que quiero aplicar.

Esto nos da las probabilidades dependiendo del número de veces que repetimos el experimento. Ahora coloquemos estos resultados en un diagrama de dispersión para ver cómo converge

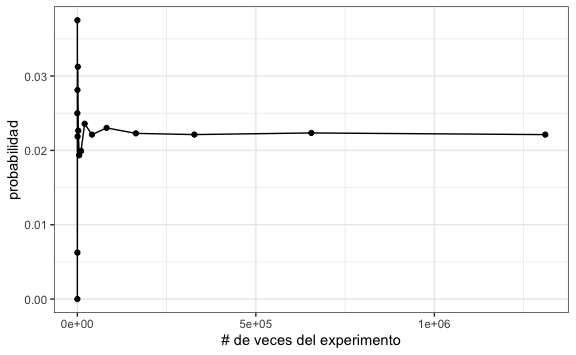
También podemos cambiar la escala para hacer un zoom a las probabilidades para los valores de número de experimentos más pequeños y agregar una línea de referencia con el valor de la probabilidad teórica calculada anteriormente:

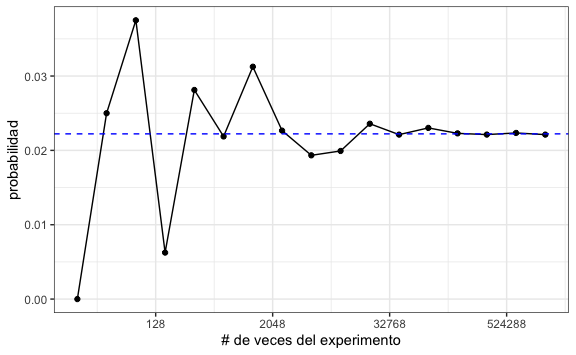
Observamos que, para este experimento, repitiendo el experimento 10 mil veces (eje-x = 3 porque es \(10^3\)) ya nos da una buena aproximación al valor real.

5.6 Caso: Cumpleaños en clases

Repasemos los conceptos aprendidos con otro ejemplo. En una clase de Data Science for Managers hay 50 estudiantes. Utilizando simulación de Montecarlo estimemos cuál es la probabilidad de qué hayan al menos dos personas que cumplan años el mismo día. (Obviemos a los que cumplen años el 29 de febrero).

Primero listemos todos los días del año disponible para cumpleaños:

Generemos una muestra aleatoria de 50 números del vector dias, pero ésta vez con reemplazo porque una persona podría tener el mismo día, y almacenémoslo en la variable colegas.

Para validar si alguno de los valores se repite usaremos la función duplicated() que nos valida si dentro del vector hay valores duplicados:

Finalmente, para determinar si hubo algún valor TRUE utilizamos la función any():

El resultado nos indica si es verdadero o no que hayan al menos dos personas que cumplan el mismo día años. Para estimar por simulación de Montecarlo cuál es la probabilidad tenemos que repetir el experimento muchas veces y sacar la proporción de cuántas veces nos sale como resultado TRUE.

Vemos que la probabilidad estimada es muy alta, arriba del 95%. ¿Qué pasaría si tengo un salón de 25 personas?

Para ello, modificamos el código anterior y creamos la variable clase que nos indicará el número de estudiantes en esa clase:

Creemos ahora la función calcula_probabilidad y estimemos usando esta función la probabilidad de encontrar al menos dos personas con el mismo día de cumpleaños en un salón de 25 personas. Ésta vez tenemos que especificar que el muestreo es con “reemplazo” porque por default la función sample() es “sin reemplazo”.

Finalmente, si ya tenemos una función que nos calcula en base al número de personas en un salón podemos crear un vector numérico con el total de personas de diferentes salones y luego aplicarle la función que hemos creado. El resultado lo podemos almacenar en la variable prob.

Así, si colocamos en un gráfico de dispersión podemos ver cómo incrementa la probabilidad conforme hay más estudiantes:

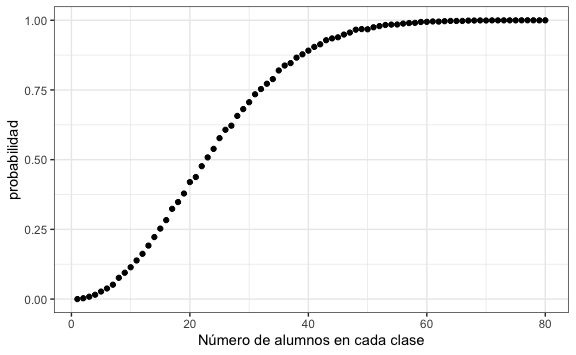
Ya podemos impresionar a nuestros amigos de distintos grupos diciéndoles que, si están en un salón de 60 personas, “les pueden apostar” que hay dos personas en ese salón que cumplen años el mismo día. No es definitiva, pero las chances están muy a nuestro favor.

5.7 Ejercicios

  1. Dos estudiantes del curso de Data Science con R, Alonso y Georgina, en sus ratos libres suelen jugar ajedrez. Dada la experiencia de Georgina, ella tiene 60% de ganar cada vez que juega con Alonso. Sin utilizar simulación de Montecarlo ¿Cuál es la probabilidad de que al jugar 4 veces seguidas, Alonso haya ganado al menos una vez.

Solución

Calcular la probabilidad de que Alonso haya ganado al menos una vez es el complemento de la probabilidad de que Georgina haya ganado todas las 4 veces. Así, calcularemos primero la probabilidad de que Georgina haya ganado siempre y luego calculamos el complemento.

  1. Estima la probabilidad anterior utilizando simulación de Montecarlo. Utiliza el siguiente código para generar una muestra de 4 juegos, donde Alonso tiene una probabilidad de 60% de perder ante Georgina.

Solución

  1. En el ejercicio anterior usamos como probabilidad de que Alonso gane como 40%. Ahora, crea la función probabilidad_de_ganar que tome como input la probabilidad p de que Alonso gane. Luego, asigna esta secuencia seq(0.4, 0.95, 0.025) en un vector p para, finalmente, aplicar la función creada a cada valor del vector p y almacena el resultado en la variable prob. Reporta un diagrama de dispersión del vector p en el eje-x y del vector prob en el eje-y

Solución

5.8 Ejercicio integrador

Vamos a resolver juntos este ejercicio que integra todo lo que hemos aprendido en este capítulo, llamado el problema de Monty Hall.

5.8.1 Problema de Monty Hall

Monty Hall era un presentador de TV que hizo famoso un concurso en su show el cual vamos a replicar a continuación. Tenemos tres puertas frente a nosotros:

Detrás de una de estas puertas hay un auto cero kilómetros, mientras que en las otras dos hay una cabra. Nosotros, como participantes del concurso, tenemos que elegir juntos qué puerta abrir. Lo que haya detrás será nuestro.

Supongamos que hemos elegido la puerta número 2. Una vez anuncias nuestra elección, Monty Hall nos dice que él nos va a ayudar y abrirá una puerta por nosotros ahora mismo. Él abre una de las otras puertas y resulta que hay una cabra en la puerta 3 que abrió.

Monty Hall nos pregunta:

Les voy a dar una oportunidad de cambiar de puerta y esa será su elección final, ¿Cambiarían de puerta o se quedan con la puerta elegida al inicio?

Intuitivamente sabíamos que, cuando todas las puertas estaban cerradas, el auto está en una de 3 las puertas. La probabilidad de ganar sería \(\frac{1}{3} = 0.3333\) así que daba lo mismo cuál puerta elegir. Pero cuando abre la puerta número tres nos brinda información y lo primero que deberíamos de preguntarnos es si las probabilidades se han visto afectadas o no. Si bien este es un ejercicio de matemática avanzada usando el cambio de variable, podemos ejecutar una simulación de Montecarlo para estimar las probabilidades y resolverlo sin usar casi ninguna fórmula matemática.

Comencemos simulando el experimento. Al inicio teníamos tres puertas, puerta 1, 2 y 3. Crearemos la variable puertas.

Luego, sabemos que detrás de las puertas hay un auto y dos cabras distribuídos aleatoriamente. Usaremos la función sample para ordernarlos de forma aleatoria.

Como Monty Hall sabe dónde está el premio. Vamos a crear una variable puerta_premio donde almacenaremos donde está el auto.

Ahora escogemos una puerta aleatoriamente y almacenamos nuestro resultado en la variable eleccion.

Dado que ya tenemos mostrada la puerta elegida simularemos el que Monty Hall elija la puerta a abrir. Como él es el presentador elegirá cualquier puerta que no sea la puerta donde está el premio o tu puerta.

Finalmente, vamos a poner todo el código junto y en la última línea agregamos la comparación de si la puerta del premio coincide con nuestra elección. En esta oportunidad vamos a elegir no cambiar de puerta, así que nuestra elección no varía.

Ya con nuesro experimento creado vamos a simular qué pasaría si nos quedamos con la elección y qué pasaría si la cambiamos.

5.8.1.1 Quedarse con la puerta elegida

Repliquemos unas 10 mil veces para ver la proporción de veces que ganaríamos si nos quedamos con nuestra puerta.

Vemos que la probabilidad obtenida simulación de Montecarlo es una estimación muy cercana a la probabilidad que intuitivamente habíamos calculado. Es decir, si mantenemos nuestra elección de la puerta que elegimos tenemos un 33.33% de probabilidad de ganar.

Pero, ¿qué pasa si cambiamos de puerta? ¿la probabilidad de ganar es la misma?

5.8.1.2 Cambiar de puerta

Vamos a utilizar el código y lo modificaremos creando la variable nueva_eleccion para hacer el cambio de puerta.

Como vemos, cambiar la puerta en este show nos daba una probabilidad de 66.66% de ganar, mientras que mantener nuestra elección solo 33.33%.

Puede sonar contraintuitivo, pero estadísticamente hablando es mejor cambiar de puerta en vez de confiar en nuestra suerte y mantener la elección inicial.