Capítulo 7 Inferencia estadística

Inferir significa extraer una conclusión a partir de hechos generales o particulares. La inferencia estadística es un conjunto de métodos y técnicas que permiten deducir características de una población utilizando datos de una muestra aleatoria. El método que más vamos a utilizar para inferir es el método de estimación de parámetros.

Estimamos parámetros de una población a partir de una muestra porque muy pocas veces vamos a poder tener acceso a toda la data de la población. Tal es el caso de las encuestas de elecciones, estudios de enfermedades, etc.

Recordemos previamente algunos conceptos como valor esperado, error estándar, entre otros, que nos será útiles para realizar inferencias.

7.1 Valor esperado

Utilicemos el siguiente caso para comprender intuitivamente este conceptos.

Nos han contratado en un casino para analizar si es razonable instalar una ruleta con 37 valores que van del 0 al 36. La casa quiere abrir el juego con una oferta especial si la bola cae en el 0 o 21 pagando 10 a 1. Esto quiere decir que si un jugador juega y gana le pagamos 10 soles y si pierde él nos pagaría 1 sol.

Con lo aprendido hasta ahora podemos simular nuestro juego con los datos del caso. Tenemos 37 valores, de los cuales en 2 de ellos le dan a un jugador una ganancia de +10 o una pérdida -1. Definamos también a prob_gana como la probabilidad de que gane un jugador.

La distribución de esta variable es sencilla dado que solo puede tomar dos valores: 10 o -1. Cuando simulamos un número de juegos muy grande se puede ver cómo se distribuye de acuerdo a la probabilidad indicada de ganar y de perder.

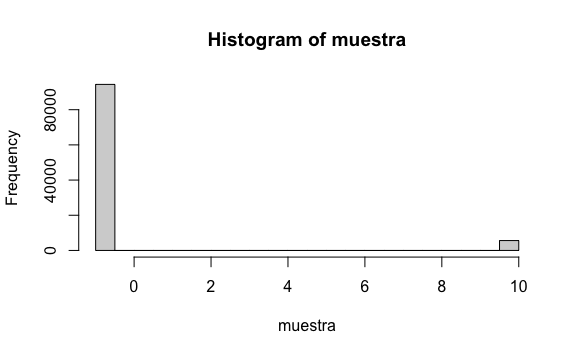
Hemos venido usado la simulación de Montecarlo para estimar cuál sería la media de los resultados del juego en la vida real.

Además, hemos visto que, mientras más crece la muestra, nuestra media en la simulación de montecarlo converge a un valor, en este caso la probabilidad de ganar en la ruleta. Ese valor al que converge le llamaremos valor esperado, la cual como su nombre lo indica será el valor que esperamos obtener en la realidad. Mientras más crece el tamaño de la muestra más converge nuestra media muestral a este valor esperado. La notación que usaremos será \(E[X]\).

Cuando solo hay dos posibles resultados \(a\) y \(b\) con proporciones \(p\) y \(1-p\) respectivamente el valor esperado lo calcularemos usando esta fórmula:

\(E[X] = ap + b(1-p)\)

Anteriormente habíamos calculado la media utilizando la simulación de Montecarlo. Si lo comparamos con el valor esperado vemos cómo ambos números son aproximadamente el mismo, como predice la teoría.

Regresando a la simulación de los juegos de la ruleta, una sola persona no juega tantas veces. Cada persona juega unas 40 veces al día a la ruleta. Así, podemos generar 40 juegos que un jugador aleatorio podría jugar y encontrar cuánto es lo que ganaría:

Finalmente, no solo una persona jugará. Repliquemos esta muestra unas 100,000 veces para simular la cantidad de jugadores que tendríamos en un trimestre.

Hasta acá hemos hecho lo mismo que hemos aprendido en los capítulos anteriores. Sin embargo, también podríamos ver cómo están distribuidas las ganancias de los jugadores. Y para ello basta crear un histograma del resultado.

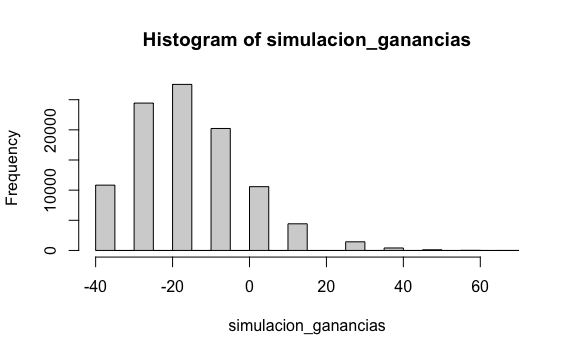
No es una coinciencia que si creamos un histograma con todas las ganancias de todos los jugadores el resultado se vea como una distribución normal. De hecho, ese fue el principal planteamiento que George Pólya hizo en 1920 cuando presentó su Teorema del Límite Central.

7.2 Teorema del Límite Central

El Teorema del Límite Central nos indica que si tomamos varias muestras del mismo tamaño \(n\) y en cada muestra sumamos los valores dentro de cada muestra obtendremos un valor \(S\) (la suma) entonces encontraremos que su distribución se aproxima bien a una curva normal.

Si replicamos este lenguaje a nuestro ejemplo sería: El teorema del límite central nos indica que si tomamos muestras de 40 jugadas para cada jugador y luego calculamos para cada jugador el total que ganó, entonces encontraremos que la distribución de la cantidad ganada por muchos jugadores se aproxima a una distribución normal.

Como se trata de una nueva distribución, podemos calcular su media y su desviación estándar. Al tratarse de muestras usaremos el término aprendido valor esperado de la suma para referirnos a la media de la muestra y agregaremos el término de error estándar de la suma para referirnos a la desviación estándar de la muestra

Esta sería la fórmula para calcular el valor esperado de la suma:

\(E[S_n] = n (ap+b(1-p))\)

Y para calcular el error estándar de la suma usaremos la siguiente fórmula:

\(SE[S_n]=\sqrt{n}\ |a-b|\ \sqrt{p(1-p)}\)

Con estos dos datos teóricos, el valor esperado y el error estándar, podemos graficar la curva normal de la suma de ganancias de nuestro juego.

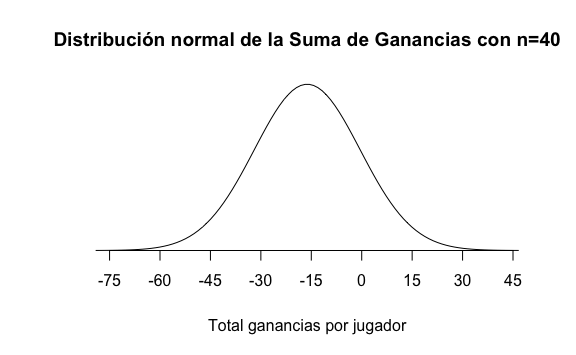
¿Esto qué quiere decir? Que si teóricamente ya podemos graficar la curva normal entonces también podemos calcular la probabilidad de que la suma sea mayor o menor que algún valor. Ésta es la principal ventaja del Teorema del límite central puesto que podemos calcular probabilidades de la población utilizando esta aproximación y los datos de una sola muestra.

Por ejemplo, si queremos saber ¿cuál es la probabilidad de que un jugador gane dinero luego de jugar 40 veces en la ruleta tendríamos que calcular la probabilidad de que \(S\) sea mayor que cero, representada por el área sombreada en azul:

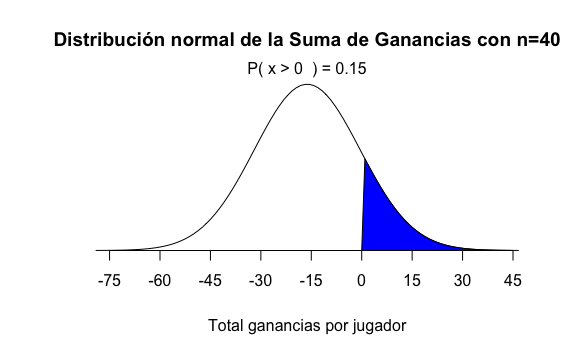
Para hacer este cálculo en R usaríamos la función pnorm:

Validemos que la simulación de Montecarlo se aproxima a este valor teórico que acabamos de calcular:

Hemos utilizado dos formas de estimar la probabilidad, la estimación teórica utilizando el teorema del límite central y la simulación de Montecarlo. Estos dos números se aproximan bastante a la probabilidad real. En ambos casos, mientras más grande sea la muestra más razonable será nuestra estimación.

Por otro lado, lo mismo ocurre si quisiéramos analizar el promedio y no la suma de las ganancias. Pero para el caso del promedio usaremos las siguientes fórmulas:

  1. Valor esperado del promedio: \(E[\overline{X}]=ap+b(1-p)\).
  2. Error estándar del promedio: \(SE[\overline{X}]=|a-b|\sqrt{\frac{p(1-p) }{n}}\).

7.3 Ejercicios

El examen de admisión de la Univ. Nacional de San Marcos consta de 100 preguntas de opción múltiple (A, B, C, D, E) con un valor de 20 puntos por cada pregunta correcta y 1.125 por cada respuesta equivocada. Queremos analizar qué pasaría si un estudiante responde todas las 100 preguntas al azar y si hay chances de conseguir vacante alguna sabiendo que se necesita mínimo 900 puntos para ingresar a alguna carrera.

  1. ¿Cuál es el valor esperado de los puntos recibidos al adivinar una pregunta?

Solución

  1. ¿Cuál es el valor esperado de adivinar las 100 preguntas?

Solución

  1. ¿Cuál es el error estándar de adivinar de adivinar las 100 preguntas?

Solución

  1. Utilizando el teorema del límite central, ¿Cuál es la probabilidad que un estudiante obtenga más de 900 puntos al marcar todas las respuestas al azar?

Solución

Esto quiere decir que la probabilidad de que un estudiante obtenga el puntaje mínimo adivinando todas las preguntas es de: 0.0000000000014525.

Conclusión: estudiemos antes de dar el examen. No es razonable dar el examen al azar y marcar al azar.

Recordemos que e-n es la representación de \(10^{-n}\).

  1. Usando simulación de Montecarlo para los 22,000 postulantes que postulan cada vez, calcula la probabilidad de que un estudiante obtenga más de 900 puntos al marcar todas las respuestas al azar.

Solución

Vemos que la simulación nos arroja prácticamente el mismo resultado. Prácticamente no existen posibilidades de ingresar a la UNMSM adivinando las respuestas.

7.4 Método de estimación de parámetros

Hasta el momento, usando simulación de Montecarlo hemos construido muestras aleatoriamente, pero sabiendo la probabilidad de ocurrencia. Sin embargo, no siempre vamos a saber la proporción previamente. Si tenemos, por ejemplo, una población y queremos saber cuántos han sido infectados por Covid-19, no podemos testear a todos. O si tenemos el total de electores a una elección, no podemos encuestar a todos para saber quién ganaría. No solo es muy costoso, sino que nos tomaría mucho tiempo.

El método de estimación de parámetros es el procedimiento utilizado para conocer las características de un parámetro poblacional, a partir del conocimiento de una muestra de \(n\) encuestados

Analizaremos este siguiente caso.

Tenemos dos partidos políticos: Azul y Rojo. No conocemos cuánto es el total de la población, ni la proporción que votará por uno u otro partido. Lo único que podemos hacer es hacer encuestas de intención de voto.

Por ejemplo, éstas serían los resultados de la encuesta a una muestra aleatoria a 10 personas:

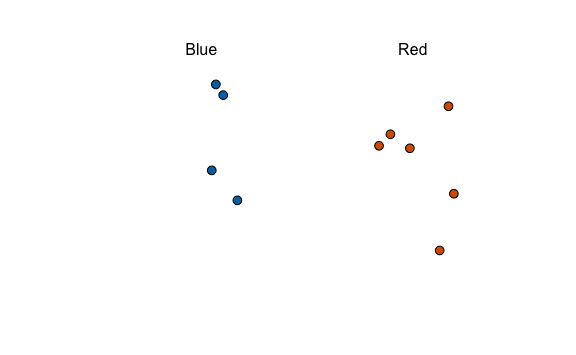
Intuitivamente sabemos que no podemos deducir qué partido ganará dado que la muestra es muy pequeña. Para saber qué partido ganará necesitamos estimar lo más preciso posible el parámetro \(p\) que representa a la proporción de votantes del Partido Azul en la población y el parámetro \(1-p\) que representa la proporción de votantes del partido Rojo.

Haciendo algunas transformaciones matemáticas a nuestras estimaciones teóricas vistas anteriormente y definiendo \(a=1\) como valor si votan Azul y \(b=0\) si no votan por Azul, podemos obtener las siguientes estimaciones teóricas para este caso:

  1. Valor esperado de cada voto:

\(E[X]=p\)

Vemos que el valor que esperamos obtener por voto \(E[X]\) coincide con el parámetro \(p\) que estamos buscando.

  1. Valor esperado del promedio de votos:

\(E[\overline{X}]=p\)

Si hacemos múltiples encuestas, todas de \(n\) encuestados y calculamos la media \(\overline{X}\) de cada muestra, éstas muestras seguirán una distribución normal con un valor esperado \(E[\overline{X}]\) el cual, como vemos, coincide con el parámetro \(p\) que estamos estimando.

  1. Error estándar del promedio de votos:

\(SE[\overline{X}]=\sqrt{\frac{p(1-p) }{n}}\)

De la misma forma que en el punto anterior, las múltiples encuestas generan múltiples medias sobre las cuales se puede calcular el error estándar \(SE[\overline{X}]\) que dependerá del tamaño \(n\) de encuestados.

El valor esperado del promedio \(E[\overline{X}]\), fórmula 2, es teóricamente igual al parámetro \(p\) que estamos buscando estimar. Sin embargo, sin saber cuánto es \(p\) tendríamos que tener múltiples muestras de \(n\) encuestados, luego calcular la media para cada caso \(\overline{X}\) y finalmente calcular el promedio de estos valores. Esto es muy costoso, así que buscaremos de otra forma estimar \(E[\overline{X}]\).

Dado que no tenemos hasta el momento cómo estimar \(E[\overline{X}]\), y dado que sabemos que \(E[\overline{X}]=p\) entonces podríamos darle varios valores a \(p\) y ver el impacto en el error estándar del promedio que sabemos que también depende de \(p\).

Generemos, primero, una secuencia del parámetro \(p\), desde 0% hasta 100%, 100 diferentes valores:

Pensar en 100 valores diferentes de \(p\) sería como pensar en 100 elecciones diferentes donde el partido Azul y el rojo tienen participación, como la elección para alcaldes a nivel nacional. En algunos distritos pierde el candidato del partido Azul con 0%, en otros empate al 50% y en otros gana rotundamente con 100% de los votos.

Intuitivamente sabemos que si nuestra proporción real fuese de \(p=80\%\) para el partido Azul, es decir que 8 de cada 0 votarán Azul, entonces es muy probable que en cada encuesta que tomemos encontraremos que en ese distrito que el partido Azul tiene la mayoría de votos. Esto se predice con la fórmula antes vista y además incluye el tamaño de la encuesta \(n\) como parte del cálculo:

\(SE[\overline{X}]=\sqrt{\frac{p(1-p) }{n}}\)

Dicho ello, regresemos a nuestro vector p que contiene varios valores del parámetro \(p\). Sobre esos valores podemos calcular qué pasaría si encuestamos grupos de 20 personas. Sabiendo el tamaño de la muestra podemos calcular el error estándar del promedio para cada uno de los valores de \(p\):

Ahora generemos un gráfico de dispersión tanto de los diferentes valores de \(p\) como de los errores estándar para cada \(p\).

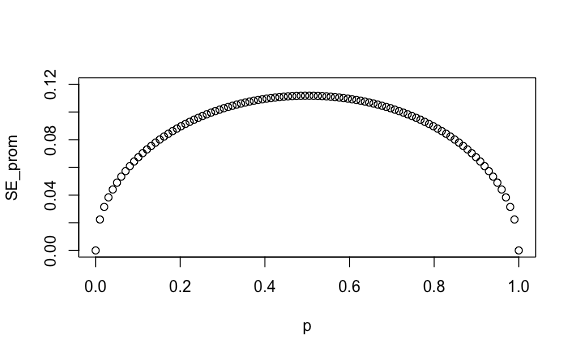
Así, vemos cómo podemos obtener diferentes errores estándar del promedio para distintos valores de \(p\).

Intuitivamente teníamos la noción de qué pasaría ante un \(p=80\%\). Ahora en el gráfico lo vemos mejor. Si la intención real de voto fuese 80% en ese distrito entonces al tomar varias encuestas y ver los resultados de cada encuesta obtendríamos como valor esperado 80% y como error estándar 8.8% o 0.088 como se ve en la gráfica resaltado en azul:

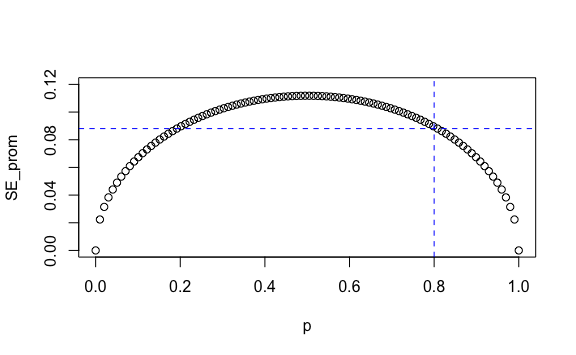
Con estos valores de \(E[\overline{X}]=p=80\%\) y \(SE[\overline{X}]=8.8\%\) de error estándar podemos calcular un rango de un error estándar alrededor de \(80\%\), el cual iría desde \(71.2\%\) hasta \(88.8\%\) y luego cálcular cuál sería la probabilidad de que la media \(\overline{X}\) encontrada en una de las encuestas caiga en este rango. Visualmente sería:

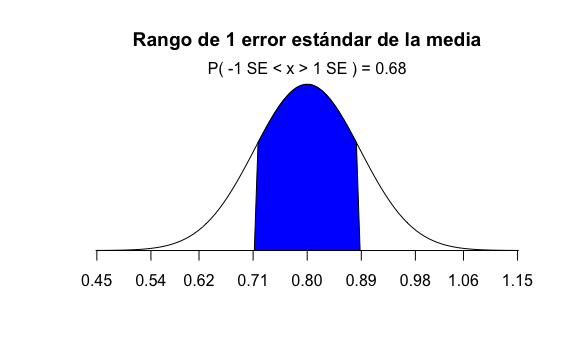
En R, calcular la probabilidad de que un dato se encuentren en el rango de 1 error estándar sería:

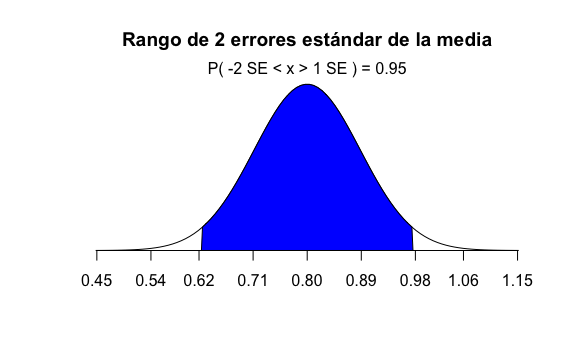
Podemos ampliar a tener un rango mayor de 2 errores estándares alrededor de \(80\%\) e incrementar nuestra probabilidad:

En R sería:

La probabilidad aumenta a 95%, sin embargo ¿cómo interpretamos esto?. No hemos calculado siquiera el valor real de la media \(\overline{X}\) de alguna encuesta.

Sencillo, esto quiere decir que, teóricamente, hay un 95% de probabilidad de que la media \(\overline{X}\) que encontremos en cada encuesta esté en el rango de 62% a 98%, dos errores estándar alrededor de \(80\%\). El 95% de las veces en el peor de los casos, en una encuesta a 20 personas, el partido Azul obtendría 62% y en el mejor de los casos 98%, con lo que podríamos predecir que ganará el partido Azul. ¿O no?

Debería hacernos ruido varias cosas hasta el momento. Primero, el rango tan grande, desde 62% a 98%. Segundo, hemos asumido un escenario: que la intención de voto Azul se conociese y fuese de 80%. Es decir, hemos asumido \(p=80\%\) que nos permitió calcular \(E[\overline{X}]=80\%\) y colocar ese valor al centro de la normal. Sin embargo, \(p\) es desconocido y es precisamente lo que intentamos estimar.

Si, por el contrario, el resultado estuviese más apretado, por ejemplo \(p=55\%\), no nos serviría un rango tan amplio. Veamos cómo sería:

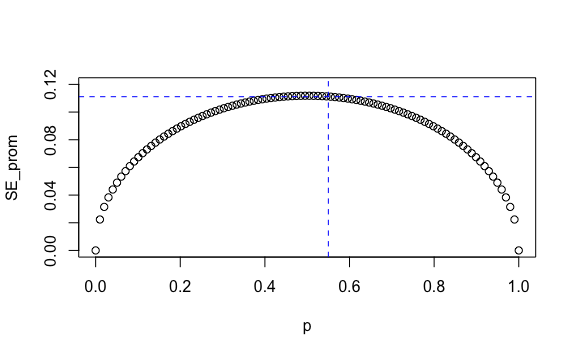
Si la intención real de voto real fuese \(55\%\) tendríamos un valor esperado del promedio \(E[\overline{X}]=p=55\%\) y un correspondiente error estándar del promedio \(SE[\overline{X}]=11\%\). Nuevamente, por Teorema del Límite Central podemos calcular un rango de dos errores estándar alrededor de \(55\%\):

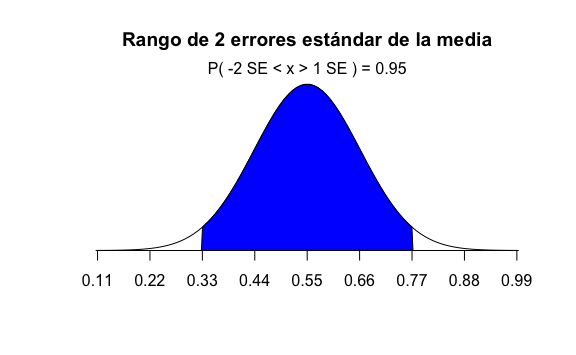
El cálculo de la probabilidad de estar en ese rango en R sería el mismo porque seguimos en el rango de 2 errores estándar. Por ende la probabilidad sería la misma.

Sin embargo, lo que sí cambia es el rango. Ahora el rango va desde 32.8% hasta 77.2%, dos errores estándar alrededor del valor esperado del promedio \(E[\overline{X}]\). Si bien la probabilidad sigue siendo 95%, eso no nos ayuda en nada esta vez porque hay un 95% de que lo que encontremos en nuestra muestra sea un valor entre 33% y 77%. Algunas muestras de encuestas nos darán 33% de votos para el Azul y otras muestras 77%.

Y es que el problema radica en la cantidad de muestras tomadas \(n\). Si vemos nuevamente la fórmula vemos cómo influye \(n\) en el resultado.

\(SE[\overline{X}]=\sqrt{\frac{p(1-p) }{n}}\)

Incrementemos entonces nuestros número de encuestados a 500:

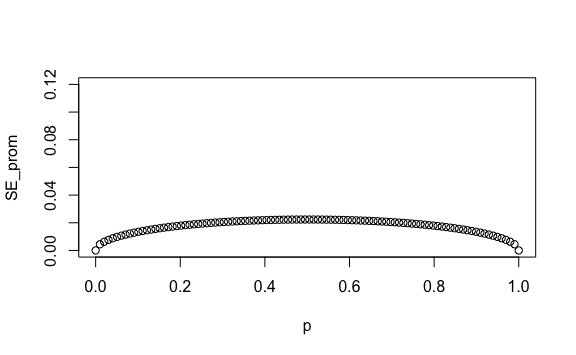
Esta muestra nos da errores estándar más pequeños. Por ejemplo, si la proporción real de votantes del partido Azul fuese \(p=55\%\) tendríamos \(E[\overline{X}]=p=55\%\) y un \(SE[\overline{X}]=2.2\%\):

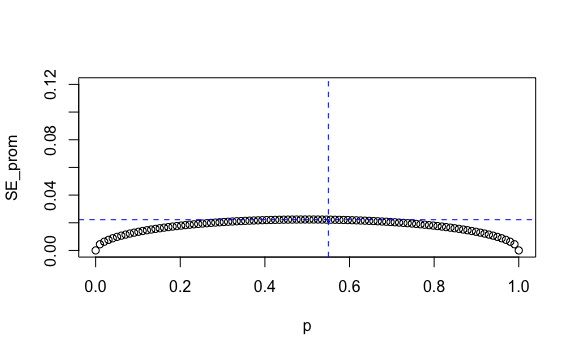
Si ahora calculamos un rango de dos errores estándar alrededor de \(55\%\) tendríamos un rango que va desde \(50.6\%\) hasta \(59.4\%\). Nuevamente, la interpretación es que la media que encontremos en nuestra encuesta aleatoria tiene un 95% de probabilidad de estar en ese rango.

Vemos pues que esta predicción teórica, el error estándar, se hace más pequeño conforme incrementa el tamaño de la muestra \(n\) y a su vez depende de la probabilidad de la población \(p\) que no conocemos. Es más, con un valor real de \(p=0.5\), (50%), tenemos el máximo valor del error estándar que podemos obtener. Así, si fijamos \(p\) en 50%, que sería el extremo de los casos, un empate, podemos calcular cómo cambia el valor del error estándar del promedio de acuerdo al tamaño de la muestra:

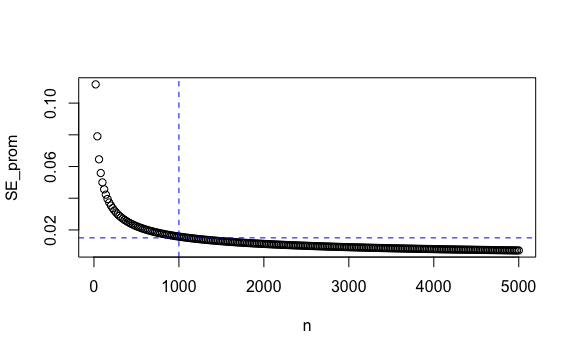
Una muestra de 1,000 personas, por ejemplo, nos genera un error estándar máximo de 0.015 o 1.5%.

7.4.1 Margen de error

Como ya hemos visto, podríamos considerar un rango de 1 error estándar o 2 errores estándar alrededor de \(E[\overline{X}]\) y calcular la probabilidad de que nuestra media muestral \(\overline{X}\) esté en ese rango. O lo que es matemáticamente lo mismo, podríamos decir que si construimos un rango de 1 o 2 errores estándar alrededor de nuestra media muestral \(\overline{X}\) hay una determinada probabilidad de que en ese rango se incluya el valor esperado \(E[\overline{X}]\) que es, por fórmula igual a \(p\), el valor que queremos estimar.

Es crucial entonces calcular el error estándar del promedio \(SE[\overline{X}]\), pero nos vemos limitados porque depende de \(p\).

Existe otra forma de calcular \(SE[\overline{X}]\) sin utilizar \(p\) y es conocida como el error estándar de estimación \(\hat{SE}[\overline{X}]\). Para ello usaremos la siguiente fórmula:

\(\hat{SE}[\overline{X}]=\sqrt{\frac{\overline{X}(1-\overline{X})}{n}}\)

Donde, como ya sabemos, \(\overline{X}\) es la media de nuestra muestra o media muestral. Para nuestro caso ejemplo, es el porcentaje que obtuvo el partido Azul en la encueta que realizamos.

Ahora que tenemos la media muestral \(\overline{X}\) y ya podemos calcular el error estándar de estimación \(\hat{SE}[\overline{X}]\) podemos empezar a construir rangos alrededor de \(\overline{X}\) que incrementen la probabbilidad de encontrar \(p\).

Para hacerlo más sencilla la comunicación, usaremos por convención la notación margen de error para indicar que vamos a tomar un rango de 2 errores estándar de estimación.

Por ejemplo, tenemos una muestra de 1100 personas y luego de revisar los resultados de la encuesta tenemos una media muestral de \(\overline{X}=56\%\) para el partido Azul. Con esto podemos estimar el error estándar de estimación \(\hat{SE}[\overline{X}]\) con la fórmula que acabamos de describir y finalmente calcular el margen de error.

Con esto tendríamos que de una muestra de 1100 personas, hemos estimado 56% de intención de voto para el partido Azul con un margen de error de \(+- 2.99\%\).

Finalmente, veamos ejemplos de las diferentes encuestas realizadas en Abril e inicios de Mayo del 2020 para medir las intenciones de voto en EEUU.

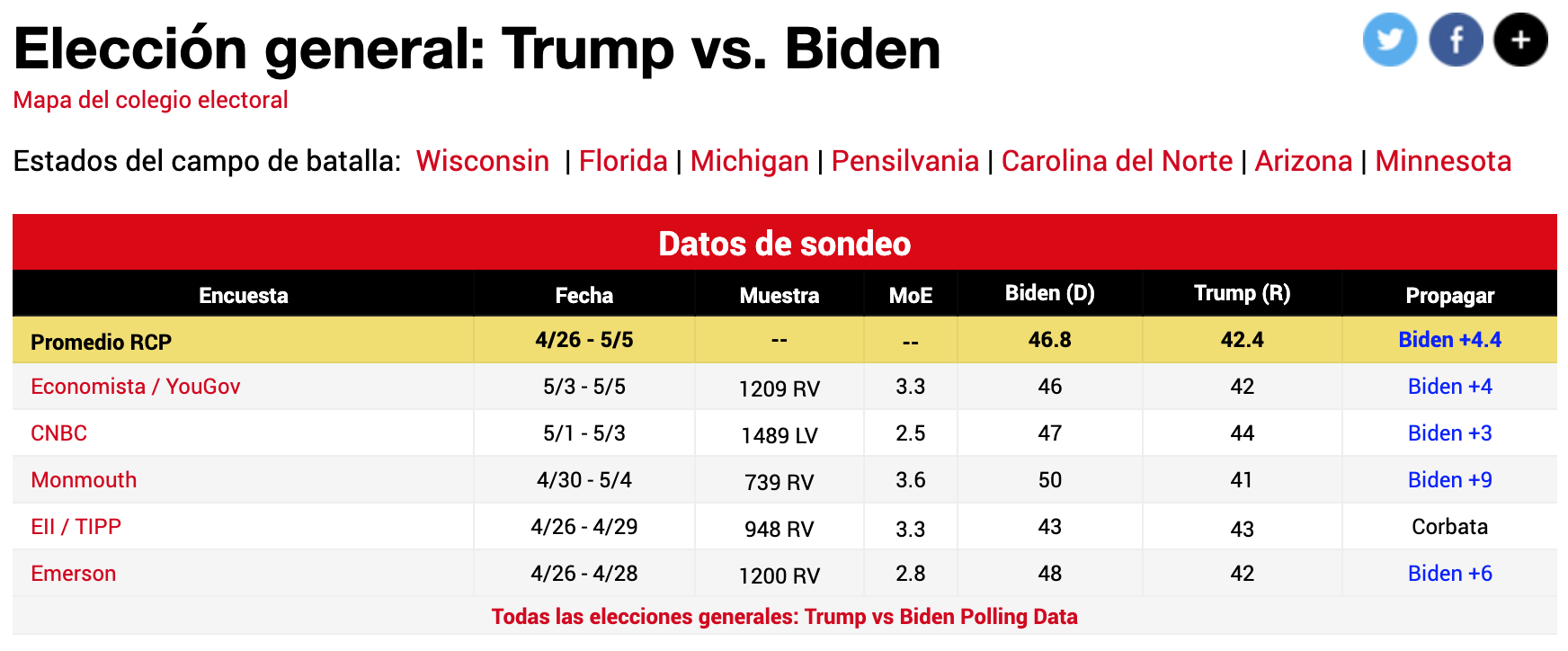
Vemos como columnas:

  • Encuesta: Empresa encuestadora que realizó el estudio
  • Fecha: Fecha de realización de la encuesta
  • Muestra: Cantidad de encuestados que varía por encuestadora
  • MoE: Margen de error
  • Candidatos: Cantidados a la presidencia. Sus porcentajes no suman 100% porque se omiten los blancos y nulos.
  • Propagación: Este es el Spread, la estimación de por cuánto gana un candidato al otro.

Si, por otro lado, nos preguntamos por qué no se hacen encuestas más grandes, por ejemplo 50,000 personas, el motivo es que:

  1. El costo de hacer encuestas a 50 mil personas es muy costoso.
  2. La estimación de parámetros es una predicción teórica, si damos un margen de error muy pequeño nuestros resultados podrían ser malinterpretados como verdades absolutas cuando sabemos que: 2.1 Toda persona puede cambiar su opinión y no estamos más que tomando una foto del momento. 2.2 Por más esfuerzo que se coloque ninguna encuesta es totalmente aleatoria o no se hacen en zonas rurales. 2.3 Podríamos encuestar personas que dicen que irán a votar, pero finalmente no lo harán, etc.

7.4.2 Intervalos de confianza

Los intervalos de confianza son un muy útil concepto ampliamente utilizado por los Data Scientists. Sin embargo, no es más que otra forma de expresar lo que ya hemos aprendido hasta el momento.

Y es que un intervalo de confianza del 95% nos indica que hay un 95% de probabilidad de que en el intervalo que generemos se incluya al parámetro \(p\) que queremos estimar. Esto no es más que otra forma de indicar que tenemos que construir un intervalo considerando el margen de error, es decir dos errores estándar alrededor de nuestra media muestral.

Para la muestra de 1100 personas que vimos en la sección anterior, reportamos un estimado de 56% con un margen de error de \(+- 2.99\%\).

Si ahora queremos utilizar intervalos de confianza en nuestro lenguaje diríamos: Estimamos un 56% para el partido Azul con un intervalo de confianza del 95%. Este intervalo de confianza va desde 53% hasta 59%.

7.5 Estimación del spread

Si bien estamos interesados en estimar la proporción que obtendría el partido Azul \(p\), algunas veces es más útil el conocer la diferencia (por cuánto es lo que gana/pierde). Por ejemplo, cuando tenemos dos partidos en segunda vuelta de elecciones no solo tenemos votos para Azul y Rojo, sino también blanco/viciado. Además, en elecciones regulares tenemos más de una encuestadora haciendo varias encuestas. Entonces una podría dar 45% para Azul, 41% para el Rojo. Mientras que otra puede dar 41% para Azul y 38% para el Rojo, etc. Si comparamos encuestas, más que saber el porcentaje exacto no es más útil saber por cuánto gana el partido azul, ya que si vemos que en todas, por ejemplo gana por 4%, con un error estándar pequeñísimo, entonces no importaría mucho \(p\). Solo con el dato de la diferencia podríamos tomar tener una idea de quién ganará.

A esta diferencia se le llama spread. Habíamos definido que la intención de votos para el partido Azul era \(p\) y para el partido rojo \(1-p\). Entonces lo que esperaríamos obtener para la diferencia sería \(p - (1-p)\), es decir \(2p - 1\).

Error estándar del spread:

\(SE[spread]=2\sqrt{\frac{p(1-p) }{n}}\)

Vemos que el error estándar es dos veces el error estándar del promedio, que depende de \(p\), y ya hemos encontrado anteriormente una estimación para no depender de \(p\) sino de la media de nuestra muestra. Así que utilizaremos:

\(\hat{SE[spread]}=2\sqrt{\frac{\overline{X}(1-\overline{X}) }{n}}\)

Veamos con un ejemplo estos conceptos. Estudiemos las elecciones de Estados Unidos del 2016. En este caso tenemos múltiples casas encuestadoras (pollster en inglés), realizando múltiples encuestas meses previos a elecciones, y principalmente dos partidos compitiendo a presidente.

Vamos a utilizar el data frame polls_us_election_2016 incluido en la librería dslabs que incluye data de múltiples encuestas realizadas para las elecciones del 2016 en EEUU entre Hillary Clinton y Donald Trump. Lo primero que haremos es explorar la data:

Como vemos, no tenemos el error estándar, ni el intervalo de confianza. Así que procederemos a hacer algunas mutaciones aplicando las fórmulas hasta el momento aprendidas enfocándonos en la intención de votos para Hillary Clinton.

Por ejemplo, IPSOS en una encuesta que publicó el 06/11/16 estimó 42% de intención de voto para Clinton con un intervalo de confianza al 95% en un rango que va desde 39.89% hasta 44.10%.

¿Este dato quiere decir que estimaron que perdería? No, dado que en este caso estamos usando datos reales no va a sumar 100% la proporción de votos de Clinton con los de Trump. De hecho, el día de la elección real Clinton obtuvo 48.2% y Trump 46.1% del total de votos emitidos. Es decir \(p\) real fue 48.2%.

Lo que sí podríamos calcular es cuántas de estas encuestadoras acertaron en su estimación. Es decir, si en sus intervalos de confianza está el \(p=48.2\%\) que finalmente obtuvo Clinton. Para ello, agregaremos una columna acertaron con la validación de si está en el intervalo de confianza y luego usamos summarize() para calcular el porcentaje de encuestas que acertaron.

Solo el 28% de las encuestas publicadas publicaron intervalos de confianza que incluían a \(p\). Esto, entre otras muchas razones, porque al inicio hay muchos más indecisos que finalmente se animan en las últimas semanas.

Analicemos ahora cuántas acertaron en el spread. Podría ser que por más que no estimaron exacto el \(p\) la diferencia sí se mantuvo a lo largo del tiempo. Para ello, agregemos a nuestras encuestas la columna spread con la diferencia de votos:

Y ahora vamos a hacer un artificio calculando el spread de nuestra muestra:

\(spread=2*\overline{X}-1\)

Podemos transformar esta fórmula:

\(spread-1=2*\overline{X}\)

\(\frac{spread-1}{2}=\overline{X}\)

O lo que es lo mismo:

\(\overline{X}=\frac{spread-1}{2}\)

Esta fórmula nos da una aproximación de cuánto sería el \(\overline{X}\) transformado a una escala del 0 al 100%. Con ello, calculemos el error estándar y el intervalo de confianza:

Ahora calculemos cuántas de estas encuestadoras acertaron en su estimación. Es decir, si en sus intervalos de confianza está el valor real del \(spread=48.2\%-46.1\%=2.1\%\) que finalmente obtuvo Clinton de spread. Para ello, agregaremos la columna acertaron y luego summarize().

En este caso vemos cómo 67.3% de las veces las encuestas estimaron correctamente la diferencia de votos favorables para Clinton.

Como aclaración, recordatorio final de este caso, aun cuando Clinton obtuvo más votos no ganó las elecciones porque el sistema de EEUU es diferente y no necesariamente si ganas en votos obtienes la presidencia.

7.6 Estimaciones fuera de encuestas de elecciones

Hemos utilizado encuestas de elecciones para entender los conceptos de inferencia estadística. Sin embargo, la mayoría de Data Scientists no están relacionados con cálculos de estimaciones de intención de votos. Eso no quiere decir que no usaremos esos conceptos. El teorema del límite central no solo funciona en encuestas de elecciones. Lo que quiere decir es que utilizaremos algunas fórmulas ligeramente diferentes que se aplican a más casos de la vida cotidiana.

De lo que hemos aprendido hasta el momento el principal cambio es la fórmula para calcular el error estándar. Utilizaremos en su lugar la desviación estándar \(\sigma\) de la muestra para calcular el error estándar:

\(SE[\overline{X}]=\frac{\sigma}{\sqrt{n}}\)

Donde \(\overline{X}\) es el promedio de nuestra muestra aleatoria y \(n\) es el tamaño de muestra.

7.7 Ejercicios

La data más común que gestiona un Data Scientist proviene de personas, algún atributo/característica de ellos. En estos ejercicios vamos a utilizar el data frame de alturas que y a utilizamos para otros propósitos en capítulos anteriores.

  1. Crea el vector x para extraer los datos de las alturas de cada persona. Luego reporta el promedio y la desviación estándar de nuestra población. Recuerda convertir la estatura a metros

Solución

Matemáticamente usamos x en minúscula para referirnos a nuestra población total y X para referirnos a una muestra aleatoria. La media de la población la denotaremos como \(\mu\) y la desviación estándar de la población como \(\sigma\)

La mayor cantidad de veces no tendremos acceso a la media y desviación estándar de la población porque es muy grande y es altamente costoso.

  1. Asumamos que no tenemos acceso a la población. Solo podemos obtener una muestra aleatoria de 100 personas. Crea una muestra aleatoria con reemplazo y almacena estos valores en el vector llamado X. Con los datos de tu muestra, construye un intervalo de confianza del 95% para estimar el promedio de la población.

Solución

  1. Utilizando simulación de Montecarlo, repite este muestreo unas 10 mil veces y valida el porcentaje de veces que el intervalo de confianza que generas a raíz de tu muestra incluye el verdadero valor de la población.

Solución