Capítulo 11 Aprendizaje No supervisado
Ahora que ya sabemos cómo crear algoritmos de aprendizaje supervisado, entender el no supervisado se convierte en un ejercicio intuitivo.
Mientras que en el aprendizaje supervisado tenemos un conjunto de variables que usamos para predecir una determinada clase de salida (sube/baja, renuncia/no renuncia), en el aprendizaje no supervisado no tenemos clases de salida esperadas. En el aprendizaje supervisado teníamos data de entrenamiento y data de testeo que nos permitía validar la efectividad del modelo por la cercanía a la clase conocida. En el aprendizaje no supervisado no tenemos output predeterminado. Esto genera a su vez un gran reto porque es muy difícil saber si ya culminamos con el trabajo o podemos aun generar otro modelo con el que nos sintamos más satisfechos.
El ejemplo más sencillo para entender este tipo de aprendizaje es cuando tenemos nuestra base de clientes y queremos segmentarlos por primera vez. En ese caso buscamos clientes que se comporten de la misma forma, pero al ser la primera vez no sabemos cuántos segmentos podemos tener. El reto está en determinar el corte de ¿cuántos segmentos buscamos crear?.
Las principales aplicaciones del aprendizaje no supervisado están relacionadas en el agrupamiento o clustering de datos. Aquí, el objetivo es encontrar subgrupos homogéneos dentro de los datos. Estos alogoritmos se basan en la distancia entre observaciones. El ejemplo de la segmentación de clientes sería un ejemplo de clustering.
Los algoritmos más utilizados de agrupamiento son: agrupamiento por k-medias y agrupamiento jerárquico.
11.1 Agrupamiento por k-medias
Para entender este método utilizaremos ejemplos primero con una cantidad mínima de variables y luego poco a poco iremos creando un modelo más genérico.
11.1.1 Agrupamiento con k = 2
Supongamos que tenemos un listado de jugadores en un campo de fútbol y tomamos una foto desde arriba para tener sus coordenadas (variable 1 sería el eje x y variable 2 sería el eje y). No podemos ver de qué equipo es cada jugador así que a todos los pintaremos como puntos negros.
jugadores <- tibble(x = c(-1, -2, 8, 7, -12, -15, -13, 15, 21, 12, -25, 26),
y = c(1, -3, 6, -8, 8, 0, -10, 16, 2, -15, 1, 0)
)
jugadores %>%
ggplot() +
aes(x, y) +
geom_point(size = 5)
Este método nos permite agrupar a partir de la definición de centroides. Definiremos tantos centroides como grupos queremos obtener. Como para este caso sabemos que deben de haber dos equipos utilizaremos 2 centroidoes (k = 2)
El algoritmo k-medias coloca entonces en una primera iteración estos 2 puntos (centroides) de forma aleatoria en el plano. Luego, calcula la distancia entre cada centro y los demás puntos de la data. Si está más cercano a un centroide entonces lo asigna al centroide 1, sino al centroide 2.
Ya se ha realizado una primera agrupación. Ahora cada centroide dentro de cada grupo se ubica en la media de los demás puntos de su grupo y se da otra iteración para volver a asignar a todos los puntos. Esta iteración se hace una y otra vez hasta que los centroides quedan fijos.
Para crear este modelo en R utilizaremos la función kmeans(data, centers = k).
modelo_kmeans <- kmeans(jugadores, centers = 2)
# Imprimimos las coordenadas de los centros
modelo_kmeans$centers
#> x y
#> 1 -11.33333 -0.5000000
#> 2 14.83333 0.1666667Esto quiere decir que para estos dos centros la distancia promedio a los otros puntos es la mínima, por ende el algoritmos los asigna a un grupo u otro. Veamos aproximadamente dónde se encuentran estos centros si los marcásemos con una equis.
Así, una vez creado el modelo podemos obtener los resultados del agrupamiento, equipo 1 o equipo 2.
Esta asignación de equipos los podemos agregar como una columna más de nuestro data set jugadores para poder visualizarlos en R.
# Agregamos la columna del cluster
jugadores_agrupados <- jugadores %>%
mutate(cluster = equipo)
# Visualizamos los jugadores de acuerdo a la agrupación
jugadores_agrupados %>%
ggplot() +
aes(x, y, fill = factor(cluster)) +
geom_point(size = 5, pch = 21) +
scale_fill_manual(values=c("#EE220D", "#01A2FF")) +
theme(legend.position = "none")
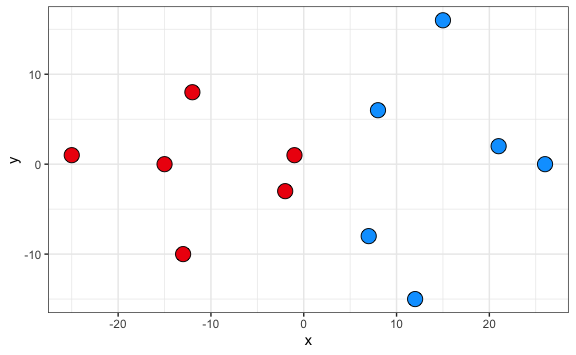
Hemos encontrado dos centroides hasta minimizar la suma de los cuadrados de diferencia entre cada centroide y los demás puntos del clúster. Podemos acceder y ver cuánto es este valor, dado que es parte de los resultados del modelo.
# Suma de cuadrados dentro de cada cluster
modelo_kmeans$withinss
#> [1] 570.8333 863.6667
# Total
modelo_kmeans$tot.withinss
#> [1] 1434.5Tot.withinss viene del inglés _Total within-cluster sum of squares` que significa suma total de cuadrados dentro del clúster.
11.1.2 Agrupamiento con k >= 3
Cuando tenemos 3 o más centros la idea es la misma, solo cambiamos el parámetro centers.
modelo_kmeans <- kmeans(jugadores, centers = 3)
equipo <- modelo_kmeans$cluster
jugadores_agrupados <- jugadores %>%
mutate(cluster = equipo)
jugadores_agrupados %>%
ggplot() +
aes(x, y, color = factor(cluster)) +
geom_point(size = 5) +
theme(legend.position = "none")
modelo_kmeans$tot.withinss
#> [1] 1071.25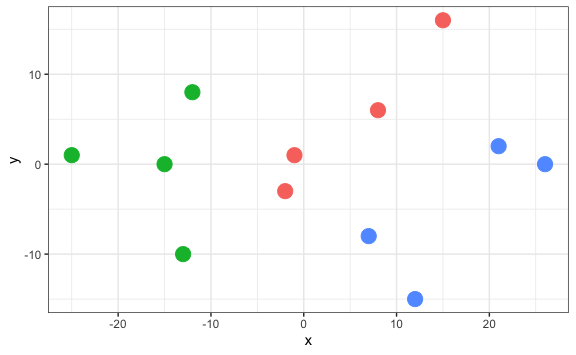
En este caso hemos encontrado que la suma de cuadrados dentro de los clusters es menor, con lo que podríamos indicar que este agrupamiento es más óptimo que el agrupamiento en dos grupos. Sin embargo, la suma de cuadrados no necesariamente es el mejor indicador para elegir cuántos clusters crear.
11.1.3 Determinación de clústeres óptimos
Podemos utilizar principalmente dos métodos para determinar cuántos clusters deberíamos de construir, k. El método de suma de cuadrados (wss por las siglas en inglés de Within Sum Square) y el método de silueta promedio (silhouette en inglés)
Para no tener que calcular modelos para diferentes valores de k utilizaremos la libería factoextra, la cual fue creada especialmente para realizar análisis de datos multivariados fáciles y de visualización elegante, muy útil para agrupación.
11.1.3.1 Método de suma de cuadrados
Para encontrar el “k” óptimo bajo éste método usaremos el diagrama del codo, donde primero calculamos el total de la suma total de cuadrados dentro del clúster para diferentes valores de “k”. Luego, visualmente identificaremos un punto donde haya habido una caída muy fuerte seguida de una caída más gradual de la pendiente. Para ello usaremos la función fviz_nbclust(data, tipo, metodo) e ingresaremos nuestra data, el tipo de algoritmo que se usará para agrupar y el método de medición.
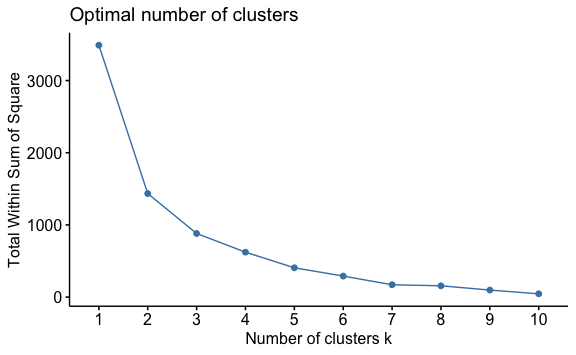
En este caso el “codo” se encuentra en el valor k = 2, a partir de ahí el suma de cuadrados se reduce pero a un ritmo más lento.
11.1.3.2 Método de silueta promedio
El método descrito anteriormente es una ayuda visual que hace difícil el reconocimiento cuando los datos son más cercanos. Por ello, es mucho más frecuente realizar un análisis de siluetas (Rousseeuw 1987). Este enfoque mide la calidad de una agrupación. Es decir, se determina qué tan bien se encuentra cada objeto dentro de su grupo. Un alto ancho de silueta promedio indica un buen agrupamiento. El método de la silueta promedio calcula la silueta promedio de las observaciones para diferentes valores de “k”. El número óptimo de grupos “k” es el que maximiza la silueta promedio en un rango de valores posibles para “k”.
Para ello, cambiamos el parámetro method en la función y obtenemos el análisis de silueta.
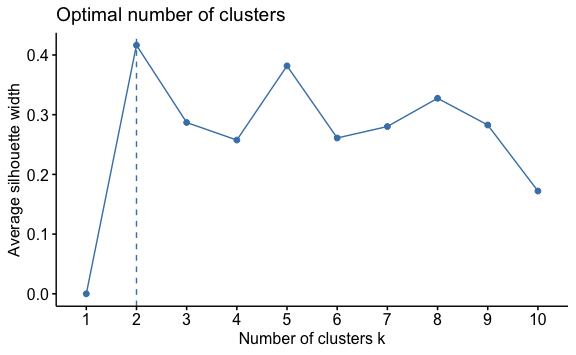
Aquí se ve claramente que para un valor de k=2 tenemos el mejor promedio, con lo que éste se convierte en nuestro número de grupos óptimo.
11.1.4 k-medias para más de 2 variables
El método que hemos aprnedido se puede extender fácilmente a más variables. Solo que en este caso ya no sería posible visualizarlo como el equipo de fútbol y visualizaríamos solo los resultados de la agrupación y las métricas aprendidas.
Para ello, utilizaremos el siguiente dataset de clientes, en el que encontraremos un conjunto de datos de clientes de un distribuidor mayorista. Incluye el gasto anual en unidades monetarias en diversas categorías de productos.
url <- "http://archive.ics.uci.edu/ml/machine-learning-databases/00292/Wholesale%20customers%20data.csv"
clientes <- read_csv(url)
#> Parsed with column specification:
#> cols(
#> Channel = col_double(),
#> Region = col_double(),
#> Fresh = col_double(),
#> Milk = col_double(),
#> Grocery = col_double(),
#> Frozen = col_double(),
#> Detergents_Paper = col_double(),
#> Delicassen = col_double()
#> )Vamos a realizar una agrupación solo considerando el gasto realizado en comidas congeladas, abarrotes y lácteos.
Una vez tenemos nuestra data crearíamos un análisis de siluestas para determinar el mejor valor de “k”.
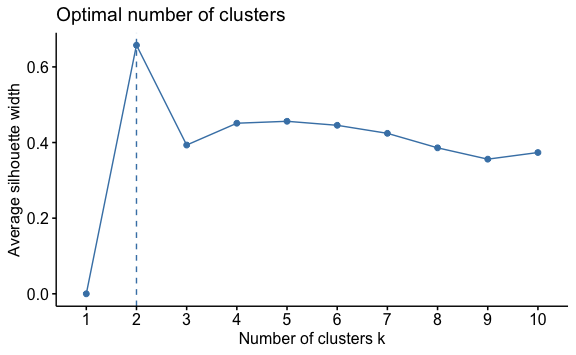
Nuevamente obtenemos que la cantidad de clusters recomendados es 2. Creemos entonces el modelo para k = 2 y almacenemos el clúster resultante.
modelo <- kmeans(clientes_filtrado, centers = 2)
clientes_agrupados <- clientes_filtrado %>%
mutate(cluster = modelo$cluster)
clientes_agrupados
#> # A tibble: 440 x 4
#> Milk Grocery Frozen cluster
#> <dbl> <dbl> <dbl> <int>
#> 1 9656 7561 214 1
#> 2 9810 9568 1762 1
#> 3 8808 7684 2405 1
#> 4 1196 4221 6404 1
#> 5 5410 7198 3915 1
#> 6 8259 5126 666 1
#> 7 3199 6975 480 1
#> 8 4956 9426 1669 1
#> 9 3648 6192 425 1
#> 10 11093 18881 1159 2
#> # … with 430 more rowsUna vez que tenemos agrupados nuestros datos podemos calcular la cantidad de datos en cada cluster y la media de los valores para cada grupo y así identificar diferencias entre estos dos potenciales segmentos de clientes.
clientes_agrupados %>%
group_by(cluster) %>%
summarise(total = n(),
media_Milk = mean(Milk),
media_Grocery = mean(Grocery),
media_Frozen = mean(Frozen))
#> # A tibble: 2 x 5
#> cluster total media_Milk media_Grocery media_Frozen
#> <int> <int> <dbl> <dbl> <dbl>
#> 1 1 388 3955. 5386. 2902.
#> 2 2 52 19534. 27094. 4341.Así, hemos aprendido a segmentar clientes utilizando machine learning.
11.2 Agrupamiento jerárquico
El agrupamiento jerárquico es otro método para agrupar datos. La palabra jerárquico viene a raíz de las jerarquías que este algoritmo crea para determinar los clusters. A diferencia del k-medias no partimos indicando cuántos clusters queremos crear, sino que el algoritmo nos muestra un listado de combinaciones posibles de acuedo a la jerarquía de las distancias entre puntos. Veámoslo con un ejemplo.
11.2.1 Agrupamiento con dos variables
Para ello utilizaremos el mismo ejemplo del equipo de fútbol que utilizamos anteriormente. Con la diferencia que esta vez numeramos cada jugador para hacer más fácil la visualización.
nro <- 1:12
jugadores <- tibble(x = c(-1, -2, 8, 7, -12, -15, -13, 15, 21, 12, -25, 26),
y = c(1, -3, 6, -8, 8, 0, -10, 16, 2, -15, 1, 0))
jugadores %>%
ggplot() +
aes(x, y, label = nro) +
geom_point(size = 5) +
geom_text(nudge_x = 1.3, nudge_y = 1.3)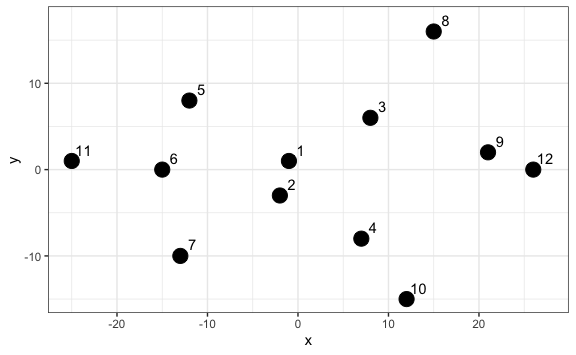
Este algoritmo busca los dos puntos con la distancia más corta, los más cercanos, y los agrupa. Luego busca otros dos puntos con la menor distancia y pregunta: ¿la distancia entre estos dos nuevos puntos es menor que la distancia de estos puntos al grupo creado antes? Si la respuesta es sí los agrupa, sino agrupa el punto más cercano al primer grupo creado.
Entendamos el algoritmo gráficamente. Los puntos 1 y 2 tienen la jerarquía más baja dado que tienen la distancia más corta. Luego el algoritmo busca por los siguientes dos puntos más cercanos (el punto 9 y el 12) y al comparar con el punto medio del 1 y 2 opta por crear un nuevo grupo con una jerarquía ligeramente más alta y así sucesivamente.
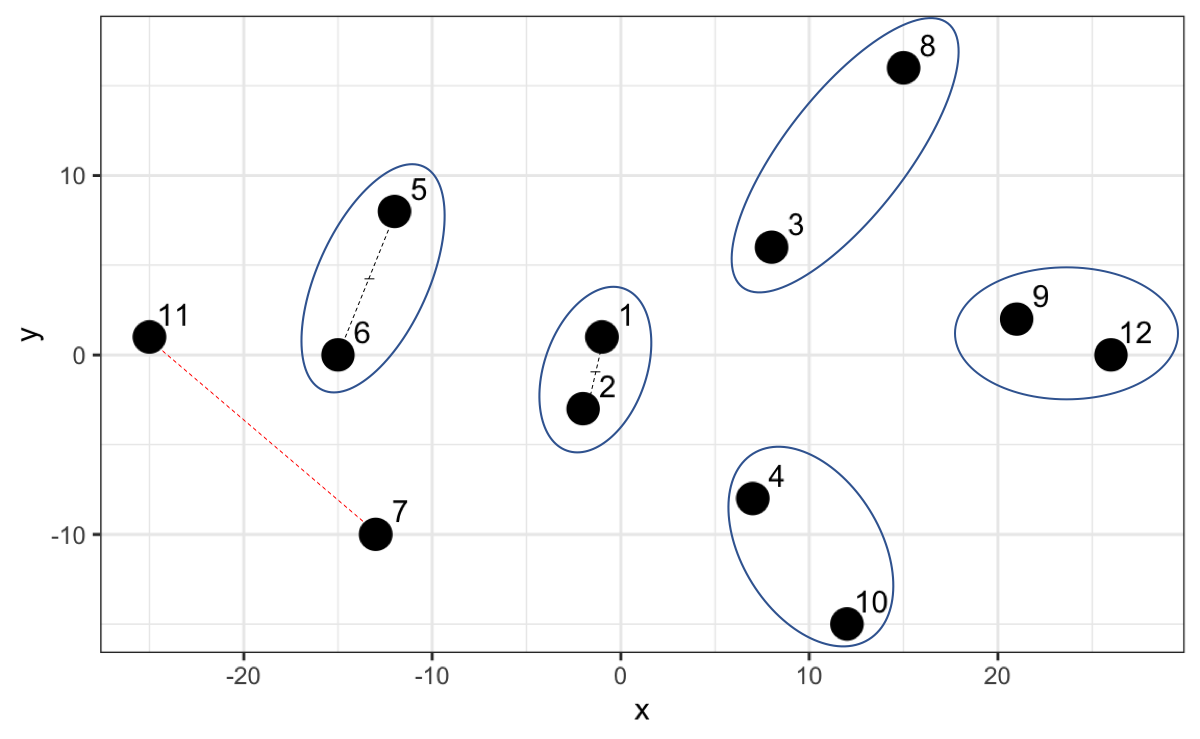
Sin embargo, ahora que tenemos el punto 7 y 11 y calculamos la distancia resulta que esa distancia no es la menor comparado a las distancias con los otros grupos existentes Por ejemplo, el 7 está más cerca al punto medio del 1 y 2, y el 11 está más cerca al punto medio del 5 y 6.
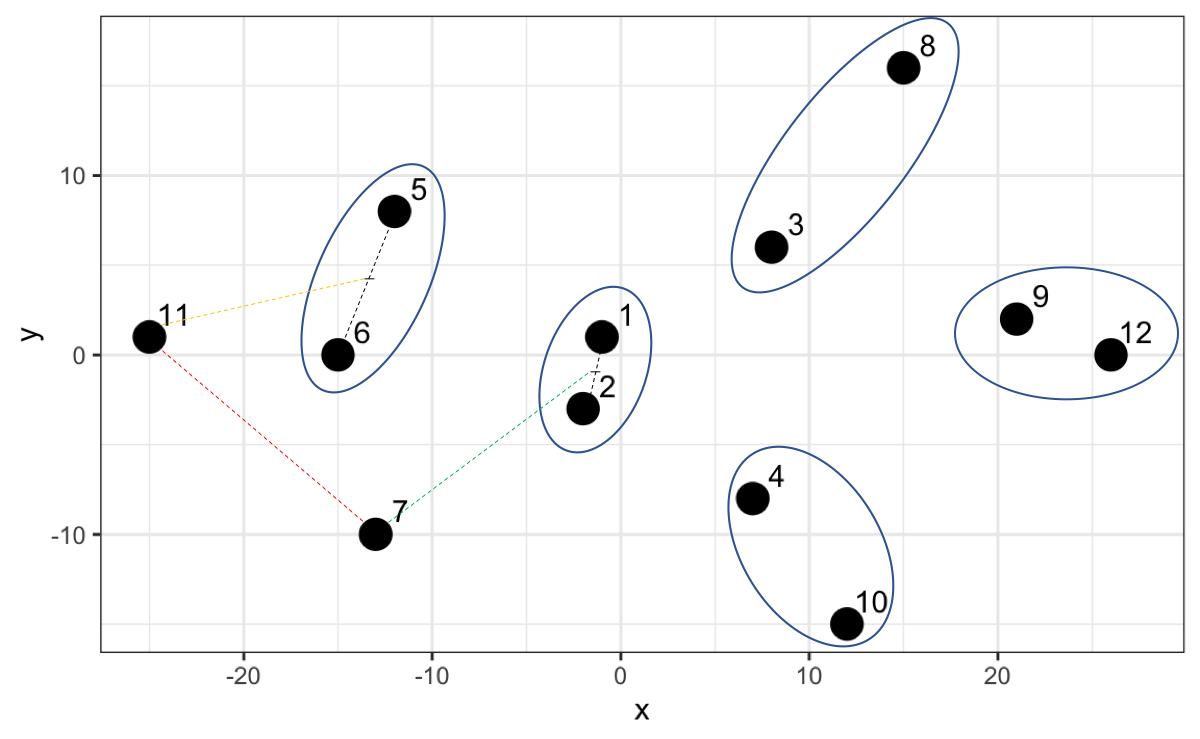
Así, el algoritmo crea una jerarquía más alta para esta agrupación.
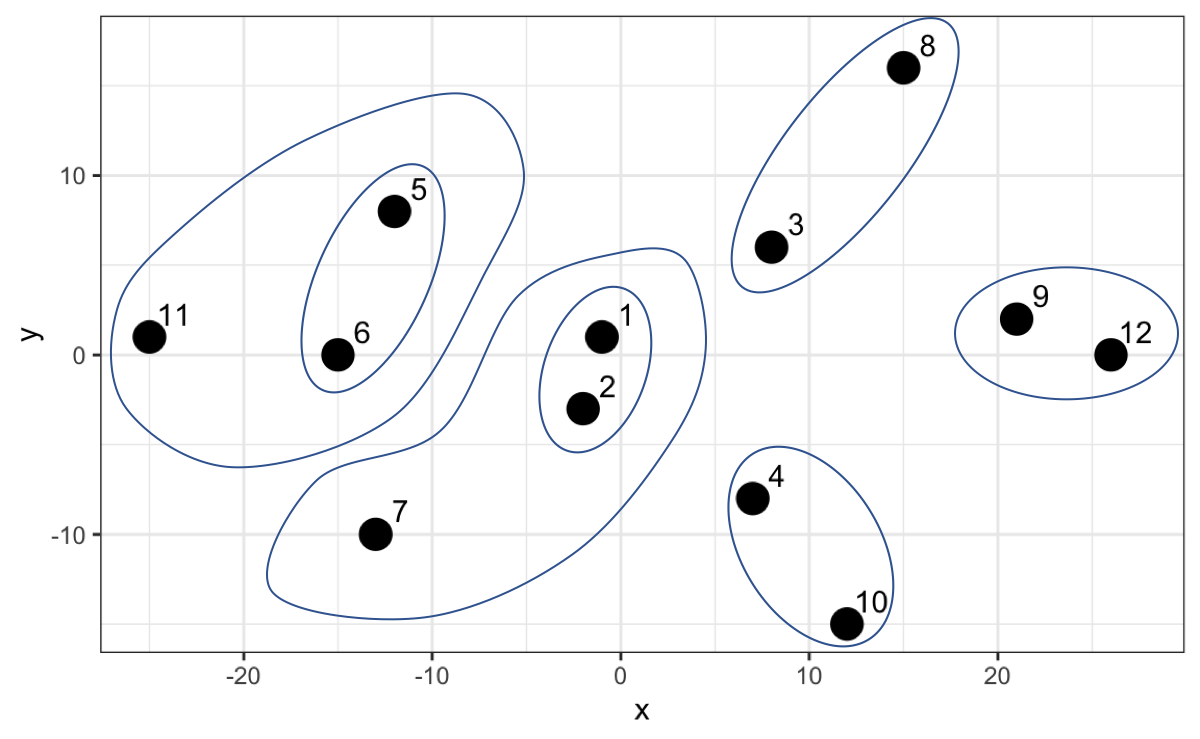
El algoritmo continua hasta que finalmente crea un grupo que contempla a todos como la jerarquía más alta. En el siguiente gráfico no solo podemos apreciar ello sino también en el eje y la distancia entre cada punto o grupo de puntos.
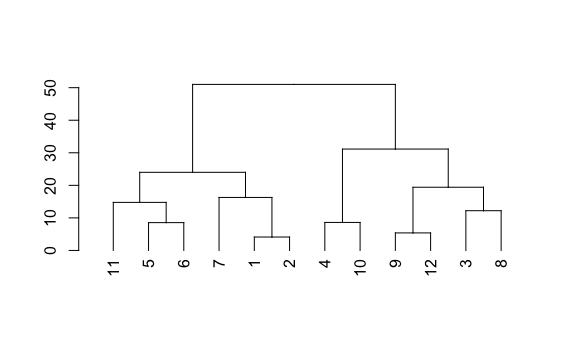
Hasta acá aun no hemos más que generado jerarquías a partir de las distancias que nos servirá luego para determinar cuántos cluster generar. Creemos en R lo avanzado hasta ahora. Lo primero que haremos es calcular las distancias entre todos los puntos. Para ello usaremos la función dist().
Con las distancias calculadas podemos crear el modelo jerárquico utilizando la función hclust(matriz_distancias)
Una vez creado nuestro modelo podemos visualizarlo utilizando la librería dendextend.
La visualización que vimos se llama dendograma. Para ello solo tenemos que convertir nuestro modelo a formato dendograma.
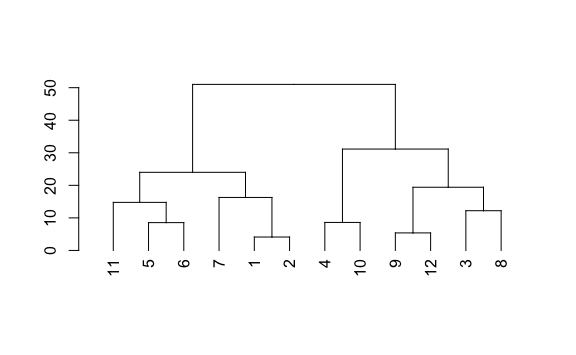
Hasta ahora solo hemos la jerarquía, pero lo que nos interesa es la agrupación. La agrupación se realiza por la distancia calculada (parámetro h). Probemos con una distancia de 60. Usaremos las funciones color_branches y color_labels para hacer visible los cambios.
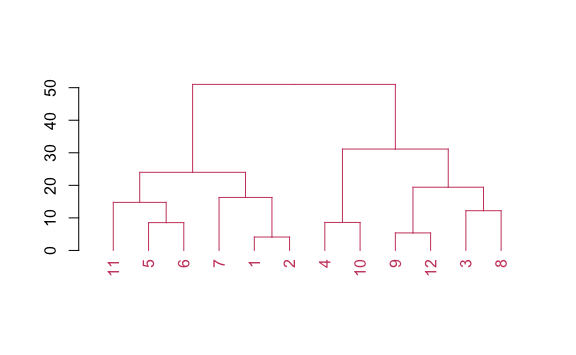
Como la distancia de jerarquía más alta es aproximadamente 50, entonces en este caso nos agrupa a todos en un gran clúster. Probemos con un número más bajo, por ejemplo 40.
corte <- 40
dend_modelo %>%
color_branches(h = corte) %>%
color_labels(h = corte) %>%
plot() %>%
abline(h = corte, lty = 2)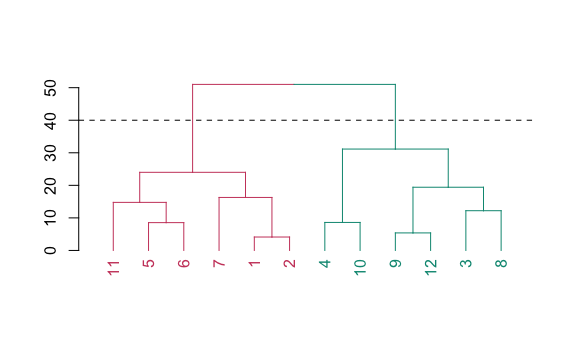
Al hacer un corte en 40 ahora tenemos dos cluster, en este caso el color rojo y el color verde. Probemos con un número más bajo, 28.
corte <- 28
dend_modelo %>%
color_branches(h = corte) %>%
color_labels(h = corte) %>%
plot() %>%
abline(h = corte, lty = 2)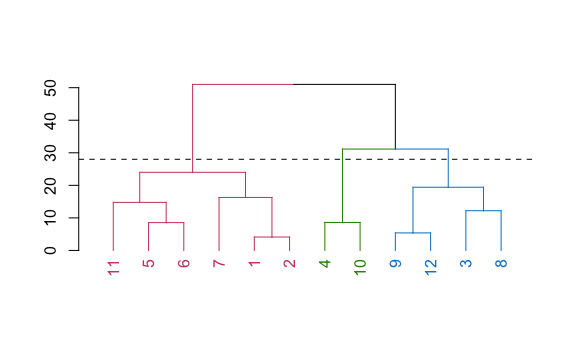
Ahora tenemos tres clúster y así podríamos ir continuando hasta obtener los clústers que necesitamos.
Habremos notado lo impráctico que es utilizar las distancias del modelo jerárquico porque éstas varían de acuerdo a los datos que tengamos. Este modelo nos permite hacer cortes no solo por distancias sino también indicando cuántos clúster queremos, parámetro k.
clusters_deseados <- 3
dend_modelo %>%
color_branches(k = clusters_deseados) %>%
color_labels(k = clusters_deseados) %>%
plot()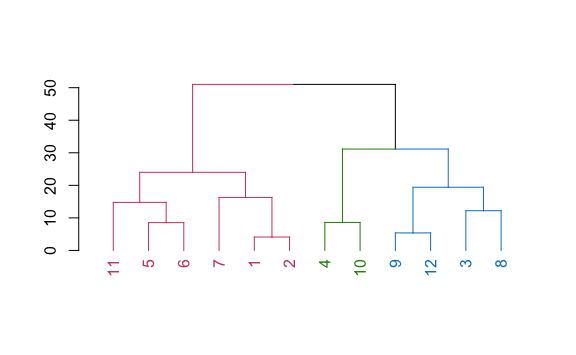
Vemos que nos da la misma agrupación si utilizamos distancias o número de clusters deseados.
11.2.2 Determinación de clústeres óptimos
Para calcular cuántos clústeres son óptimos crear utilizaremos nuevamente el análisis de silueta, pero esta vez con el argumento FUN = hcut para determinar que se evalúe en base a un modelo jerárquico.
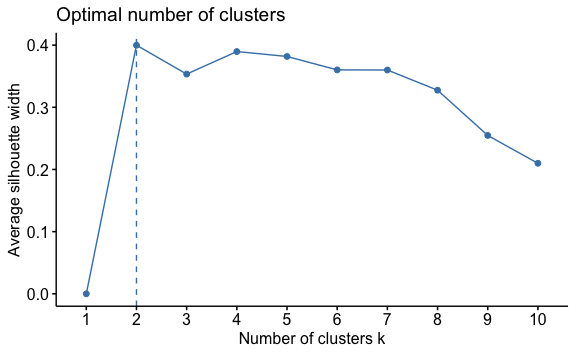
No es de sorprender que el valor de k también es 2, el cual coincide con el número obtenido en el modelo k-medias.
11.2.3 Obtener la agrupación
Ahora que hemos validado que el número de clusters recomendado es 2 calculamos la agrupación a partir del modelo antes creado.
jugadores_agrupados <- jugadores %>%
mutate(cluster = cutree(modelo_jerarquico, k = 2)
)
jugadores_agrupados
#> # A tibble: 12 x 3
#> x y cluster
#> <dbl> <dbl> <int>
#> 1 -1 1 1
#> 2 -2 -3 1
#> 3 8 6 2
#> 4 7 -8 2
#> 5 -12 8 1
#> 6 -15 0 1
#> 7 -13 -10 1
#> 8 15 16 2
#> 9 21 2 2
#> 10 12 -15 2
#> 11 -25 1 1
#> 12 26 0 2Finalmente, visualicemos la agrupación realizada con este método.
jugadores_agrupados %>%
ggplot() +
aes(x, y, color = factor(cluster)) +
geom_point(size = 5) +
theme(legend.position = "none")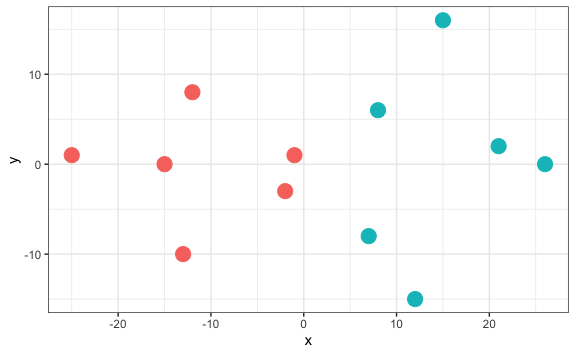
Vemos que la agrupación es la misma que con el anterior método, básicamente porque estamos hablando de dos variables y dos clusters.
Ambos métodos aprendidos son muy flexibles, con lo que la creación de modelos para más variables sigue la misma lógica aprendida en estas secciones.
11.3 Reducción de dimensionalidad
Hemos creado clusters con un número de variables controlado. Sin embargo, vamos a encontrarnos en muchos casos con muchas más variables que hacen difícil la interpretación y es importante identificar si dos variables tienen el mismo comportamiento para poder tomar solo una de ellas.
Para este caso vamos a tomar de ejemplo un datasets de clientes de tarjeta de crédito, adaptación del dataset público en Kaggle, de la siguiente ruta.
url <- "https://dparedesi.github.io/DS-con-R/tarjetas_de_credito.csv"
tarjetas <- read_csv(url)
#> Parsed with column specification:
#> cols(
#> balance = col_double(),
#> frecuencia_balance = col_double(),
#> compras = col_double(),
#> compras_primeros_tres_meses = col_double(),
#> primera_compra = col_double(),
#> adelanto_efectivo = col_double(),
#> frecuencia_compras = col_double(),
#> frecuencia_adelanto_efectivo = col_double(),
#> compras_transacciones = col_double(),
#> linea_credito = col_double(),
#> pagos = col_double(),
#> pago_minimo = col_double(),
#> permanencia = col_double()
#> )Tenemos más de 8 mil clientes con 13 atributos. Analizaremos si hay variables fuertemente correlacionadas. Para ello utilizaremos la librería corrplot.
A continuación, ingresaremos el dataset para visualizar correlaciones entre las variables,
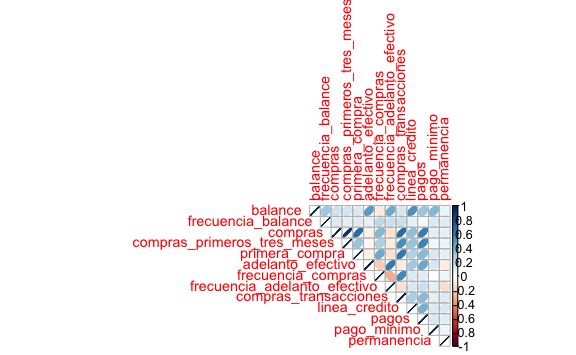
Hay una fuerte correlación entres la variable total de compras y las compras realizadas en los 3 primeros meses. Podemos visualizarl estas dos variables para validar.
tarjetas %>%
ggplot() +
aes(x=compras, y=compras_primeros_tres_meses) +
geom_point() +
labs(title="Atributos de clientes",
subtitle="Relación entre total de compras y 3 primeros meses")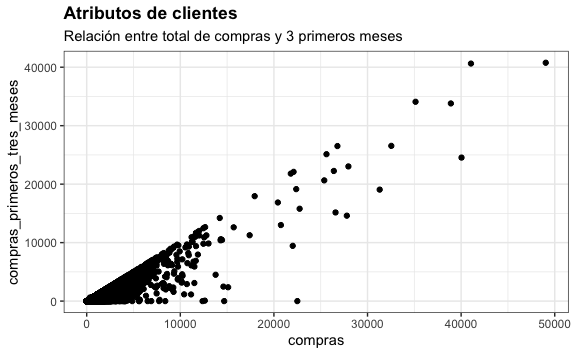
Dado ello, podríamos incluir dentro de nuestro análisis solo una de estas dos variables.
También podríamos validar la distribución de estas variables.
# Removemos variable compras 3 primeros meses
tarjetas <- tarjetas[, !names(tarjetas) == "compras_primeros_tres_meses"]
tarjetas %>%
gather(atributos, valores) %>%
ggplot() +
aes(x=valores, fill=atributos) +
geom_histogram(colour="black", show.legend=FALSE) +
facet_wrap(~atributos, scales="free_x") +
labs(x="Valores", y="Frecuencia",
title="Atributos de clientes - Histograma")
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.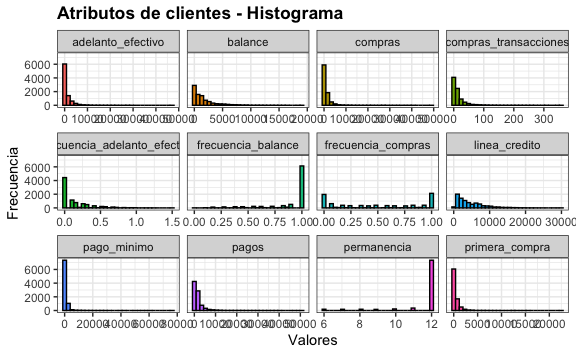
Vemos concentraciones de datos en algunas variables como permanencia (tiempo que lleva nuestro cliente con nosotros). Podemos validarlo haciendo un zoom a esa variable.
boxplot(tarjetas$permanencia)
prop.table(table(tarjetas$permanencia))
#>
#> 6 7 8 9 10 11 12
#> 0.02130616 0.02049560 0.02119037 0.01899027 0.02616952 0.04122279 0.85062529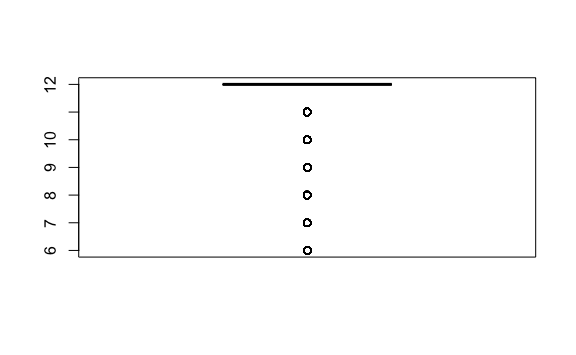
El 85% de nuestros datos son de clientes que llevan con nosotros 12 meses. Podríamos optar por filtar los datos para hacer un análisis sobre los clientes que tienen 1 año y así retirar esta variable del agrupamiento.
tarjetas <- tarjetas %>%
filter(permanencia == 12)
tarjetas <- tarjetas[, !names(tarjetas) == "permanencia"]
#Lo mismo haremos con la variable frecuencia_balance
prop.table(table(tarjetas$frecuencia_balance))
#>
#> 0 0.090909 0.181818 0.272727 0.363636 0.454545
#> 0.000816771 0.003403213 0.015518650 0.018241220 0.021508304 0.022325075
#> 0.545455 0.636364 0.727273 0.818182 0.909091 1
#> 0.027634087 0.026545059 0.028178601 0.034712769 0.041927580 0.759188674
tarjetas <- tarjetas %>%
filter(frecuencia_balance == 1)
tarjetas <- tarjetas[, !names(tarjetas) == "frecuencia_balance"]Si además analizamos las distribuciones de cada variable encontramos lo siguiente:
summary(tarjetas)
#> balance compras primera_compra adelanto_efectivo
#> Min. : 1.592 Min. : 0.00 Min. : 0.0 Min. : 0.0
#> 1st Qu.: 471.105 1st Qu.: 46.65 1st Qu.: 0.0 1st Qu.: 0.0
#> Median : 1304.460 Median : 478.32 Median : 136.0 Median : 58.7
#> Mean : 2066.117 Mean : 1236.09 Mean : 499.6 Mean : 1028.0
#> 3rd Qu.: 2748.609 3rd Qu.: 1455.68 3rd Qu.: 600.0 3rd Qu.: 1191.5
#> Max. :19043.139 Max. :49039.57 Max. :15497.2 Max. :47137.2
#> frecuencia_compras frecuencia_adelanto_efectivo compras_transacciones
#> Min. :0.00000 Min. :0.00000 Min. : 0
#> 1st Qu.:0.08333 1st Qu.:0.00000 1st Qu.: 1
#> Median :0.58333 Median :0.08333 Median : 11
#> Mean :0.54879 Mean :0.14872 Mean : 19
#> 3rd Qu.:1.00000 3rd Qu.:0.25000 3rd Qu.: 24
#> Max. :1.00000 Max. :1.00000 Max. :358
#> linea_credito pagos pago_minimo
#> Min. : 150 Min. : 14.5 Min. : 3.2
#> 1st Qu.: 1800 1st Qu.: 529.8 1st Qu.: 209.9
#> Median : 4000 Median : 1074.3 Median : 477.5
#> Mean : 4884 Mean : 1934.7 Mean : 1113.3
#> 3rd Qu.: 7000 3rd Qu.: 2125.9 3rd Qu.: 1090.5
#> Max. :25000 Max. :46930.6 Max. :76406.2Vemos que hay variables que tienen máximos de 1, como hay otras que tienen un máximo de 30 mil o 50 mil. Ya habíamos visto anteriormente la importancia de normalizar los datos. Acá también lo haremos con la función scale().
Podemos comprobar que la distribución no cambia, solo la escala.
tarjetas_norm %>%
gather(atributos, valores) %>%
ggplot() +
aes(x=valores, fill=atributos) +
geom_histogram(colour="black", show.legend=FALSE) +
facet_wrap(~atributos, scales="free_x") +
labs(x="Valores", y="Frecuencia",
title="Atributos de clientes - Histograma")
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.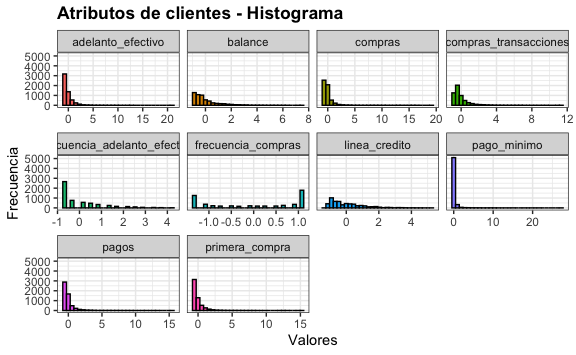
La preparación de datos y reducción de variables es un paso necesario cuando creamos modelos de machine learning. Sin embargo debemos de realizarlo con cuidado, dado que en este ejercicio al preparar los datos si bien tenemos menos variables (10), también tenemos menos filas.
str(tarjetas_norm)
#> 'data.frame': 5577 obs. of 10 variables:
#> $ balance : num 0.188 -0.547 -0.112 -0.63 -0.106 ...
#> $ compras : num -0.1871 -0.4932 0.0393 2.3667 -0.3233 ...
#> $ primera_compra : num -0.5081 -0.5081 0.8478 0.192 -0.0645 ...
#> $ adelanto_efectivo : num -0.473 -0.473 -0.473 -0.473 -0.473 ...
#> $ frecuencia_compras : num 1.085 -1.119 0.283 1.085 1.085 ...
#> $ frecuencia_adelanto_efectivo: num -0.728 -0.728 -0.728 -0.728 -0.728 ...
#> $ compras_transacciones : num -0.238 -0.612 -0.374 1.529 -0.238 ...
#> $ linea_credito : num 0.695 -0.979 -0.82 2.29 -0.687 ...
#> $ pagos : num -0.448 -0.428 -0.182 1.507 -0.428 ...
#> $ pago_minimo : num -0.173 -0.31 0.462 -0.327 -0.207 ...Técnicas más avanzadas como el análisis de componentes principales (PCA) y el valor singular de descomposición (SVD) son utilizadas para realizar la reducción de dimensionalidad de forma más rigurosa para no perder tantos datos en nuestro análisis. Sin embargo, su interpretación aun está en desarrollo por la alta complejidad matemática que requiere para su entendimiento.
11.4 Ejercicios
En los siguientes ejercicios trabajaremos sobre data de posts de 10 empresas de fashion que tienen sus páginas en Facebook y las reacciones de sus seguidores. Para ello, trabajaremos con la data en el siguiente repositorio:
url <- "http://archive.ics.uci.edu/ml/machine-learning-databases/00488/Live.csv"
posts <- read_csv(url)
# Eliminamos columnas no relevantes para el análisis
columnas_no_relevantes <- c("status_type","status_id", "status_published", "Column1",
"Column2", "Column3", "Column4")
data_posts <- posts[, !names(posts) %in% columnas_no_relevantes]- Con el objeto
data_postsnormalizado (usar funciónscale()) y crea el objetodata_posts_norm. Construye un gráfico de siluetas para determinar cuántos grupos cluster son recomendados usando el algoritmo k-medias.
Solución
- Con el objeto
data_postsconstruye un gráfico de siluetas para determinar cuántos grupos cluster son recomendados usando el algoritmo jerárquico.
- Si tuvieras que eliminar una variable del análisis, ¿qué variable sería?
Solución
- Elimina la variable
num_reactionsdel objetodata_posts_normy del objetodata_postsy vuelve a realizar un análisis de siluetas usandodata_posts_norm. ¿Cambia el número de clústers?
Solución
- Crea el modelo de k-medias para agrupar utilizando el número de clústers recomendado encontrado. Utilizar el objeto
data_posts_normpara la creación del modelo. Crear el objetodata_posts_agrupadosdonde esté la data original dedata_postscon la columna adicionalcluster_mediasindicando el cluster resultado de este modelo.
Solución
- Crea el modelo jerárquico para agrupar utilizando el número de clústers recomendado encontrado. Utilizar el objeto
data_posts_normpara la creación del modelo. Agregar al objetodata_posts_agrupadosla columnacluster_jerpara almacenar el resultado del agrupamiento.
Solución
- Calcula el promedio de cada valor de las variables por cada grupo del modelo k-medias.
Solución
- Calcula el promedio de cada valor de las variables por cada grupo del modelo jerárquico.
Referencias
Rousseeuw, Peter J. 1987. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. Science Diret. https://www.sciencedirect.com/science/article/pii/0377042787901257/pdf?pid=1-s2.0-0377042787901257-main.pdf.