Capítulo 12 Aprendizaje Supervisado

Para entender el aprendizaje supervisado de forma intuitiva usaremos un ejemplo cotidiano. Todos hemos ido al doctor y alguna vez le hemos dicho que nos duele la garganta, que hemos tenido dolor de cabeza y fiebre. Éste nos hará unas cuantas preguntas más y luego nos dirá qué enfermedad podríamos tener y qué tratamiento seguir.

Intuitivamente sabemos que el doctor tuvo que entrenar inicialmente a partir de clases y libros donde muestran casos pasados, y estudiar qué síntomas son señal de cada enfermedad. Luego, empezó a testear lo aprendido en un grupo de pacientes durante su internado. Finalmente, cuando ya estaba entrenado tuvo licencia para poder aplicar este aprendizaje a pacientes en su consultorio u hospital.

Este es un ejemplo de aprendizaje supervisado porque el entrenamiento se realizó a partir de datos conocidos o inputs los cuales están etiquetados (duele la garganta, dolor de cabeza, fiebre) con la finalidad de obtener un resultado o output que también era conocido y etiquetado (¿tiene gripe o no?). Cuando un doctor testea lo aprendido se sabe los inputs de pacientes y también el output que es dado por un doctor con más experiencia que puede decir qué tan efectivo es su entrenamiento. Cuando el doctor sale a atender pacientes solo tendrá inputs etiquetados con la finalidad de predecir un output etiquetado.

Ésta es la lógica que se ha llevado a algoritmos computacionales. Lo podemos ver en facebook, quienes recopilan una serie de inputs, como nuestros likes, compartidos, etc, para predecir qué podríamos querer consumir y nos lo muestra a modo de recomendación. Y también lo veremos en nuestro ambiente de trabajo cuando tengamos inputs de nuestros clientes, como consumo, nivel adquisitivo, lugar donde vive, etc, para predecir cuál de nuestros productos predecimos que es más propenso a comprar y así llamarlo para ofrecerle ese producto.

12.1 Clasificacion y Regresión

Existen múltiples algoritmos de aprendizaje supervisado, pero los diferenciaremos en dos de acuerdo al tipo de variable que manejemos.

Cuando la variable sea discreta los llamaremos clasificación. Los ejemplos líneas arriba son muestra de ello. Hemos clasificado en dos clases (gripe o no) o varias clases (producto “x” a recomendar)

Cuando la variable sea continua los llamaremos regresión. La predicción de los precios de una casa dadas las características de la casa como tamaño, precio, etc. es uno de los ejemplos comunes de regresión.

En las siguientes secciones aprenderemos algunos algoritmos señalando si son de clasificación de regresión.

12.2 kNN: k vecinos más próximos

Comencemos por un simple, pero muy útil algoritmo de clasificación, el algoritmo de los k vecinos más próximos (kNN por sus siglas en inglés).

12.2.1 Dos variables como input

Comencemos por entenderlo visualmente. Imaginemos que tenemos dos variable como input y como output nos da si es Clase Roja o Clase Azul. Esta data es nuestra data de entrenamiento.

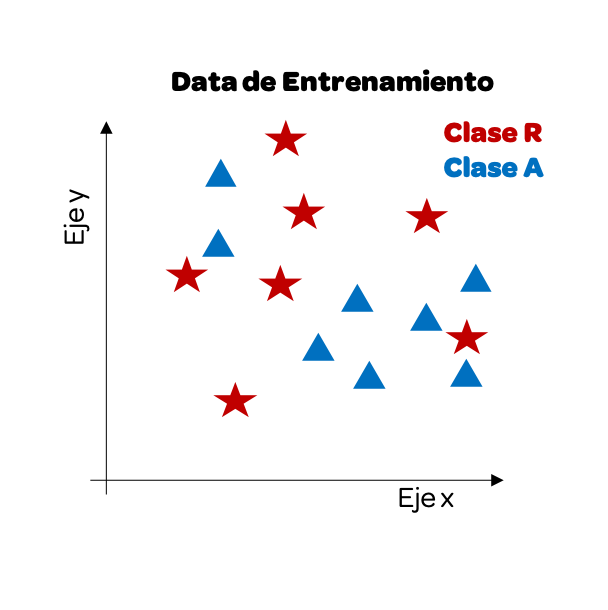
Ahora que ya tenemos nuestra data de entrenamiento empezaremos a usar la data de test. Como queremos predecir la clase, el output, veremos cómo uno de estos datos se vería visualmente y lo pintaremos de color amarillo. A continuación calculamos la distancia entre este punto y los demás datos.

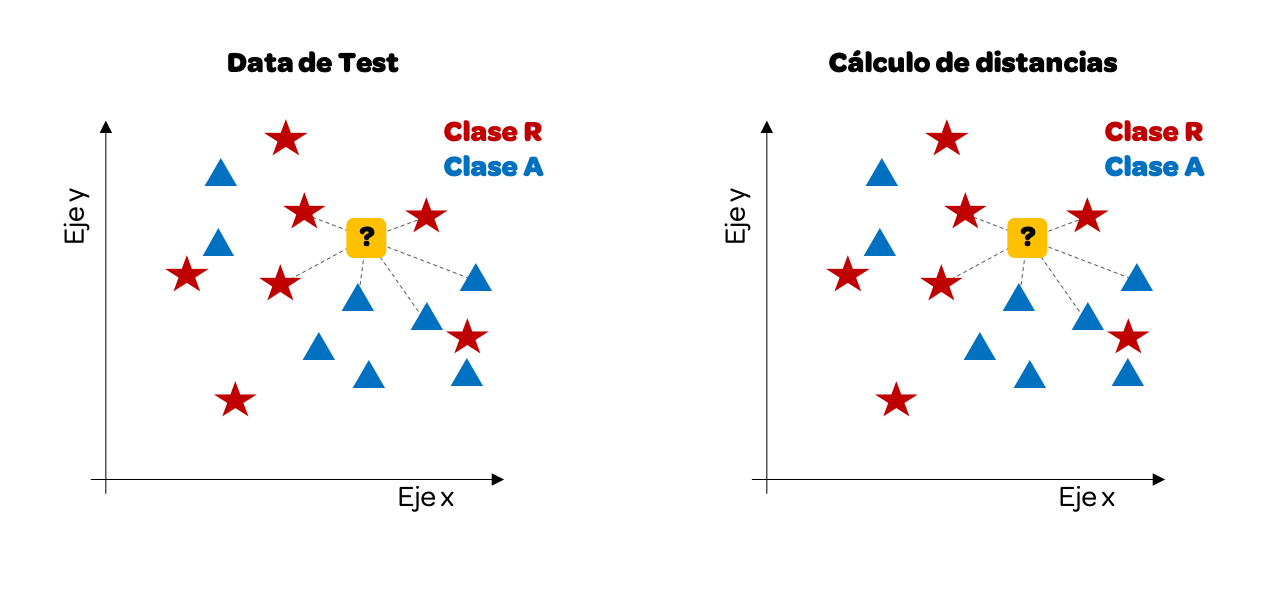
Hemos trazado solo algunas distancias, pero podríamos hacerlo con todos. Para este ejemplo tomaremos los k = 3 vecinos más cercanos.

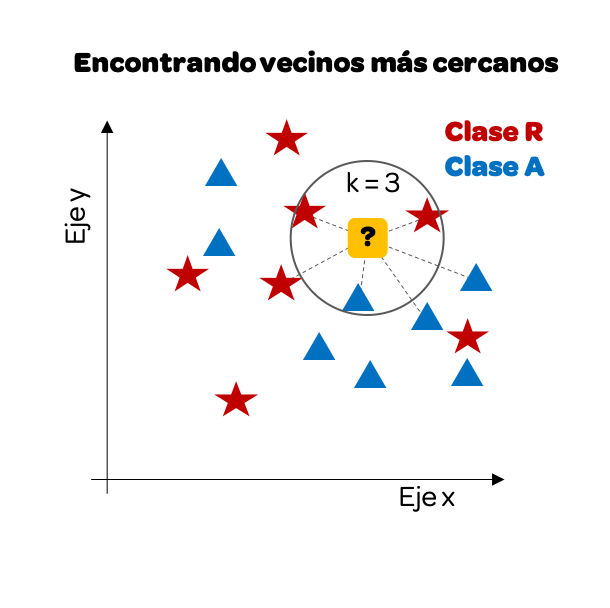
Notamos que si nos enfocamos solo en los 3 vecinos más cercanos hay más rojos que azules, entonces nuestra predicción será que este punto ha de ser clase R (rojo).

Calcular la distancia en un plano cartesiano es relativamente sencillo, solo tenemos variables como input: en el eje x y eje y. Sin embargo, la misma lógica se puede llevar a más variables.

12.2.2 Múltiples variables como input

Veamos cómo sería con 4 variables como input. Vamos a trabajar nuevamente con el data frame iris, el cual, como recordaremos, tiene 4 atributos de una planta y la última columna es la especie a la que pertenece.

data(iris)

iris %>% 
  head(10)
#>    Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#> 1           5.1         3.5          1.4         0.2  setosa
#> 2           4.9         3.0          1.4         0.2  setosa
#> 3           4.7         3.2          1.3         0.2  setosa
#> 4           4.6         3.1          1.5         0.2  setosa
#> 5           5.0         3.6          1.4         0.2  setosa
#> 6           5.4         3.9          1.7         0.4  setosa
#> 7           4.6         3.4          1.4         0.3  setosa
#> 8           5.0         3.4          1.5         0.2  setosa
#> 9           4.4         2.9          1.4         0.2  setosa
#> 10          4.9         3.1          1.5         0.1  setosa

La idea es la siguiente, tomaremos una data de entrenamiento, 50 datos. De esta data tenemos los 4 atributos de input y la última columna es el output, la especie. Utilizaremos el algoritmo kNN tomando como input esta data de entrenamiento para crear nuestro modelo. Luego, con una data de testing, otros 50 datos, probaremos nuestro modelo.

Comencemos tomemos una muestra aleatoria de 100 registros y separaremos la mitad para entrenamiento y la mitad para testear. Dado que tenemos 150 datos en nuestro data frame, tomemos una muestra de los índices. En este caso vamos a utilizar la función set.seed(n) para forzar a que los valores de la muestra aleatoria sean los mismos siempre. Así, poder todos obtener los mismos resultados y la explicación del libro en estos capítulos sea coherente con los resultados que cada lector obtenga. Para un ejercicio real no deberíamos de incluir esa línea. Se recomienda leer la documentación ?set.seed().

# 28 es el día de cumpleaños del autor
set.seed(28)

index_muestra <- sample(150, 100)

index_entrena <- sample(index_muestra, 50)

index_test <- index_muestra[!index_muestra %in% index_entrena]

Ahora que tenemos los índices podemos construir nuestra data de entrenamiento y nuestro test.

iris_entrena <- iris[index_entrena, ]
iris_test <- iris[index_test, ]

iris_entrena_input <- iris_entrena[, -5]
iris_entrena_output <- iris_entrena[, 5]

iris_test_input <- iris_test[, -5]
iris_test_output <- iris_test[, 5]

Si bien podríamos construir los algoritmos para calcular las distancias mínimas para cada punto, R nos provee de librerías que nos facilitan la creación de estos modelos. Para ello, cargaremos la librería class, la cual nos permitirá ejecutar kNN rápidamente.

install.packages("class")

library(class)

Esta libreriá nos provee la función knn(), la cual tomará los datos de entrenamiento para crear el modelo y una vez creado el modelo tomará los datos de test para predecir el output para nuestra data de test.

iris_test_output_kNN <- knn(train = iris_entrena_input, 
                       cl = iris_entrena_output, 
                       test = iris_test_input, 
                       k = 3)

iris_test_output_kNN
#>  [1] versicolor versicolor versicolor versicolor setosa     versicolor
#>  [7] virginica  virginica  virginica  virginica  versicolor versicolor
#> [13] virginica  versicolor versicolor versicolor setosa     versicolor
#> [19] versicolor virginica  virginica  setosa     versicolor versicolor
#> [25] versicolor virginica  setosa     setosa     versicolor versicolor
#> [31] virginica  setosa     setosa     virginica  virginica  setosa    
#> [37] setosa     virginica  setosa     versicolor setosa     virginica 
#> [43] setosa     setosa     setosa     virginica  virginica  versicolor
#> [49] virginica  versicolor
#> Levels: setosa versicolor virginica

Asi, la función knn nos arroja la predicción solo con ingresarle como atributos la data de entrenamiento, los inputs del test y cuántos vecinos cercanos buscará (k). Y no solo eso, podemos comparar nuestra predicción con los output del test para ver qué tan exacto (accuracy en inglés) es nuestro modelo. Para ello calculamos el porcentaje de aciertos de la predicción respecto al output del test.

mean(iris_test_output_kNN == iris_test_output)
#> [1] 0.94

Además, podemos colocar un resumen en una tabla, también conocida como matriz de confusión, para ver cuántos valores predichos fueron iguales a los reales utilizando la función table().

table(iris_test_output_kNN, iris_test_output)
#>                     iris_test_output
#> iris_test_output_kNN setosa versicolor virginica
#>           setosa         14          0         0
#>           versicolor      0         18         2
#>           virginica       0          1        15

Intepretemos celda a celda este resultado:

1. Nuestro modelo kNN predijo 14 valores como especie “setosa” y resulta que en nuestro test el valor real, output era también setosa.
2. Nuestro modelo predijo 20 como especie versicolor. Sin embargo, en la data real-test, de esos 20, solo 18 son versicolor y 2 son virginica.
3. Nuestro modelo predijo 16 como especie virginica. Sin embargo, en la data real-test, de esos 16, solo 15 son virginica.

12.2.3 Diversos valores de k

Hasta el momento solo hemos utilizado un solo valor para k, 3 vecinos más cercanos. Sin embargo, podríamos ver la exactitud o accuracy para diferentes valores de k. Como tenemos 50 valores en nuestra data de entrenamiento veremos los aciertos tomando máximo 50 vecinos más cercanos.

k <- 1:50
resultado <- data.frame(k, precision = 0)

for(n in k){
  iris_test_output_kNN <- knn(train = iris_entrena_input, 
                              cl = iris_entrena_output, 
                              test = iris_test_input, 
                              k = n)
  
  resultado$precision[n] <- mean(iris_test_output_kNN == iris_test_output)
}

resultado %>% 
  ggplot() +
  aes(k, precision) +
  geom_line()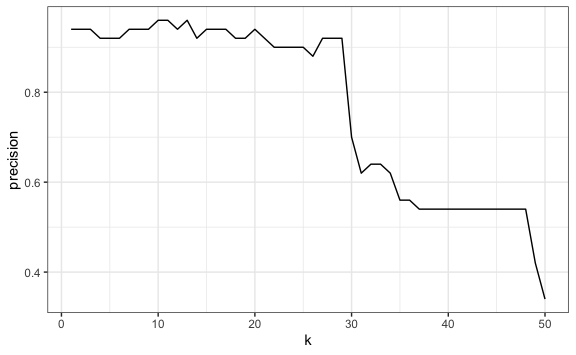

Como vemos, para este caso, a partir de cierto número de vecinos más cercanos el nivel de aciertos de nuestro algoritmo empieza a reducirse. Dependerá de cada caso el escoger el mejor “k” para nuestro modelo.

Ya hemos construido así nuestro primer modelo de machine learning.

12.3 Paquete caret

Ahora que ya hemos creado nuestro primer modelo de machine learning nos hemos visto con muchas líneas de código. Por ejemplo, para partir la muestra en entrenamiento y test, para calcular el “k” óptimo, etc. Para hacer el trabajo más sencillo usaremos la librería caret. Caret¹⁴ es un potente paquete que proporciona soporte para más de 230 algoritmos de machine learning. También proporciona excelentes funciones para muestrear los datos (para entrenamiento y test), preprocesamiento, creación del modelo, evaluación del modelo, etc.

install.packages('caret', dependencies = TRUE)
library(caret)

Vamos a hacer otro ejemplo con k vecinos más cercanos, pero ésta vez utilizando las funciones de la librería Caret. La data de este ejemplo la obtendremos de la librería ISLR, la cual contiene los porcentajes diarios de rendimiento para el índice bursátil S&P 500 entre el 2001 y 2005. Este data frame tiene 8 columnas que usaremos de input y la última columna que tiene dos clases (si sube o baja el índice) que usaremos como output (Ver ?Smarket).

install.packages("ISLR")

library(ISLR)
data(Smarket)
# Data frame que usaremos
Smarket %>% 
  head(10)
#>    Year   Lag1   Lag2   Lag3   Lag4   Lag5 Volume  Today Direction
#> 1  2001  0.381 -0.192 -2.624 -1.055  5.010 1.1913  0.959        Up
#> 2  2001  0.959  0.381 -0.192 -2.624 -1.055 1.2965  1.032        Up
#> 3  2001  1.032  0.959  0.381 -0.192 -2.624 1.4112 -0.623      Down
#> 4  2001 -0.623  1.032  0.959  0.381 -0.192 1.2760  0.614        Up
#> 5  2001  0.614 -0.623  1.032  0.959  0.381 1.2057  0.213        Up
#> 6  2001  0.213  0.614 -0.623  1.032  0.959 1.3491  1.392        Up
#> 7  2001  1.392  0.213  0.614 -0.623  1.032 1.4450 -0.403      Down
#> 8  2001 -0.403  1.392  0.213  0.614 -0.623 1.4078  0.027        Up
#> 9  2001  0.027 -0.403  1.392  0.213  0.614 1.1640  1.303        Up
#> 10 2001  1.303  0.027 -0.403  1.392  0.213 1.2326  0.287        Up

# Hacemos unas traducciones para facilitad del análisis
Smarket <- Smarket %>% 
  rename(Direccion = Direction) %>% 
  mutate(Direccion = ifelse(Direccion == "Up", "Sube", "Baja")) %>% 
  mutate_at(c("Direccion"), ~as.factor(.))

12.3.1 Creación de data de entrenamiento y test

Del total de nuestro data frame partiremos una parte de la data para entrenamiento y la otra para hacer los test. Para ello, caret nos ofrece la función createDataPartition(y = outcomes, p = proporcion, list = FALSE) la cual nos permitirá partir una proporción para entrenamiento y dejar el resto para testing. Vamos a destinar el 75% de los datos para entrenamiento y el atributo list lo dejamos en falso porque no queremos un objeto lista. El resultado de esta función es una serie de índices aleatorios, los cuales usaremos para construir nuestra data de entrenamiento y test.

set.seed(28)
indxEntrena <- createDataPartition(y = Smarket$Direccion, p = 0.75, list = FALSE)

SP_entrena <- Smarket[indxEntrena,]
SP_test <- Smarket[-indxEntrena,]

Esta función nos hace mucho más sencillo el muestro de datos y ya podríamos empezar a crear nuestro modelo.

12.3.2 Entrenando nuestro algoritmo de predicción

Para crear nuestro modelo de predicción y entrenarlo usaremos la función train() y especificaremos el atributo tuneLength = 20 para indicar que queremos que nos evalúe 20 diferentes valores para “k”. A diferencia de la función utilizada cuando construimos nuestro anterior modelo kNN, con caret no tenemos que separar los inputs de los outputs, sino lo ingresamos como un parámetro más de la función train().

set.seed(28)

SP_knnEntrenado <- train(Direccion ~ ., 
                data = SP_entrena, 
                method = "knn",  
                tuneLength = 20
                )

class(SP_knnEntrenado)
#> [1] "train"         "train.formula"

SP_knnEntrenado
#> k-Nearest Neighbors 
#> 
#> 938 samples
#>   8 predictor
#>   2 classes: 'Baja', 'Sube' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (25 reps) 
#> Summary of sample sizes: 938, 938, 938, 938, 938, 938, ... 
#> Resampling results across tuning parameters:
#> 
#>   k   Accuracy   Kappa    
#>    5  0.8317910  0.6625382
#>    7  0.8396091  0.6781770
#>    9  0.8429101  0.6847705
#>   11  0.8498168  0.6984716
#>   13  0.8484127  0.6955193
#>   15  0.8561378  0.7110835
#>   17  0.8584600  0.7157315
#>   19  0.8610032  0.7206949
#>   21  0.8598119  0.7183314
#>   23  0.8620446  0.7227893
#>   25  0.8666489  0.7321326
#>   27  0.8683517  0.7355501
#>   29  0.8668571  0.7324604
#>   31  0.8684517  0.7356510
#>   33  0.8695014  0.7377606
#>   35  0.8691338  0.7370225
#>   37  0.8702310  0.7392529
#>   39  0.8706310  0.7400393
#>   41  0.8734199  0.7456790
#>   43  0.8756463  0.7501696
#> 
#> Accuracy was used to select the optimal model using the largest value.
#> The final value used for the model was k = 43.

Vemos la exactitud (accuracy) para cada valor de “k” y el indicador Kappa. En el caso de Kappa no lo usaremos por el momento ya que es usado para problemas que tienen un desequilibrio en las clases (por ejemplo, división de 70-30 para los outcomes 0 y 1 y puede lograr una exactitud del 70% al predecir que todas las instancias son para el outcome 0).

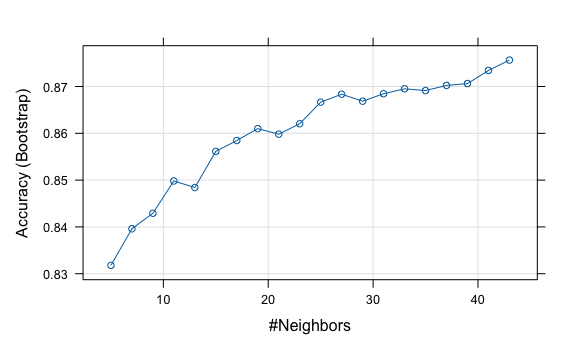
Así mismo, en la última línea tenemos el valor de “k” óptimo para este modelo. Además, nos encontramos con un nuevo tipo de objeto, el objeto train, el cual está listo para ingresarlo directamente a un gráfico usando la función plot().

plot(SP_knnEntrenado)

12.3.3 Ajuste de parámetros

Si bien ya podríamos probar nuestro modelo en la data de test nos vamos a detener a ajustar parámetros del modelo. Una de las partes más importantes del entrenamiento de modelos de Machine learning es ajustar los parámetros. Para ello usaremos la función trainControl para especificar una serie de parámetros en el modelo. El objeto que sale de trainControl se proporcionará como argumento para la función train que usaremos para entrenar.

SP_ctrl <- trainControl(method="cv", number = 5) 

Usaremos el método cv (Validación Cruzada) para indicar que vamos a partir nuestra data de entrenamiento en 5 partes iguales de forma aleatoria (5 fold en inglés). Luego, cada una de estas partes las vamos a utilizar como test para el modelo que creemos por las otras 4 partes. Es decir, usaremos parte de nuestra data de entrenamiento para testear nuestro modelo. Esto nos permitirá tomar el error promedio de los 5 test y obtener un dato más certero. Anteriormente no habíamos configurado este parámetro y dejado al valor por default. Por default el método es bootstrap el cual utiliza un método de muestreo con reemplazo a diferencia del cv que el muestro lo hace sin reemplazo.

Ahora, entrenemos nuestro modelo con los parámetros de control:

set.seed(28)

SP_knnEntrenado <- train(Direccion ~ ., 
                data = SP_entrena, 
                method = "knn",  
                tuneLength = 20,
                trControl = SP_ctrl
                )

12.3.4 Pre-procesando datos

Así mismo, un paso importante es pre-procesar la data, dado que, por ejemplo, los datos a diferentes escalas pueden alterar sustancialmente un algoritmo de aprendizaje. El método de escala (división por la desviación estándar) y el centrado (sustracción de la media) sons dos métodos muy frecuentes para poder pre-procesar los datos y obtener una mejor exactitud (ver ?preProcess).

set.seed(28)

SP_knnEntrenado <- train(Direccion ~ ., 
                data = SP_entrena, 
                method = "knn",  
                tuneLength = 20,
                trControl = SP_ctrl,
                preProcess = c("center","scale")
                )

SP_knnEntrenado
#> k-Nearest Neighbors 
#> 
#> 938 samples
#>   8 predictor
#>   2 classes: 'Baja', 'Sube' 
#> 
#> Pre-processing: centered (8), scaled (8) 
#> Resampling: Cross-Validated (5 fold) 
#> Summary of sample sizes: 751, 751, 750, 750, 750 
#> Resampling results across tuning parameters:
#> 
#>   k   Accuracy   Kappa    
#>    5  0.8667596  0.7324704
#>    7  0.8742235  0.7471798
#>    9  0.8753044  0.7495016
#>   11  0.8742007  0.7470650
#>   13  0.8806292  0.7600666
#>   15  0.8849073  0.7686722
#>   17  0.8795654  0.7579666
#>   19  0.8880817  0.7751289
#>   21  0.8891626  0.7773436
#>   23  0.8881044  0.7752995
#>   25  0.8902549  0.7794969
#>   27  0.8966378  0.7922259
#>   29  0.9008989  0.8007257
#>   31  0.8977017  0.7944032
#>   33  0.8966151  0.7921009
#>   35  0.9008761  0.8007176
#>   37  0.8955456  0.7899177
#>   39  0.8955399  0.7899431
#>   41  0.8965923  0.7921229
#>   43  0.8987200  0.7962878
#> 
#> Accuracy was used to select the optimal model using the largest value.
#> The final value used for the model was k = 29.

plot(SP_knnEntrenado)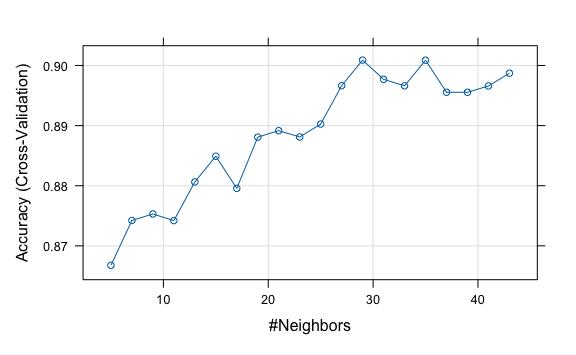

Vemos la mejora sustancial ahora que hemos ajustado algunos parámetros y hemos hecho que primero se reprocese. Tener en cuenta que cada vez que ajustamos parámetros el valor de “k” puede cambiar hasta encontrar al más óptimo. En este caso cambió a k = 29. Esto no quiere decir que a menor “k” el algoritmo es mejor, solo que es el más óptimo para este caso en particular con estos ajustes realizados.

12.3.5 Testeo del modelo de predicción

Ya tenemos nuestro modelo entrenado y listo para testearlo. Caret nos facilita realizar la predicción utilizando la función predict(modelo, newdata = data_de_test)

SP_knnPrediccion <- predict(SP_knnEntrenado, newdata = SP_test )

SP_knnPrediccion %>% 
  head(50)
#>  [1] Sube Sube Baja Baja Sube Sube Baja Sube Baja Baja Baja Baja Sube Sube Sube
#> [16] Baja Sube Baja Baja Baja Sube Baja Sube Sube Baja Baja Sube Baja Sube Sube
#> [31] Baja Sube Baja Baja Baja Sube Sube Baja Baja Baja Baja Sube Sube Sube Baja
#> [46] Sube Sube Baja Baja Sube
#> Levels: Baja Sube

Si queremos ir aun más allá, para comprender mejor cómo operan estos algoritmos de machine learning, podemos obtener el resultado de la predicción antes de indicar qué clase le asigna el modelo. Para ello utilizamos la misma función predict() pero esta vez modificamos el atributo type. Por default type = "raw" mostrándonos la clase predicha, pero el resultado real es un conjunto de probabilidades. El modelo calcula internamente qué tan probable es que sea de una u otra clase (Baja o Sube).

Mostremos las probabilidades en vez de la clase.

prob_knnPrediccion <- predict(SP_knnEntrenado, newdata = SP_test, type = "prob")

prob_knnPrediccion %>% 
  head(10)
#>          Baja       Sube
#> 1  0.24137931 0.75862069
#> 2  0.37931034 0.62068966
#> 3  0.62068966 0.37931034
#> 4  0.96551724 0.03448276
#> 5  0.31034483 0.68965517
#> 6  0.44827586 0.55172414
#> 7  0.93103448 0.06896552
#> 8  0.06896552 0.93103448
#> 9  0.55172414 0.44827586
#> 10 1.00000000 0.00000000

Como vemos, para cada valor del test el modelo nos calcula la probabilidad que estima de que Baje y la probabilidad de Suba el índice S&P. El algoritmo por default nos da la clase que tiene más de 50% de probabilidad.

Ya tenemos el objeto SP_knnPrediccion con los valores predichos. Si queremos calcular la exactitud del modelo (accuracy) utilizaremos la función confusionMatrix(data_prediccion, output_real) la cual no solo nos reporta la matriz de confusión, sino también una serie de mediciones de la presición de nuestro modelo.

confusionMatrix(SP_knnPrediccion, SP_test$Direccion)
#> Confusion Matrix and Statistics
#> 
#>           Reference
#> Prediction Baja Sube
#>       Baja  129    4
#>       Sube   21  158
#>                                          
#>                Accuracy : 0.9199         
#>                  95% CI : (0.884, 0.9475)
#>     No Information Rate : 0.5192         
#>     P-Value [Acc > NIR] : < 2.2e-16      
#>                                          
#>                   Kappa : 0.8388         
#>                                          
#>  Mcnemar's Test P-Value : 0.001374       
#>                                          
#>             Sensitivity : 0.8600         
#>             Specificity : 0.9753         
#>          Pos Pred Value : 0.9699         
#>          Neg Pred Value : 0.8827         
#>              Prevalence : 0.4808         
#>          Detection Rate : 0.4135         
#>    Detection Prevalence : 0.4263         
#>       Balanced Accuracy : 0.9177         
#>                                          
#>        'Positive' Class : Baja           
#> 

Obtenemos casi 91.99% de exactitud (accuracy), así como un intervalo de confianza del 95% de esta exactitud.

12.4 Matriz de confusión

Ya hemos utilizado matrices de confusión en nuestros dos ejemplos anteriores. Ahora nos toca entender propiamente su definición así como algunas de las métricas de evaluación de esta matriz.

Una matriz de confusión, también conocida como matriz de error, nos permite la visualización del rendimiento de un algoritmo, generalmente uno de aprendizaje supervisado (en el aprendizaje no supervisado generalmente se denomina matriz coincidente). Cada fila de la matriz representa las instancias en una clase predicha, mientras que cada columna representa las instancias en una clase real (o viceversa). El nombre se deriva del hecho de que hace que sea fácil ver si el sistema confunde dos clases (es decir, comúnmente etiquetar incorrectamente una como otra).

Las clasificaciones binarias, cuando el outcome puede tomar solo dos clases, nos arrojan esta siguiente matriz de confusión.

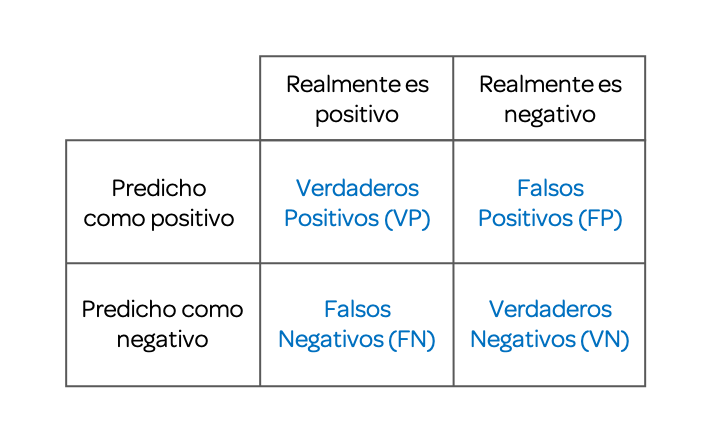
12.4.1 exactitud

Ya hemos venido utilizando este término en nuestros ejemplos. La exactitud del modelo (accuracy en inglés), la podemos calcular a partir de la matriz de confusión:

\(Accuracy=\frac{VP+VN}{VP+VN+FP+FN}\)

El accuracy del modelo es la proporción de veces que el algoritmo predijo correctamente, respecto al total de datos evaluados.

12.4.2 Sensitividad

La sensibilidad (también llamada tasa positiva verdadera, el recuerdo o la probabilidad de detección en algunos campos) mide la proporción de positivos reales que se identifican correctamente como tales (por ejemplo, el porcentaje de personas enfermas que se identifican correctamente como que tienen condición).

\(Sensitivity=\frac{VP}{VP+FN}\)

12.4.3 Especificidad

La especificidad (también llamada tasa negativa verdadera) mide la proporción de negativos reales que se identifican correctamente como tales (por ejemplo, el porcentaje de personas sanas que se identifican correctamente como que no tienen la afección).

\(Specificity=\frac{VN}{VN+FP}\)

12.5 Ejercicios

111. Utilizando la librería caret, particiona el data frame iris de tal forma de tener 70% de datos de entrenamiento y 30% de datos de prueba.

Solución

index_entrena <- createDataPartition(y = iris$Species, p = 0.7, list = FALSE)

iris2_entrena <- iris[index_entrena, ]
iris2_test <- iris[-index_entrena, ]

112. Utilizando la librería caret y los datos de entrenamiento obtenidos en el ejercicio anterior, crea un modelo de k-vecino más cercano. Plotea el resultado del objeto de entrenamiento.

Solución

iris2_ctrl <- trainControl(method="cv", number = 5) 

iris2_knnEntrenado <- train(Species ~ ., 
                data = iris2_entrena, 
                method = "knn",  
                tuneLength = 20,
                trControl = iris2_ctrl,
                preProcess = c("center","scale")
                )

iris2_knnEntrenado

plot(iris2_knnEntrenado)

113. Utiliza el modelo creado en el ejercicio anterior para predecir los outputs del objeto test. Reporta la matriz de confusión.

Solución

iris2_knnPrediccion <- predict(iris2_knnEntrenado, newdata = iris2_test )

confusionMatrix(iris2_knnPrediccion, iris2_test$Species)

12.6 Regresión lineal simple

Ahora nos toca predecir sobre variables continuas, los algoritmos de supervisión para estos casos son llamados regresión.

Para entender regresión lineal vamos a iniciar con un ejemplo con una sola variable como input, a ello se le conoce como Regresión lineal simple. Para ello vamos a utilizar data de la librería HistData donde encontraremos un conjunto de datos que enumeran las observaciones individuales de 934 niños en 205 familias almacenadas en el objeto GaltonFamilies.

install.packages("HistData")

library(HistData)
data(GaltonFamilies)

# Hacemos algunos filtros para tener un papá y un hijo por familia
alturas <- GaltonFamilies %>%
  filter(gender == "male") %>%
  group_by(family) %>%
  sample_n(1) %>% # muestra aleatoria de 1 hijo por familia
  ungroup() %>%
  select(father, childHeight) %>%
  rename(hijo = childHeight, papa = father) %>% 
  mutate(papa = papa/39.37) %>% # De pulgadas a metros
  mutate(hijo = hijo/39.37) # De pulgadas a metros

Visualmente podríamos ver si hay una relación entre las alturas de papá e hijo:

alturas %>% 
  ggplot() +
  aes(papa, hijo) +
  geom_point() +
  geom_abline(lty = 2)

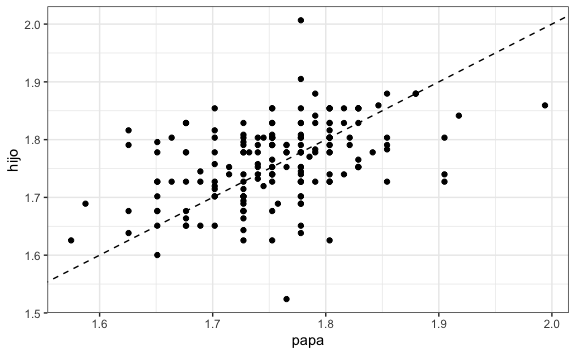
Como vemos, hay una correlación positiva, de tal forma que mientras más alto el padre el hijo llega a tener una mayor altura de adulto. Esta línea, sin embargo, no es más que una línea por default. El reto está en encontrar cuál es le línea que minimiza la distancia de los puntos a esta línea, conocido como minimización del error.

Podríamos intentar predecir la estatura que tendrá el hijo a partir de la estatura del padre usando la ecuación de esta recta:

\(Y = \beta_0+\beta_1X\)

Donde \(X\) es una variable independiente, explicativa, en este caso la estatura del papá. \(\beta_1\) es un parámetro que mide la influencia que la variable explicativa tiene sobre la variable dependiente \(Y\) y \(\beta_0\) es la intersección o término constante. En nuestro caso, la estatura del hijo.

En estadística, la regresión lineal o ajuste lineal es un modelo matemático usado para aproximar la relación de dependencia entre una variable dependiente \(Y\) y las variables independientes \(X_i\).

Así, nuestro problema se reduce a entrenar a nuestro modelo para que encuentre los valores de a intersección, \(\beta_0\), y el valor del parámetro que acompaña a \(X_1\), \(\beta_1\), para luego utilizar estos datos como predicción en nuestra data de test.

index_entrena <- createDataPartition(alturas$hijo, p = 0.5, list = FALSE)

alturas_entrena <- alturas[index_entrena, ]
alturas_test <- alturas[-index_entrena, ]

Ahora que ya tenemos nuestra data podemos entrenar nuestro modelo.

alturas_ctrl <- trainControl(method="cv", number = 10)

alturas_lmEntrenado <- train(hijo ~ ., 
                data = alturas_entrena, 
                method = "lm",
                trControl = alturas_ctrl
                )

alturas_lmEntrenado
#> Linear Regression 
#> 
#> 91 samples
#>  1 predictor
#> 
#> No pre-processing
#> Resampling: Cross-Validated (10 fold) 
#> Summary of sample sizes: 81, 82, 81, 81, 83, 82, ... 
#> Resampling results:
#> 
#>   RMSE        Rsquared   MAE       
#>   0.06076013  0.2477919  0.04941711
#> 
#> Tuning parameter 'intercept' was held constant at a value of TRUE

Vemos como resultados principales el RMSE, que son las siglas en inglés de error cuadrático medio, y es el valor que la regresión lineal buscar minimizar. Además, tenemos el Rsquared, R cuadrado o \(R^2\), que es el coeficiente de determinación el cual determina la calidad del modelo para replicar los resultados. Mientras más alto y cercano a 1 es mejor la calidad del modelo.

Finalmente, dado que ya tenemos el modelo entrenado podemos predecir los valores, que no sería más que evaluar la ecuación con los valores de la data de test. Además, como mencionamos, en regresión buscamos reducir el error cuadrático medio, RMSE. Entonces, calcularemos el RMSE para la data predicha vs la data de test.

# Predicción:
alturas_lmPrediccion <- predict(alturas_lmEntrenado, newdata = alturas_test )

# Cálculo del error
error <- alturas_lmPrediccion - alturas_test$hijo

# Cálculo del error cuadrático medio RMSE:
sqrt(mean(error^2))
#> [1] 0.06190904

Si deseamos también podemos reportar los coeficientes de la ecuación y visualizarlos:

\(Y = \beta_0+\beta_1X\)

alturas_lmEntrenado$finalModel$coefficients
#> (Intercept)        papa 
#>   1.0387526   0.4119603

intercepcion <- alturas_lmEntrenado$finalModel$coefficients[1]
pendiente <- alturas_lmEntrenado$finalModel$coefficients[2]

#Visualización
alturas %>% 
  ggplot() +
  aes(papa, hijo) +
  geom_point() +
  geom_abline(lty = 2, intercept = intercepcion, slope = pendiente, color = "red")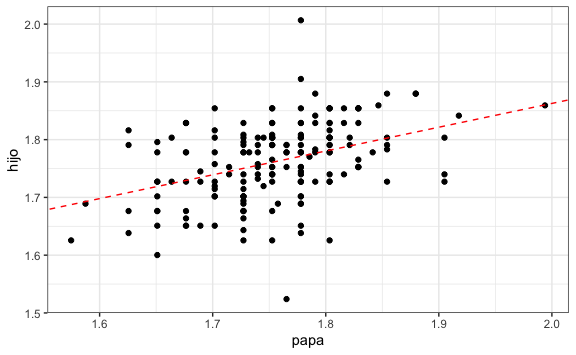

12.7 Regresión lineal múltiple

Ahora que ya conocemos la regresión lineal podemos ejecutar un modelo de regresión lineal múltiple, el cual involucra a más de 1 variable como input. Para ello, utilizaremos el dataset diamonds que contiene los precios y otros atributos de casi 54,000 diamantes.

library(ggplot2)
data("diamonds")

diamonds <- diamonds %>% 
  rename(precio = price)

diamonds %>% 
  head(10)
#> # A tibble: 10 × 10
#>    carat cut       color clarity depth table precio     x     y     z
#>    <dbl> <ord>     <ord> <ord>   <dbl> <dbl>  <int> <dbl> <dbl> <dbl>
#>  1  0.23 Ideal     E     SI2      61.5    55    326  3.95  3.98  2.43
#>  2  0.21 Premium   E     SI1      59.8    61    326  3.89  3.84  2.31
#>  3  0.23 Good      E     VS1      56.9    65    327  4.05  4.07  2.31
#>  4  0.29 Premium   I     VS2      62.4    58    334  4.2   4.23  2.63
#>  5  0.31 Good      J     SI2      63.3    58    335  4.34  4.35  2.75
#>  6  0.24 Very Good J     VVS2     62.8    57    336  3.94  3.96  2.48
#>  7  0.24 Very Good I     VVS1     62.3    57    336  3.95  3.98  2.47
#>  8  0.26 Very Good H     SI1      61.9    55    337  4.07  4.11  2.53
#>  9  0.22 Fair      E     VS2      65.1    61    337  3.87  3.78  2.49
#> 10  0.23 Very Good H     VS1      59.4    61    338  4     4.05  2.39

Partimos la data en dos tomando 70% de data para entrenamiento:

index_entrena <- createDataPartition(diamonds$precio, p = 0.7, list = FALSE)

diamantes_entrena <- diamonds[index_entrena, ]
diamantes_test <- diamonds[-index_entrena, ]

Creamos ahora nuestro modelo de regresión lineal múltiple y reportamos tanto los resultados del error como los coeficientes de la ecuación lineal.

diamantes_ctrl <- trainControl(method="cv", number = 10)

diamantes_lmEntrenado <- train(precio ~ ., 
                diamantes_entrena, 
                method = "lm",
                trControl = diamantes_ctrl
                )

diamantes_lmEntrenado
#> Linear Regression 
#> 
#> 37759 samples
#>     9 predictor
#> 
#> No pre-processing
#> Resampling: Cross-Validated (10 fold) 
#> Summary of sample sizes: 33983, 33984, 33983, 33983, 33983, 33983, ... 
#> Resampling results:
#> 
#>   RMSE      Rsquared   MAE     
#>   1127.149  0.9200345  737.5332
#> 
#> Tuning parameter 'intercept' was held constant at a value of TRUE

diamantes_lmEntrenado$finalModel$coefficients
#> (Intercept)       carat       cut.L       cut.Q       cut.C     `cut^4` 
#>  6033.33693 11432.25964   578.85759  -304.78440   149.25375   -17.73461 
#>     color.L     color.Q     color.C   `color^4`   `color^5`   `color^6` 
#> -1944.34903  -671.51207  -153.34540    49.34632   -88.31014   -44.29660 
#>   clarity.L   clarity.Q   clarity.C `clarity^4` `clarity^5` `clarity^6` 
#>  4012.86187 -1875.53117   930.61616  -341.20511   208.50985    20.15169 
#> `clarity^7`       depth       table           x           y           z 
#>    85.80580   -62.67254   -27.71926 -1059.07717    12.73836   -86.94498

Vemos que nos da el RMSE y un R cuadrado bastante cercano a 1, el cual nos denota una alta calidad del modelo para replicar los resultados.

Utilicemos nuestro modelo para predecir los precios de la data de test.

# Predicción:
diamantes_lmPrediccion <- predict(diamantes_lmEntrenado, newdata = diamantes_test )

# Cálculo del error
error <- diamantes_lmPrediccion - diamantes_test$precio

# Cálculo del error cuadrático medio RMSE:
sqrt(mean(error^2))
#> [1] 1141.211

Así, hemos aprendido a realizar un modelo más de machine learning: el de regresión lineal, tanto simple como múltiple.

12.8 Método estándar para evaluar exactitud

Ahora que ya conocemos cómo construir modelos aplicaremos métricas que nos permiten una mejor exactitud en los modelos de clasificación para dos clases.

Para esto recordemos los resultados del modelo que creamos usando el algoritmo de k-vecinos más próximos para predecir si sube o baja el índice S&P.

SP_knnEntrenado
#> k-Nearest Neighbors 
#> 
#> 938 samples
#>   8 predictor
#>   2 classes: 'Baja', 'Sube' 
#> 
#> Pre-processing: centered (8), scaled (8) 
#> Resampling: Cross-Validated (5 fold) 
#> Summary of sample sizes: 751, 751, 750, 750, 750 
#> Resampling results across tuning parameters:
#> 
#>   k   Accuracy   Kappa    
#>    5  0.8667596  0.7324704
#>    7  0.8742235  0.7471798
#>    9  0.8753044  0.7495016
#>   11  0.8742007  0.7470650
#>   13  0.8806292  0.7600666
#>   15  0.8849073  0.7686722
#>   17  0.8795654  0.7579666
#>   19  0.8880817  0.7751289
#>   21  0.8891626  0.7773436
#>   23  0.8881044  0.7752995
#>   25  0.8902549  0.7794969
#>   27  0.8966378  0.7922259
#>   29  0.9008989  0.8007257
#>   31  0.8977017  0.7944032
#>   33  0.8966151  0.7921009
#>   35  0.9008761  0.8007176
#>   37  0.8955456  0.7899177
#>   39  0.8955399  0.7899431
#>   41  0.8965923  0.7921229
#>   43  0.8987200  0.7962878
#> 
#> Accuracy was used to select the optimal model using the largest value.
#> The final value used for the model was k = 29.

En la penúltima línea se puede leer que la exactitud (accuracy) fue usada para seleccionar el modelo más óptimo usando el valor más grande. Sin embargo, esta no es la única forma de determinar cuál es el modelo más óptimo.

Recordemos cómo se calcula por default la exactitud (accuracy), hemos utilizado la regla simple de que si la probabilidad de que sea de una determinada clase es más de 50% entonces se le asigne esa clase y luego calculamos la proporción de aciertos entre el total de casos.

Sin embargo, no tiene que ser 50%, podríamos ser más exigentes e indicar que si la probabilidad es mayor del 60% u 80% entonces se le asigna una determinada clase. Vemos que hay diferentes probabilidades y ello nos daría diferentes accuracy.

Es así como surge el indicador del área bajo la curva de Característica Operativa del Receptor, ROC por sus siglas en inglés (Fawcett 2005). Este indicador nos mide qué tan bien puede distinguir un modelo entre dos clases y es considerado el método estándar para evaluar la exactitud de los modelos de distribución predictiva (Jorge M. Lobo 2007) y calcula las exactitudes no solo para cuando discriminamos a partir del 50%, sino para más valores de probabilidad.

Para utilizar esta métrica modificaremos nuestros parámetros de control agregando tres atributos que permitirán calcular el ROC.

SP2_ctrl <- trainControl(
  method="cv",
  number = 5,
  savePredictions = TRUE, # Guardamos las predicciones en cada iteración
  classProb = TRUE, # Calculamos las probabilidades de ocurrencia
  summaryFunction = twoClassSummary # Hacemos explícito que son dos clases
)

Con estos parámetros modificados procederemos a volver a entrenar a nuestro modelo.

set.seed(28)

SP2_knnEntrenado <- train(Direccion ~ ., 
                data = SP_entrena, # Misma data de entrenamiento para modelo SP2
                method = "knn",  
                tuneLength = 20,
                trControl = SP2_ctrl,
                preProcess = c("center","scale"),
                metric = "ROC"
                )

SP2_knnEntrenado
#> k-Nearest Neighbors 
#> 
#> 938 samples
#>   8 predictor
#>   2 classes: 'Baja', 'Sube' 
#> 
#> Pre-processing: centered (8), scaled (8) 
#> Resampling: Cross-Validated (5 fold) 
#> Summary of sample sizes: 751, 751, 750, 750, 750 
#> Resampling results across tuning parameters:
#> 
#>   k   ROC        Sens       Spec     
#>    5  0.9356332  0.8295482  0.9012203
#>    7  0.9491333  0.8229060  0.9217757
#>    9  0.9581705  0.8295971  0.9176941
#>   11  0.9581360  0.8162882  0.9279402
#>   13  0.9637686  0.8274481  0.9300021
#>   15  0.9628994  0.8340904  0.9320640
#>   17  0.9621501  0.8296947  0.9258784
#>   19  0.9642725  0.8429304  0.9299811
#>   21  0.9663917  0.8473504  0.9278982
#>   23  0.9670048  0.8473993  0.9258153
#>   25  0.9694807  0.8452259  0.9320219
#>   27  0.9714313  0.8452015  0.9443720
#>   29  0.9731740  0.8451282  0.9526404
#>   31  0.9724945  0.8473260  0.9443930
#>   33  0.9710535  0.8406838  0.9484957
#>   35  0.9716720  0.8495482  0.9484957
#>   37  0.9710530  0.8362393  0.9505365
#>   39  0.9738171  0.8384615  0.9484957
#>   41  0.9739988  0.8407082  0.9484746
#>   43  0.9739789  0.8362637  0.9567221
#> 
#> ROC was used to select the optimal model using the largest value.
#> The final value used for the model was k = 41.

Vemos que ahora ROC fue utilizado para seleccionar el modelo más óptimo. Mientras más cercano el valor de ROC sea a 1 mejor será nuestro modelo. Con este modelo podemos predecir los valores a partir de la data de test.

SP2_knnPrediccion <- predict(SP2_knnEntrenado, newdata = SP_test )

confusionMatrix(SP2_knnPrediccion, SP_test$Direccion)
#> Confusion Matrix and Statistics
#> 
#>           Reference
#> Prediction Baja Sube
#>       Baja  132    3
#>       Sube   18  159
#>                                          
#>                Accuracy : 0.9327         
#>                  95% CI : (0.899, 0.9579)
#>     No Information Rate : 0.5192         
#>     P-Value [Acc > NIR] : < 2e-16        
#>                                          
#>                   Kappa : 0.8647         
#>                                          
#>  Mcnemar's Test P-Value : 0.00225        
#>                                          
#>             Sensitivity : 0.8800         
#>             Specificity : 0.9815         
#>          Pos Pred Value : 0.9778         
#>          Neg Pred Value : 0.8983         
#>              Prevalence : 0.4808         
#>          Detection Rate : 0.4231         
#>    Detection Prevalence : 0.4327         
#>       Balanced Accuracy : 0.9307         
#>                                          
#>        'Positive' Class : Baja           
#> 

Vemos cómo nuestra exactitud (accuracy) ha incrementado de 91.99% a 93.27%. Ésta métrica es muy recomendada para mejorar la exactitud de nuestro modelo, además que nos permite más fácilmente utilizarlo como comparador entre diferentes modelos que podamos crear.

12.9 Selección de modelo más óptimo

Hemos aprendido cómo crear algunos modelos de machine learning. Como nos debemos de haber percatado, con caret seguimos el mismo patrón para la partición, entrenamiento y predicción. La variación está en el cómo pre-procesar los datos y el ajuste de parámetros. Podríamos así crear múltiples modelos, pero finalmente tenemos que elegir uno el cual nos servirá para hacer nuestras predicciones.

En esta sección, vamos a comparar diferentes modelos predictivos aceptando sus valores por default y elegiremos el mejor usando las herramientas presentadas en las secciones anteriores.

Para ello, vamos a utilizar un nuevo caso. Ésta vez estamos evaluando el comportamiento de nuestros 5,000 clientes, algunos de los cuales se han dado de baja de nuestros servicios. Tenemos 19 predictores, la mayoría de ellos numéricos, en el dataset mlc_churn. Para acceder a la data tenemos que cargar la librería modeldata.

install.packages("modeldata")
library(modeldata)

data(mlc_churn)

str(mlc_churn)
#> tibble [5,000 × 20] (S3: tbl_df/tbl/data.frame)
#>  $ state                        : Factor w/ 51 levels "AK","AL","AR",..: 17 36 32 36 37 2 20 25 19 50 ...
#>  $ account_length               : int [1:5000] 128 107 137 84 75 118 121 147 117 141 ...
#>  $ area_code                    : Factor w/ 3 levels "area_code_408",..: 2 2 2 1 2 3 3 2 1 2 ...
#>  $ international_plan           : Factor w/ 2 levels "no","yes": 1 1 1 2 2 2 1 2 1 2 ...
#>  $ voice_mail_plan              : Factor w/ 2 levels "no","yes": 2 2 1 1 1 1 2 1 1 2 ...
#>  $ number_vmail_messages        : int [1:5000] 25 26 0 0 0 0 24 0 0 37 ...
#>  $ total_day_minutes            : num [1:5000] 265 162 243 299 167 ...
#>  $ total_day_calls              : int [1:5000] 110 123 114 71 113 98 88 79 97 84 ...
#>  $ total_day_charge             : num [1:5000] 45.1 27.5 41.4 50.9 28.3 ...
#>  $ total_eve_minutes            : num [1:5000] 197.4 195.5 121.2 61.9 148.3 ...
#>  $ total_eve_calls              : int [1:5000] 99 103 110 88 122 101 108 94 80 111 ...
#>  $ total_eve_charge             : num [1:5000] 16.78 16.62 10.3 5.26 12.61 ...
#>  $ total_night_minutes          : num [1:5000] 245 254 163 197 187 ...
#>  $ total_night_calls            : int [1:5000] 91 103 104 89 121 118 118 96 90 97 ...
#>  $ total_night_charge           : num [1:5000] 11.01 11.45 7.32 8.86 8.41 ...
#>  $ total_intl_minutes           : num [1:5000] 10 13.7 12.2 6.6 10.1 6.3 7.5 7.1 8.7 11.2 ...
#>  $ total_intl_calls             : int [1:5000] 3 3 5 7 3 6 7 6 4 5 ...
#>  $ total_intl_charge            : num [1:5000] 2.7 3.7 3.29 1.78 2.73 1.7 2.03 1.92 2.35 3.02 ...
#>  $ number_customer_service_calls: int [1:5000] 1 1 0 2 3 0 3 0 1 0 ...
#>  $ churn                        : Factor w/ 2 levels "yes","no": 2 2 2 2 2 2 2 2 2 2 ...

# Traducimos outputs
mlc_churn <- mlc_churn %>% 
  rename(de_baja = churn) %>% 
  mutate(de_baja = ifelse(de_baja == "yes", "Sí", "No")) %>% 
  mutate(de_baja = as.factor(de_baja))
  
# Proporción de "Sí" y "No"s:
prop.table(table(mlc_churn$de_baja))
#> 
#>     No     Sí 
#> 0.8586 0.1414

Creamos ahora nuestra de entrenamiento y de test, 70% entrenamiento.

set.seed(28)
index_entrena <- createDataPartition(mlc_churn$de_baja, p = 0.7, list = FALSE)

churn_entrena <- mlc_churn[index_entrena, ]
churn_test <- mlc_churn[-index_entrena, ]

Hasta aquí hemos hecho exactamente el mismo paso que en los modelos anteriores. Sin embargo, anteriormente hemos especificado el método cross-validation dentro de nuestros parámetros de control y como recordaremos este método parte nuestra data en n partes seleccionadas aleatoriamente (folds). Ahora no necesitamos que sean aleatoriamente para cada modelo, sino los mismos folds.

Así, crearemos manualmente una lista de 5 folds utilizando la función createFolds(outputs, numero_folds).

set.seed(28)
folds_manual <- createFolds(churn_entrena$de_baja, k = 5)
str(folds_manual)
#> List of 5
#>  $ Fold1: int [1:701] 1 3 8 19 29 49 61 63 65 72 ...
#>  $ Fold2: int [1:700] 2 5 17 27 30 31 41 48 55 56 ...
#>  $ Fold3: int [1:700] 11 13 20 23 28 34 36 38 39 46 ...
#>  $ Fold4: int [1:700] 6 7 9 10 12 14 16 18 22 32 ...
#>  $ Fold5: int [1:700] 4 15 21 24 25 26 33 35 37 40 ...

Utilizaremos la métrica ROC para todos los modelos. Además, agregraremos el atributo index donde ingresaremos como atributo los folds creados.

churn_ctrl <- trainControl(
  savePredictions = TRUE,
  classProb = TRUE, 
  summaryFunction = twoClassSummary,
  index = folds_manual # Lista con elementos para cada iteración
)

El siguiente sería elegir los algoritmos de machine learning que queremos utilizar para crear nuestros modelos. Caret nos provee más de 230 algoritmos que se pueden listar utilizando la función getModelInfo(), la cual nos hace un llamado a la lista total de algoritmos. Usaremos names() para obtener solo los nombres.

names(getModelInfo())
#>   [1] "ada"                 "AdaBag"              "AdaBoost.M1"        
#>   [4] "adaboost"            "amdai"               "ANFIS"              
#>   [7] "avNNet"              "awnb"                "awtan"              
#>  [10] "bag"                 "bagEarth"            "bagEarthGCV"        
#>  [13] "bagFDA"              "bagFDAGCV"           "bam"                
#>  [16] "bartMachine"         "bayesglm"            "binda"              
#>  [19] "blackboost"          "blasso"              "blassoAveraged"     
#>  [22] "bridge"              "brnn"                "BstLm"              
#>  [25] "bstSm"               "bstTree"             "C5.0"               
#>  [28] "C5.0Cost"            "C5.0Rules"           "C5.0Tree"           
#>  [31] "cforest"             "chaid"               "CSimca"             
#>  [34] "ctree"               "ctree2"              "cubist"             
#>  [37] "dda"                 "deepboost"           "DENFIS"             
#>  [40] "dnn"                 "dwdLinear"           "dwdPoly"            
#>  [43] "dwdRadial"           "earth"               "elm"                
#>  [46] "enet"                "evtree"              "extraTrees"         
#>  [49] "fda"                 "FH.GBML"             "FIR.DM"             
#>  [52] "foba"                "FRBCS.CHI"           "FRBCS.W"            
#>  [55] "FS.HGD"              "gam"                 "gamboost"           
#>  [58] "gamLoess"            "gamSpline"           "gaussprLinear"      
#>  [61] "gaussprPoly"         "gaussprRadial"       "gbm_h2o"            
#>  [64] "gbm"                 "gcvEarth"            "GFS.FR.MOGUL"       
#>  [67] "GFS.LT.RS"           "GFS.THRIFT"          "glm.nb"             
#>  [70] "glm"                 "glmboost"            "glmnet_h2o"         
#>  [73] "glmnet"              "glmStepAIC"          "gpls"               
#>  [76] "hda"                 "hdda"                "hdrda"              
#>  [79] "HYFIS"               "icr"                 "J48"                
#>  [82] "JRip"                "kernelpls"           "kknn"               
#>  [85] "knn"                 "krlsPoly"            "krlsRadial"         
#>  [88] "lars"                "lars2"               "lasso"              
#>  [91] "lda"                 "lda2"                "leapBackward"       
#>  [94] "leapForward"         "leapSeq"             "Linda"              
#>  [97] "lm"                  "lmStepAIC"           "LMT"                
#> [100] "loclda"              "logicBag"            "LogitBoost"         
#> [103] "logreg"              "lssvmLinear"         "lssvmPoly"          
#> [106] "lssvmRadial"         "lvq"                 "M5"                 
#> [109] "M5Rules"             "manb"                "mda"                
#> [112] "Mlda"                "mlp"                 "mlpKerasDecay"      
#> [115] "mlpKerasDecayCost"   "mlpKerasDropout"     "mlpKerasDropoutCost"
#> [118] "mlpML"               "mlpSGD"              "mlpWeightDecay"     
#> [121] "mlpWeightDecayML"    "monmlp"              "msaenet"            
#> [124] "multinom"            "mxnet"               "mxnetAdam"          
#> [127] "naive_bayes"         "nb"                  "nbDiscrete"         
#> [130] "nbSearch"            "neuralnet"           "nnet"               
#> [133] "nnls"                "nodeHarvest"         "null"               
#> [136] "OneR"                "ordinalNet"          "ordinalRF"          
#> [139] "ORFlog"              "ORFpls"              "ORFridge"           
#> [142] "ORFsvm"              "ownn"                "pam"                
#> [145] "parRF"               "PART"                "partDSA"            
#> [148] "pcaNNet"             "pcr"                 "pda"                
#> [151] "pda2"                "penalized"           "PenalizedLDA"       
#> [154] "plr"                 "pls"                 "plsRglm"            
#> [157] "polr"                "ppr"                 "pre"                
#> [160] "PRIM"                "protoclass"          "qda"                
#> [163] "QdaCov"              "qrf"                 "qrnn"               
#> [166] "randomGLM"           "ranger"              "rbf"                
#> [169] "rbfDDA"              "Rborist"             "rda"                
#> [172] "regLogistic"         "relaxo"              "rf"                 
#> [175] "rFerns"              "RFlda"               "rfRules"            
#> [178] "ridge"               "rlda"                "rlm"                
#> [181] "rmda"                "rocc"                "rotationForest"     
#> [184] "rotationForestCp"    "rpart"               "rpart1SE"           
#> [187] "rpart2"              "rpartCost"           "rpartScore"         
#> [190] "rqlasso"             "rqnc"                "RRF"                
#> [193] "RRFglobal"           "rrlda"               "RSimca"             
#> [196] "rvmLinear"           "rvmPoly"             "rvmRadial"          
#> [199] "SBC"                 "sda"                 "sdwd"               
#> [202] "simpls"              "SLAVE"               "slda"               
#> [205] "smda"                "snn"                 "sparseLDA"          
#> [208] "spikeslab"           "spls"                "stepLDA"            
#> [211] "stepQDA"             "superpc"             "svmBoundrangeString"
#> [214] "svmExpoString"       "svmLinear"           "svmLinear2"         
#> [217] "svmLinear3"          "svmLinearWeights"    "svmLinearWeights2"  
#> [220] "svmPoly"             "svmRadial"           "svmRadialCost"      
#> [223] "svmRadialSigma"      "svmRadialWeights"    "svmSpectrumString"  
#> [226] "tan"                 "tanSearch"           "treebag"            
#> [229] "vbmpRadial"          "vglmAdjCat"          "vglmContRatio"      
#> [232] "vglmCumulative"      "widekernelpls"       "WM"                 
#> [235] "wsrf"                "xgbDART"             "xgbLinear"          
#> [238] "xgbTree"             "xyf"

A continuación, crearemos una serie de modelos con los datos de entrenamiento y nuestros parámetros de control utilizando los algoritmos más utilizados en machine learning. Así mismo, utilizaremos la métrica de rendimiento ROC en vez de accuracy para comparar los modelos.

12.9.1 Modelo de los k-vecinos más cercanos

Si bien es muy modelo simple también es muy útil. Empecemos con este modelo que ya aprendimos a crear durante este capítulo.

churn_modelo_knn <- train(de_baja ~ .,
                   churn_entrena,
                   metric = "ROC",
                   method = "knn",
                   tuneLength = 20,
                   trControl = churn_ctrl)
churn_modelo_knn
#> k-Nearest Neighbors 
#> 
#> 3501 samples
#>   19 predictor
#>    2 classes: 'No', 'Sí' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (5 reps) 
#> Summary of sample sizes: 701, 700, 700, 700, 700 
#> Resampling results across tuning parameters:
#> 
#>   k   ROC        Sens       Spec      
#>    5  0.6607479  0.9805389  0.21767677
#>    7  0.6713682  0.9877748  0.19747475
#>    9  0.6816558  0.9924321  0.17222222
#>   11  0.6864001  0.9938458  0.16161616
#>   13  0.6874802  0.9947607  0.14040404
#>   15  0.6889439  0.9959249  0.13080808
#>   17  0.6943288  0.9959249  0.11666667
#>   19  0.6974810  0.9962576  0.10757576
#>   21  0.6966771  0.9965902  0.10000000
#>   23  0.6982154  0.9972556  0.09090909
#>   25  0.7005844  0.9977545  0.08686869
#>   27  0.7009869  0.9974219  0.08030303
#>   29  0.6999713  0.9975882  0.07070707
#>   31  0.7008243  0.9979209  0.06767677
#>   33  0.7015388  0.9981704  0.05656566
#>   35  0.7018798  0.9980041  0.05151515
#>   37  0.7026704  0.9984199  0.05050505
#>   39  0.7024471  0.9985030  0.04393939
#>   41  0.7016133  0.9986693  0.03838384
#>   43  0.7008964  0.9989189  0.03434343
#> 
#> ROC was used to select the optimal model using the largest value.
#> The final value used for the model was k = 37.

12.9.2 Modelo lineal generalizado - GLM

El modelo lineal generalizado (GLM) es una generalización flexible de la regresión lineal ordinaria que permite variables de respuesta que tienen modelos de distribución de errores distintos de una distribución normal. El GLM generaliza la regresión lineal al permitir que el modelo lineal esté relacionado con la variable de respuesta a través de una función de enlace y al permitir que la magnitud de la varianza de cada medición sea una función de su valor predicho.

Para ello necesitamos instalar la librería glmnet antes de crear nuestro modelo.

install.packages("glmnet")
library(glmnet)

churn_modelo_glm <- train(de_baja ~ .,
                   churn_entrena,
                   metric = "ROC",
                   method = "glmnet",
                   trControl = churn_ctrl)
churn_modelo_glm
#> glmnet 
#> 
#> 3501 samples
#>   19 predictor
#>    2 classes: 'No', 'Sí' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (5 reps) 
#> Summary of sample sizes: 701, 700, 700, 700, 700 
#> Resampling results across tuning parameters:
#> 
#>   alpha  lambda        ROC        Sens       Spec      
#>   0.10   0.0001762239  0.7427113  0.9469393  0.28838384
#>   0.10   0.0017622392  0.7598271  0.9504323  0.27323232
#>   0.10   0.0176223919  0.7847811  0.9696435  0.19040404
#>   0.55   0.0001762239  0.7445318  0.9475214  0.28787879
#>   0.55   0.0017622392  0.7675345  0.9534261  0.26565657
#>   0.55   0.0176223919  0.8078084  0.9824511  0.13282828
#>   1.00   0.0001762239  0.7462263  0.9480205  0.28787879
#>   1.00   0.0017622392  0.7739245  0.9557546  0.25707071
#>   1.00   0.0176223919  0.8100897  0.9891877  0.08888889
#> 
#> ROC was used to select the optimal model using the largest value.
#> The final values used for the model were alpha = 1 and lambda = 0.01762239.

12.9.3 Modelo de bosque aleatorio o Random Forest

Random Forest es un técnica de aprendizaje automático supervisada basada en árboles de decisión. Usaremos el modelo de bosque aleatorio (RF) y no un árbol de decisión porque un RF es un conjunto de árboles de decisión combinados. Al combinarlos, lo que en realidad está pasando, es que distintos árboles ven distintas porciones de los datos. Ningún árbol ve todos los datos de entrenamiento. Esto hace que cada árbol se entrene con distintas muestras de datos para un mismo problema. De esta forma, al combinar sus resultados, unos errores se compensan con otros y tenemos una predicción que generaliza mejor.

Para ello primero instalaremos la librería ranger y luego crearemos el modelo.

install.packages("ranger")
library(ranger)

churn_modelo_rf <- train(de_baja ~ .,
                  churn_entrena,
                  metric = "ROC",
                  method = "ranger",
                  trControl = churn_ctrl)
churn_modelo_rf
#> Random Forest 
#> 
#> 3501 samples
#>   19 predictor
#>    2 classes: 'No', 'Sí' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (5 reps) 
#> Summary of sample sizes: 701, 700, 700, 700, 700 
#> Resampling results across tuning parameters:
#> 
#>   mtry  splitrule   ROC        Sens       Spec      
#>    2    gini        0.8799397  0.9998336  0.02222222
#>    2    extratrees  0.8407305  1.0000000  0.00000000
#>   35    gini        0.9088837  0.9828678  0.65050505
#>   35    extratrees  0.9081950  0.9885221  0.53787879
#>   69    gini        0.9061447  0.9796243  0.65757576
#>   69    extratrees  0.9079349  0.9841977  0.60858586
#> 
#> Tuning parameter 'min.node.size' was held constant at a value of 1
#> ROC was used to select the optimal model using the largest value.
#> The final values used for the model were mtry = 35, splitrule = gini
#>  and min.node.size = 1.

12.9.4 Modelo de máquina de soporte vectorial - SVM

Las máquinas de soporte vectorial o máquinas de vectores de soporte son un conjunto de algoritmos de aprendizaje supervisado desarrollados por Vladimir Vapnik y su equipo en los laboratorios AT&T. Dado un conjunto de puntos, subconjunto de un conjunto mayor (espacio), en el que cada uno de ellos pertenece a una de dos posibles categorías, un algoritmo basado en SVM construye un modelo capaz de predecir si un punto nuevo (cuya categoría desconocemos) pertenece a una categoría o a la otra.

Para crear este modelo usaremos:

churn_modelo_svm <- train(de_baja ~ .,
                   churn_entrena,
                   metric = "ROC",
                   method = "svmRadial",
                   tuneLength = 10,
                   trControl = churn_ctrl)
churn_modelo_svm
#> Support Vector Machines with Radial Basis Function Kernel 
#> 
#> 3501 samples
#>   19 predictor
#>    2 classes: 'No', 'Sí' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (5 reps) 
#> Summary of sample sizes: 701, 700, 700, 700, 700 
#> Resampling results across tuning parameters:
#> 
#>   C       ROC        Sens       Spec     
#>     0.25  0.8133013  0.9860274  0.1035354
#>     0.50  0.8133131  0.9881058  0.1020202
#>     1.00  0.8133082  0.9797067  0.1459596
#>     2.00  0.8138342  0.9854448  0.1156566
#>     4.00  0.8186346  0.9844472  0.1560606
#>     8.00  0.8187712  0.9822850  0.1858586
#>    16.00  0.8103373  0.9824516  0.1818182
#>    32.00  0.8014889  0.9810373  0.1691919
#>    64.00  0.7974460  0.9747168  0.1984848
#>   128.00  0.7967994  0.9814534  0.1494949
#> 
#> Tuning parameter 'sigma' was held constant at a value of 0.007422193
#> ROC was used to select the optimal model using the largest value.
#> The final values used for the model were sigma = 0.007422193 and C = 8.

12.9.5 Modelo Bayesiano ingenuo - Naive Bayes

Naïve Bayes (NB), Bayesiano ingenuo o el Ingenuo Bayes es uno de los algoritmos más simples, pero potentes, para la clasificación basado en el Teorema de Bayes con una suposición de independencia entre los predictores. Naive Bayes es fácil de construir y particularmente útil para conjuntos de datos muy grandes. El clasificador Naive Bayes asume que el efecto de una característica particular en una clase es independiente de otras características.

Para utilizar este modelo utilizaremos la librería naivebayes.

install.packages("naivebayes")
library(naivebayes)

churn_modelo_nb <- train(de_baja ~ .,
                  churn_entrena,
                  metric = "ROC",
                  method = "naive_bayes",
                  trControl = churn_ctrl)

churn_modelo_nb
#> Naive Bayes 
#> 
#> 3501 samples
#>   19 predictor
#>    2 classes: 'No', 'Sí' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (5 reps) 
#> Summary of sample sizes: 701, 700, 700, 700, 700 
#> Resampling results across tuning parameters:
#> 
#>   usekernel  ROC        Sens        Spec     
#>   FALSE      0.5909390  0.06827533  0.9540404
#>    TRUE      0.6429996  1.00000000  0.0000000
#> 
#> Tuning parameter 'laplace' was held constant at a value of 0
#> Tuning
#>  parameter 'adjust' was held constant at a value of 1
#> ROC was used to select the optimal model using the largest value.
#> The final values used for the model were laplace = 0, usekernel = TRUE
#>  and adjust = 1.

12.9.6 Comparación de modelos

Para comparar los modelos, primero crearemos una lista con todos los modelos que hemos creado.

lista_de_modelos <- list(glmmet = churn_modelo_glm,
                   rf = churn_modelo_rf,
                   knn = churn_modelo_knn,
                   svm = churn_modelo_svm,
                   nb = churn_modelo_nb)

Luego, utilizaremos la función resamples la cual nos preparará la data para analizar y visualizar el conjunto de resultados de remuestreo del conjunto de datos común.

comparacion_modelos <- resamples(lista_de_modelos)

comparacion_modelos
#> 
#> Call:
#> resamples.default(x = lista_de_modelos)
#> 
#> Models: glmmet, rf, knn, svm, nb 
#> Number of resamples: 5 
#> Performance metrics: ROC, Sens, Spec 
#> Time estimates for: everything, final model fit

Finalmente, usaremos la función bwplot() para trazar una serie de diagramas de caja donde los diagramas de caja individuales representan los datos subdivididos por cada modelo de acuerdo a la métrica que señalemos.

bwplot(comparacion_modelos, metric = "ROC")

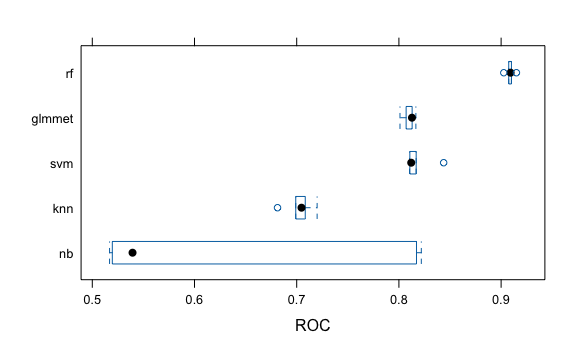
Para este caso el modelo de bosques aleatorios (RF) parece ser el mejor. Esto no es de extrañar dado que este algoritmo estar relacionado con su capacidad para hacer frente a diferentes tipos de entrada y requerir poco preprocesamiento. Podemos hacer nuestros modelos mejor pre procesando datos y cambiando los parámetros ad-hoc de cada modelo.

12.9.7 Prediciendo utilizando el mejor modelo

Ahora que ya tenemos nuestro mejor modelo procedemos a realizar la predicción.

# Este fue nuestro modelo óptimo
modelo_optimo <- churn_modelo_rf

churn_prediccion <- predict(modelo_optimo, churn_test)

confusionMatrix(churn_prediccion, churn_test$de_baja)
#> Confusion Matrix and Statistics
#> 
#>           Reference
#> Prediction   No   Sí
#>         No 1275   49
#>         Sí   12  163
#>                                          
#>                Accuracy : 0.9593         
#>                  95% CI : (0.948, 0.9687)
#>     No Information Rate : 0.8586         
#>     P-Value [Acc > NIR] : < 2.2e-16      
#>                                          
#>                   Kappa : 0.8193         
#>                                          
#>  Mcnemar's Test P-Value : 4.04e-06       
#>                                          
#>             Sensitivity : 0.9907         
#>             Specificity : 0.7689         
#>          Pos Pred Value : 0.9630         
#>          Neg Pred Value : 0.9314         
#>              Prevalence : 0.8586         
#>          Detection Rate : 0.8506         
#>    Detection Prevalence : 0.8833         
#>       Balanced Accuracy : 0.8798         
#>                                          
#>        'Positive' Class : No             
#> 

Así, hemos encontrado cómo crear un modelo de predicción de fuga de clientes dado 19 variables de predicción con una exactitud del 96%.

12.10 Ejercicios

114. El data frame attrition de la librería modeldata muestra los datos de una relación de casi 1,500 trabajadores de una empresa. Crear una copia de este data frame y almacenalo en el objeto trabajadores. Luego, constuir un modelo RF con estos datos para predecir el campo Attrition (deserción laboral). Donde la clase “Yes” quiere decir que renunció y “No” quiere decir que aun trabaja.

Solución

data(attrition)
str(attrition)

trabajadores <- attrition

trabajadores <- trabajadores %>% 
  rename(renuncia = Attrition)

# 70% para la data de entrenamiento
index_entrena <- createDataPartition(y = trabajadores$renuncia, p = 0.7, list = FALSE)

trabajadores_entrena <- trabajadores[index_entrena, ]
trabajadores_test <- trabajadores[-index_entrena, ]

# Creamos folds para potenciales comparaciones futuras
folds_manual <- createFolds(trabajadores_entrena$renuncia, k = 5)

trabajadores_ctrl <- trainControl(
  savePredictions = TRUE,
  classProb = TRUE, 
  summaryFunction = twoClassSummary,
  index = folds_manual
)

# Creamos el modelo
trabajadores_modelo_rf <- train(renuncia ~ .,
                  trabajadores_entrena,
                  metric = "ROC",
                  method = "ranger",
                  trControl = trabajadores_ctrl)

trabajadores_modelo_rf

115. Utilizando la data de entrenamiento del ejercicio anterior, construye el modelo GLM.

Solución

# Creamos el modelo GLM
trabajadores_modelo_glm <- train(renuncia ~ .,
                  trabajadores_entrena,
                  metric = "ROC",
                  method = "glmnet",
                  trControl = trabajadores_ctrl)

trabajadores_modelo_glm

116. Utilizando la data de entrenamiento, construye el modelo SVM.

Solución

# Creamos el modelo SVM
trabajadores_modelo_svm <- train(renuncia ~ .,
                  trabajadores_entrena,
                  metric = "ROC",
                  method = "svmRadial",
                  trControl = trabajadores_ctrl,
                  tuneLength = 10)

trabajadores_modelo_svm

117. A partir de los modelos creados, ¿cuál es el más óptimo?

Solución

# Generamos lista de modelos
lista_de_modelos <- list(rf = trabajadores_modelo_rf,
                         glmmet = trabajadores_modelo_glm,
                         svm = trabajadores_modelo_svm)

# Comparamos los modelos
comparacion_modelos <- resamples(lista_de_modelos)

# Visualizamos la comparación
bwplot(comparacion_modelos, metric = "ROC")

# Obtenemos el resumen de la comparación
summary(comparacion_modelos, metric = "ROC")

Vemos cómo los resultados se superponen, con lo que podríamos optar por los dos que tengan la media más alta de ROC y entre ellos elegir el que nos un menor rango de valores.

118. Crea las matrices de confusión para los tres modelos creados.

Solución

prediccion_rf <- predict(trabajadores_modelo_rf, trabajadores_test)
confusionMatrix(prediccion_rf, trabajadores_test$renuncia)

prediccion_glm <- predict(trabajadores_modelo_glm, trabajadores_test)
confusionMatrix(prediccion_glm, trabajadores_test$renuncia)

prediccion_svm <- predict(trabajadores_modelo_svm, trabajadores_test)
confusionMatrix(prediccion_svm, trabajadores_test$renuncia)

Tener en cuenta que el modelo con el más alto valor de ROC no necesariamente va a tener el más alto accuracy. Por ello la elección del modelo se realizó en un paso previo. El ROC balancea mejor sensitividad con el ratio de falsos positivos.

Referencias

Fawcett, Tom. 2005. An Introduction to ROC Analysis. Elsevier. https://people.inf.elte.hu/kiss/11dwhdm/roc.pdf.

Jorge M. Lobo, Raimundo Real, Alberto Jiménez-Valverde. 2007. AUC: A Misleading Measure of the Performance of Predictive Distribution Models. Ecological Sounding. https://www2.unil.ch/biomapper/Download/Lobo-GloEcoBioGeo-2007.pdf.

---

14. https://topepo.github.io/caret/index.html↩︎