Capítulo 8 Probabilidades continuas
Recordemos que una variable continua es una variable que toma valores a lo largo de un continuo, esto es, en todo un intervalo de valores. Un atributo esencial de una variable continua es que, a diferencia de una variable discreta, nunca puede ser medida con exactitud; el valor observado depende en gran medida de la precisión de los instrumentos de medición. Con una variable continua hay inevitablemente un error de medida. Como ejemplo, la estatura de una persona (1.72m, 1.719m, 1.7186m….). Otro ejemplo, puede ser el tiempo que toma un atleta en recorrer 100 metros planos, ya que este tiempo puede tomar valores como 9,623 segundos; 10,456485 segundos; 12,456412 segundos; es decir, un intervalo de valores.
Por ejemplo, recordemos que en el data frame heights tenemos las estaturas de un grupo de estudiantes de una universidad.
heights %>%
filter(sex == "Male") %>% # Filtramos solo a los hombres
mutate(estatura = height/39.37) %>% # Convertimos a centrímetros
ggplot() +
aes(sex, estatura, color = estatura) +
geom_point(position = position_jitterdodge())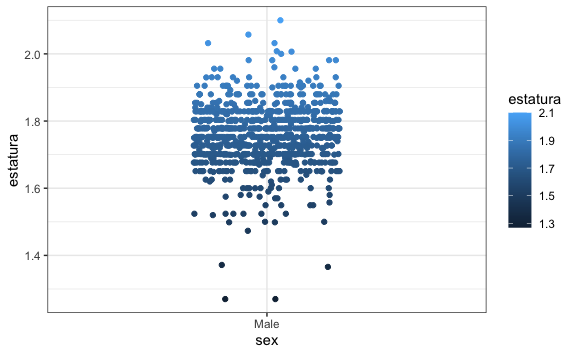
Al graficar la distribución de datos intuitivamente nos damos cuenta que no hace sentido calcular la proporción de personas que miden exactamente 1.73m porque también nos serviría el si una persona mide 1.731, 1.729, o cualquier valor cercano que no es exactamente 1.73 ya se por cómo se midió o cualquier otro tipo de error.
Hace más sentido analizar la data por intervalos, como bien se puede apreciar en este histograma que agrupa por intervalos de 0.05 metros = 5 cm.
heights %>%
filter(sex == "Male") %>% # Filtramos solo a los hombres
mutate(estatura = height/39.37) %>% # Convertimos a centrímetros
ggplot() +
aes(estatura) +
geom_histogram(binwidth = 0.05, color = "black")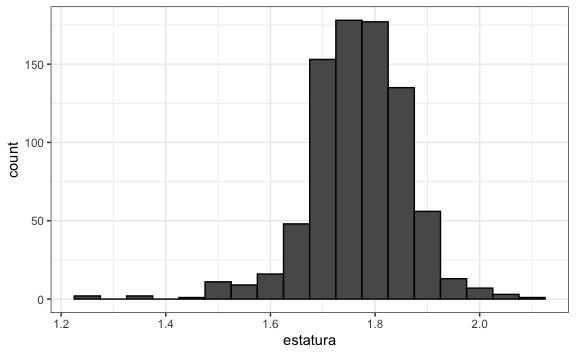
Es mucho más práctico definir una función que opera en intervalos en vez de valores únicos. Para ello utilizamos la función de distribución acumulada (FDA).
8.1 Distribución Empírica
Cuando utilizamos los datos para analizar su distribución hablamos de una distribución empírica. Es la distribución real de un sujeto o una opción, y mide las posibilidades reales e individuales, sobre la medición de la puntuación directa del sujeto, o de una opción de la cual se ha medido la frecuencia de ocurrencia.
Por ejemplo, para nuestro caso podemos crear el vector hombres conformado por todos los valores de la estatura de los hombres:
Luego, podemos crear la función FDA que tome como variable x y nos calcule la proporción de hombres que miden menos o igual a x dentro de los datos encontrados en el vector hombres.
Así, si queremos calcular cuál sería la proporción de estudiantes que miden 1.73m o menos.
Por otro lado, recordemos que la mediana es el valor que divide nuestros datos en dos partes iguales. Con lo que, si calculamos la mediana:
Y luego ingresamos el valor 1.7526035 a nuestra función para preguntar cuál es la proporción de estudiantes que miden 1.7526035 o menos nos debería de salir un valor muy cerca al 50% por definición de la mediana.
Hasta acá hemos calculado proporciones con la función de distribución acumulada FDA. Sin embargo, si queremos saber cuánto es la probabilidad de que al escoger un hombre al azar éste mida 1.9m o menos podríamos utilizar la misma FDA. Dado que cada estudiante tiene las mismas chances de ser elegido la respuesta a la pregunta sería la proporción de estudiantes que miden 1.9 o menos.
\(F(1.9) = P(x \le 1.9)\)
Observamos que la probabilidad es aproximadamente de 93.97%.
Si ahora queremos calcular la probabilidad de que alguien escogido al azar sea más alto que 1.80m primero calculamos la FDA para 1.8 y luego obtenemos el complemento.
\(P(x > 1.8) = 1 - P(x \le 1.8)\)
# Probabilidad de que mida 1.80m o menos
prob <- FDA(1.8)
# Probabilidad de que mida más de 1.80m
1 - prob
#> [1] 0.3583744La probabilidad es aproximadamente 35.8%.
Si ahora quisiéramos saber la probabilidad de que al escoger a alguien al azar éste mida más de 1.6m, pero no más de 1.95m tendríamos.
\(P(x > 1.6\ \cap\ x \le 1.95) = P(x \le 1.95) - P(x \le 1.6)\)
8.2 Distribución Teórica
Por otro lado, se le llama distribución teórica a una distribución que se deriva de ciertos principios o suposiciones por razonamiento lógico y matemático, en oposición a una derivada de datos del mundo real obtenidos por investigación empírica. Entre ellas tenemos la distribución normal, la distribución binomial y la distribución de Poisson.
Por ejemplo, si trazamos una línea aproximada de nuestros datos de estaturas de hombres tendríamos este gráfico:
heights %>%
filter(sex == "Male") %>%
mutate(estatura = height/39.37) %>%
ggplot() +
aes(estatura) +
geom_histogram(binwidth = 0.05, color = "black") +
geom_density(aes(y = ..count..*0.05), colour = "blue", lty = 5)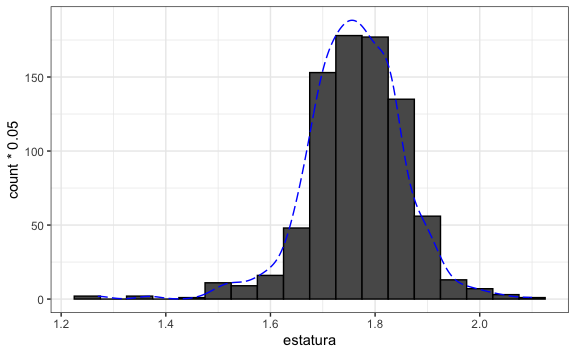
Vemos que la distribución tiene una forma aproximadamente simétrica, de campana. Esta distribución podría modelarse utilizando una distribución normal (también llamada distribución gaussiana, curva de Gauss o campana de Gauss). Para ello, en R utilizaremos la función pnorm(x, promedio, desv_est) para estimar la probabilidad pero utilizando una función de distribución normal con un promedio promedio y una desviación estandar desv_est. De esta forma, podemos estimar cuál es la probabilidad de que si escogemos un valor al azar éste sea menor o igual que x.
Por ejemplo, calculemos nuevamente la probabilidad de que al escoger un hombre al azar éste mida 1.65m o menos, podríamos utilizar la misma FDA y ahora la función pnorm().
# Utilizando la distribución empírica (data real):
FDA(1.9)
#> [1] 0.9396552
# Utilizando la distribución teórica normal (data approx.):
promedio <- mean(hombres)
desv_est <- sd(hombres)
probabilidad <- pnorm(1.9, promedio, desv_est)
probabilidad
#> [1] 0.9357267Obtenemos aproximadamente los mismos resultados. Utilizar una distribución normal nos facilita el trabajo cuando nuestros datos tiene un comportamiento normal.
Matemáticamente estamos calculando el área bajo la curva la cual se ve de color azul:
sec <- seq(-4, 4, length = 100) * desv_est + promedio
normal <- dnorm(sec, promedio, desv_est)
normal %>%
as.data.frame() %>%
rename(valor = ".") %>%
ggplot() +
aes(sec, valor) +
geom_line() +
theme(axis.text.y = element_blank()) +
xlab("Estatura") +
ylab("") +
ggtitle("Distribución normal") +
geom_area(aes(x = ifelse(sec < 1.9, sec, 0)), fill = "blue") +
xlim(min(sec), max(sec)) +
labs(subtitle = paste("P(x <= 1.9) =", probabilidad))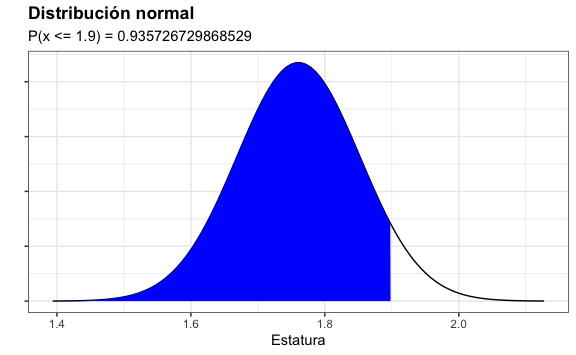
De la misma forma, podríamos estimar la probabilidad de que una persona escogida al azar mida más de 1.8m.
# Utilizando la distribución empírica (data real):
1- FDA(1.8)
#> [1] 0.3583744
# Utilizando la distribución teórica normal (data approx.):
promedio <- mean(hombres)
desv_est <- sd(hombres)
probabilidad <- 1- pnorm(1.8, promedio, desv_est)
probabilidad
#> [1] 0.3337484Matemáticamente estamos calculando el área bajo la curva la cual se ve de color azul:
sec <- seq(-4, 4, length = 100) * desv_est + promedio
normal <- dnorm(sec, promedio, desv_est)
normal %>%
as.data.frame() %>%
rename(valor = ".") %>%
ggplot() +
aes(sec, valor) +
geom_line() +
theme(axis.text.y = element_blank()) +
xlab("Estatura") +
ylab("") +
ggtitle("Distribución normal") +
geom_area(aes(x = ifelse(sec > 1.8, sec, 0)), fill = "blue") +
xlim(min(sec), max(sec)) +
labs(subtitle = paste("P(x > 1.8) =", probabilidad))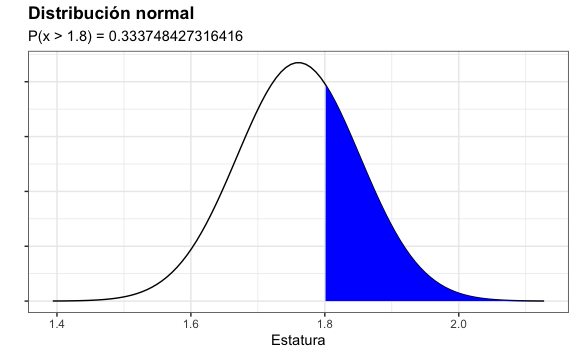
Finalmente, volvamos a calcular la probabilidad de que al escoger a alguien al azar éste mida más de 1.6m, pero no más de 1.95m tendríamos.
# Utilizando la distribución empírica (data real):
prob_1 <- FDA(1.95)
prob_2 <- FDA(1.6)
prob_1 - prob_2
#> [1] 0.9445813
# Utilizando la distribución teórica normal (data approx.):
promedio <- mean(hombres)
desv_est <- sd(hombres)
probabilidad <- pnorm(1.95, promedio, desv_est) - pnorm(1.6, promedio, desv_est)
probabilidad
#> [1] 0.9405618Matemáticamente estamos calculando el área bajo la curva la cual se ve de color azul:
sec <- seq(-4, 4, length = 100) * desv_est + promedio
normal <- dnorm(sec, promedio, desv_est)
normal %>%
as.data.frame() %>%
rename(valor = ".") %>%
ggplot() +
aes(sec, valor) +
geom_line() +
theme(axis.text.y = element_blank()) +
xlab("Estatura") +
ylab("") +
ggtitle("Distribución normal") +
geom_area(aes(x = ifelse(sec > 1.6 & sec <= 1.95, sec, 0)), fill = "blue") +
xlim(min(sec), max(sec)) +
labs(subtitle = paste("P(1.6 < x <= 1.95) =", probabilidad))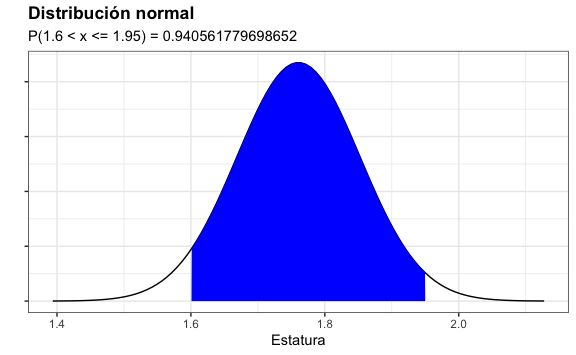
Podemos graficar un diagrama Q-Q, el cual es un diagrama de dispersión creado al trazar dos conjuntos de cuantiles uno contra el otro. La función stat_qq(x) crea un diagrama Q-Q normal. Esta función traza los datos en orden ordenado frente a los cuantiles de una distribución Normal estándar. La función stat_qq_line() agrega una línea de referencia. Si bien entender ello requiere estadística avanzada podemos interpretarlo que si al usar esta función la correlación es muy cercana a la línea entonces nuestra data es muy probable que siga una distribución normal.
heights %>%
filter(sex == "Male") %>%
mutate(estatura = height/39.37) %>%
ggplot() +
aes(sample = estatura) +
stat_qq() +
stat_qq_line()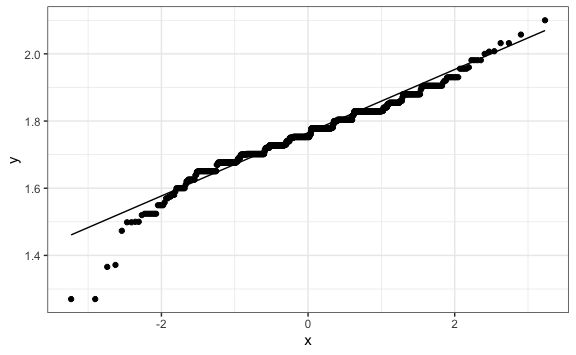
Los puntos parecen caer sobre una línea recta. Esto nos da un buen indicio que suponer que nuestra data de estaturas proviene de una población que es distribuida de forma normal es razonable. Observemos que el el eje-y traza los cuantiles empíricos y eje-x traza los cuantiles teóricos. Éstos últimos son los cuantiles de la distribución Normal estándar con media 0 y desviación estándar 1.
La inspección visual no siempre es confiable. Es posible utilizar una prueba de significación que compare la distribución de la muestra con una normal para determinar si los datos muestran o no una desviación grave de la normalidad. El test más utilizado para estas pruebas es la prueba de normalidad de Shapiro-Wilk.
Para ello usaremos la función shapiro.test(), la cual realiza un test de normalidad y nos arroja un valor de p-value^(https://www.investopedia.com/terms/p/p-value.asp). Se basa en la correlación entre los datos y las puntuaciones normales correspondientes. Si el valor p-value > 0.05 entonces la distribución de los datos no es significativamente diferente de la distribución normal. En otras palabras, podemos asumir la normalidad.
shapiro.test(hombres)
#>
#> Shapiro-Wilk normality test
#>
#> data: hombres
#> W = 0.96374, p-value = 2.623e-13El valor de p-value es menor a 0.05 con lo que, si bien nuestra distribución se asemeja a una normal, no pasa la prueba de significación.
8.3 Ejercicios
Para los siguientes ejercicios supongamos que la distribución de las edades de los estudiantes del curso de Data Science con R se aproxima a una distribución normal con un promedio de 24 años y una desviación estándar de 3. Si seleccionamos a un estudiante al azar:
- ¿Cuál es la probabilidad de que tenga como máximo 23 años?
- ¿Cuál es la probabilidad de que tenga más de 28 años?
- ¿Cuál es la probabilidad de que sea mayor de 22, pero como máximo 27 años?
Solución
- ¿Cuál es la probabilidad de que esté como máximo una desviación estándar alejado del promedio?
8.4 Simulación de Montecarlo para variables continuas
Si bien hemos utilizado una función normal para calcular la probabilidad aproximada, podemos crear más de una función normal con ese promedio y esa desviación estándar. Utilizaremos la función rnorm(n, promedio, desv_est) para crear un vector de n datos aleatorios, de tal forma que estén distribuidos normalmente con un promedio promedio y una desviación estándar desv_est.
Recordemos que nuestra data original tiene las siguientes características:
promedio <- mean(hombres)
promedio
#> [1] 1.760598
desv_est <- sd(hombres)
desv_est
#> [1] 0.09172018
longitud <- length(hombres)
longitud
#> [1] 812Si queremos generar una distribución normal aleatoria usaremos rnorm():
# Creación del vector aleatorio distribuido normalmente:
normal_aleatorio <- rnorm(longitud, promedio, desv_est)
# Creamos un histograma para visualizarlo mejor
hist(normal_aleatorio)
result <- paste("Muestra:", longitud, ". Promedio:",
round(mean(normal_aleatorio), 3), ". Desv. est.:",
round(sd(normal_aleatorio), 3)
)
mtext(result,3)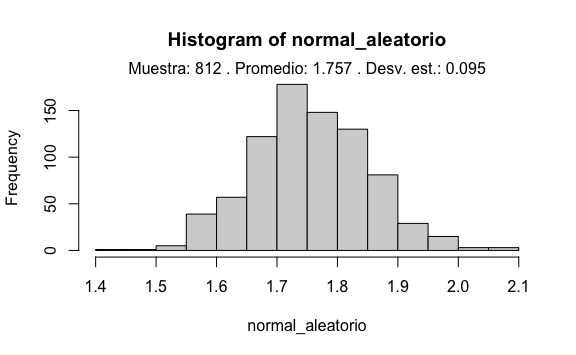
Podemos ejecutar nuevamente el código para verificar que nos genera otra distribución:
# Creación del vector aleatorio distribuido normalmente:
normal_aleatorio <- rnorm(longitud, promedio, desv_est)
# Creamos un histograma para visualizarlo mejor
hist(normal_aleatorio)
result <- paste("Muestra:", longitud, ". Promedio:",
round(mean(normal_aleatorio), 3), ". Desv. est.:",
round(sd(normal_aleatorio), 3)
)
mtext(result,3)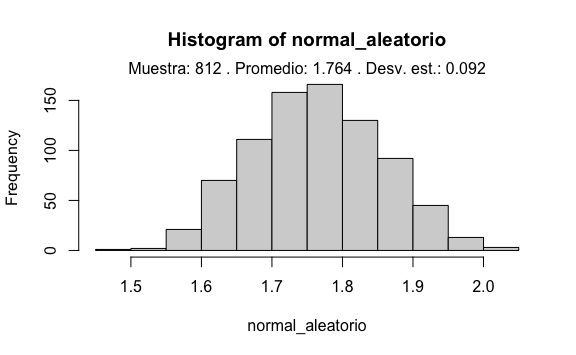
Este experimento de obtener n datos aleatorios que tengan aproximadamente un mismo promedio y una misma desv_est lo podemos repetir unas 10 mil veces para calcular la proporción de veces en que un hombre mide más de 1.8m.
num_veces <- 10000
resultados_simulacion <- replicate(num_veces, {
normal_aleatorio <- rnorm(longitud, promedio, desv_est)
normal_aleatorio > 1.8
})
mean(resultados_simulacion)
#> [1] 0.333873Así, hemos obtenido prácticamente el mismo valor que conseguimos en la sección anterior, pero esta vez estimando utilizando la simulación de Montecarlo.
8.5 Ejercicios
La distribución de las notas del examen de admisión de la Univ. UNISM se distribuye aproximadamente de manera normal. El promedio es 14.5 y la desviación estándar es 1. Queremos saber la distribución del primer puesto. Se sabe que postulan una vez al año 5 mil personas por examen y dan un examen único.
- Generar 5 mil notas unas 1,000 veces usando simulación de Montecarlo y realizar un histograma del resultado.
Solución
- Modifica la simulación anterior para analizar la distribución del promedio de notas de cada año.
Solución
- Usando la primera simulación de Montecarlo creada, calcula la probabilidad de que el primer puesto de notas sea mayor a 18.5.