Capítulo 6 Gapminder
La fundación Gapminder7 es una organización sin fines de lucro con sede en Suecia que promueve el desarrollo global mediante el uso de estadísticas que pueden ayudar a reducir mitos comunes e historias sensasionalistas sobre la salud y la economía mundial. Una selección importante de datos ya está cargada en la librería dslabs en el data frame gapminder. Nuestro caso/problemática ahora será el resolver estas dos preguntas:
- ¿Es razonable aun dividir el mundo entre países occidentales* y países en desarrollo?
- ¿Es cierto que cada día estamos peor y los países ricos se hacen más ricos mientras los pobres se hacen más pobres?
(*): Samuel Huntington en 1993 publicó un artículo llamado Choque de Civilizaciones8 donde definió como países occidentales a los ubicados en las regiones de Norteamérica, Europa del norte/sur/oeste y Australia y Nueva Zelanda.
El proceso que vamos a seguir para resolver las preguntas mencionadas será:
- Exploración de datos
- Entendimiento de los datos
- Análisis de datos hasta encontrar los relevantes para las resolver preguntas
- Visualización y resumen
Primero exploremos la estructura del data frame con str():
gapminder %>%
str()
#> 'data.frame': 10545 obs. of 9 variables:
#> $ country : Factor w/ 185 levels "Albania","Algeria",..: 1 2 3 4 5 6 7 8 9 10 ...
#> $ year : int 1960 1960 1960 1960 1960 1960 1960 1960 1960 1960 ...
#> $ infant_mortality: num 115.4 148.2 208 NA 59.9 ...
#> $ life_expectancy : num 62.9 47.5 36 63 65.4 ...
#> $ fertility : num 6.19 7.65 7.32 4.43 3.11 4.55 4.82 3.45 2.7 5.57 ...
#> $ population : num 1636054 11124892 5270844 54681 20619075 ...
#> $ gdp : num NA 1.38e+10 NA NA 1.08e+11 ...
#> $ continent : Factor w/ 5 levels "Africa","Americas",..: 4 1 1 2 2 3 2 5 4 3 ...
#> $ region : Factor w/ 22 levels "Australia and New Zealand",..: 19 11 10 2 15 21 2 1 22 21 ...Tenemos un data frame con más de 10 mil datos y 9 variables.
Ahora echemos un vistazo a los datos con head():
gapminder %>%
head()
#> country year infant_mortality life_expectancy fertility
#> 1 Albania 1960 115.40 62.87 6.19
#> 2 Algeria 1960 148.20 47.50 7.65
#> 3 Angola 1960 208.00 35.98 7.32
#> 4 Antigua and Barbuda 1960 NA 62.97 4.43
#> 5 Argentina 1960 59.87 65.39 3.11
#> 6 Armenia 1960 NA 66.86 4.55
#> population gdp continent region
#> 1 1636054 NA Europe Southern Europe
#> 2 11124892 13828152297 Africa Northern Africa
#> 3 5270844 NA Africa Middle Africa
#> 4 54681 NA Americas Caribbean
#> 5 20619075 108322326649 Americas South America
#> 6 1867396 NA Asia Western AsiaRecordemos que para data frames de librerías normalmente podemos encontrar la documentación y entender cada atributo más rápido:
Entrar directamente a las preguntas sería no dejar libre esa curiosidad por ver qué hay más allá en la data. Así, vamos a empezar por otras variables como mortalidad infantil, fertilidad o población.
Podemos filtrar todos los datos que sean de Perú y seleccionar la columna país, año, mortalidad infantil y población:
gapminder %>%
filter(country == "Peru") %>%
select(country, year, infant_mortality, population)
#> country year infant_mortality population
#> 1 Peru 1960 135.9 10061519
#> 2 Peru 1961 132.6 10350239
#> 3 Peru 1962 129.1 10650672
#> 4 Peru 1963 125.4 10961539
#> 5 Peru 1964 121.8 11281015
#> 6 Peru 1965 118.2 11607684
#> 7 Peru 1966 114.8 11941327
#> 8 Peru 1967 111.6 12282081
#> 9 Peru 1968 108.7 12629333
#> 10 Peru 1969 106.0 12982444
#> 11 Peru 1970 103.4 13341071
#> 12 Peru 1971 100.9 13704333
#> 13 Peru 1972 98.3 14072476
#> 14 Peru 1973 95.8 14447649
#> 15 Peru 1974 93.3 14832839
#> 16 Peru 1975 91.0 15229951
#> 17 Peru 1976 88.9 15639898
#> 18 Peru 1977 87.0 16061327
#> 19 Peru 1978 85.5 16491087
#> 20 Peru 1979 83.9 16924758
#> 21 Peru 1980 82.4 17359118
#> 22 Peru 1981 80.7 17792551
#> 23 Peru 1982 78.7 18225727
#> 24 Peru 1983 76.3 18660443
#> 25 Peru 1984 73.7 19099575
#> 26 Peru 1985 70.7 19544950
#> 27 Peru 1986 67.6 19996250
#> 28 Peru 1987 64.6 20451712
#> 29 Peru 1988 61.7 20909897
#> 30 Peru 1989 58.9 21368856
#> 31 Peru 1990 56.3 21826658
#> 32 Peru 1991 53.7 22283130
#> 33 Peru 1992 51.0 22737056
#> 34 Peru 1993 48.2 23184222
#> 35 Peru 1994 45.4 23619358
#> 36 Peru 1995 42.5 24038761
#> 37 Peru 1996 39.7 24441076
#> 38 Peru 1997 36.9 24827409
#> 39 Peru 1998 34.3 25199744
#> 40 Peru 1999 31.8 25561297
#> 41 Peru 2000 29.6 25914875
#> 42 Peru 2001 27.6 26261363
#> 43 Peru 2002 25.7 26601463
#> 44 Peru 2003 24.1 26937737
#> 45 Peru 2004 22.6 27273188
#> 46 Peru 2005 21.3 27610406
#> 47 Peru 2006 20.1 27949958
#> 48 Peru 2007 19.0 28292768
#> 49 Peru 2008 18.0 28642048
#> 50 Peru 2009 17.1 29001563
#> 51 Peru 2010 16.3 29373644
#> 52 Peru 2011 15.6 29759891
#> 53 Peru 2012 14.9 30158768
#> 54 Peru 2013 14.2 30565461
#> 55 Peru 2014 13.6 30973148
#> 56 Peru 2015 13.1 31376670
#> 57 Peru 2016 NA NAAgregemos un filtro para obtener solo los datos del 2015:
gapminder %>%
filter(country == "Peru" & year == 2015) %>%
select(country, year, infant_mortality, population)
#> country year infant_mortality population
#> 1 Peru 2015 13.1 31376670Podemos hacer una comparación entre Perú y Chile si creamos un vector y en vez del operador == utilizamos el operador %in% que permite evaluar que nuestros datos están en ese vector.
vector_paises = c("Peru", "Chile")
gapminder %>%
filter(country %in% vector_paises & year == 2015) %>%
select(country, year, infant_mortality, population)
#> country year infant_mortality population
#> 1 Chile 2015 7.0 17948141
#> 2 Peru 2015 13.1 31376670La mortalidad infantil está medida en número de niños que fallecen por cada 1,000 infantes. Esto quiere decir que ya toma en cuenta la población. En el 2015 Perú tenía una mayor tasa de mortalidad infantil que Chile.
6.1 Ploteos iniciales de gapminder
Sin embargo, si queremos analizar datos globales, el comparar país por país nos tomaría mucho más tiempo. Usemos ggplot para ver si existe relación en nuestros datos.
Creemos un gráfico de dispersión con datos del año 1990 de las variables fertilidad (fertility), que es el número promedio de hijos por mujer, y la variable esperanza de vida (life_expectancy).
gapminder %>%
filter(year == 1990) %>%
ggplot() +
aes(x = fertility, y = life_expectancy) +
geom_point()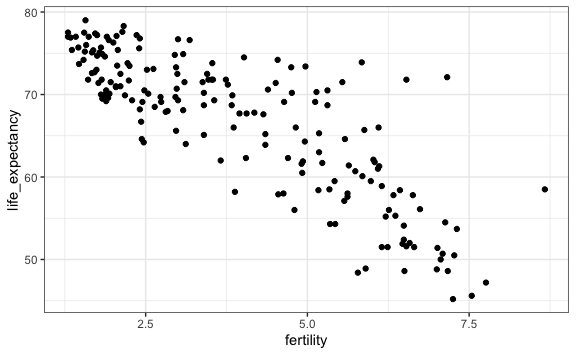
De este gráfico podemos ver que los países donde las familias tienen 7.5 hijos tienen una esperanza de vida menor. Por otro lado, en los países con alta esperanza de vida el promedio de hijos es de menos de 2 hijos por familia.
Como ya lo hemos hecho anteriormente, podemos colorear los puntos de acuerdo a alguna otra variable. En este caso, saber a qué continente pertenecen nos podría dar una mejor idea de la data.
gapminder %>%
filter(year == 1990) %>%
ggplot() +
aes(x = fertility, y = life_expectancy, color = continent) +
geom_point()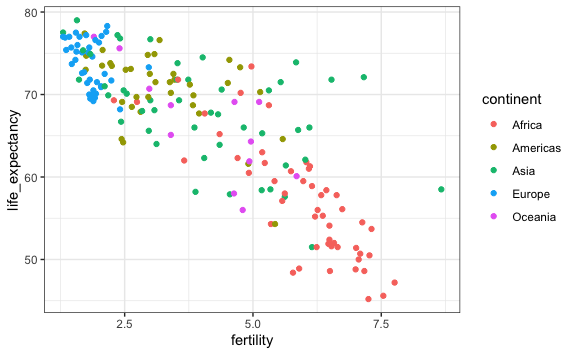
En este gráfico ya se empieza a ver agrupaciones. Varios países Europeos están en el cuadrante superior izquierdo, mientras que varios países de Africa en el cuadrante inferior derecho.
6.2 Facetas
Si bien el gráfico anterior nos muestra ya una correlación de variables, no podemos ver cómo ha cambiado de un año a otro. Para ello usaremos la capa facetas (facet_).
En la capa facet_grid(variable_filas ~ variable_columnas) reemplazamos “variables_filas” por el nombre de nuestra variable o la reemplazamos por un . si es que no queremos alguna de ellas. Por ejemplo, del anterior ejemplo comparemos cómo cambió la distribución comparando el año 1960 con el año 2013.
vector_años <- c(1960, 2013)
gapminder %>%
filter(year %in% vector_años) %>%
ggplot() +
aes(x = fertility, y = life_expectancy, color = continent) +
geom_point() +
facet_grid(year ~ .)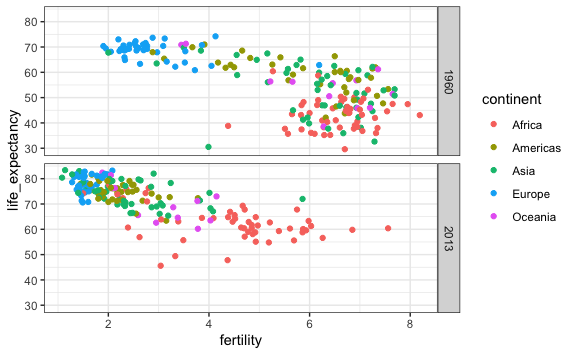
Podemos hacer aun más claro qué continente es el que más cambió si es que agregamos como columna la variable continente.
vector_años <- c(1960, 2013)
gapminder %>%
filter(year %in% vector_años) %>%
ggplot() +
aes(x = fertility, y = life_expectancy, color = continent) +
geom_point() +
facet_grid(year ~ continent)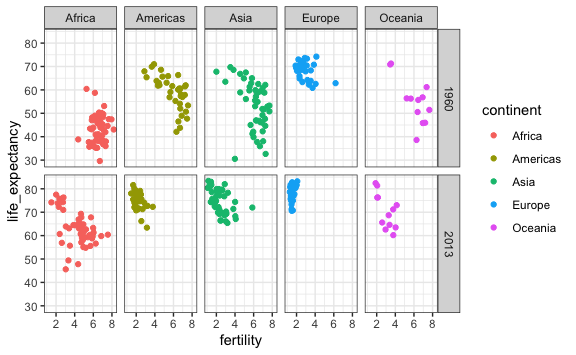
Al haber varias columnas por cada continente se hace más difícil entender porque las columnas se hacen más pequeñas. Es recomendable tener pocas columnas. Entonces invertimos el orden entre año y continente.
vector_años <- c(1960, 2013)
gapminder %>%
filter(year %in% vector_años) %>%
ggplot() +
aes(x = fertility, y = life_expectancy, color = continent) +
geom_point() +
facet_grid(continent ~ year)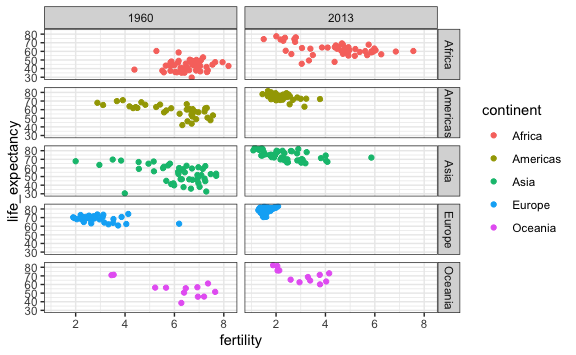
Aquí ya es mucho más evidente el cambio por regiones y como la mayoría de países ha reducido la fertilidad por familia a la vez que ha incrementado la esperanza de vida. Estamos viviendo más que en los 60s y su vez tenemos menos hijos por familia. Esos fenómenos se han dado a nivel global.
No siempre tenemos que mostrar todos las variables, en este caso continentes. Podemos seguir aplicando filtros para que nos muestre un sub conjunto de continentes que queramos comparar. Por ejemplo:
vector_años <- c(1960, 2013)
vector_continents <- c("Europe", "Asia")
gapminder %>%
filter(year %in% vector_años & continent %in% vector_continents) %>%
ggplot() +
aes(x = fertility, y = life_expectancy, color = continent) +
geom_point() +
facet_grid(continent ~ year)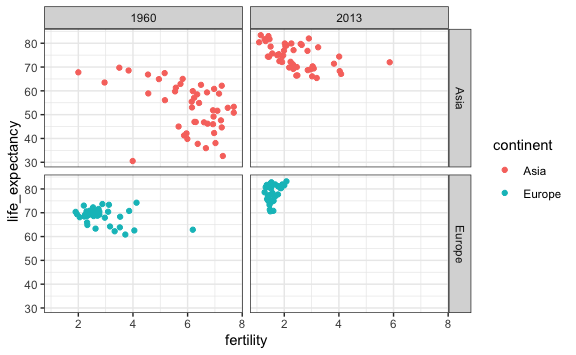
En este caso sería visualmente mejor si los continentes no estuviesen en filas separadas, pero aun se pudiese apreciar en el gráfico. Para ello, usaremos la faceta empaquetar (facet_wrap(~ x)), donde x es la variable que queremos empaquetar. En nuestro caso sería el año, en vez de que aparezca en filas separadas las podemos juntar y transponer.
vector_años <- c(1960, 2013)
vector_continents <- c("Europe", "Asia")
gapminder %>%
filter(year %in% vector_años & continent %in% vector_continents) %>%
ggplot() +
aes(x = fertility, y = life_expectancy, color = continent) +
geom_point() +
facet_wrap( ~ year)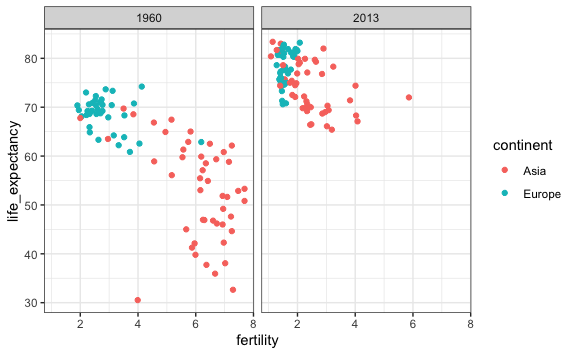
Podemos agregar más datos agregando más datos a los vectores. Por ejemplo, agregemos un corte al medio entre 1960 y 2013.
vector_años <- c(1960, 1985, 2013)
vector_continents <- c("Europe", "Asia")
gapminder %>%
filter(year %in% vector_años & continent %in% vector_continents) %>%
ggplot() +
aes(x = fertility, y = life_expectancy, color = continent) +
geom_point() +
facet_wrap( ~ year)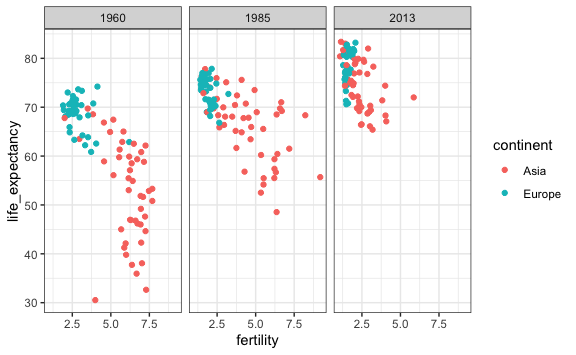
6.3 Series de tiempo
Las series de tiempo son sucesiones de datos medidos en determinados momentos y ordenados cronológicamente. R nos permite fácilmente graficar series de tiempo, solo necesitamos que en nuestros data frames se incluya alguna variable de tiempo.
6.3.1 Series de tiempo individuales
En una serie de tiempo individual solo analizamos cómo ha evolucionado una sola variable, por ejemplo la evolución de la tasa de fertilidad en el Perú. Para esto podemos usar un diagrama de dispersión con puntos o con líneas.
Como recordaremos, usamos geom_point() para puntos:
gapminder %>%
filter(country == "Peru") %>%
ggplot() +
aes(x = year, y = fertility) +
geom_point()
#> Warning: Removed 1 row containing missing values or values outside the scale range
#> (`geom_point()`).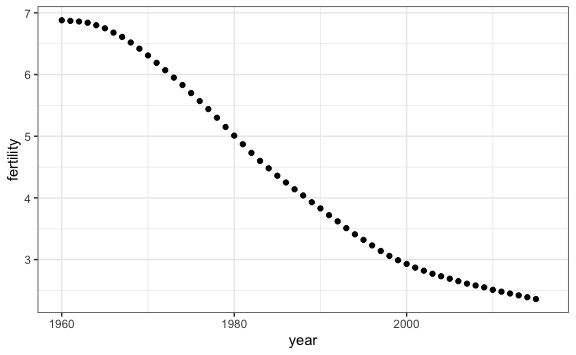
Nos sale un “warning” indicando que hay valores que nos los puede dibujar porque son NA y no están disponibles. Esto no impide mostrar el gráfico.
Si queremos un gráfico de líneas, que es el más usado en series de tiempo, usamos geom_line():
gapminder %>%
filter(country == "Peru") %>%
ggplot() +
aes(x = year, y = fertility) +
geom_line()
#> Warning: Removed 1 row containing missing values or values outside the scale range
#> (`geom_line()`).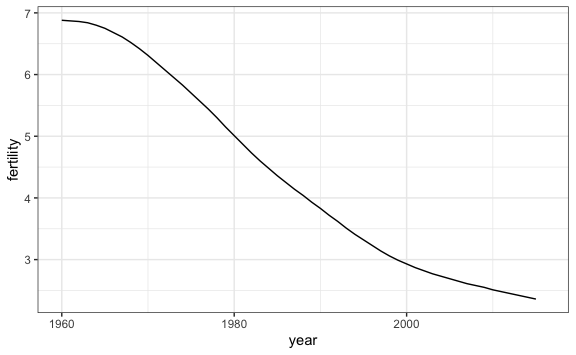
6.3.2 Series de tiempo múltiples
En las series de tiempo múltiples buscamos la comparación para analizar en una serie de tiempo cómo evolucionaron los datos. Por ejemplo, esta sería la serie de tiempo si comparamos Peru, Bolivia y Chile:
paises <- c("Peru", "Bolivia", "Chile")
gapminder %>%
filter(country %in% paises) %>%
ggplot() +
aes(x = year, y = fertility, color = country) +
geom_line()
#> Warning: Removed 3 rows containing missing values or values outside the scale range
#> (`geom_line()`).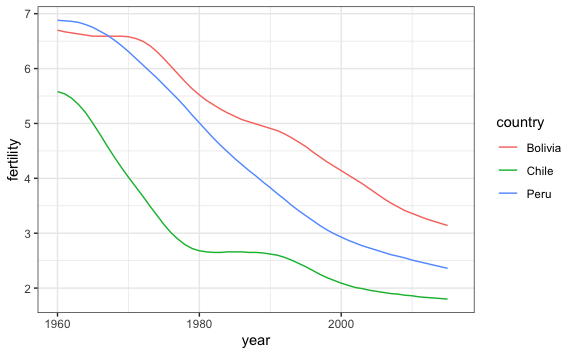
Podemos también agregar quitar la leyenda y mostrar el nombre de los países como etiquetas en el mismo gráfico. Para ello primero tendremos que crear un data frame usando la función data.frame() que nos indique las coordenadas de dónde queremos que salga cada etiqueta:
paises <- c("Peru", "Bolivia", "Chile")
etiquetas <- data.frame(nombre_paises = paises, x = c(1975, 1965, 1962), y = c(6, 7, 4))
etiquetas
#> nombre_paises x y
#> 1 Peru 1975 6
#> 2 Bolivia 1965 7
#> 3 Chile 1962 4Esto lo usaremos para indicar que queremos, por ejemplo, que Bolivia sea escrito en la intersección del año 1972 y con tasa de fertilidad de 6.8.
Para utilizar estas etiquetas en en ggplot editaremos los argumentos en la capa geom_text. Vamos a utilizar los atributos data para indicar que queremos obtener los datos de una fuente externa, e incluiremos la capa aes dentro de geom_text para correlacionar el data frame que hemos creado con el gráfico. Debemos de tener en cuenta que el nombre de la columna en ambos data frame tienen que ser el mismo, en este caso country:
paises <- c("Peru", "Bolivia", "Chile")
etiquetas <- data.frame(country = paises, x = c(1976, 1972, 1965), y = c(5.2, 6.8, 5.5))
gapminder %>% filter(country %in% paises) %>%
ggplot() +
aes(year, fertility, col = country) +
geom_line() +
geom_text(data = etiquetas, aes(x, y, label = country)) +
theme(legend.position = "none")
#> Warning: Removed 3 rows containing missing values or values outside the scale range
#> (`geom_line()`).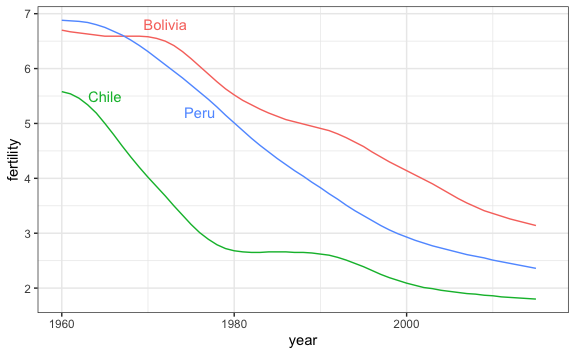
6.4 Ejercicios
Para estos ejercicios seguiremos utilizando el data frame gapminder.
- Crea un diagrama de dispersión de fertilidad versus esperanza de vida del continente Americano en el 2000. Colorea los puntos de acuerdo a la región a la que pertenecen.
Solución
Para crear un vector de secuencias podemos utilizar
X:Y. Ello crear un vector que va desde elnúmero X hasta el número Y
- La guerra de Vietnam ocasionaron muertos tanto en EEUU (United States en inglés) como en Vietnam. Crea un gráfico que permita visualizar cómo cambió la esperanza de vida en cada país. Pista: Filtra estos dos países, así como la población del año 1955 a 1990 y esta serie de tiempo en un gráfico de líneas.
Solución
- Después de la guerra de Vietnam, Pol Pot y Khmer Rouge tomaron el control de Camboya (Cambodia en inglés) desde 1975 a 1979 en una de las dictaduras más sangrientas de la historia. Agrega Camboya al gráfico anterior para visualizar el impacto de este gobierno a la esperanza de vida en ese país.
6.5 Histogramas con ggplot
Podríamos seguir explorando los datos hasta entenderlos mucho mejor. Eventualmente llegaríamos a los datos de PBI (gdp en inglés) y a su vez entenderíamos que comparar únicamente solo PBI no hace sentido puesto que hay países con mucha más población que otros. La transformación de datos no es algo nuevo, pero veremos que es algo recurrente en nuestros análisis.
Vamos a utilizar una transformación que nos permita obtener cuánto es el PBI per cápita por día en cada país en cada año
Podríamos visualizar primero esta variable creando un histograma de la misma. Un histograma en ggplot no es más que una de geoms que tenemos disponibles, en este caso sería geom_histogram(binwidth = x), donde x es el ancho de la barra. Por ejemplo, calculemos la distribución de nuestra variable creada en el año 2010:
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010) %>%
ggplot() +
aes(pbi_per_capita_por_dia) +
geom_histogram(binwidth = 5)
#> Warning: Removed 9 rows containing non-finite outside the scale range
#> (`stat_bin()`).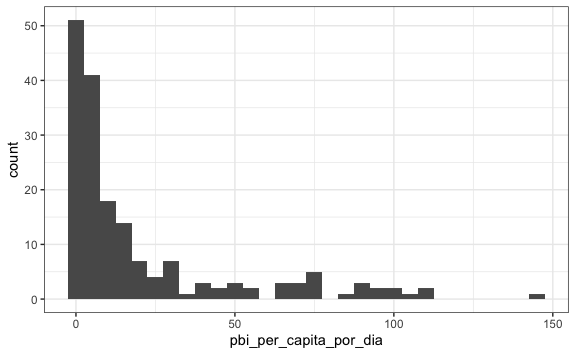
Podemos filtrar los NA para que ya no nos salga low “warnings” con la función que vimos anteriormente is.na(). En este caso como no queremos los NA negaremos la función colocando el símbolo ! al inicio.
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
ggplot() +
aes(pbi_per_capita_por_dia) +
geom_histogram(binwidth = 5)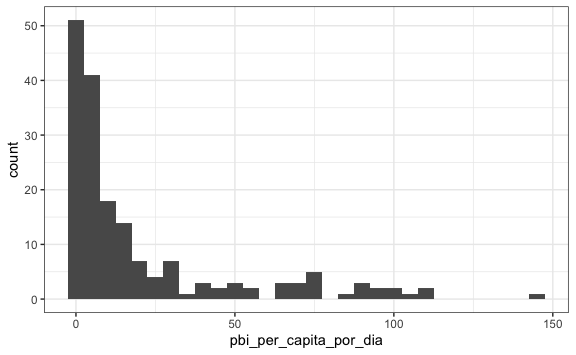
A estas alturas debería de ser rápido detectar que hay una concentración de datos de países con bajo PBI per cápita y podríamos vernos tentados a aplicar una transformación de escala en el eje x. Probemos con logaritmo en base 2:
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
ggplot() +
aes(pbi_per_capita_por_dia) +
geom_histogram(binwidth = 0.5) + #Cambiamos el ancho a 0.5 por la escala logarítmica
scale_x_continuous(trans = "log2")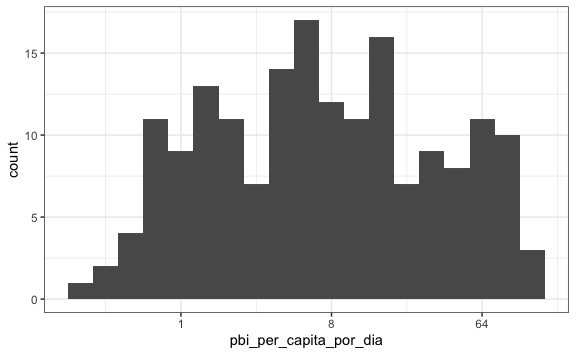
Tengamos cuidado en interpretar este dato. No podemos decir que es una distribución simétrica, aun cuando con esta escala nos vemos tentados a ello. Recordemos la escala y utilicémosla apropiadamente.
6.6 Diagramas de cajas con ggplot
De la misma forma, los diagramas de cajas son un geom más dentro de los disponibles, para ello usaremos la capa geom_boxplot().
Por ejemplo, creemos un gráfico de cajas para analizar por continente el PBI per cápita por día:
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
ggplot() +
aes(continent, pbi_per_capita_por_dia) +
geom_boxplot()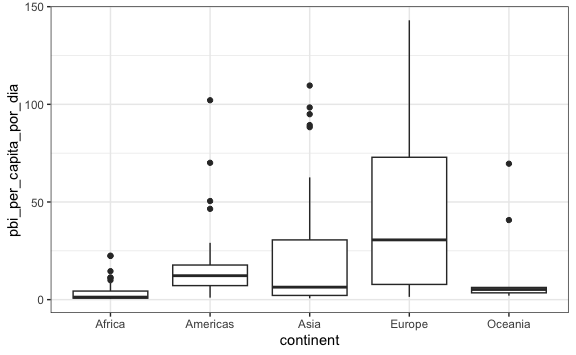
Ahora vayamos a hacer un zoom. Dentro de cada continente tenemos regiones, por ejemplo en las Américas tenemos Sudámerica, Centro América, Norteamética, y así con cada continente. Cambiemos la variable continent por region.
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
ggplot() +
aes(region, pbi_per_capita_por_dia) +
geom_boxplot()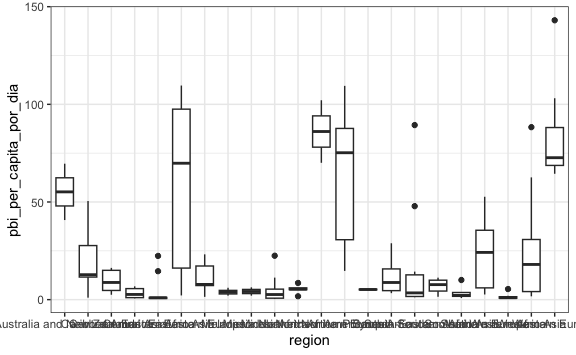
Como podemos comprobar: esta visualización nos permite inferir muy poco. Antes de descartar un gráfico pensemos en si podemos cambiar la configuración para mejorar la visualización.
Lo primero que podemos mejorar es los nombres de las regiones. Están en forma horizontal, pero podríamos rotarlo 45 grados la capa theme().
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
ggplot() +
aes(region, pbi_per_capita_por_dia) +
geom_boxplot() +
theme(axis.text.x = element_text(angle = 45, hjust = 1) )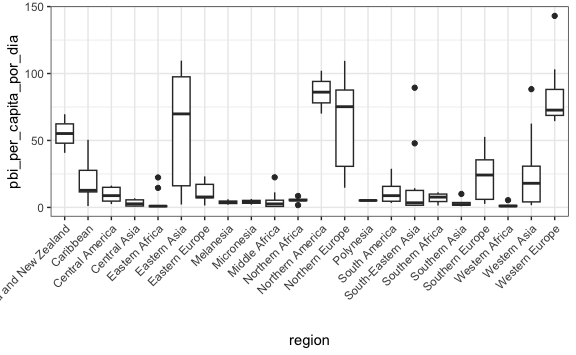
Ya se entienden los nombres, pero si queremos encontrar los top 3 (ya sea por mediana o promedio) tendríamos que buscarlos uno por uno. Vamos a reordenarlo, pero antes seamos conscientes de algunas consideraciones previas:
La columna region es una variable de tipo Factor, no es una cadena de caracteres. Aun cuando visualmente no encontrábamos diferencia, los factores se utilizan para categorizar data. Por ejemplo, clientes bronce, plata, platinum, etc.
Los factores son útiles porque internamente son reemplazados por números y los números, a nivel computacional, son más rápidos de ordenar. El ordenamiento por defecto es alfabético, como podemos apreciar si usamos la función levels.
levels(gapminder$region)
#> [1] "Australia and New Zealand" "Caribbean"
#> [3] "Central America" "Central Asia"
#> [5] "Eastern Africa" "Eastern Asia"
#> [7] "Eastern Europe" "Melanesia"
#> [9] "Micronesia" "Middle Africa"
#> [11] "Northern Africa" "Northern America"
#> [13] "Northern Europe" "Polynesia"
#> [15] "South America" "South-Eastern Asia"
#> [17] "Southern Africa" "Southern Asia"
#> [19] "Southern Europe" "Western Africa"
#> [21] "Western Asia" "Western Europe"Utilizaremos la función reorder() para cambiar el orden de los factores y dado que estamos alterando el dataframe lo tendríamos que usar dentro de la función mutate(). La función reorder() nos pide como primer atributo el factor a reordenar, luego el vector que tomaremos en cuenta y finalmente una función de agrupación. Por ejemplo, que ordene en base a la mediana de cada región (visualmente recordemos que es la línea gruesa dentro de cada caja):
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
mutate(region = reorder(region, pbi_per_capita_por_dia, FUN = median)) %>%
ggplot() +
aes(region, pbi_per_capita_por_dia) +
geom_boxplot() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))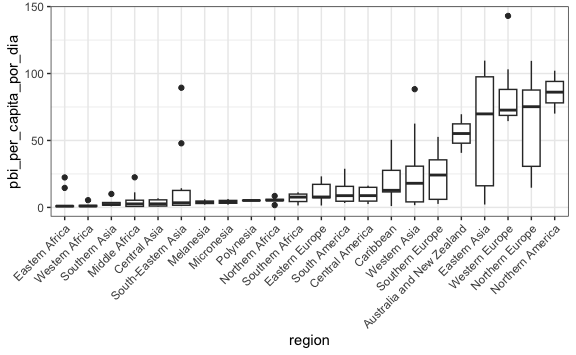
Notemos que se ha colocado un mutate después de filtrar los datos. Esto es para garantizar que estamos removiendo los NA. De otra forma, nos arriesgamos a que todos los valores sean NA y el reordenamiento no se realice y siga siendo por defecto.
Vemos al extremo izquierdo algunas regiones en África, y al extremo derecho Europa y EEUU. Recordemos que podemos agregarle color de acuerdo a a alguna variable. En este caso agreguemos color en base al continente:
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
mutate(region = reorder(region, pbi_per_capita_por_dia, FUN = median)) %>%
ggplot() +
aes(region, pbi_per_capita_por_dia, color = continent) +
geom_boxplot() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))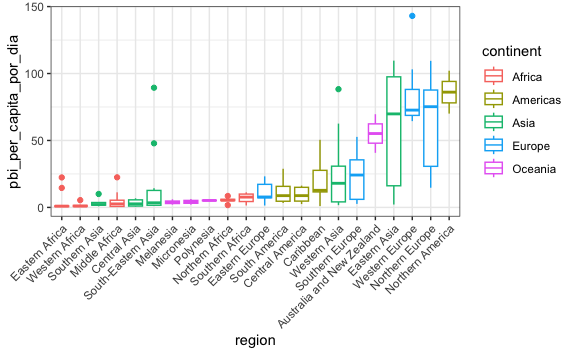
Si bien podemos ya diferenciarlo, en un diagrama de cajas normalmente es el relleno (fill en inglés) de la caja lo que se pinta. Así, cambiemos el atributo color por el atributo fill. Y quitemos la leyenda en el eje-x. No es necesario en este caso en que las regiones se entienden por sí solas.
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
mutate(region = reorder(region, pbi_per_capita_por_dia, FUN = median)) %>%
ggplot() +
aes(region, pbi_per_capita_por_dia, fill = continent) +
geom_boxplot() +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
xlab("")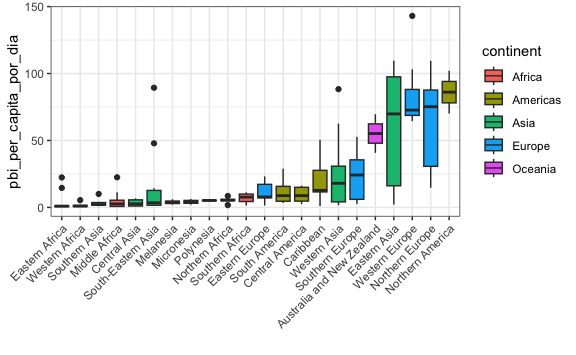
Este gráfico nos ayuda a ver los top 5, pero dado que hay varias regiones concentradas en valores pequeños de PBI per cápita perdemos visualmente esas regiones. Necesitamos una transformación de escala.
Si estás pensando en agregar una capa de escala logarítimica para el eje-y estás por buen camino. Probemos:
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
mutate(region = reorder(region, pbi_per_capita_por_dia, FUN = median)) %>%
ggplot() +
aes(region, pbi_per_capita_por_dia, fill = continent) +
geom_boxplot() +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
xlab("") +
scale_y_continuous(trans = "log2")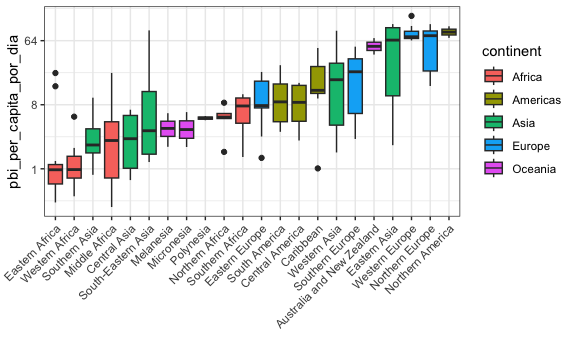
Algunas veces es necesario no solo mostrar las cajas, sino también en dónde se encuentra cada uno de los datos. Para ello podemos agregar la capa geom_point() que ya habíamos usado anteriormente para mostrar los puntos de cada dato.
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
mutate(region = reorder(region, pbi_per_capita_por_dia, FUN = median)) %>%
ggplot() +
aes(region, pbi_per_capita_por_dia, fill = continent) +
geom_boxplot() +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
xlab("") +
scale_y_continuous(trans = "log2") +
geom_point(size = 0.5)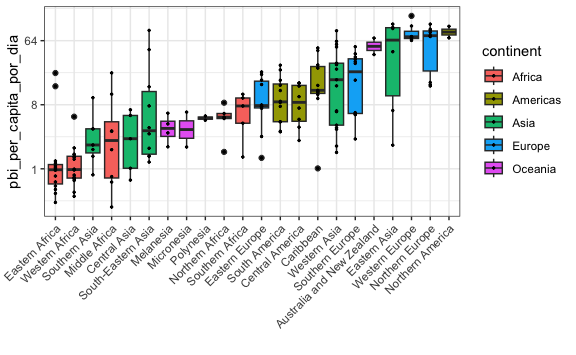
6.7 Comparación de distribuciones
Para poder resolver la primera pregunta del caso tendríamos que comparar las distribuciones de los países de “occidente” versus los países en desarrollo.
Para ello, dado que no tenemos una columna que nos indique cuáles son de occidente, vamos a crear un vector_occidente con el listado de regiones que entran a este categoría:
vector_occidente <- c("Western Europe", "Northern Europe", "Southern Europe", "Northern America", "Australia and New Zealand")Vamos a utilizar también la función
ifelse(test, yes, no)para crear una nueva columna de tal forma que si la región se encuentra en occidente guarde un valor, y si no está en occidente guarde otro valor. Se recomienda leer la documentación en?ifelse.
Agreguemos la columna del grupo al que pertenece cada país:
vector_occidente <- c("Western Europe", "Northern Europe", "Southern Europe", "Northern America", "Australia and New Zealand")
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
mutate(grupo = ifelse(region %in% vector_occidente, "Occidente", "En Desarrollo")) %>%
head()
#> country year infant_mortality life_expectancy fertility
#> 1 Albania 2010 14.8 77.2 1.74
#> 2 Algeria 2010 23.5 76.0 2.82
#> 3 Angola 2010 109.6 57.6 6.22
#> 4 Antigua and Barbuda 2010 7.7 75.8 2.13
#> 5 Argentina 2010 13.0 75.8 2.22
#> 6 Armenia 2010 16.1 73.0 1.55
#> population gdp continent region pbi_per_capita_por_dia
#> 1 2901883 6137563946 Europe Southern Europe 5.794597
#> 2 36036159 79164339611 Africa Northern Africa 6.018638
#> 3 21219954 26125663270 Africa Middle Africa 3.373106
#> 4 87233 836686777 Americas Caribbean 26.277814
#> 5 41222875 434405530244 Americas South America 28.871158
#> 6 2963496 4102285513 Asia Western Asia 3.792527
#> grupo
#> 1 Occidente
#> 2 En Desarrollo
#> 3 En Desarrollo
#> 4 En Desarrollo
#> 5 En Desarrollo
#> 6 En DesarrolloAhora que ya tenemos cómo diferenciar a los países podemos ver su distribución hasta encontrar cómo responder a nuestra pregunta. Empezamos creando un histograma con escala logarítimica en el eje-x y lo separamos usando facet_grid en base al grupo al que pertenece:
vector_occidente <- c("Western Europe", "Northern Europe", "Southern Europe", "Northern America", "Australia and New Zealand")
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year == 2010 & !is.na(pbi_per_capita_por_dia)) %>%
mutate(grupo = ifelse(region %in% vector_occidente, "Occidente", "En Desarrollo")) %>%
ggplot() +
aes(pbi_per_capita_por_dia) +
geom_histogram(binwidth = 1) +
scale_x_continuous(trans = "log2") +
facet_grid(. ~ grupo)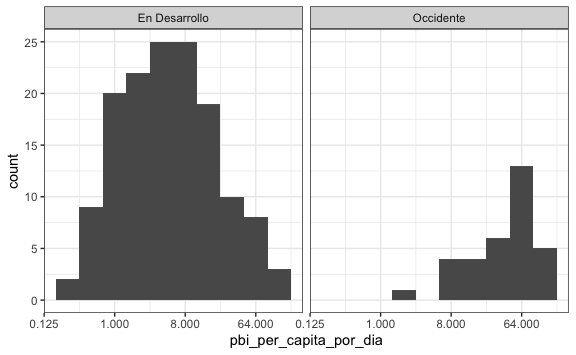
Vemos que el PBI per cápita diario tiene una distribución con valores más altos respecto a los países en desarrollo. Sin embargo, la foto en un año no lo es todo. Ya estamos listos para ver si la separación era la misma 40 años hacia atrás a partir de la fecha que está en el ejemplo (2010). Vamoms a agregar también a la capa geom_histogram() el atributo de color para ver el borde de las barras que por default son plomas.
vector_occidente <- c("Western Europe", "Northern Europe", "Southern Europe", "Northern America", "Australia and New Zealand")
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year %in% c(1970, 2010) & !is.na(pbi_per_capita_por_dia)) %>%
mutate(grupo = ifelse(region %in% vector_occidente, "Occidente", "En Desarrollo")) %>%
ggplot() +
aes(pbi_per_capita_por_dia) +
geom_histogram(binwidth = 1, color = "black") +
scale_x_continuous(trans = "log2") +
facet_grid(year ~ grupo)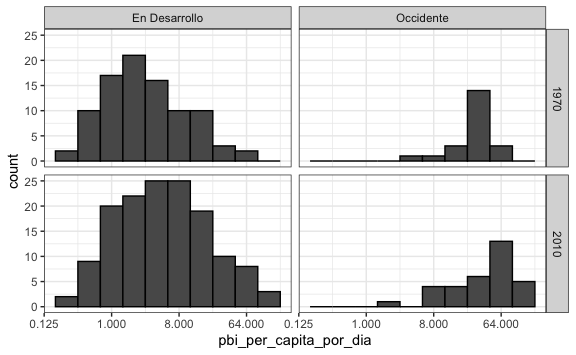
Ambos grupos, tanto los de “Occidente” como los de “En Desarrollo” han mejorado en ese lapso de 40 años, pero los países en desarrollo han avanzado más que los países de occidente.
Hasta acá hemos asumido algo: que todos los países que reportaron en el 2010 también reportaron data en el 1970. Para hacer la comparación más fina tenemos que buscar la distribución de países que tengan datos reportados tanto en 1970 como en el 2010.
Para ello, vamos a crear un vector que liste los países con data en 1970 y otro de los que tienen data en 2010 y luego buscas la intersección. Recordemos que para extraer una columna usamos el operador .$ y luego el nombre de la columna.
vector_occidente <- c("Western Europe", "Northern Europe", "Southern Europe", "Northern America", "Australia and New Zealand")
listado_1 <- gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year %in% c(1970) & !is.na(pbi_per_capita_por_dia)) %>%
.$country
listado_2 <- gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year %in% c(2010) & !is.na(pbi_per_capita_por_dia)) %>%
.$countryPara encontrar la intersección de estos dos vectores utilizaremos la función intersect(vector_1, vector_2), la misma que nos dará el vector que estamos buscando.
Entonces, volvemos a crear nuestro histograma incluyendo solo a los países de esta lista.
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year %in% c(1970, 2010) & !is.na(pbi_per_capita_por_dia)) %>%
filter(country %in% vector_interseccion) %>%
mutate(grupo = ifelse(region %in% vector_occidente, "Occidente", "En Desarrollo")) %>%
ggplot() +
aes(pbi_per_capita_por_dia) +
geom_histogram(binwidth = 1, color = "black") +
scale_x_continuous(trans = "log2") +
facet_grid(year ~ grupo)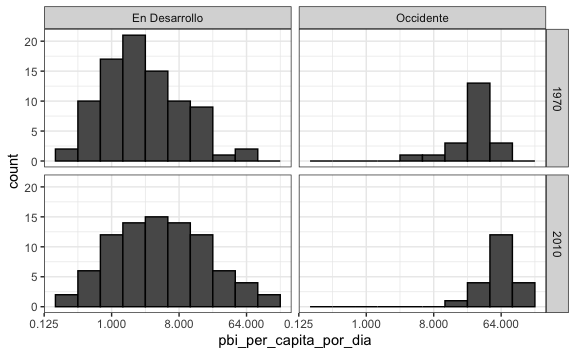
Vemos ahora más claramente con data comparable cómo hay más países dentro de la región en desarrollo que incrementaron el PBI per cápita, mucho más que los países en desarrollo. Pero aun esta primera inferencia es visual, necesitamos comparar cómo cambió la mediana, el rango, etc. Para ello usaremos un diagrama de cajas muy similar al anterior, pero esta vez editaremos geom_boxplot() para que nos muestre en un solo gráfico cómo ha cambiado desde 1970 a 2010 cada región.
gapminder %>%
mutate(pbi_per_capita_por_dia = gdp/population/365) %>%
filter(year %in% c(1970, 2010) & !is.na(pbi_per_capita_por_dia)) %>%
filter(country %in% vector_interseccion) %>%
mutate(region = reorder(region, pbi_per_capita_por_dia, FUN = median)) %>%
ggplot() +
aes(region, pbi_per_capita_por_dia) +
geom_boxplot(aes(region, pbi_per_capita_por_dia, fill=factor(year))) +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
xlab("") +
scale_y_continuous(trans = "log2")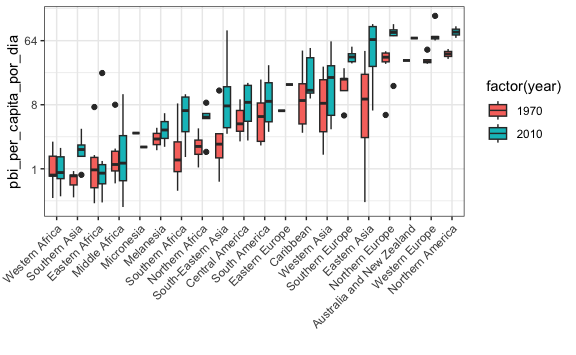
Vemos cómo hay regiones dentro de Asia que han crecido substancialmente. Como sabemos por cultura general, algunos países de Asia son ya potencias, pero hoy con estos gráficos podemos entender bien cuánto ha cambiado hasta convertirse en potencia cada región.
Por lo tanto, ya podemos responder ambas preguntas del caso:
- No es razonable seguir utilizando la categorización de “occidente” y “en desarrollo” puesto que cada vez hay más regiones que están mal representados por esas categorías, como el este de Asia.
- No es cierto que los países ricos se hacen más ricos mientras los pobres se hacer más pobres. Hemos visto que los países en desarrollo tienen incluso un crecimiento mayor que el crecimiento que tienen los países de occidente.
6.8 Ejercicios
Para esta serie de ejercicios usaremos el data frame stars que nos indica atributos de una serie de estrellas como su temperatura, tipo y magnitud.
La columna magnitude es la magnitud absoluta, donde un valor más negativo de una estrella respecto a otra quiere decir que es más luminosa.
Asegúrate de cargar el data frame con data(stars) antes de empezar.
- La temperatura está en grados Kelvin. Agrega la columna temp_celsius usando la siguiente fórmula: C = K - 273.15. Reporta un gráfico de dispersión de temperatura versus magnitud coloreando según el tipo de estrella. Además, cambia la escala del eje-x a logarítmica en base 10.
Solución
- Dado que los valores positivos indican que hay menos brillo, invierte los valores del gráfico anterior usando la capa
scale_y_reverse().
Solución
- El Sol es clasificado como una estrella tipo G. ¿Son las estrellas de tipo G las más luminosas? Crea un gráfico de cajas para comparar medianas de la magnitud y determinar qué tipo de estrellas son las más luminosas.
No, las estrellas de tipo G no son las más luminosas. Para ello podemos elaborar este gráfico:
Texto completo del artículo de Huntington (en inglés)↩︎