11 탐색적 데이터 분석
11.1 들어가기
이 장에서는 데이터를 체계적으로 탐색하기 위해 시각화 및 탐색을 활용하는 과정을 보여준다. 통계학자들은 이 작업을 탐색적 데이터 분석 또는 간단히 EDA (Exploratory Data Analysis)라고 부르며, EDA는 다음과 같은 반복적인 작업으로 이루어져 있다.
데이터에 대한 질문을 만든다.
데이터를 시각화, 변환 및 모델링하여 질문에 대한 답을 찾는다.
질문을 개선하거나 새로운 질문을 만들기 위해 학습한 방법을 사용한다.
EDA 는 엄격한 규칙을 가진 형식적인 과정이 아니다. 무엇보다도 EDA 는 사고하는 상태이다. EDA 의 초기 단계에서는 떠오르는 모든 아이디어를 마음껏 탐색해야 한다. 아이디어 중 일부는 진행될 것이고, 일부는 난관에 부딪힐 것이다. 이러한 탐색을 지속하면 결국에는 스스로 작성한 것 중 사람들과 소통할 수 있는 몇 가지 생산적인 영역으로 집중하게 될 것이다.
질문이 주어진다고 해도 데이터의 품질은 항상 조사해야 하므로 EDA 는 모든 데이터 분석에서 중요한 부분을 차지한다. 데이터 정제는 EDA 의 한 가지 적용일 뿐이며 데이터가 여러분의 기대를 충족하는지 질문한다. 데이터를 정제하기 위해서는 EDA 의 모든 도구(시각화, 변환 및 모델링)를 사용해야 한다.
11.2 질문
“판에 박힌 통계적 질문은 없으며 오직 의심스러운 통계적 질문만이 있다.” — 데이빗 콕스 경 (Sir David Cox)
“꼼꼼하게 만들어진 잘못된 질문에 대해 정확한 대답을 하는 것보다, 모호하지만 올바른 질문에 근사적인 대답을 하는 것이 훨씬 낫다.” — 존 튜키
EDA 의 목표는 데이터를 이해하는 것이다. 이를 위한 가장 쉬운 방법은 탐색을 위한 도구로 질문을 사용하는 것이다. 질문을 하면 데이터셋의 특정 부분에 집중하며 어떤 그래프, 어떤 모델을 만들지 또는 어떤 변환을 할지 결정하는 데 도움을 준다.
EDA 는 근본적으로 창의적인 과정이다. 대부분의 창의적인 과정과 유사하게 우수한 문제를 묻는 것의 핵심은 많은 양의 질문을 생성하는 것이다. 분석의 시작 단계에서는 데이터셋에 어떤 통찰력이 포함되어 있는지 알 수 없기 때문에 흥미로운 질문을 하는 것은 어렵다. 그렇지만 각각의 새로운 질문들은 자신을 데이터의 새로운 측면에 노출시키고 발견할 기회를 증가시킨다. 스스로 발견한 것을 토대로 만든 새로운 질문들을 따라가다 보면, 데이터의 가장 흥미로운 부분을 신속하게 분석하고, 시사하는 바가 큰 질문을 발굴할 수 있다.
탐색을 위해 어떤 질문을 해야 하는가에 대한 규칙은 없다. 그렇지만 데이터 에서 발굴할 수 있는 언제나 유용한 두 가지 유형의 질문이 있으며, 다음과 같은 질문들을 시도해볼 수 있다.
변수 내에서 어떤 유형의 변동이 발생하는가?
변수 간에 어떤 유형의 공변동이 발생하는가?
이 장의 남은 부분에서는 이 두 가지 질문에 대해 살펴볼 것이다. 변동과 공변동에 대해 설명하고 각 질문에 대한 몇 가지 답변을 제시할 것이다. 논의를 쉽게 하기 위해 몇 가지 용어를 정의하고자 한다.
변수(variable)는 측정할 수 있는 양, 질 또는 속성이다.
값(value)은 변수가 측정될 때의 상태이다. 변수의 값은 측정에 따라 변할 수 있다.
관측값(observation)(또는 사례(case))은 유사한 조건에서 측정된 값들의 집합이다 (일반적으로 동시에 같은 대상에 대해 모든 관측된 값을 사용한다.). 관측값은 서로 다른 변수가 조합된 다양한 값을 포함한다. 관측값을 데이터 포인트라고 부르기도 한다.
테이블 형식의 데이터(Tabular data)는 각 변수들과 관측값의 조합인 값들의 집합이다. 테이블 형식의 데이터는 각 값은 ‘셀’에, 변수들은 열에, 관측값은 행에 있을 때 타이디(tidy)하다고 한다. 지금까지 보았던 모든 데이터는 타이디 데이터였다. 실제로 데이터 대부분은 타이디하지 않기 때문에 tidy data에서는 이 부분에 대해 다시 다룰 것이다.
11.3 변량 (variation)
변량(variation) 은 변수의 측정값이 변하는 경향을 말한다. 실생활에서 변량을 쉽게 볼 수 있다. 예를 들어 연속형 변수를 두 번 측정하면 두 개의 다른 결과가 나온다. 이것은 광속과 같은 일정한 양을 측정하더라도 사실이다. 각각의 측정값은 서로 다른 약간의 오차를 포함한다. 범주형 변수도 서로 다른 피실험자(예, 다른 사람들의 눈동자색 차이) 또는 다른 시간(예, 다른 순간의 전자의 에너지 수준)을 측정하는 경우, 다를 수 있다. 모든 변수는 흥미로운 정보를 나타낼 수 있는 고유한 변동 패턴을 가지고 있으며, 이러한 패턴을 이해하는 가장 좋은 방법은 변수들 값의 분포를 시각화하는 것이다.
11.3.1 분포 시각화
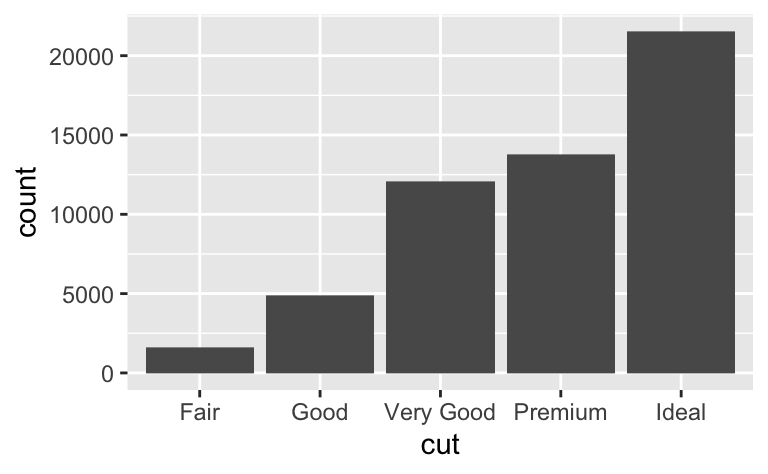
변수의 분포를 시각화하는 방법은 그 변수가 범주형인지 연속형인지에 따라 다르다. 한 변수가 유한개의 집합에서 하나의 값만 가질 수 있다면, 범주형(categorical) 이라고 말한다. R에서 범주형 변수는 일반적으로 팩터형이나 문자형 벡터로 저장된다. 범주형 변수의 분포를 확인하기 위해서는 막대 그래프를 사용한다.
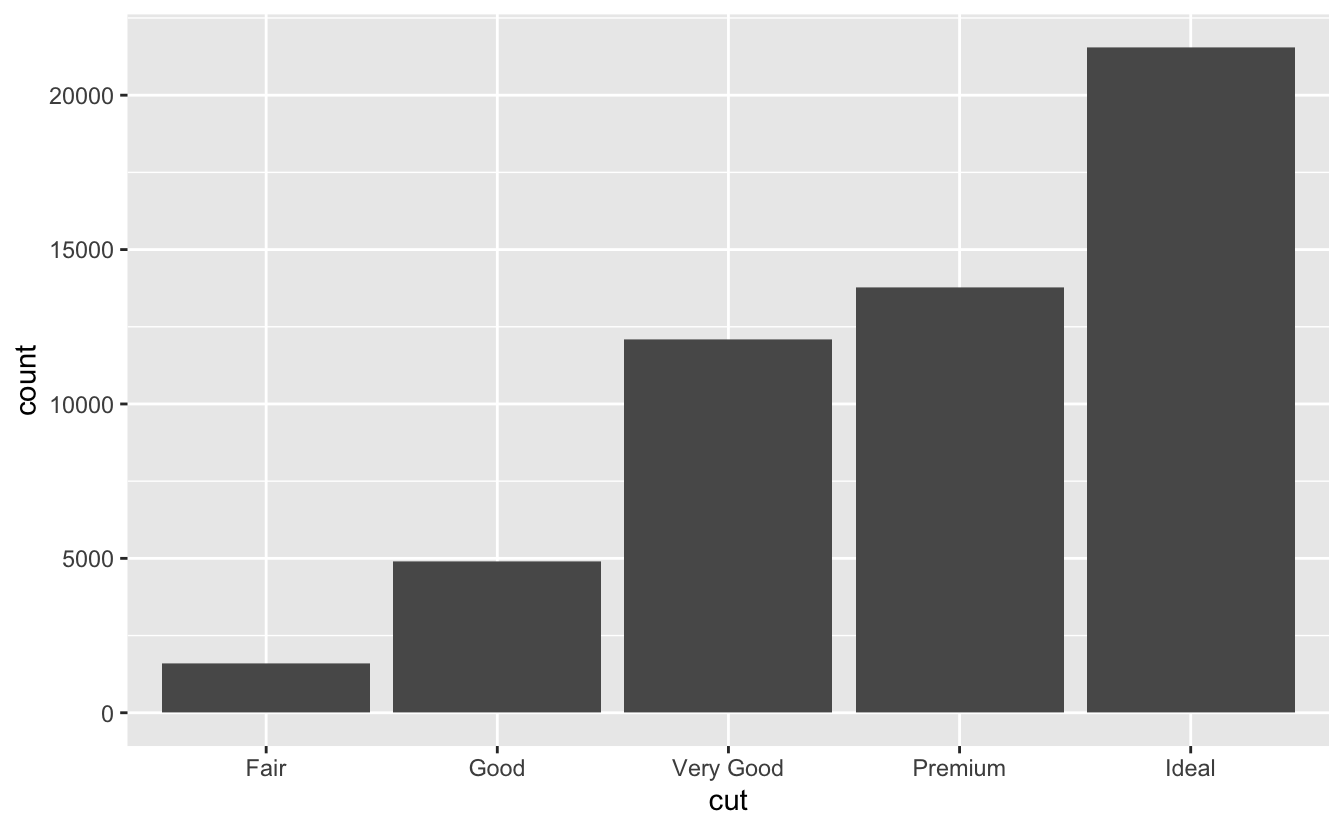
막대의 높이는 각 x값에 대한 관측값의 수를 나타낸다. dplyr::count() 를 사용하여 관측값의 수를 수동으로 계산할 수 있다.
diamonds %>%
count(cut)
#> # A tibble: 5 × 2
#> cut n
#> <ord> <int>
#> 1 Fair 1610
#> 2 Good 4906
#> 3 Very Good 12082
#> 4 Premium 13791
#> 5 Ideal 21551연속형(continuous) 변수는 순서가 있는 무한 집합에서 임의의 값을 가질 수 있는 변수를 말하며, 숫자와 데이트-타임형은 연속형 변수의 예시이다. 연속형 변수의 분포를 확인하기 위해서는 히스토그램을 사용한다.
ggplot(data = diamonds) +
geom_histogram(mapping = aes(x = carat), binwidth = 0.5)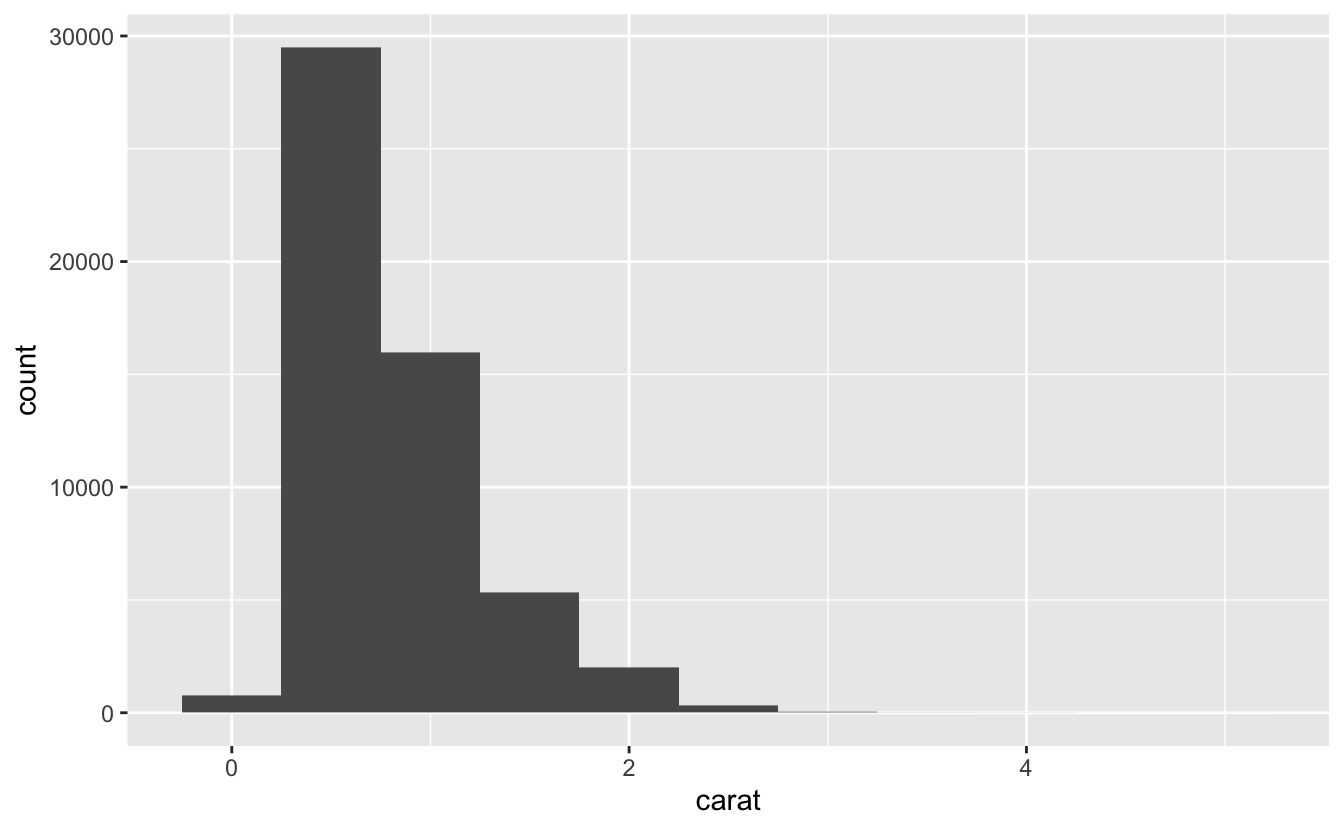
dplyr::count() 와 ggplot2::cut_width() 를 결합하면 값을 직접 계산할 수 있다.
diamonds %>%
count(cut_width(carat, 0.5))
#> # A tibble: 11 × 2
#> `cut_width(carat, 0.5)` n
#> <fct> <int>
#> 1 [-0.25,0.25] 785
#> 2 (0.25,0.75] 29498
#> 3 (0.75,1.25] 15977
#> 4 (1.25,1.75] 5313
#> 5 (1.75,2.25] 2002
#> 6 (2.25,2.75] 322
#> # … with 5 more rows히스토그램은 x축을 동일 간격의 빈(bin)으로 나누고, 각각의 빈에 해당하는 관측값의 수를 표시하기 위해 막대의 높이를 사용한다. 위 그래프에서 가장 긴 막대는 대략 30,000 개의 관측값이 0.25 에서 0.75 사이(가장 긴 막대의 왼쪽 끝에서 오른쪽 끝에 해당)의 carat 값을 가짐을 보여준다.
x 변수의 단위로 측정된 binwidth 인수로 히스토그램 간격의 폭을 설정할 수 있다. 빈 너비에 따라 패턴이 달라질 수 있으므로 히스토그램을 사용하여 작업 할 때는 항상 다양한 빈 너비를 탐색해야 한다. 예를 들어 3캐럿 미만의 다이아몬드로 범위를 줄이고 더 작은 빈 너비를 선택하는 경우, 앞의 그래프가 어떻게 나타나는지 다음의 그래프에서 확인할 수 있다.
smaller <- diamonds %>%
filter(carat < 3)
ggplot(data = smaller, mapping = aes(x = carat)) +
geom_histogram(binwidth = 0.1)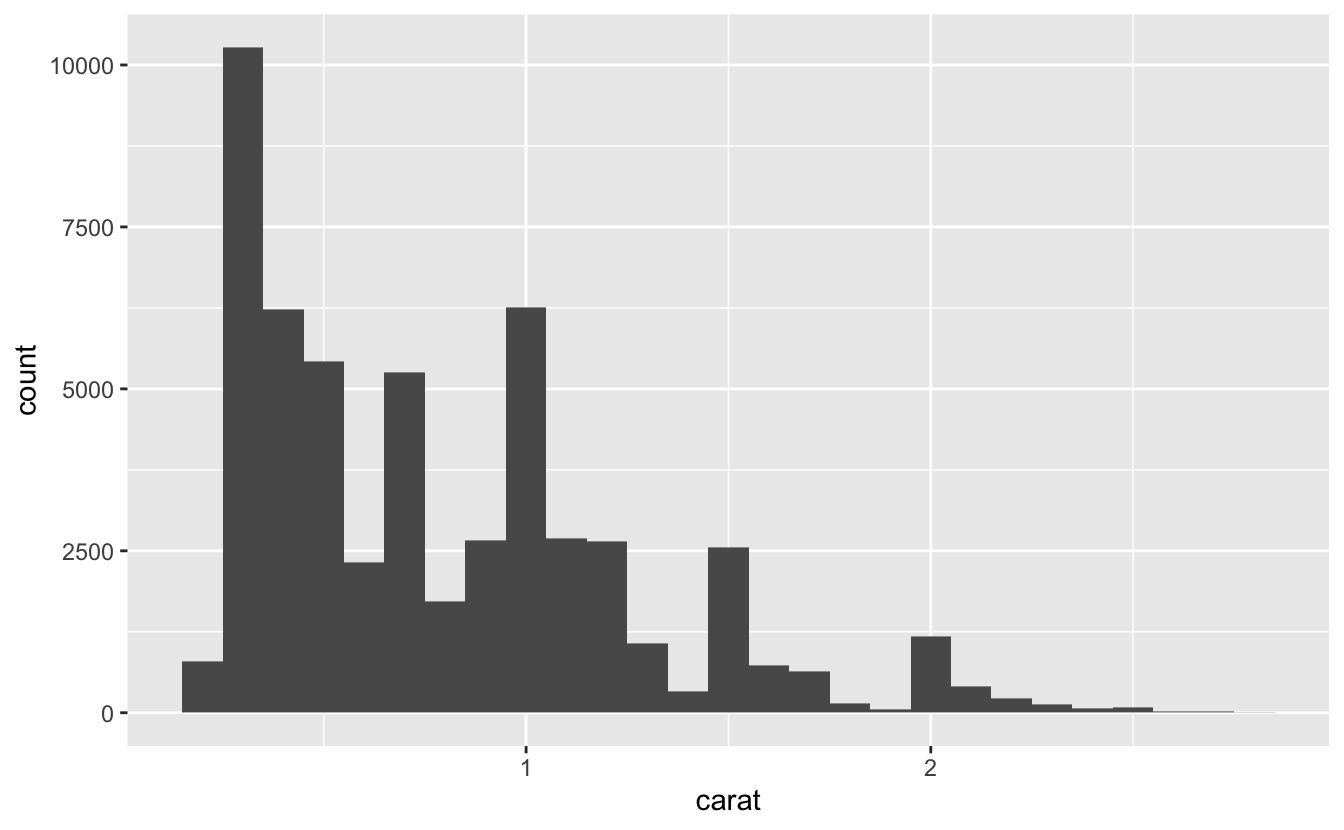
같은 플롯에서 여러 개의 히스토그램을 겹쳐서 그리고 싶다면 geom_histogram() 보다 geom_freqpoly() 를 사용하는 것이 좋다. geom_freqpoly() 는 geom_histogram() 과 연산은 동일하지만 빈도수를 나타내기 위해 막대가 아닌 선을 사용한다. 다음과 같이 막대보다 겹쳐진 선으로 파악하는 것이 훨씬 쉽다.
ggplot(data = smaller, mapping = aes(x = carat, colour = cut)) +
geom_freqpoly(binwidth = 0.1)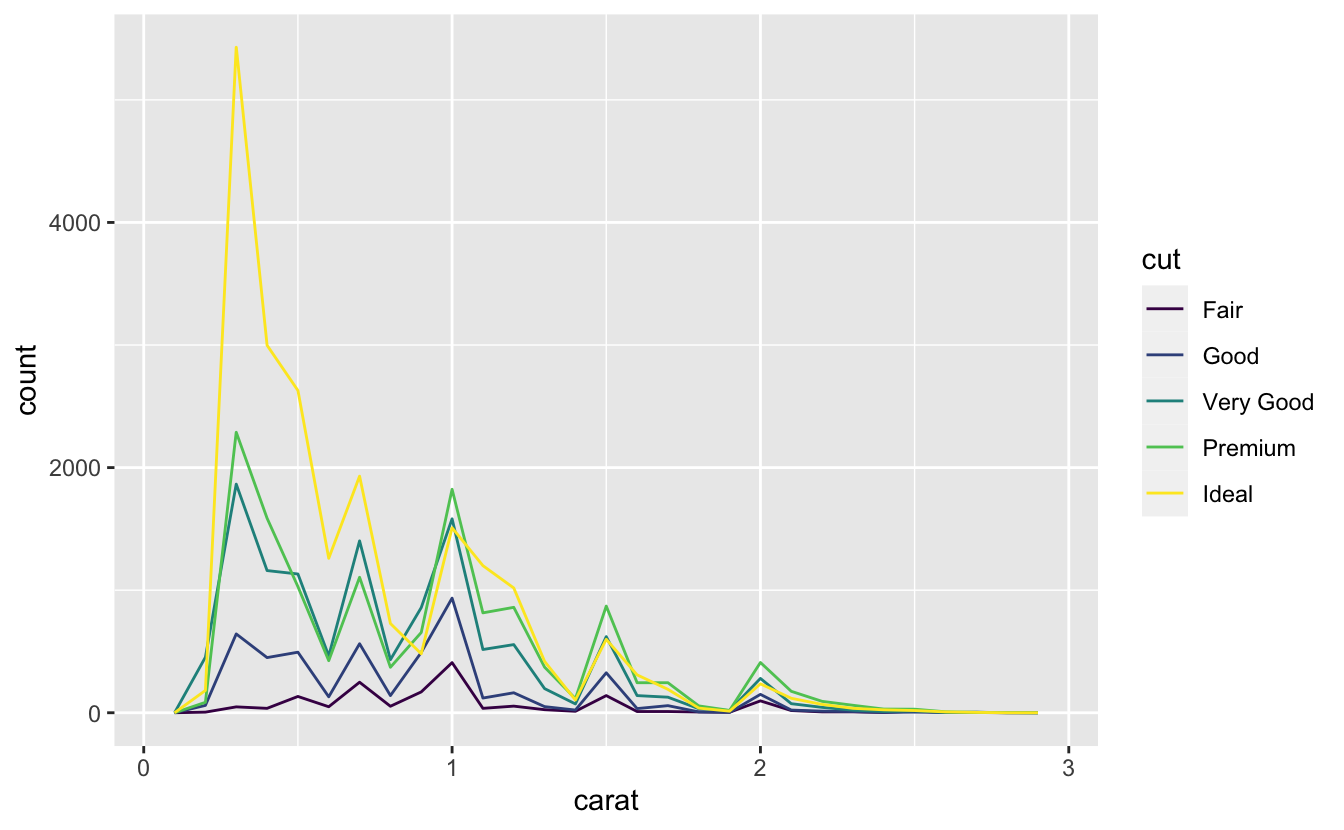
이런 유형의 플롯에는 몇 가지 해결해야 할 과제가 있으므로 visualising a categorical and a continuous variable 에서 다시 살펴볼 것이다.
변량을 시각화했다면, 그래프에서 무엇을 살펴보아야 하나? 어떤 종류의 follow-up 질문을 가져야하나? 아래에 그래프에서 발견할 수 있는 가장 유용한 정보와 각 유형의 정보에 관한 추가 질문들의 리스트를 모아보았다. 좋은 후속 질문을 하는 핵심은 호기심 (무엇을 더 배우고 싶나?) 와 회의적 시각 (이것이 잘못 야기할 것들은 무엇인가?) 을 따르는 것이다.
11.3.2 일반적인 값
막대 그래프와 히스토그램 모두 길이가 긴 막대는 빈도가 높은 값을 나타내고, 짧은 막대는 빈도가 낮은 값을 나타낸다. 막대가 없는 부분은 해당 값의 데이터가 존재하지 않는다는 것을 의미한다. 이런 정보를 유용한 질문으로 전환하기 위해 예상하지 못한 부분을 찾아보자.
어떤 값이 가장 일반적인가? 그 이유는 무엇인가?
드물게 나타나는 값은 무엇인가? 그 이유는 무엇인가? 여러분의 예상과 일치 하는가? 예를 들어 다음의 히스토그램은 몇 가지 흥미로운 질문을 제시한다.
각 피크의 왼쪽보다 오른쪽에 더 많은 다이아몬드가 있는 이유는 무엇인가?
3 캐럿보다 큰 다이아몬드가 없는 이유는 무엇인가?
ggplot(data = smaller, mapping = aes(x = carat)) +
geom_histogram(binwidth = 0.01)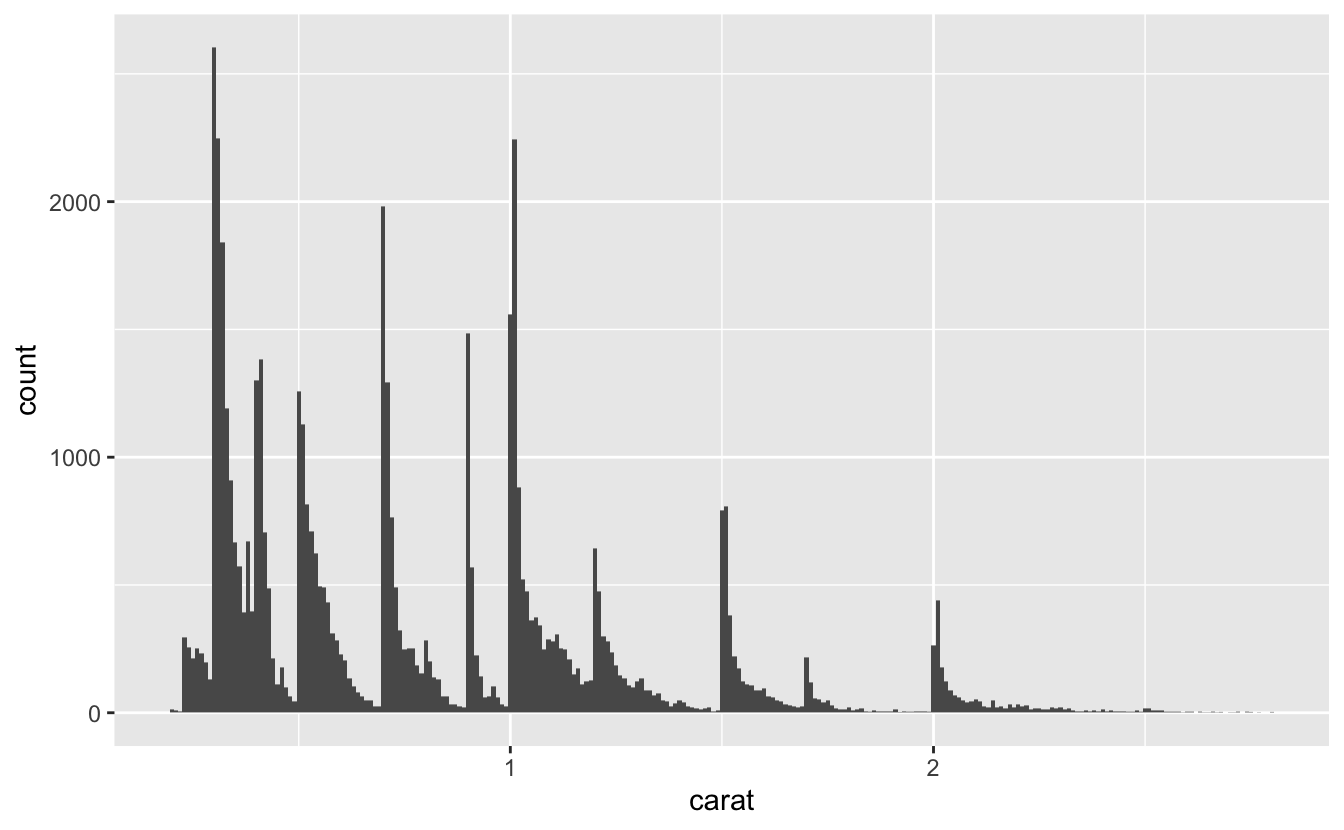
일반적으로 유사한 값들의 군집은 데이터 내에 하위집단이 있다는 것을 의미한다. 하위집단을 이해하기 위하여 다음과 같은 질문을 해보자.
각 군집 내의 관측값은 서로 유사한가?
서로 다른 군집 내의 관측값들은 서로 얼마나 다른가?
군집은 어떻게 설명하거나 묘사할 수 있는가?
군집의 모양이 오해의 소지가 있는 이유는 무엇인가?
아래 히스토그램은 옐로스톤 국립공원의 Old Faithful Geyser(올드 페이스 풀 간헐 온천)에서 발생한 272 번의 화산 분출을 분 단위로 나타낸 것이다. 짧은 분출(약 2분)과 긴 분출(4-5분)이 있고, 그 중간에는 값이 거의 없기 때문에 분출 시간은 2개의 그룹으로 묶인 것처럼 보인다.
ggplot(data = faithful, mapping = aes(x = eruptions)) +
geom_histogram(binwidth = 0.25)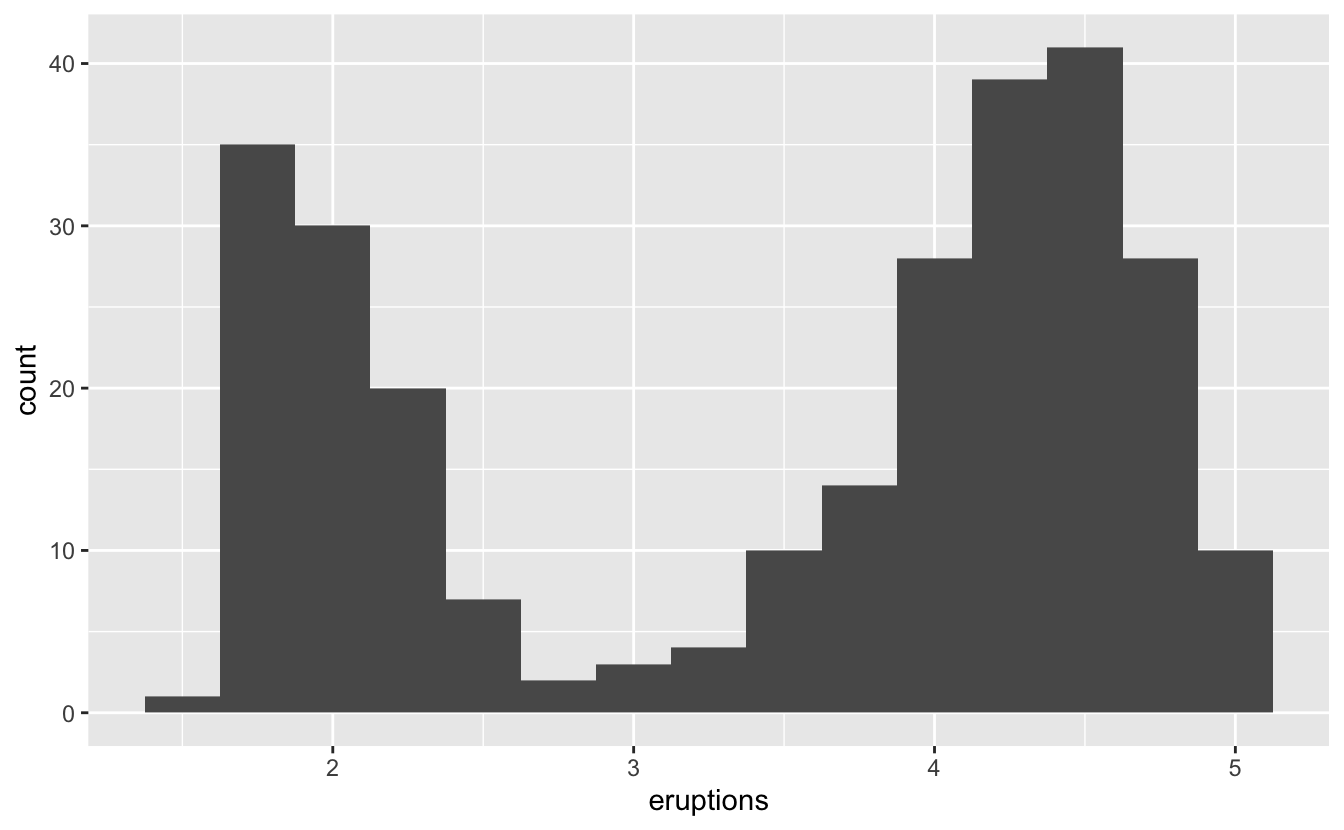
앞의 질문 중 상당수는 한 변수가 다른 변수의 행동을 설명할 수 있는지 확인하기 위해 변수들 간의(between) 관계를 탐색하도록 한다. 이러한 부분은 곧 다루게 될 것이다.
11.3.3 이상값
이상값은 패턴과 맞지 않는 데이터 값으로 비정상적인 관측값을 일컫는다. 때에
따라 이상값은 데이터 입력 오류이거나 중요하면서 새로운 정보를 제시한다. 많은 양의 데이터가 있을 때 히스토그램에서 이상값을 발견하는 것은 어렵다. 예를 들어 다이아몬드 데이터셋에서 y 변수의 분포를 그리는 경우, 이상값의 유일한 단서는 x축의 범위가 매우 넓다는 것이다.
ggplot(diamonds) +
geom_histogram(mapping = aes(x = y), binwidth = 0.5)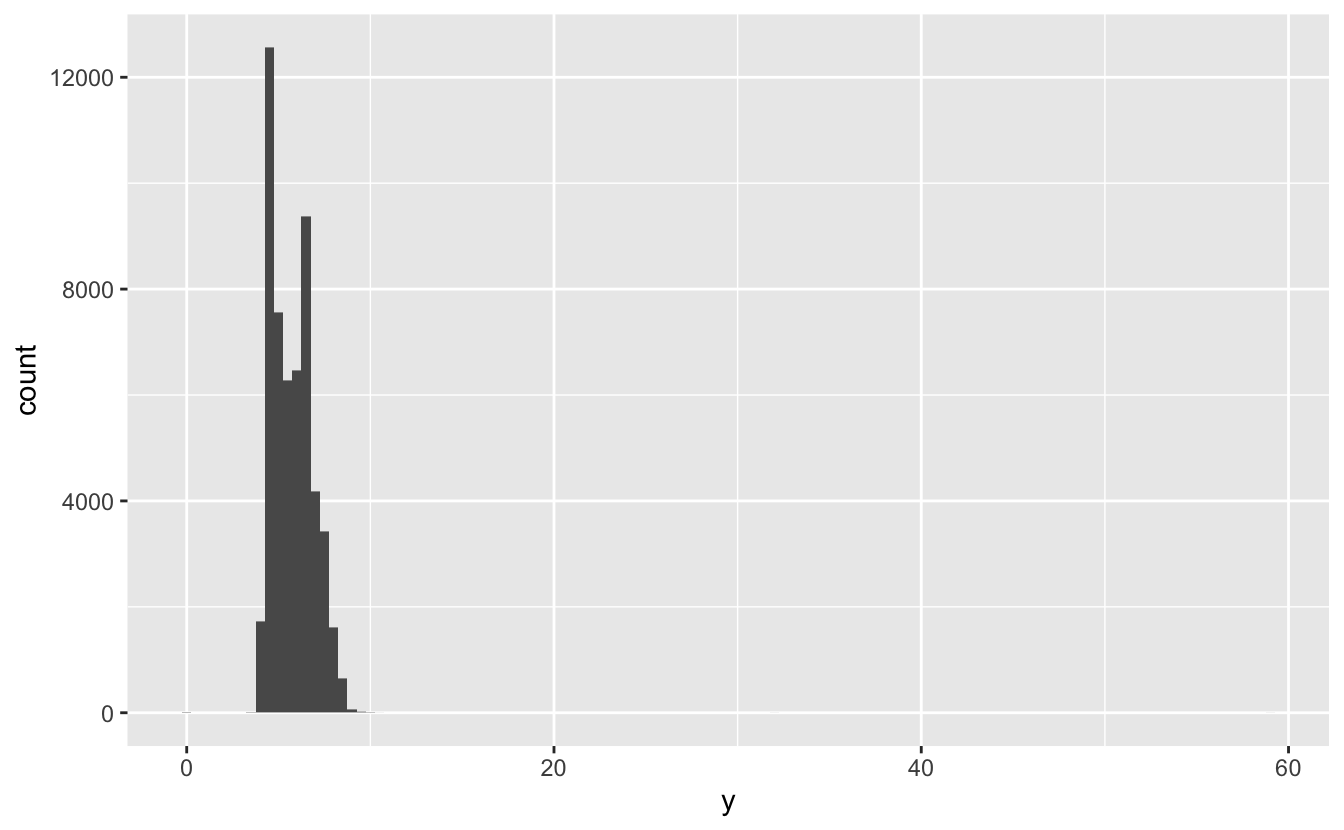
대부분의 빈에는 많은 관측값이 포함되어 있고, 일부 빈은 길이가 너무 짧아 (0
기준선을 골똘히 쳐다보고 무언가를 발견한다 할지라도) 눈으로 확인하기 어렵다. 이상값들을 쉽게 확인하기 위해서는 coord_cartesian() 을 사용하여 y축의 작은 값들을 확대해야 한다.
ggplot(diamonds) +
geom_histogram(mapping = aes(x = y), binwidth = 0.5) +
coord_cartesian(ylim = c(0, 50))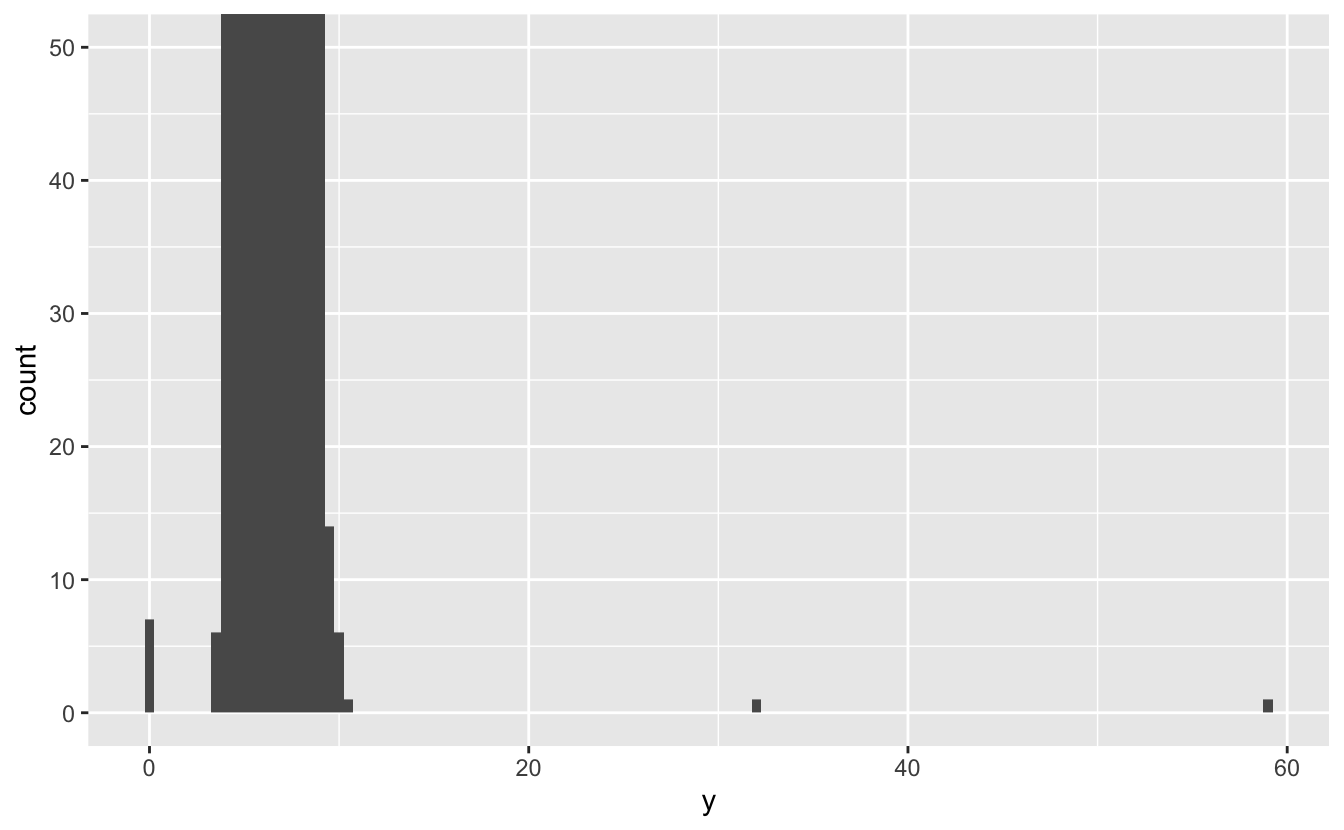
(또, x축을 확대하고자 할 때는 coord_cartesian() 에 xlim() 인수가 있다. ggplot2 에도 약간 다른 기능의 xlim(), ylim() 함수가 있다. 이 함수들은 범위 밖의 데이터들을 제외시킨다.)
이렇게 하면 세 개의 이상값은 0, ~30 및 ~60인 것을 알 수 있다. 이 값들은
dplyr을 사용하여 추출한다.
unusual <- diamonds %>%
filter(y < 3 | y > 20) %>%
select(price, x, y, z) %>%
arrange(y)
unusual
#> # A tibble: 9 × 4
#> price x y z
#> <int> <dbl> <dbl> <dbl>
#> 1 5139 0 0 0
#> 2 6381 0 0 0
#> 3 12800 0 0 0
#> 4 15686 0 0 0
#> 5 18034 0 0 0
#> 6 2130 0 0 0
#> 7 2130 0 0 0
#> 8 2075 5.15 31.8 5.12
#> 9 12210 8.09 58.9 8.06y 변수는 다이아몬드의 3차원 중 하나를 mm 단위로 측정한 값이다. 다이아몬드는 폭이 0mm 가 될 수 없으므로 0mm 값들은 잘못된 값이다. 또 32mm와 59mm
값들도 타당해 보이지 않는다고 추측해볼 수 있다. 이 다이아몬드는 크기가 1인
치 이상이지만 가격은 수십만 달러에 지나지 않는다.
이상값을 포함하거나 제외하여 분석을 반복하는 것은 좋은 연습이다. 이상값이 결과에 최소한의 영향을 미치고 왜 이상값이 발생했는지 그 이유를 알 수 없다면 결측값으로 대체한 후 계속 진행하는 것이 합리적이다. 그러나 이상값이 결과에 상당한 영향을 미치는 경우, 타당한 이유 없이 제외해서는 안 된다. 문제의 원인(예, 데이터 입력 오류)을 파악하고 이상값을 제거한 사실을 밝혀야 한다.
11.3.4 Exercises
Explore the distribution of each of the
x,y, andzvariables indiamonds. What do you learn? Think about a diamond and how you might decide which dimension is the length, width, and depth.Explore the distribution of
price. Do you discover anything unusual or surprising? (Hint: Carefully think about thebinwidthand make sure you try a wide range of values.)How many diamonds are 0.99 carat? How many are 1 carat? What do you think is the cause of the difference?
Compare and contrast
coord_cartesian()vsxlim()orylim()when zooming in on a histogram. What happens if you leavebinwidthunset? What happens if you try and zoom so only half a bar shows?
11.4 결측값
데이터셋에서 이상값을 발견하고 다음 분석으로 넘어가고자 할 때, 다음의 두 가지 옵션이 있다.
-
이상값이 포함된 행 전체를 삭제한다:
하나의 측정값이 유효하지 않다고 해서 모든 측정값이 유효하지 않은 것은 아니므로 이 옵션은 권장하지 않는다. 또한, 저품질의 데이터가 있을 때마다 모든 변수에 대해서 이 방법을 적용하게 된다면 어떤 데이터도 남아있지 않게 될 것이다.
-
대신 이상값을 결측값으로 변경하는 방법을 권장한다. 가장 쉬운 방법으로는
mutate()를 사용하여 변수를 수정된 복사값으로 대체하는 것이다.ifelse()함수를 사용하여 이상값을NA로 바꿀 수 있다:
ifelse() 는 세 개의 인수를 가진다. 첫 번째 인수인 test 는 논리형 벡터이어야 한다. test 값이 TRUE 이면(즉, yes 인 경우) 두 번째 인수가, 거짓이면(즉, no 인 경우) 세 번째 인수가 결과값이 된다. ifelse 가 아닌 다른방법은 dplyr::case_when() 을 사용하는 것이다. case_when() 은 mutate 내부에서 기존 변수들의 복잡한 조합으로 새로운 변수를 생성할때 특히 편리하다.
R 과 동일하게 ggplot2는 결측값이 묵시적으로 사라져서는 안 된다는 방침에 동의한다. 결측값을 어디에 나타낼지 명확하지 않으므로 ggplot2는 결측값을 플 롯에 포함하지는 않지만 결측값이 제거되었음을 경고한다.
ggplot(data = diamonds2, mapping = aes(x = x, y = y)) +
geom_point()
#> Warning: Removed 9 rows containing missing values (geom_point).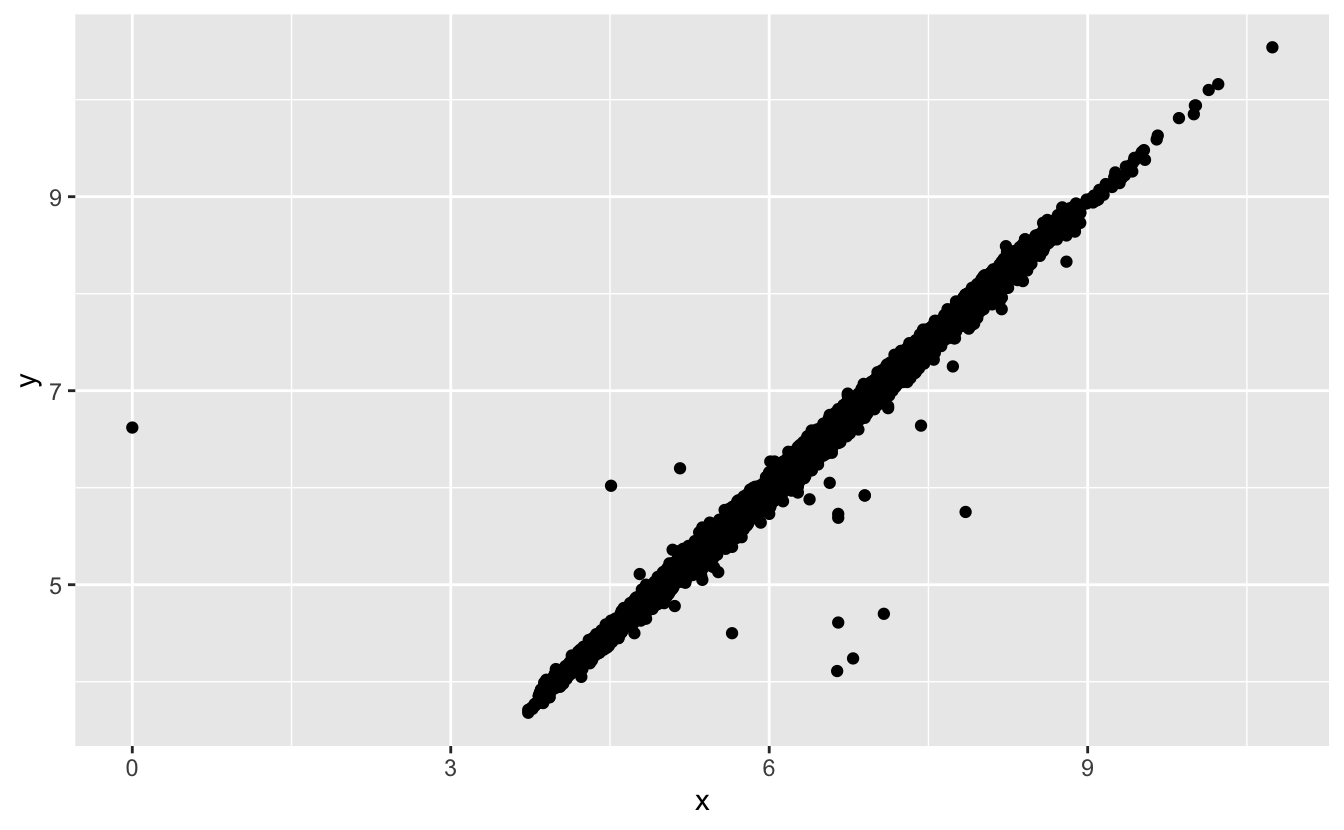
경고 표시를 숨기려면 na.rm = TRUE 로 설정하면 된다.
ggplot(data = diamonds2, mapping = aes(x = x, y = y)) +
geom_point(na.rm = TRUE)때로는 결측값과 기록된 값의 차이를 만드는 것이 무엇인지 알고 싶은 경우가
있다. 예를 들어 nycflights13::flights 에서 dep_time 변수의 결측값은 항공기의
운항이 취소되었다는 것을 나타낸다. 이때 취소된 비행기의 예정 출발 시각과
취소되지 않은 비행기의 출발 시각을 비교하고자 한다. is.na() 를 사용하여 새로운 변수를 생성하면 이를 수행할 수 있다.
nycflights13::flights %>%
mutate(
cancelled = is.na(dep_time),
sched_hour = sched_dep_time %/% 100,
sched_min = sched_dep_time %% 100,
sched_dep_time = sched_hour + sched_min / 60
) %>%
ggplot(mapping = aes(sched_dep_time)) +
geom_freqpoly(mapping = aes(colour = cancelled), binwidth = 1/4)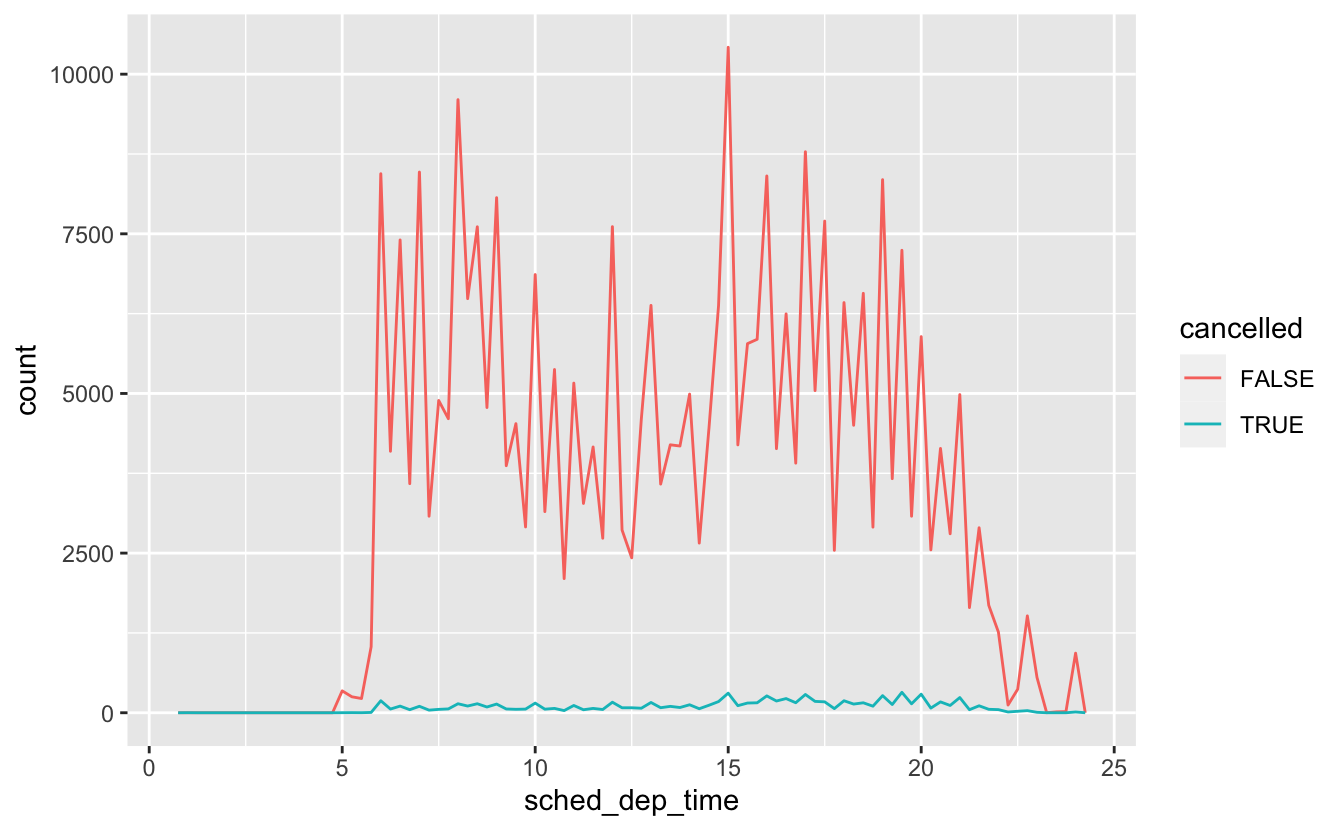
그러나 취소된 항공편보다 취소되지 않은 항공편이 더 많으므로 이 플롯은 유용 하지 않다. 다음 절에서는 이러한 비교를 개선하기 위해 몇 가지 기법을 살펴볼 것이다.
11.5 공변동
변동이 변수 _내_의 움직임을 설명한다면 공변동(covariation)은 변수들 _간_의 움직임을 설명한다. 공변동은 둘 이상의 변숫값이 연관되어 동시에 변하는 경향을 말한다. 공변동을 발견하는 가장 좋은 방법은 두 개 이상의 변수 사이의 관계를 시각화하는 것이다. 시각화하는 방법은 관련된 변수의 유형에 따라 달라진다.
11.5.1 범주형 변수와 연속형 변수
이전의 빈도 다각형과 같이 범주형 변수로 구분된 연속형 변수의 분포를 탐색하고자 하는 것이 일반적이다. geom_freqpoly() 의 기본 모양은 높이가 빈도수를 나타내기 때문에 그러한 종류의 비교에는 유용하지 않다. 즉, 그룹 중 하나가 다른 값들보다 월등히 작으면 형태의 차이를 파악하기 어렵다. 예를 들어 다이아몬드의 가격이 품질에 따라 어떻게 달라지는지 살펴보자.
ggplot(data = diamonds, mapping = aes(x = price)) +
geom_freqpoly(mapping = aes(colour = cut), binwidth = 500)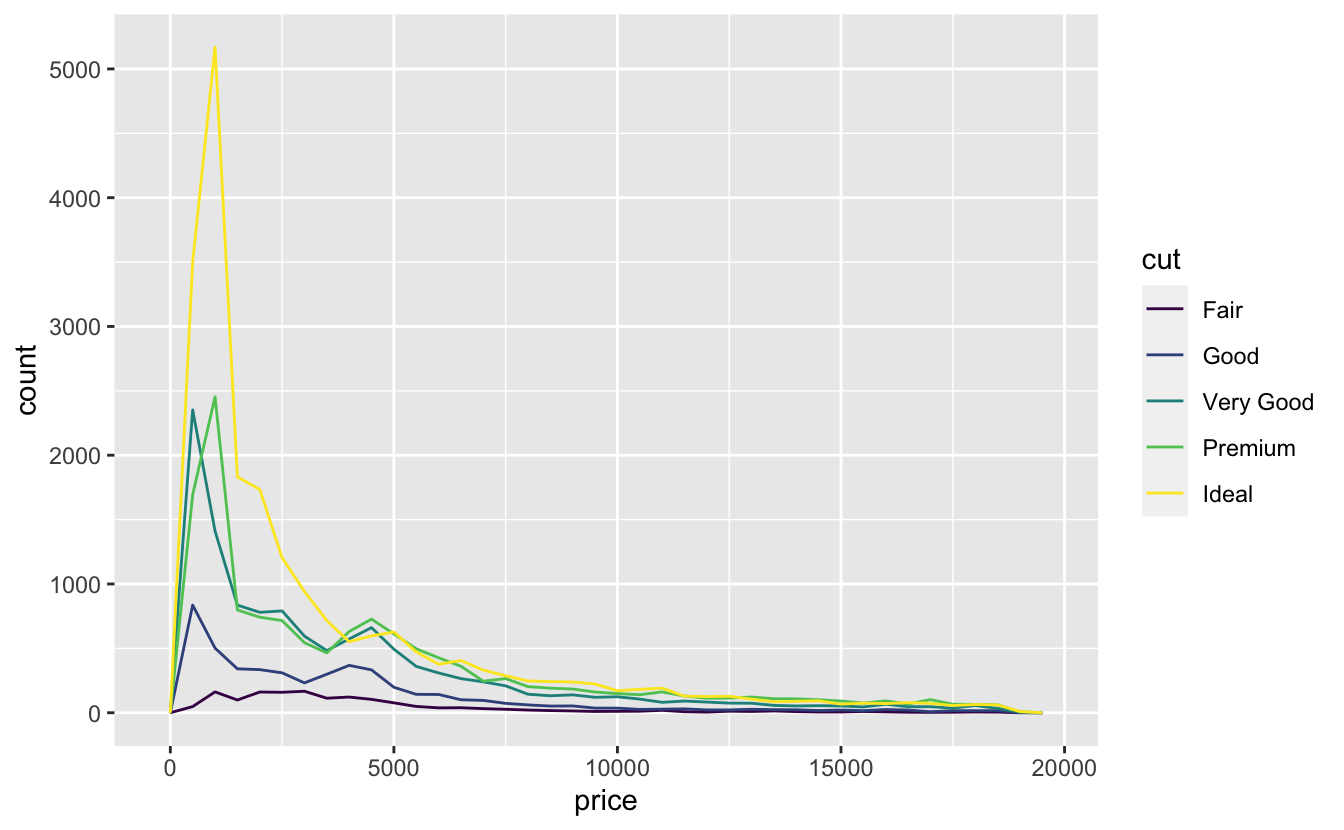
전체적인 빈도수가 많이 다르므로 분포의 차이를 파악하기 어렵다.
비교를 쉽게 하기 위해서 y축에 표시된 내용을 변경할 필요가 있다. 빈도수로 나타내는 대신 빈도 다각형 아래의 영역이 1이 되도록 빈도수를 표준화한 __밀도(density)__로 나타낼 수 있다.
ggplot(data = diamonds, mapping = aes(x = price, y = ..density..)) +
geom_freqpoly(mapping = aes(colour = cut), binwidth = 500)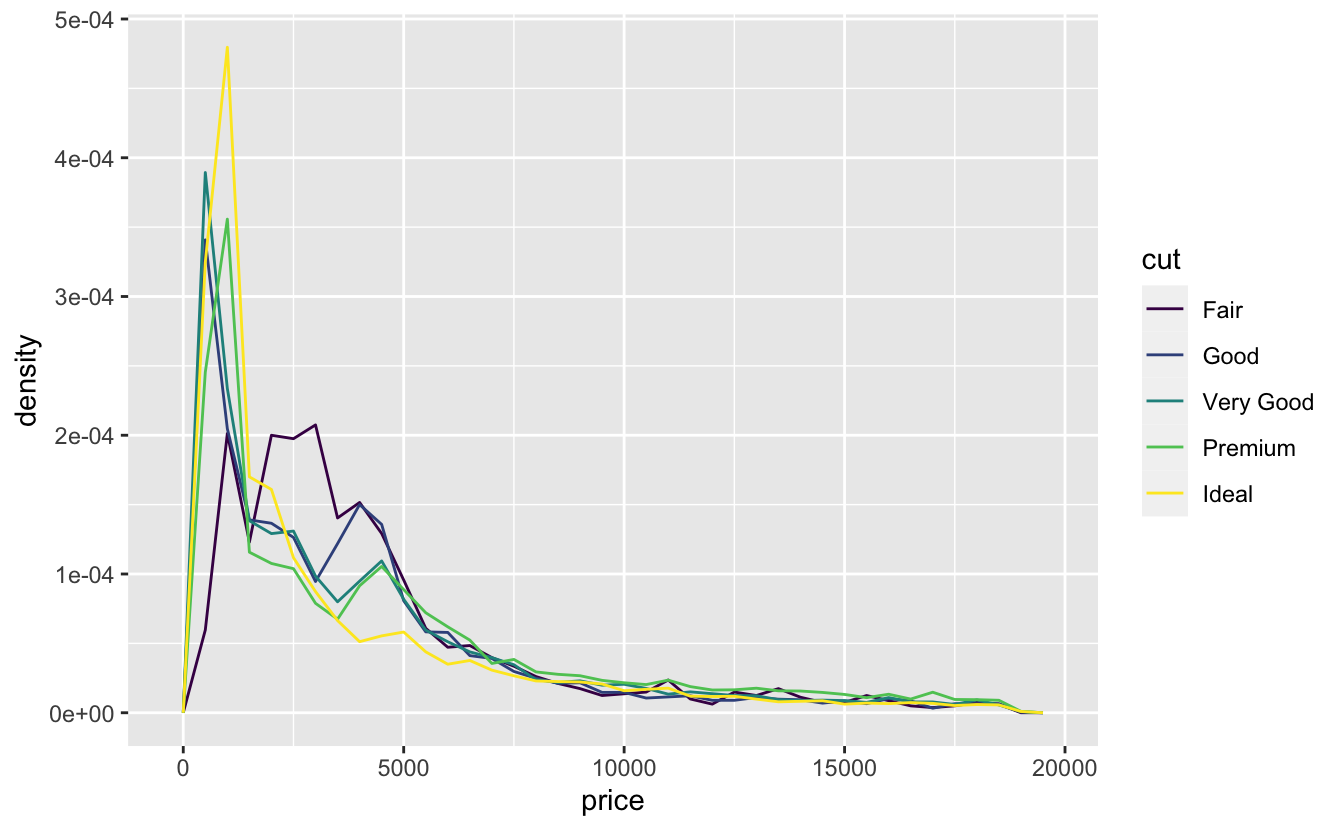
이 플롯에는 꽤 놀라운 점이 있다. 그것은 fair 인 다이아몬드(가장 낮은 품질)가 가장 높은 평균 가격을 가진다는 것이다. 그건 아마도 이 빈도 다각형에는 작업해야 하는 부분이 아직 남아 있어서, 당장은 해석하기가 어렵기 때문일 것이다.
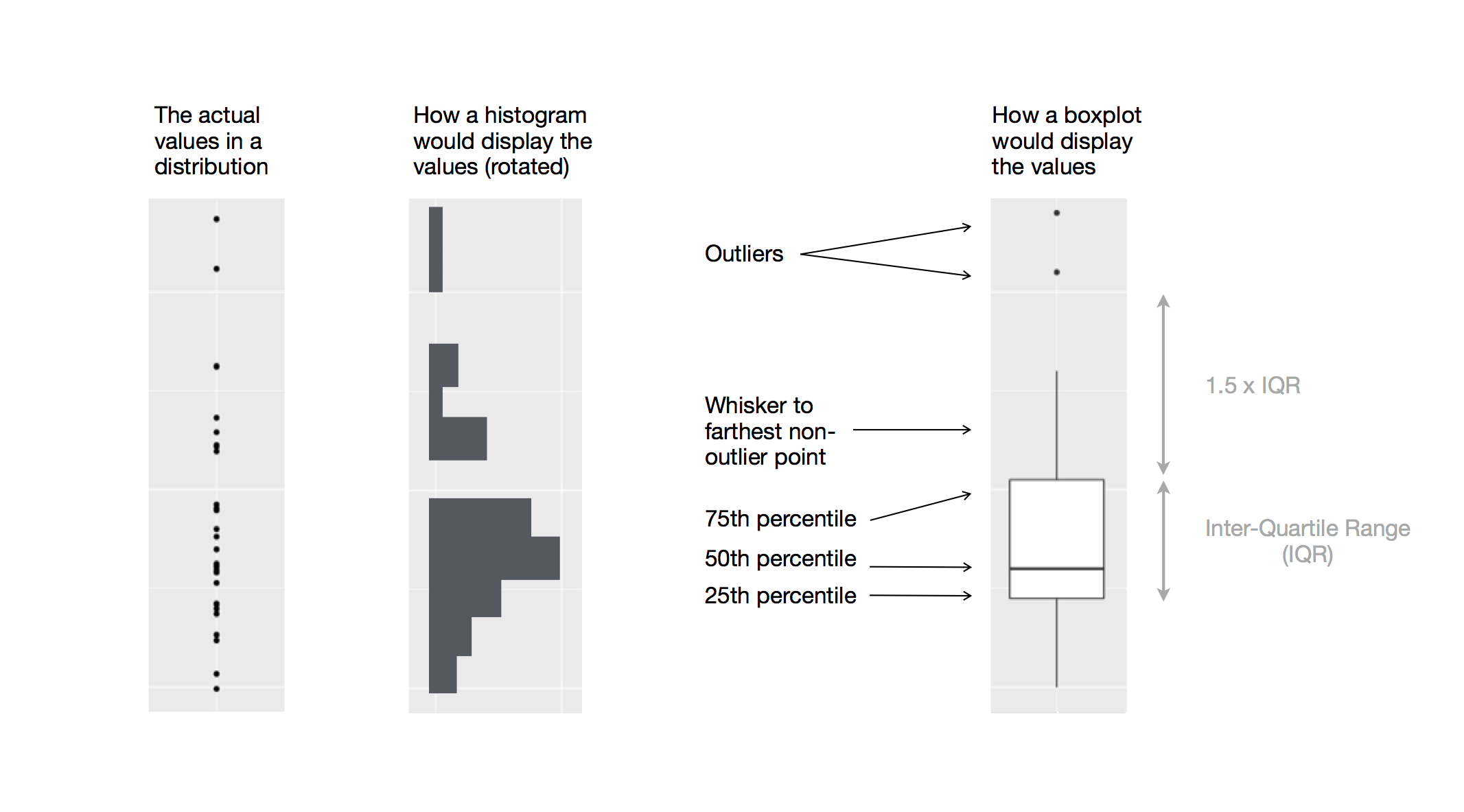
범주형 변수로 구분된 연속형 변수의 분포를 나타내는 또 다른 방법은 박스플롯(boxplot)이다. 박스플롯은 값의 분포를 시각적으로 간편하게 보여줄 수 있는 형태로 많은 통계학자가 사용하는 방법이다. 박스플롯은 다음의 것들로 구성된다.
사분위 수 범위(IQR)이라는 이름을 가진 길이의 25번째 백분위 수에서 75번째 백분위 수까지 이어진 상자. 분포의 중앙값(즉, 50번째 백분위 수)을 표시하는 상자의 가운데 위치한 선. 이 세 개의 선은 분포의 대략적인 범위와 분포의 중앙값이 대칭인지 또는 한쪽으로 치우쳤는지를 나타낸다.
상자의 가장자리에서 IQR 의 1.5배 이상 떨어진 관측값을 나타내는 점. 이렇게 멀리 떨어진 점들은 일반적이지 않기 때문에 개별적으로 표시된다.
상자의 양끝에서 뻗어나와 가장멀리 떨어진 이상값이 아닌 점까지 이어진 선.
geom_boxplot() 을 사용하여 컷팅에 따른 가격의 분포를 살펴보자.:
ggplot(data = diamonds, mapping = aes(x = cut, y = price)) +
geom_boxplot()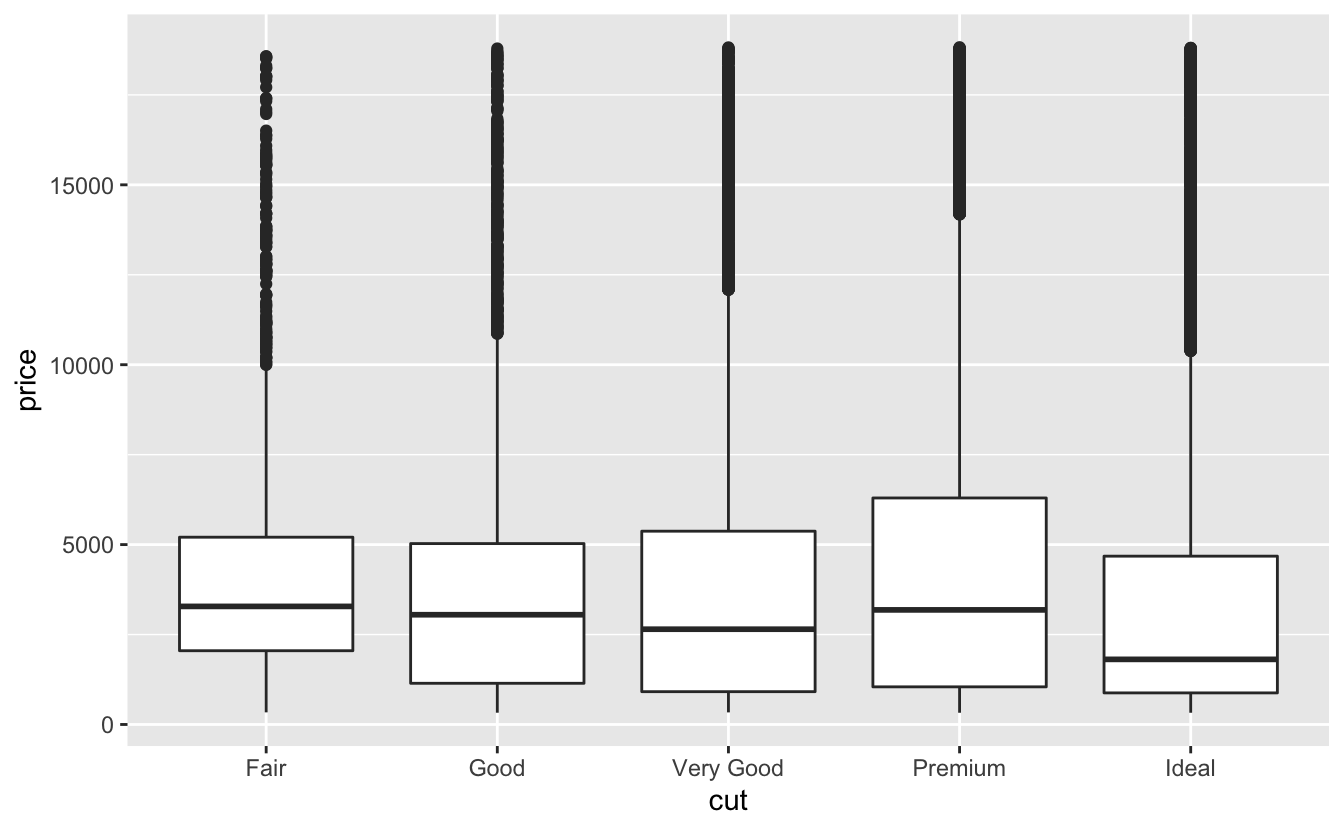
박스 플롯은 분포에 대해 더 적은 정보를 확인할 수 있지만, 간단하므로 쉽게 비교할 수 있다. (또한, 한 개의 플롯에 더 적합하다.) 이 플롯은 ‘더 좋은 품질의 다이아몬드가 평균적으로 더 저렴하다’는 직관에 반하는 사실을 뒷받침한다. 그 이유는 연습문제에서 파악해볼 것이다.
cut 은 순서가 있는 팩터형 변수이다. fair 는 good 보다 좋지 않고, good 은 very good 보다 좋지 않으며 그 이후도 동일한 순서를 따른다. 대부분의 범주형 변수에는 이러한 고유한 순서가 없으므로 순서를 변경하여 더 유용한 정보를 주도록 표현할 수 있다. 이를 위한 한 가지 방법은 reorder() 함수를 사용하는 것이다.
예를 들어 mpg 데이터셋의 class (차종)를 살펴보자. 차종에 따라 고속도로 주행 거리가 어떻게 달라지는지 알아보고자 한다.
ggplot(data = mpg, mapping = aes(x = class, y = hwy)) +
geom_boxplot()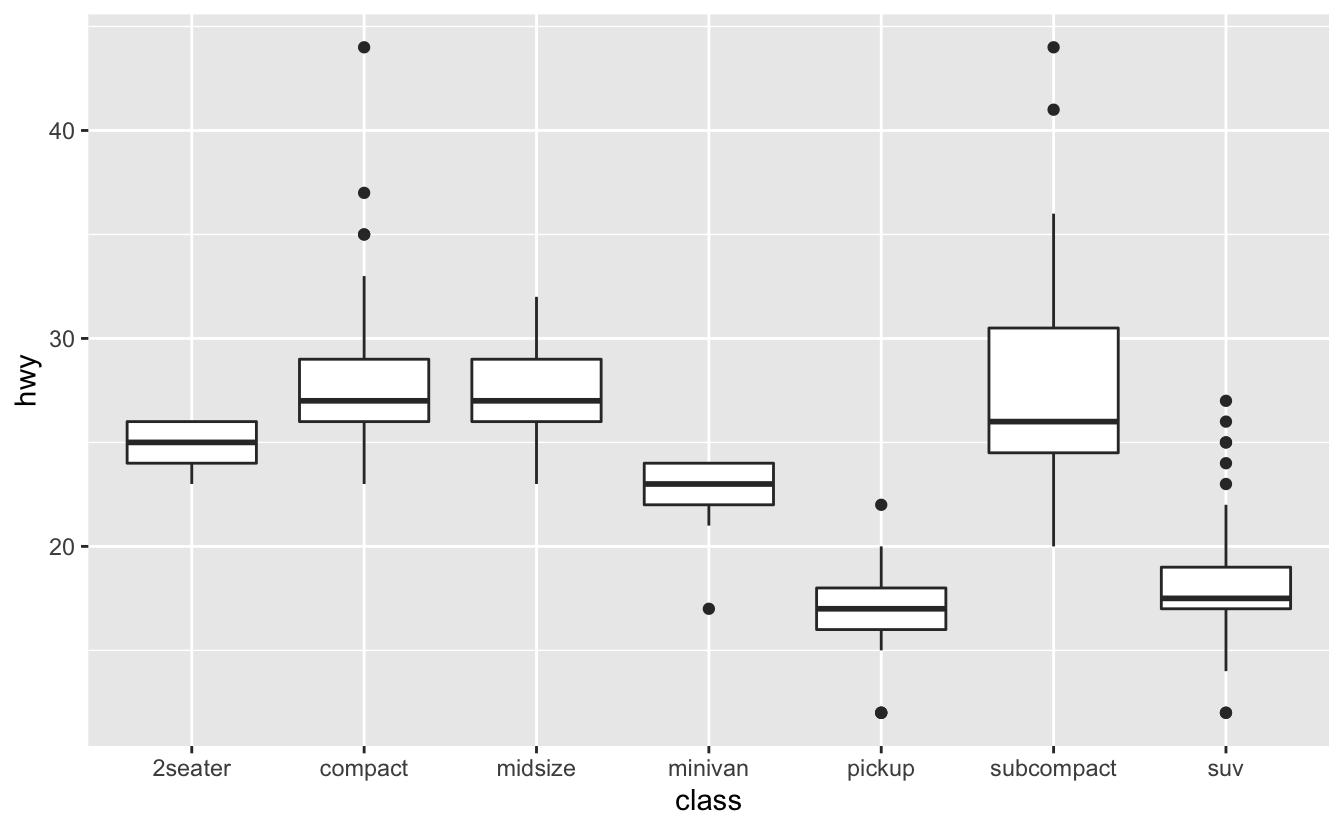
추세를 더욱 쉽게 파악하기 위해 hwy 변수의 중간값을 기준으로 class 변수의 순서를 변경할 수 있다.
ggplot(data = mpg) +
geom_boxplot(mapping = aes(x = reorder(class, hwy, FUN = median), y = hwy))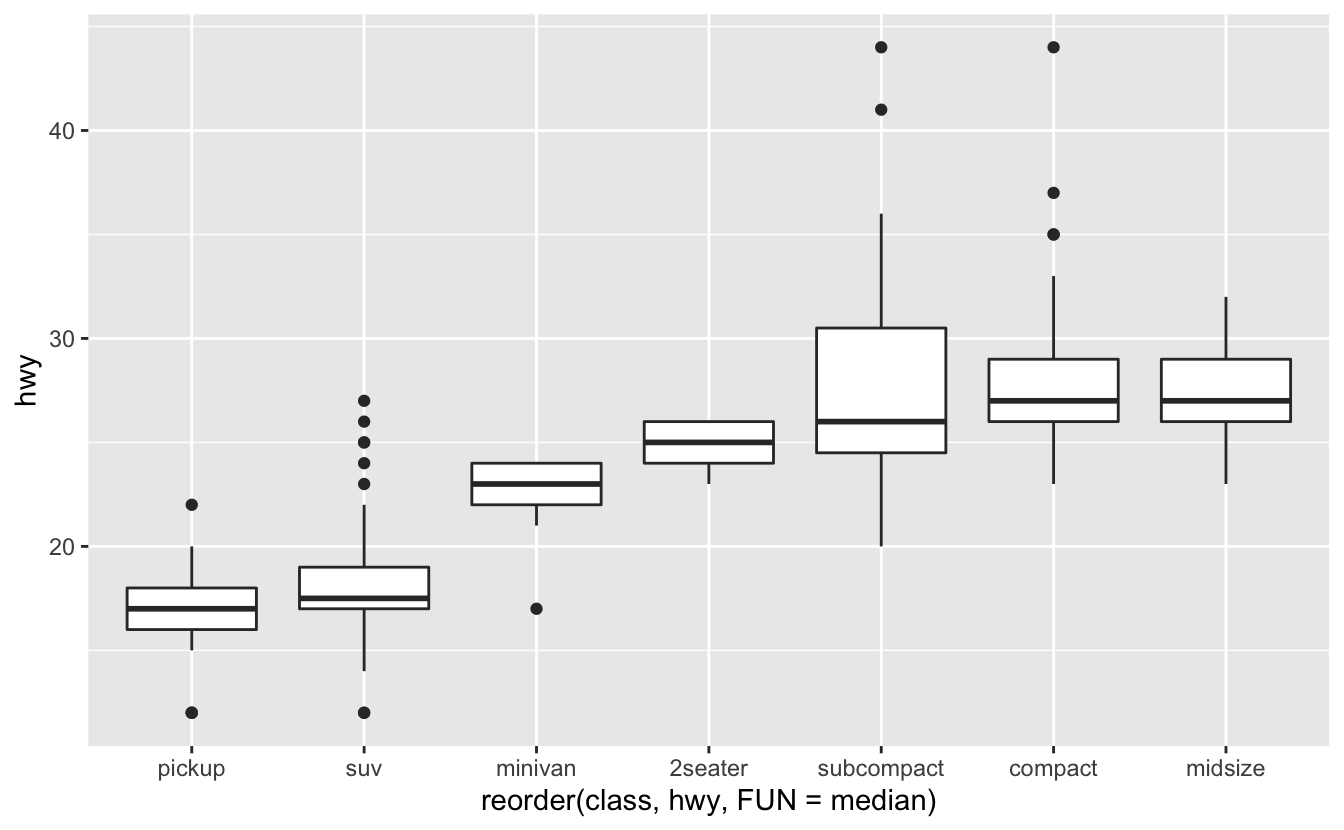
변수의 이름이 긴 경우 geom_boxplot() 을 90° 회전시키면 더 잘 나타낼 수 있다. coord_flip() 을 사용하여 다음과 같이 나타낼 수 있다.
ggplot(data = mpg) +
geom_boxplot(mapping = aes(x = reorder(class, hwy, FUN = median), y = hwy)) +
coord_flip()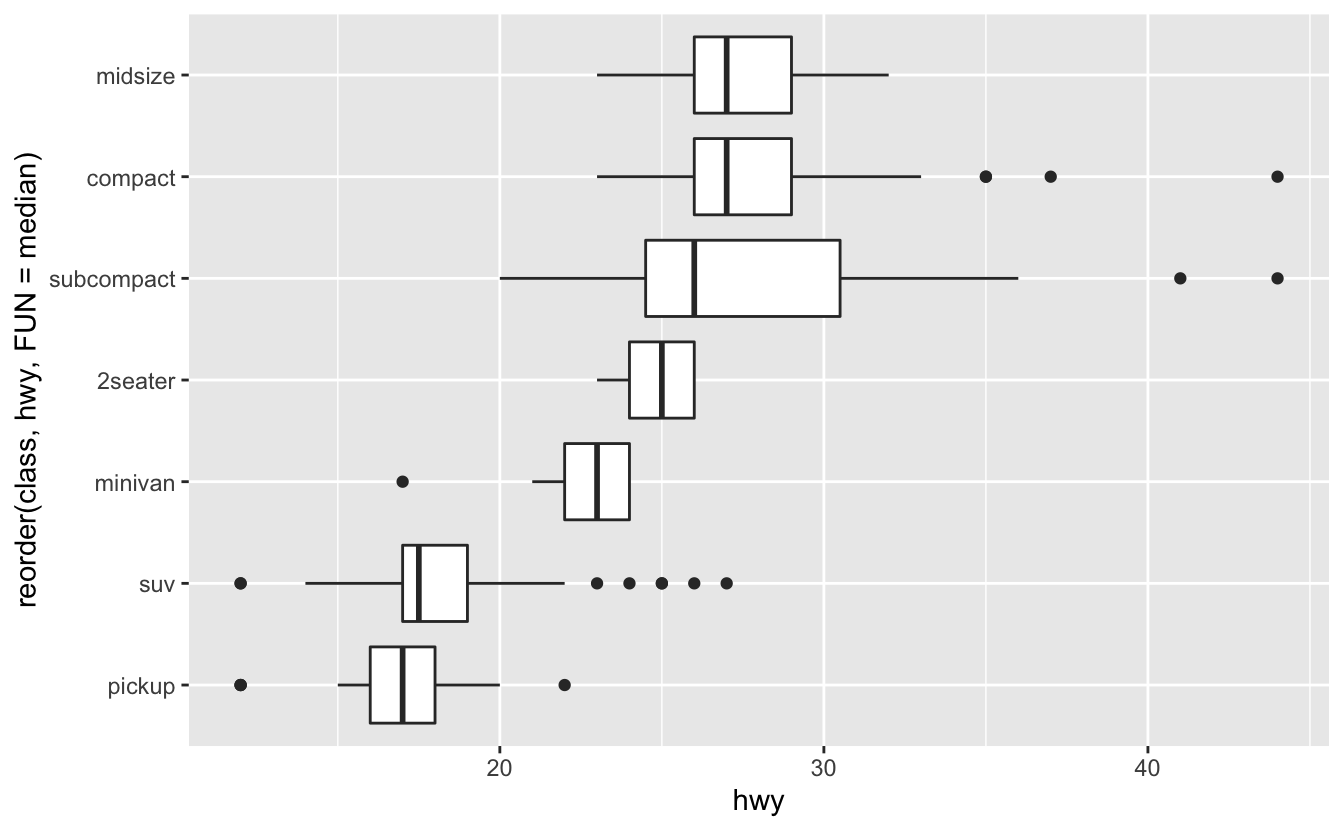
11.5.1.1 Exercises
Use what you’ve learned to improve the visualisation of the departure times of cancelled vs. non-cancelled flights.
What variable in the diamonds dataset is most important for predicting the price of a diamond? How is that variable correlated with cut? Why does the combination of those two relationships lead to lower quality diamonds being more expensive?
Install the ggstance package, and create a horizontal boxplot. How does this compare to using
coord_flip()?One problem with boxplots is that they were developed in an era of much smaller datasets and tend to display a prohibitively large number of “outlying values”. One approach to remedy this problem is the letter value plot. Install the lvplot package, and try using
geom_lv()to display the distribution of price vs cut. What do you learn? How do you interpret the plots?Compare and contrast
geom_violin()with a facettedgeom_histogram(), or a colouredgeom_freqpoly(). What are the pros and cons of each method?If you have a small dataset, it’s sometimes useful to use
geom_jitter()to see the relationship between a continuous and categorical variable. The ggbeeswarm package provides a number of methods similar togeom_jitter(). List them and briefly describe what each one does.
11.5.2 범주형 변수 두 개
범주형 변수들의 공변동을 시각화하려면 각 조합에 대한 관측값의 수를 세어야 한다. 이를 위한 한 가지 방법은 내장된 함수인 geom_count() 를 이용하는 것이다.
ggplot(data = diamonds) +
geom_count(mapping = aes(x = cut, y = color))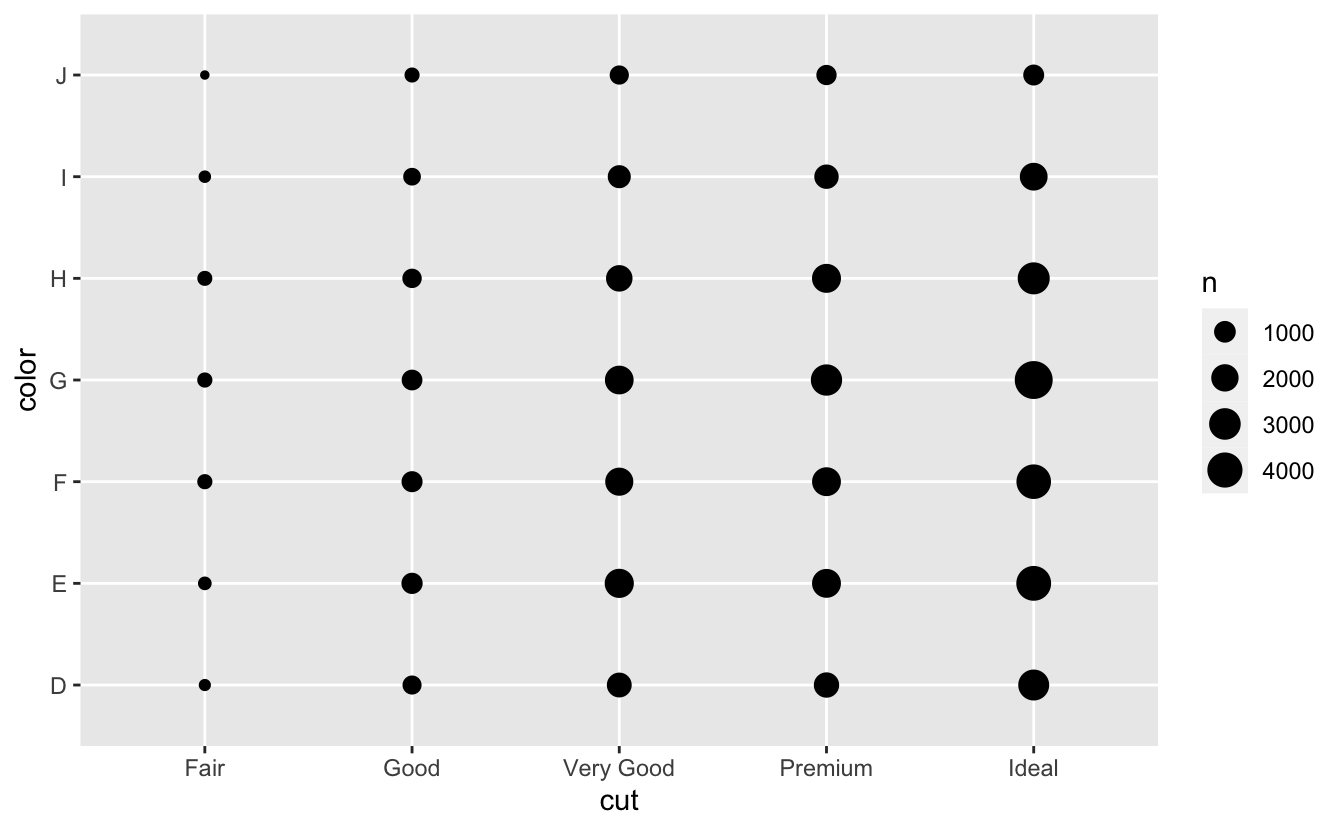
플롯에서 원의 크기는 각 값의 조합에서 발생한 관측값의 수를 나타낸다. 공변동은 특정 x 값과 y 값 사이에 강한 상관관계로 나타날 것이다.
또 다른 방법은 dplyr 로 빈도수를 계산하는 것이다.
diamonds %>%
count(color, cut)
#> # A tibble: 35 × 3
#> color cut n
#> <ord> <ord> <int>
#> 1 D Fair 163
#> 2 D Good 662
#> 3 D Very Good 1513
#> 4 D Premium 1603
#> 5 D Ideal 2834
#> 6 E Fair 224
#> # … with 29 more rows그런 다음 geom_tile() 함수와 fill 심미성으로 시각화한다.
diamonds %>%
count(color, cut) %>%
ggplot(mapping = aes(x = color, y = cut)) +
geom_tile(mapping = aes(fill = n))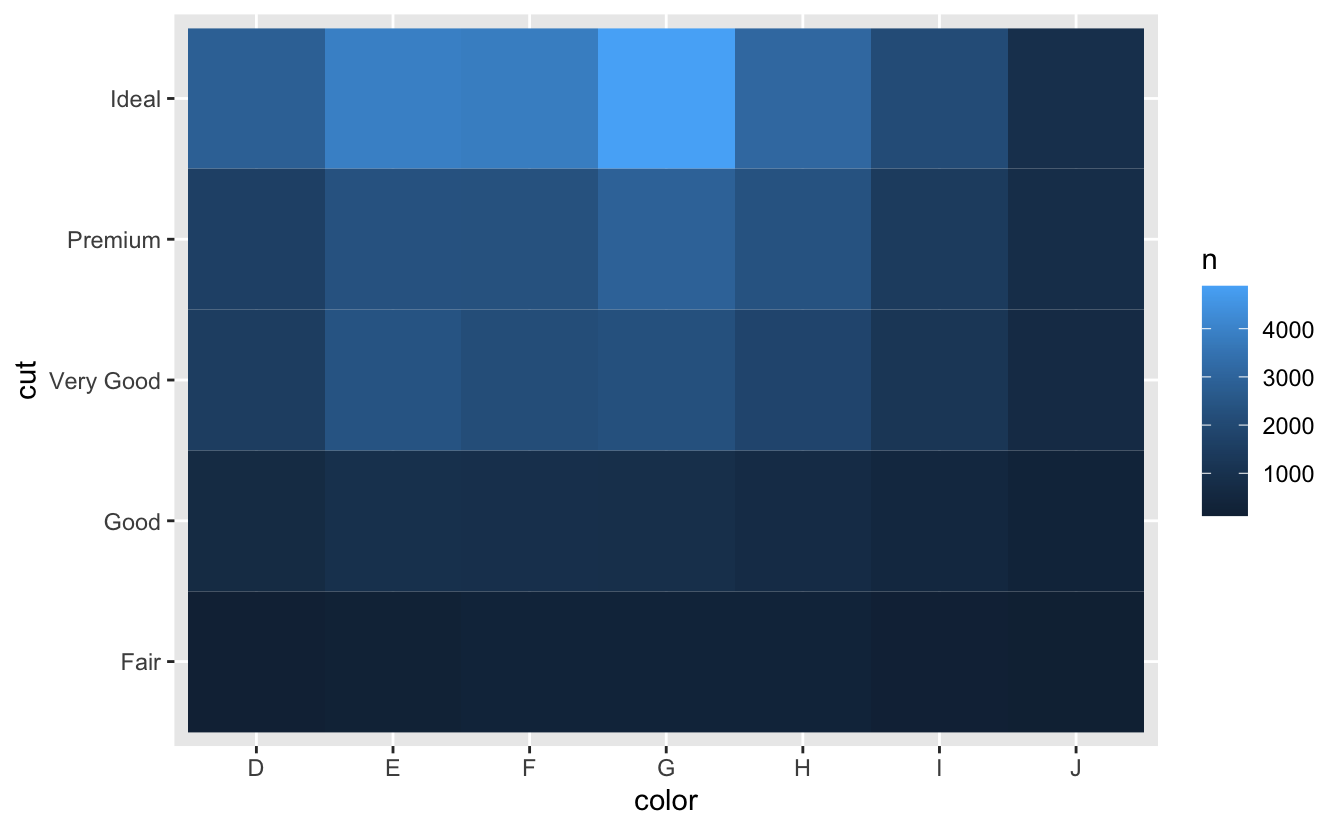
범주형 변수에서 순서가 없는 경우 흥미로운 패턴을 좀 더 명확하게 나타내기 위해 seriation 패키지를 사용하여 행과 열을 동시에 정렬할 수 있다. 플롯이 이 보다 더 큰 경우 대화형 플롯을 만드는 d3heatmap 또는 heatmaply 패키지를 사용해 볼 수 있다.
11.5.2.1 Exercises
How could you rescale the count dataset above to more clearly show the distribution of cut within colour, or colour within cut?
Use
geom_tile()together with dplyr to explore how average flight delays vary by destination and month of year. What makes the plot difficult to read? How could you improve it?Why is it slightly better to use
aes(x = color, y = cut)rather thanaes(x = cut, y = color)in the example above?
11.5.3 연속형 변수 두 개
두 개의 연속형 변수 사이의 공변동을 시각화하는 좋은 방법 중 하나(geom_ point() 로 산점도를 그리는 것)는 앞서 배웠다. 점들의 패턴으로 공변동을 확인할 수 있다. 예를 들어 캐럿의 크기와 다이아몬드의 가격 사이에 기하급수적인 관계가 있다는 것을 확인할 수 있다.
ggplot(data = diamonds) +
geom_point(mapping = aes(x = carat, y = price))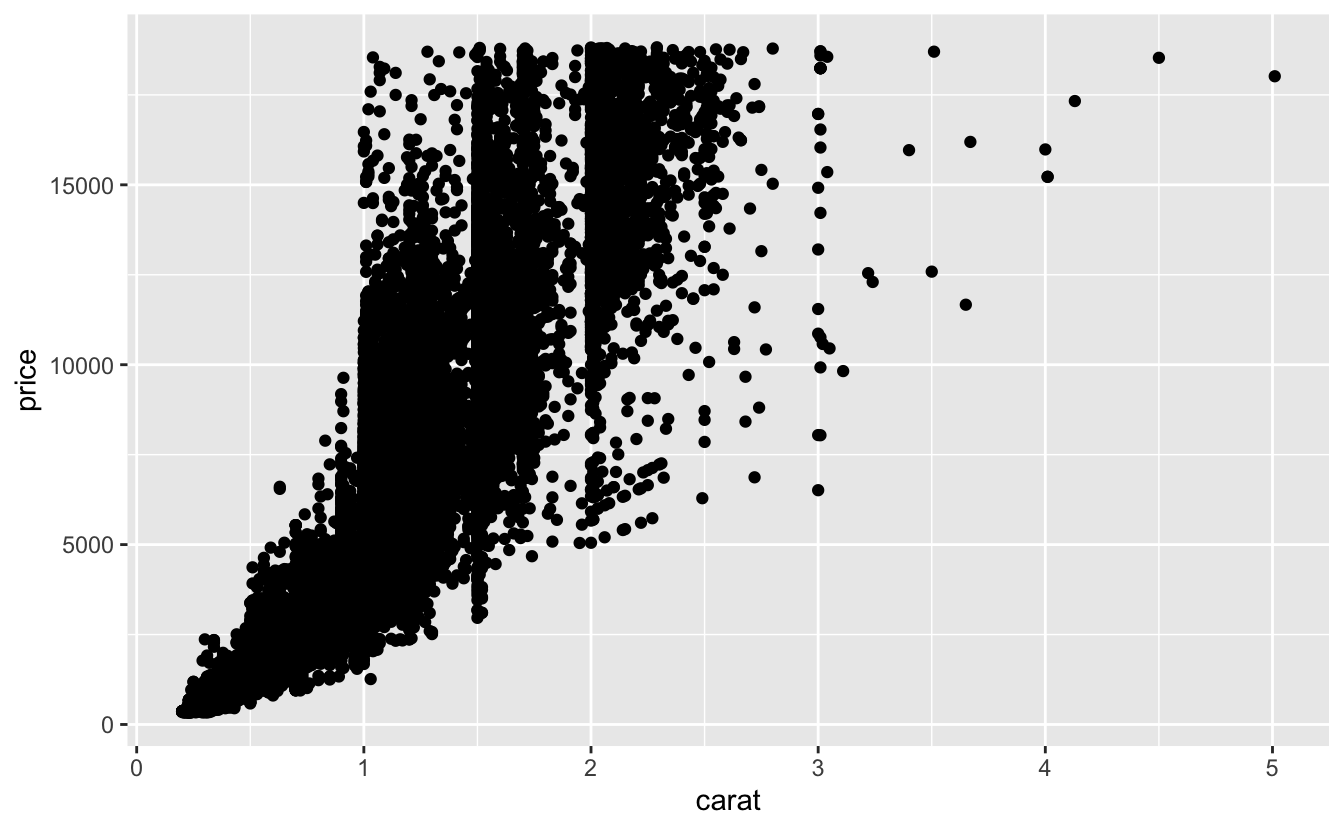
산점도는 데이터셋의 크기가 커지면 (앞의 산점도처럼) 점들이 겹치고 획일적인 검은색 영역으로 쌓이기 때문에 덜 유용해진다. 이러한 문제를 해결하기 위해 alpha 심미성을 사용하여 투명도를 추가하는 방법에 대해서는 앞서 살펴보았다.
ggplot(data = diamonds) +
geom_point(mapping = aes(x = carat, y = price), alpha = 1 / 100)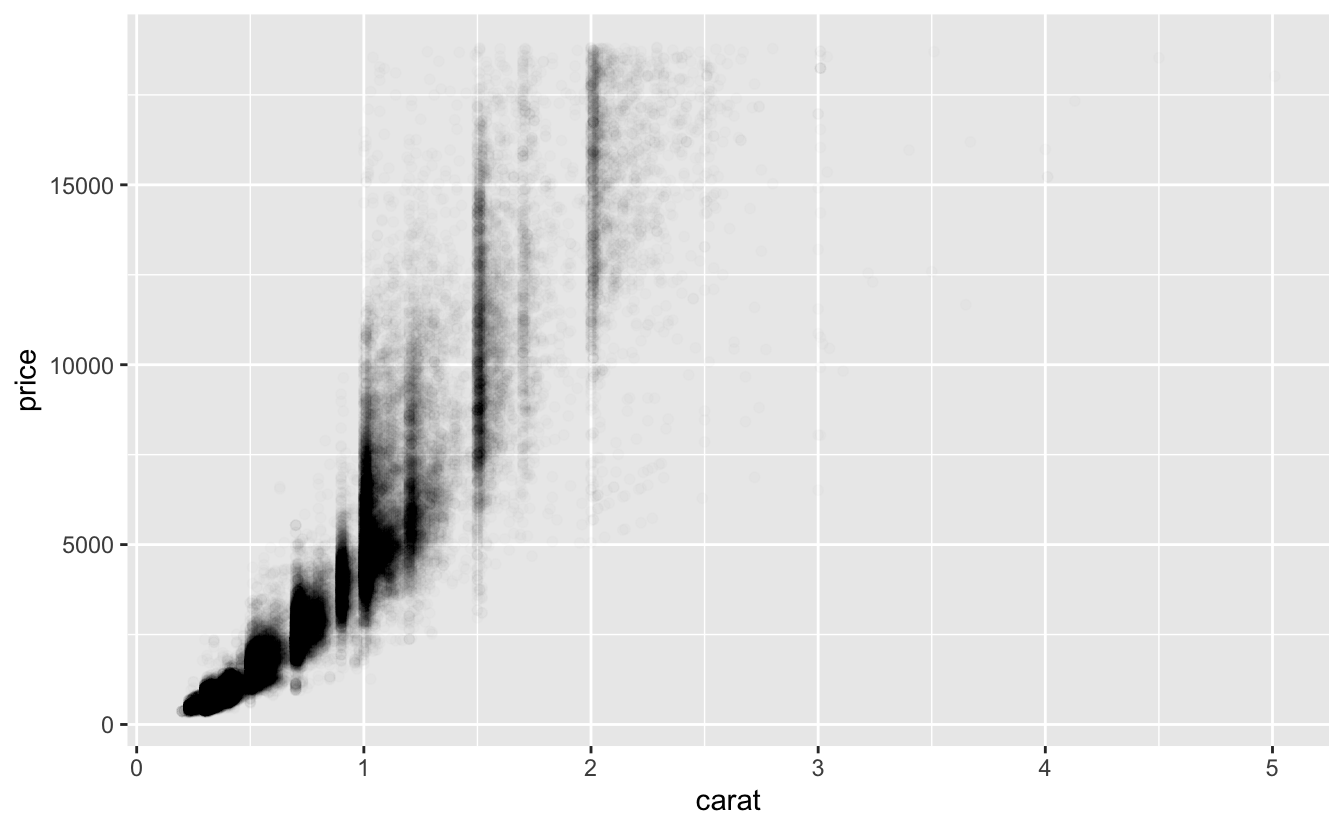
그러나 매우 큰 데이터셋에서 투명도 사용은 어려울 수 있다. 또 다른 해결 방법 은 빈(bin)을 사용하는 것이다. 이전에는 geom_histogram() 과 geom_freqpoly() 에서 1차원의 빈을 사용했다. 이제 geom_bin2d() 와 geom_hex() 함수에서 2차원의 빈을 사용하는 방법을 배울 것이다.
geom_bin2d() 와 geom_hex() 는 좌표 평면을 2D 빈으로 나눈 후, 각 빈에 몇 개의 점이 해당하는지 나타내기 위해 색상 채우기를 사용한다. geom_bin2d() 는 직사각형 빈을 만들고, geom_hex()는 육각형 빈을 만든다. geom_hex() 를 사용하기 위해 서는 hexbin 패키지를 설치해야 한다.
ggplot(data = smaller) +
geom_bin2d(mapping = aes(x = carat, y = price))
# install.packages("hexbin")
ggplot(data = smaller) +
geom_hex(mapping = aes(x = carat, y = price))
#> Warning: Computation failed in `stat_binhex()`:
#> The `hexbin` package is required for `stat_binhex()`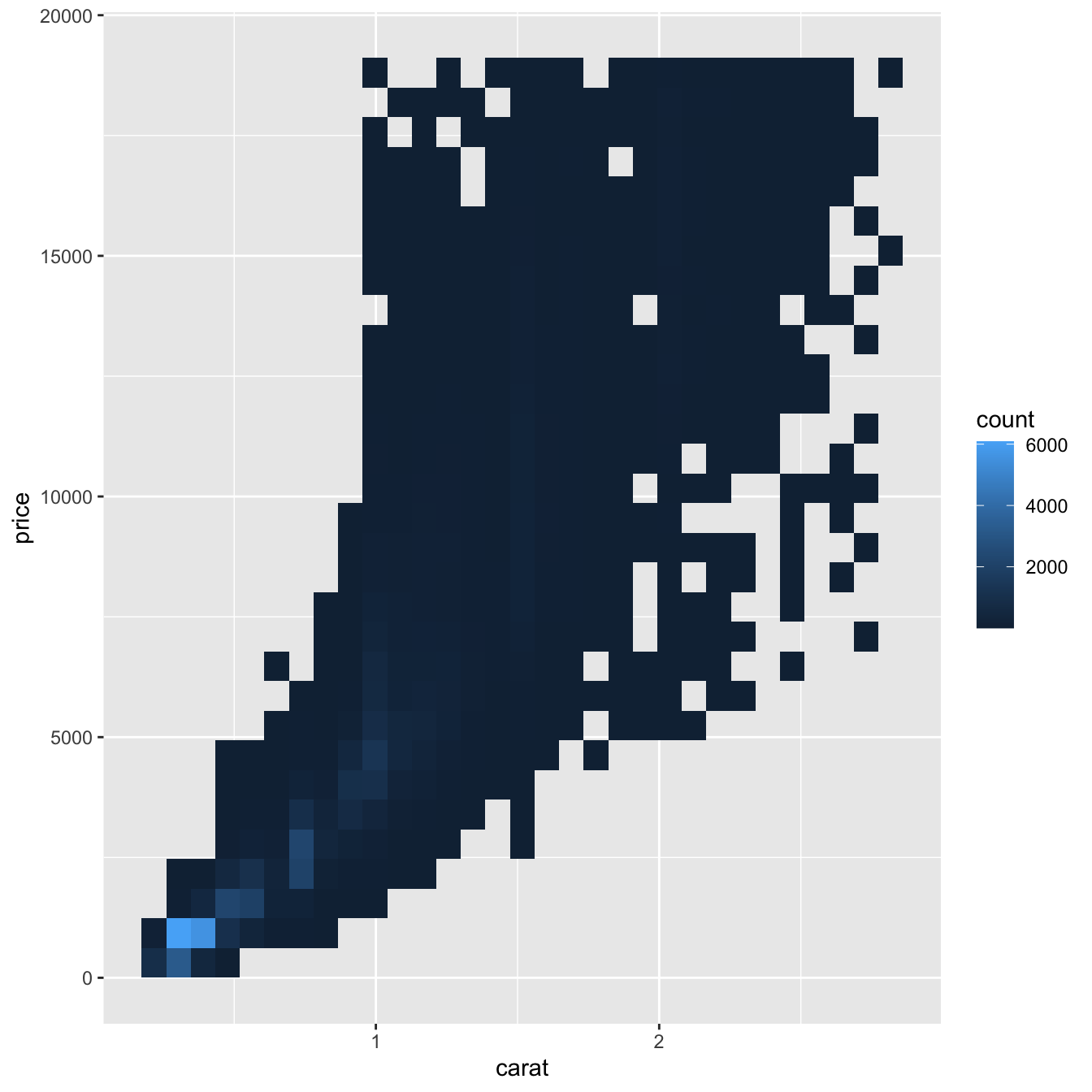

또 다른 옵션은 하나의 연속 변수를 그룹화하여 범주형 변수처럼 만드는 것이 다. 그렇게 하면 이전에 배웠던 범주형 변수와 연속형 변수의 조합을 시각화하 는 방법 중 한 가지를 사용할 수 있다. 예를 들어 carat 변수를 그룹화한 후, 각 그룹에 대해 박스 플롯을 그릴 수 있다.
ggplot(data = smaller, mapping = aes(x = carat, y = price)) +
geom_boxplot(mapping = aes(group = cut_width(carat, 0.1)))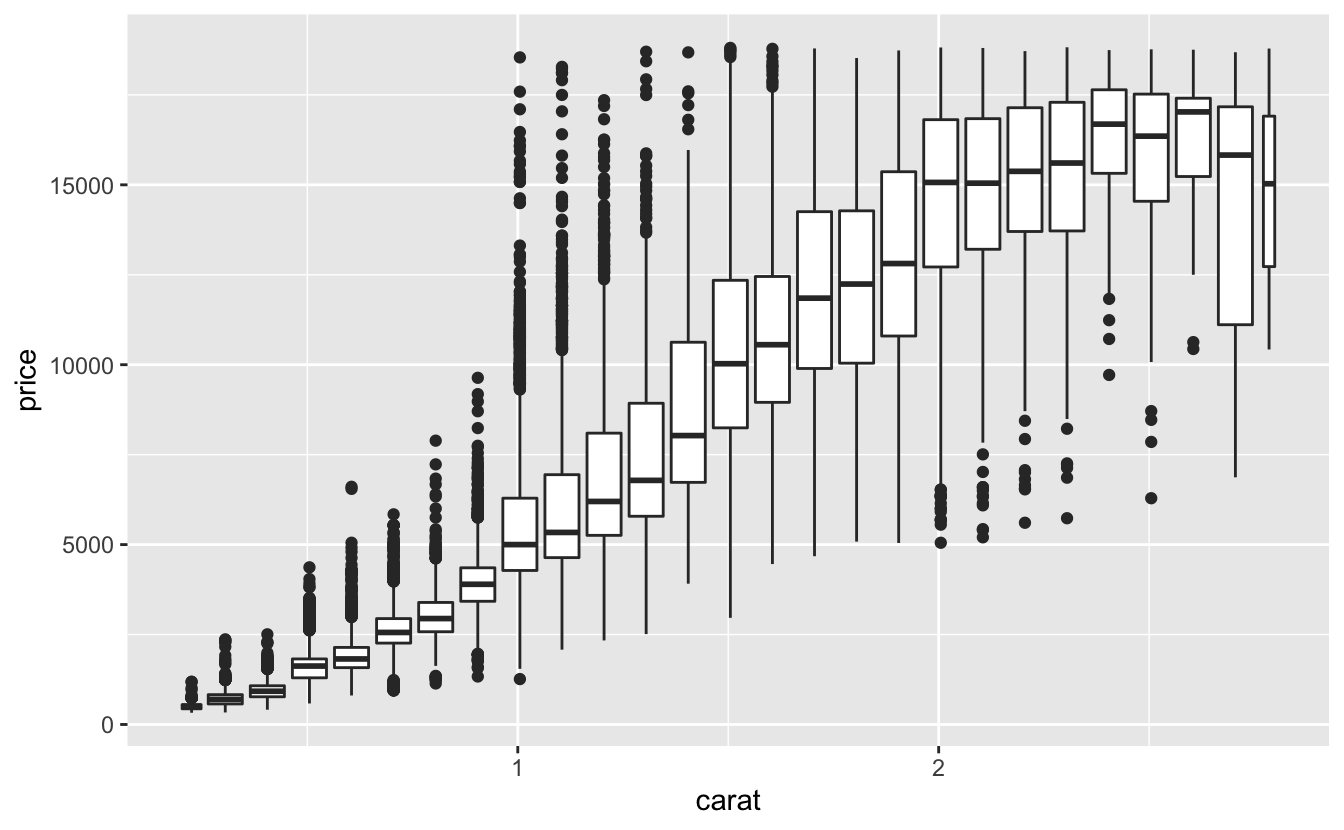
여기에서 사용된 cut_width(x, width) 함수는 x 를 빈 너비인 width 로 나누어준다. 기본적으로 박스 플롯은 (이상값의 수와는 별개로) 얼마나 많은 관측값이 있는지와 관계없이 동일하게 보이기 때문에 각 박스 플롯이 얼마나 많은 수의 점을 요약하는지는 알기 어렵다. 이를 보여줄 수 있는 한 가지 방법은 varwidth = TRUE 를 사용하여
박스플롯의 너비를 점의 개수와 비례하도록 설정하는 것이다.
또 다른 방법은 각 빈에 대략적으로 같은 수의 점을 표시하는 것이다. 이는 cut_number() 를 사용하면 된다.
ggplot(data = smaller, mapping = aes(x = carat, y = price)) +
geom_boxplot(mapping = aes(group = cut_number(carat, 20)))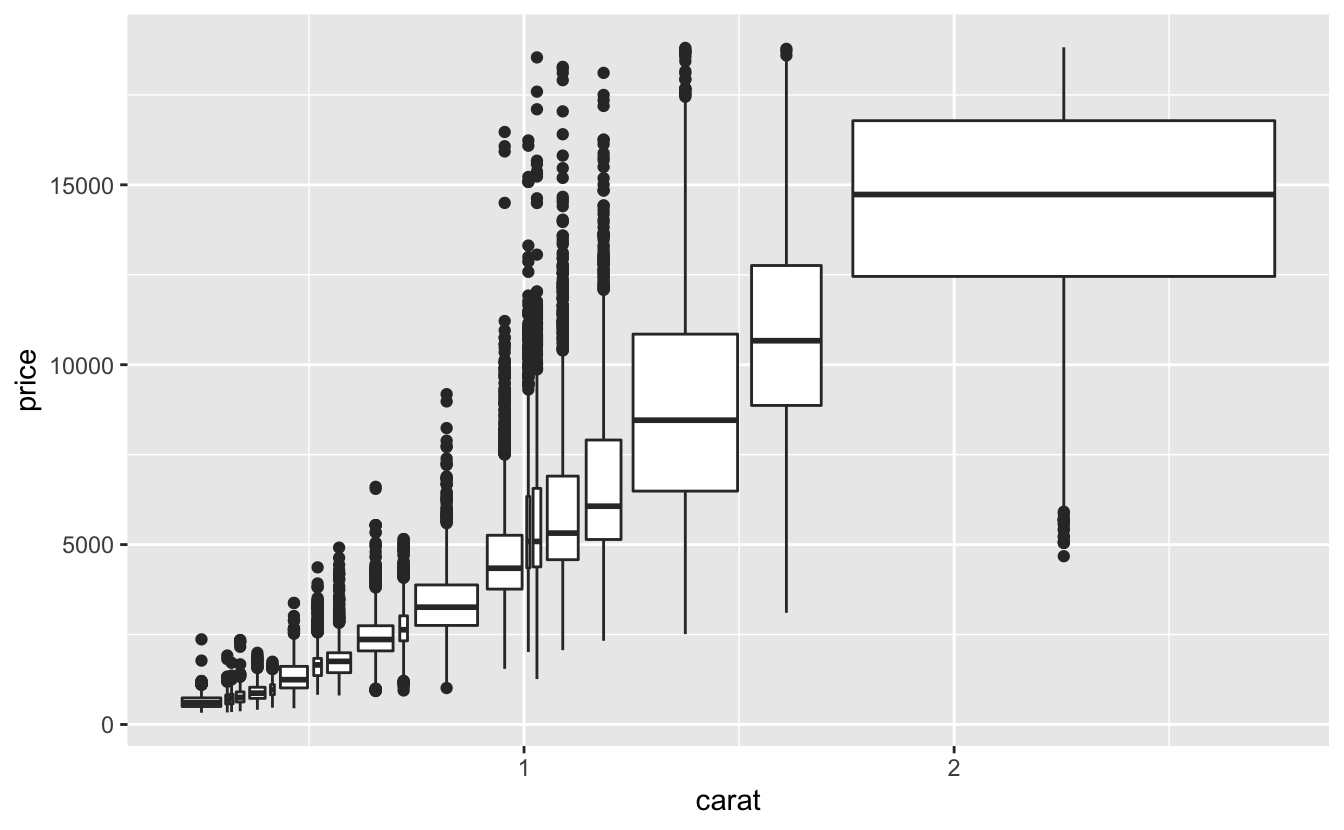
11.5.3.1 Exercises
Instead of summarising the conditional distribution with a boxplot, you could use a frequency polygon. What do you need to consider when using
cut_width()vscut_number()? How does that impact a visualisation of the 2d distribution ofcaratandprice?Visualise the distribution of carat, partitioned by price.
How does the price distribution of very large diamonds compare to small diamonds? Is it as you expect, or does it surprise you?
Combine two of the techniques you’ve learned to visualise the combined distribution of cut, carat, and price.
-
Two dimensional plots reveal outliers that are not visible in one dimensional plots. For example, some points in the plot below have an unusual combination of
xandyvalues, which makes the points outliers even though theirxandyvalues appear normal when examined separately.ggplot(data = diamonds) + geom_point(mapping = aes(x = x, y = y)) + coord_cartesian(xlim = c(4, 11), ylim = c(4, 11))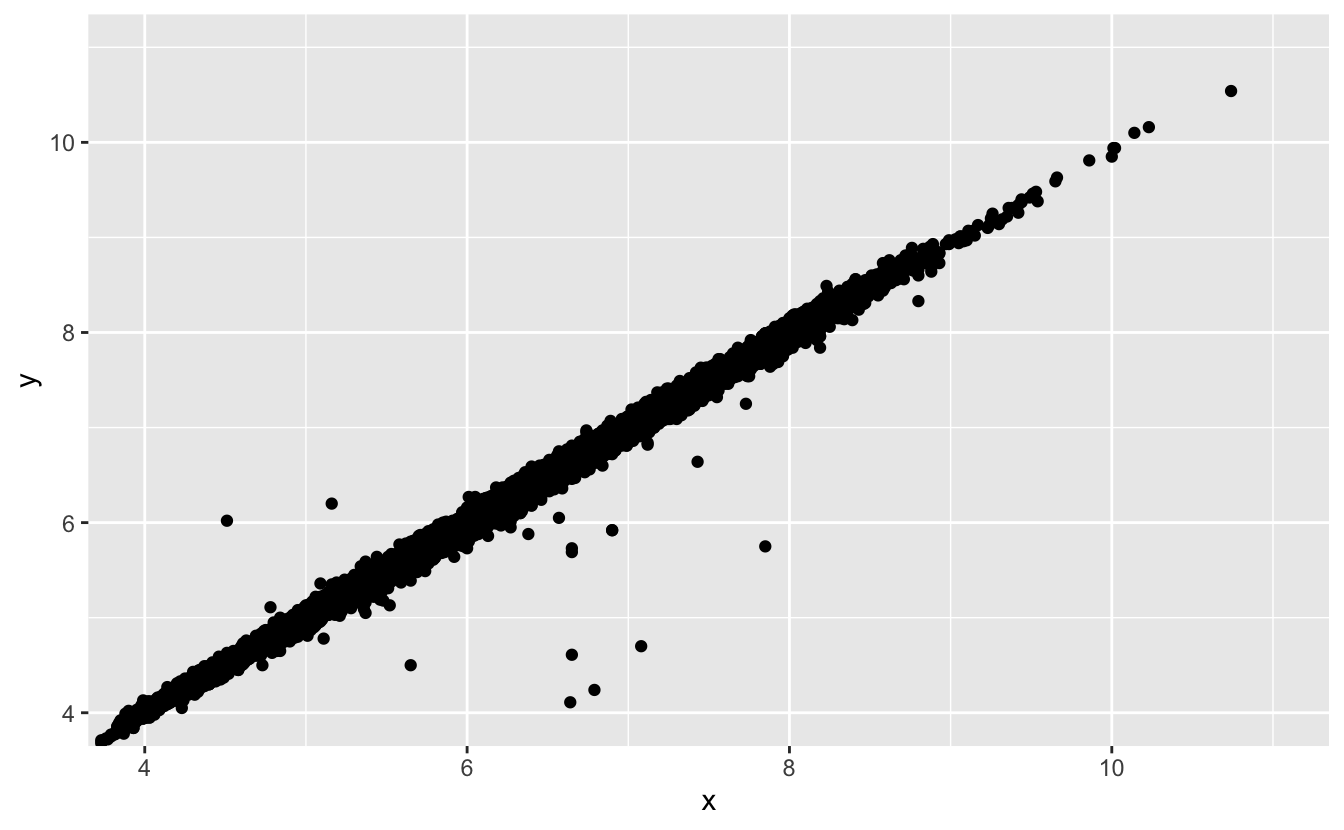
Why is a scatterplot a better display than a binned plot for this case?
11.6 패턴과 모델
데이터의 패턴은 상관관계에 대한 단서를 제공한다. 두 변수 사이에 규칙적인 관계가 존재하면 데이터의 패턴으로 나타난다. 패턴을 발견하게 되면 스스로 질문해보자.
이 패턴은 우연의 일치(즉, 랜덤한 가능성) 때문인가?
패턴이 내포하는 상관관계를 어떻게 설명할 수 있는가?
패턴이 내포하는 상관관계는 얼마나 강한가?
다른 변수가 그 상관관계에 영향을 줄 수 있는가?
데이터의 개별 하위집단을 살펴보면 상관관계가 변경되는가?
Old Faithful 분출 시간과 분출 사이의 시간 사이의 산점도는 분출 사이의 대기 시간이 길수록 분출 시간도 길어지는 패턴을 보인다.
ggplot(data = faithful) +
geom_point(mapping = aes(x = eruptions, y = waiting))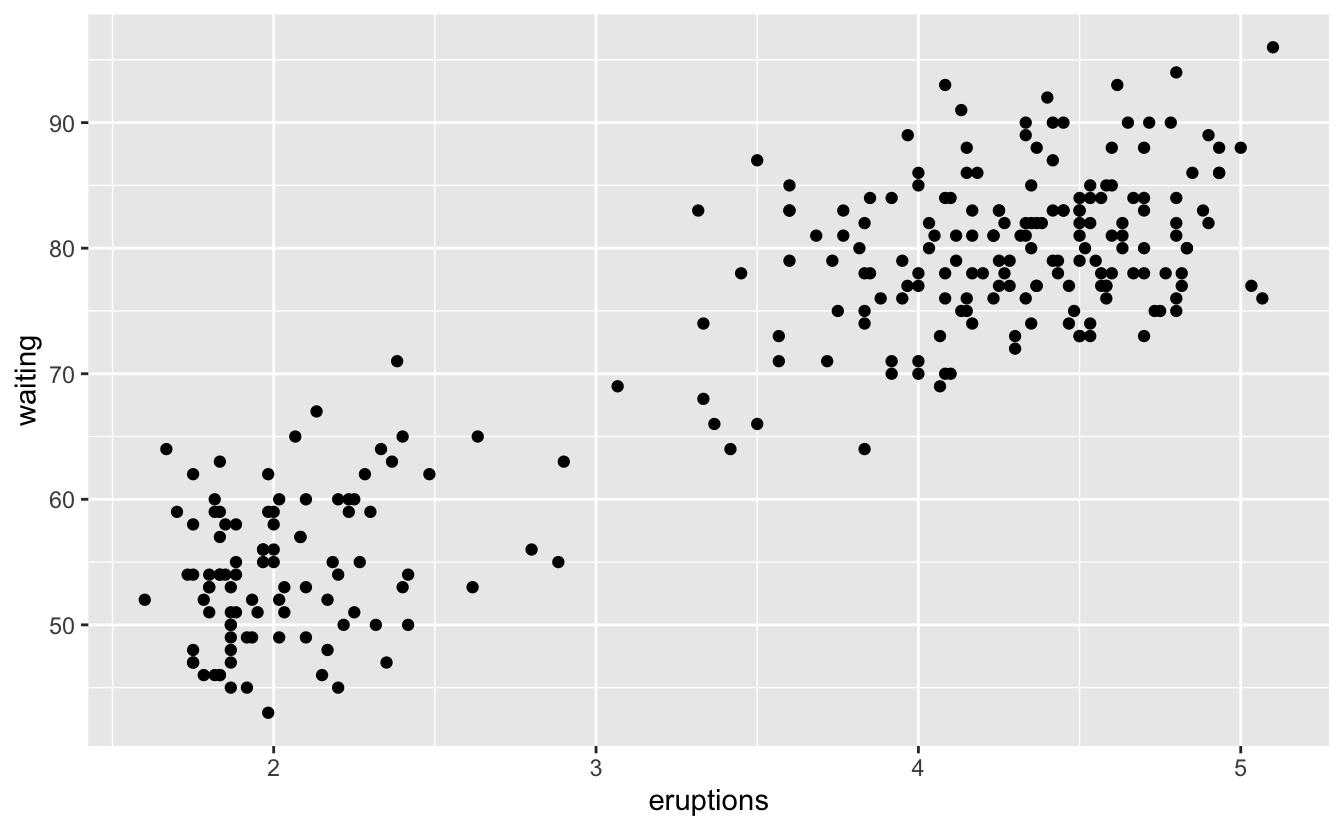
패턴은 공변동을 나타내기 때문에 데이터 과학자에게 가장 유용한 도구 중 하나 이다. 변동을 불확실성이 만드는 현상으로 생각한다면 공변동은 불확실성을 감소시키는 현상이다. 두 개의 변수가 함께 변동하면 한 변수의 값을 사용하여 다른 변수의 값을 잘 예측할 수 있다. 인과관계(특별한 경우)로 인해 공변동이 생기는 경우, 한 변수의 값을 다른 변수의 값을 통제하는 데 사용할 수 있다.
모델은 데이터에서 패턴을 추출하는 도구이다. 예를 들어 다이아몬드 데이터를 생각해보자. 컷팅과 캐럿 그리고 캐럿과 가격은 밀접하게 관련되어 있으므로 컷팅과 가격의 상관관계를 이해하기 어렵다. 모델을 활용하여 가격과 캐럿 간의 매우 강력한 상관관계를 제거하면 남아있는 중요한 세부 요소들을 탐색할 수 있다. 다음 코드에서는 carat 으로 price 를 예측하는 모델을 적합시킨 다음, 잔차(예측값과 실제값의 차이)를 계산한다. 캐럿의 효과가 제거되면 잔차는 다이아몬드의 가격에 대한 관점을 제공한다.
library(modelr)
mod <- lm(log(price) ~ log(carat), data = diamonds)
diamonds2 <- diamonds %>%
add_residuals(mod) %>%
mutate(resid = exp(resid))
ggplot(data = diamonds2) +
geom_point(mapping = aes(x = carat, y = resid))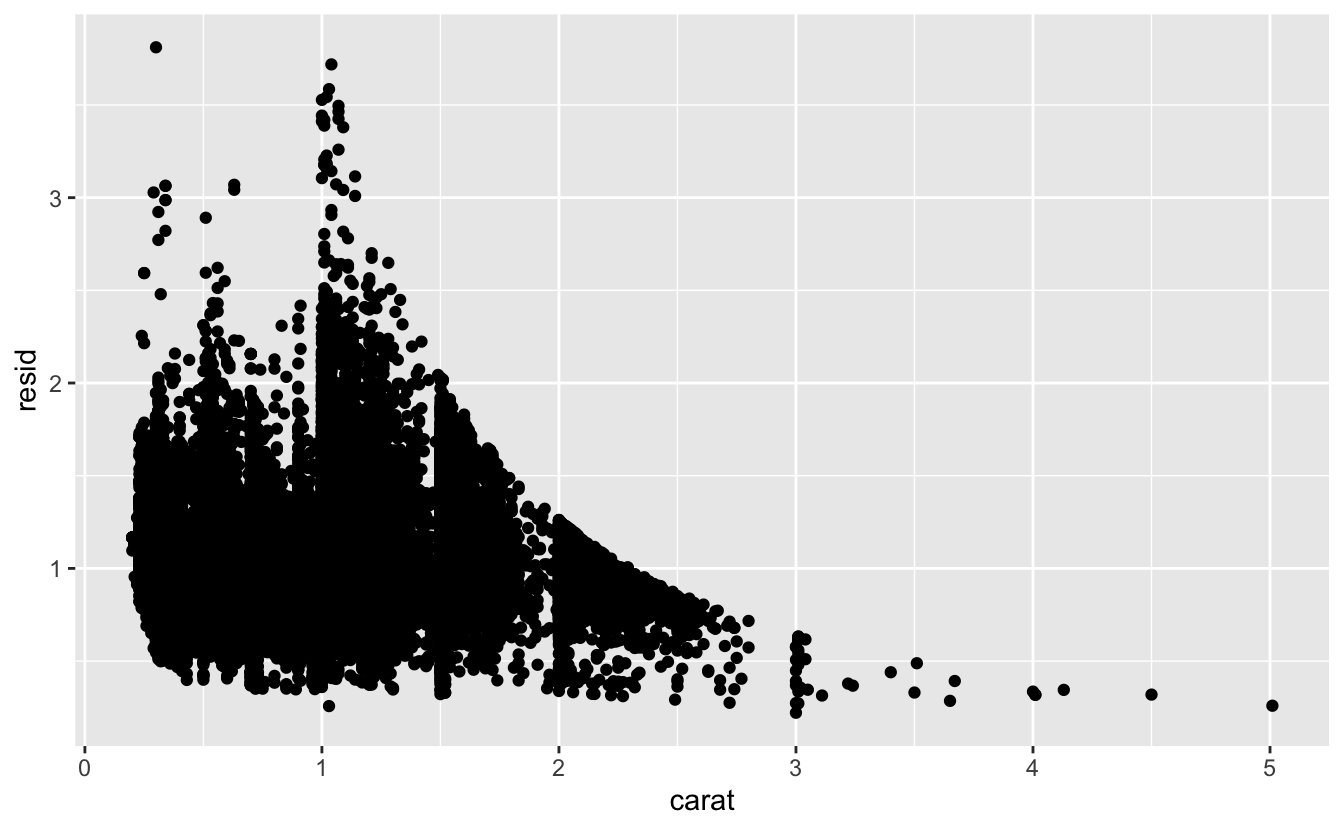
캐럿과 가격의 강한 상관관계를 제거했기 때문에, 이제 예상할 수 있는 커팅과 가격의 상관관계(다이아몬드의 크기에 비례하여 우수한 품질의 다이아몬드가 더 비싸다)를 파악할 수 있다.
ggplot(data = diamonds2) +
geom_boxplot(mapping = aes(x = cut, y = resid))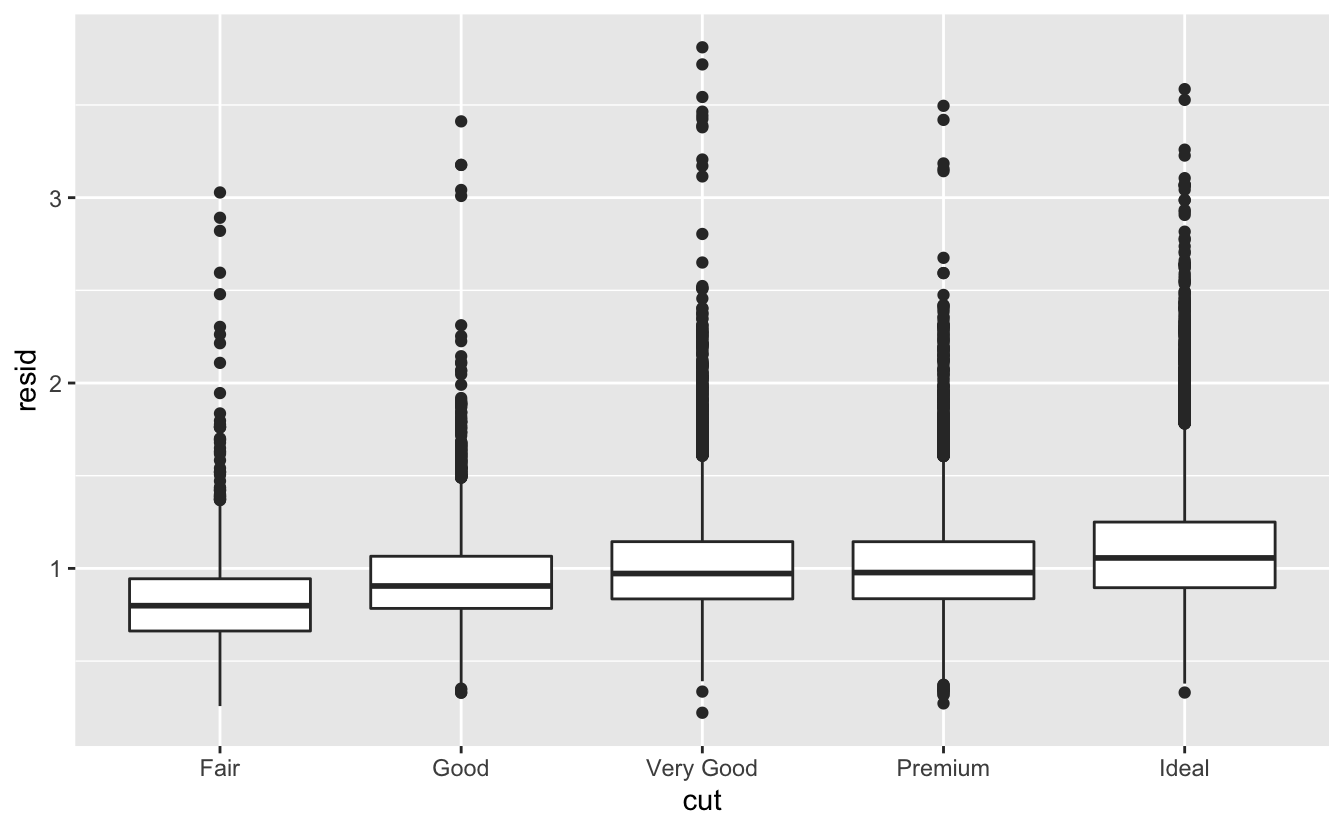
이 책에서 모델링을 다루지는 않을 것인데 데이터와 전처리와 프로그램 도구들을 가지고 있다면 모델을 이해하는 것은 쉬워지기 때문이다.
11.7 ggplot2 호출
이 장을 넘어가면 ggplot2 코드 표현을 더 간결하게 바꿀 것이다. 지금까지는 배우는 과정에 도움이 될 수 있도록 명시적인 코드를 사용하였다.
ggplot(data = faithful, mapping = aes(x = eruptions)) +
geom_freqpoly(binwidth = 0.25)일반적으로 함수의 첫 번째, 두 번째 인수는 매우 중요하므로 기억해두어야 한다. ggplot() 에서 처음 두 개의 인수는 data 와 mapping 인수이며, aes() 의 처음 두 개의 인수는 x 와 y 이다. 이 책의 나머지 부분에서는 이 이름들을 쓰지 않을 것 이다. 이렇게 하면 타이핑이 줄어들고 상용구의 양이 줄어들어 플롯 간에 다른 점을 쉽게 알 수 있다. 이는 27 에서 다루게 될 매우 중요한 프로그래밍 문제 이다.
위의 플롯을 좀 더 간결하게 작성하면 다음과 같다.
ggplot(faithful, aes(eruptions)) +
geom_freqpoly(binwidth = 0.25)때때로 데이터를 변환하는 파이프라인의 끝을 플롯으로 전환할 것이다. %>% 에서 + 로 전환되는 것을 유의하자. 이 전환이 필요하지 않으면 좋겠지만 안타깝게도 파이프가 생기기 이전에 ggplot2 가 만들어졌다.
11.8 더 배우기
ggplot2 의 메커니즘에 대해 더 알고 싶다면 ggplot2 책https://amzn.com/331924275X을 추천한다. 이 책은 최근에 업데이트되어 dplyr과 tidyr 코드가 포함되어 있으며 시각화의 모든 측면을 탐색할 수 있는 부분이 많이 포함되어 있다. 유감스럽게도 이 책은 무료로 제공되지 않지만, 학교 계정이 있다면 SpringerLink를 통해 무료로 전자 버전을 얻을 수 있다.
또 다른 유용한 자료는 윈스턴 챙(Winston Chang)의 R Graphics Cookbook 이다. 대부분의 내용은 http://www.cookbook-r.com/Graphs/에서 이용 가능하다.
또한, 안토니 언윈(Antony Unwin)의 Graphical Data Analysis with R 을 추천한다. 이 책은 이 장에서 다룬 내용과 유사하지만 더 깊이 있게 다룬다.